某客运专线T型梁受力性能研究
樊少彻 易有淼
(1.西南交通大学土木工程学院 四川成都 610031;2.中铁第四勘察设计院集团有限公司 湖北武汉 430063)
1 引言
某城际铁路采用双线客运专线设计,设计荷载为ZC标准活载,设计车辆行车速度200 km/h,使用寿命100年。本次工程使用的简支T梁以《通桥(2007)-2201》为蓝本设计,该蓝本适用于客货共线活载(ZKH)。为了适应客运专线活载(ZC)的需求,提高设计经济性、节约造价,对T型梁进行了优化设计。为检验设计的合理性,保证工程用梁的安全,抽取两片梁按《预应力混凝土铁路桥简支梁静载弯曲试验方法及评定标准》进行静载弯曲试验。
2 试验梁概况
本次试验梁为某客运专线工程用梁。两片梁的编号分别为32ZZ0174(直线中梁)和32QZ0483(曲线中梁)。当梁体混凝土抗压强度达到30 MPa时进行初张拉,达到59.8 MPa时进行终张拉,简支梁在初张拉和终张拉过程中均未出现滑丝和断丝现象[1]。两片简支T梁长32.6 m,跨度为32 m,端部和跨中截面形式相同,如图1所示。试验时两片梁均未铺设防水层,梁体预制资料见表1。
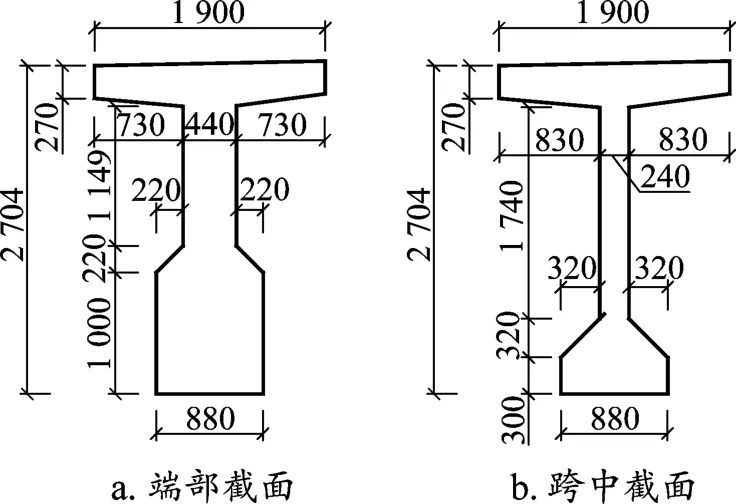
图1 试验梁截面形式(单位:mm)
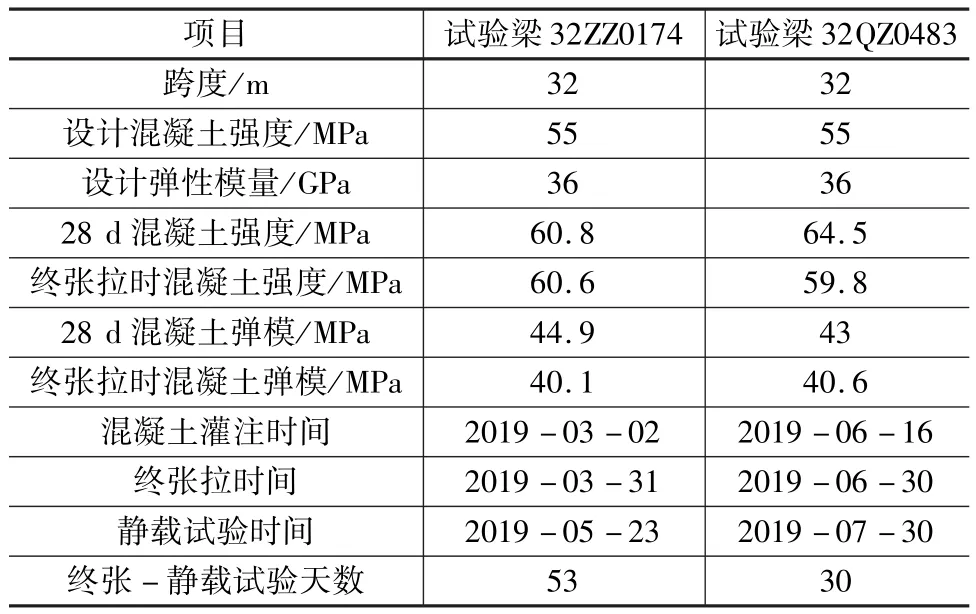
表1 试验梁基本数据
3 试验设计
3.1 试验布置
本次简支T梁静载弯曲试验的设计依据《预应力混凝土铁路桥简支梁静载弯曲试验方法及评定标准》等效集中荷载采用5点加载[2-3],各荷载纵向间距为4 m,布置如图2所示。

图2 试验梁加载布置(单位:mm)
3.2 试验步骤
(1)试验梁移入试验台座后,在梁顶画出腹板中心线,从梁体跨中沿内端每隔4 m画出5个加载点的位置,并在每一加载点下铺设垫层及垫板。在每一加载点处移入千斤顶,千斤顶底座中心用钢板垫实,梁跨中中线与中间加力架及千斤顶中心线相重合。
(2)加载前用10倍放大镜在梁体跨中两侧1/2跨中范围内的下缘和梁底面进行外观检查,对初始裂纹,包括表面收缩裂纹和表面损伤裂纹及局部缺陷用蓝色铅笔描出。
(3)试验梁的加载分两个循环进行[4-6],各级加载时间见表2。
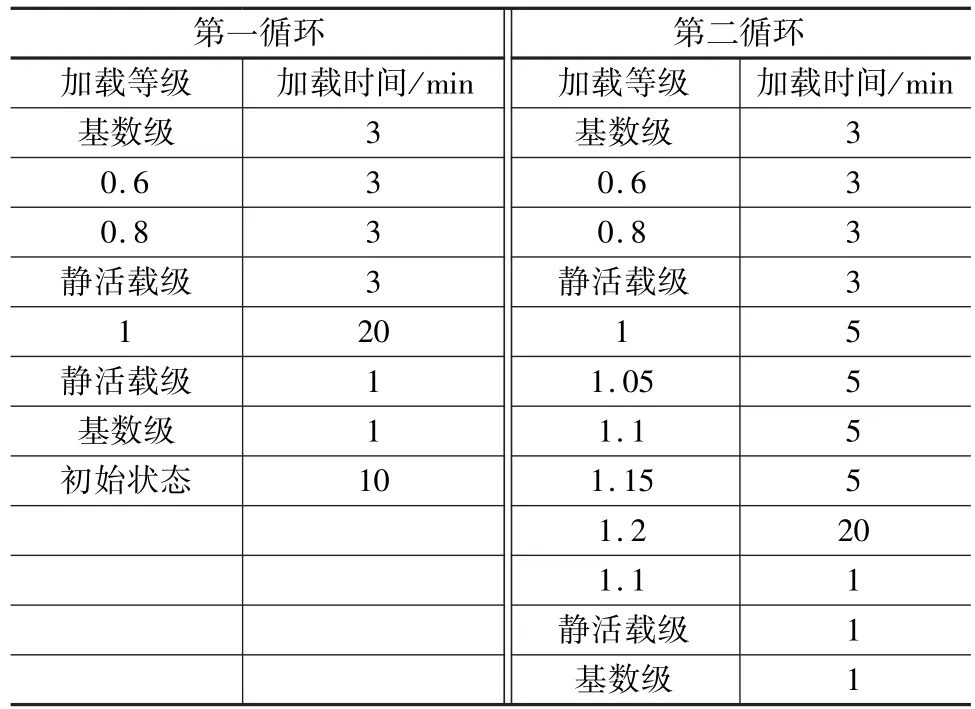
表2 各级加载时间
(4)每级加载后仔细检查梁体下缘和梁底有无裂缝出现。如出现裂缝或初始裂缝延伸,用红铅笔标注,并注明荷载等级,量测裂缝宽度。每级加载后测量梁体跨中和各支座中心截面的两侧竖向位移,以同一截面的两侧平均值作为相应截面的竖向位移量或支点沉降量。跨中截面的竖向位移量减去支点沉降影响量,即为该级荷载下的实测挠度值。
3.3 加载值计算
计算各加载级下的跨中弯矩和荷载值根据《预应力混凝土铁路桥简支梁静载弯曲试验方法及评定标准》中规定,按公式(1)~(3)计算。
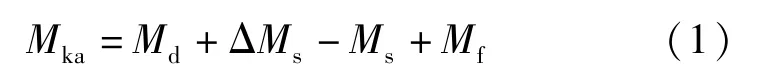
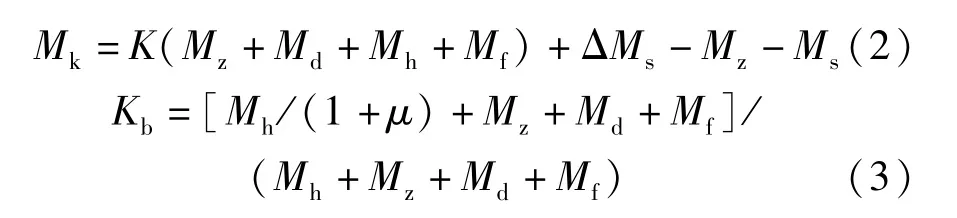
式中,Mka为基数级下的跨中弯矩(kN·m);Mk为各加载级下的跨中弯矩(kN·m);Kb为静活载级下的荷载等级;Md为二期恒载下的跨中弯矩(kN·m);ΔMs为未完成的预应力损失补偿弯矩(kN·m);Ms为加载设备对跨中的弯矩(kN·m);Mf为防水层对跨中的弯矩(kN·m);Mz为梁体质量对跨中的弯矩(kN·m);Mh为活载对跨中的弯矩(kN·m);1 +μ为动力系数。计算得出各级加载值见表3。
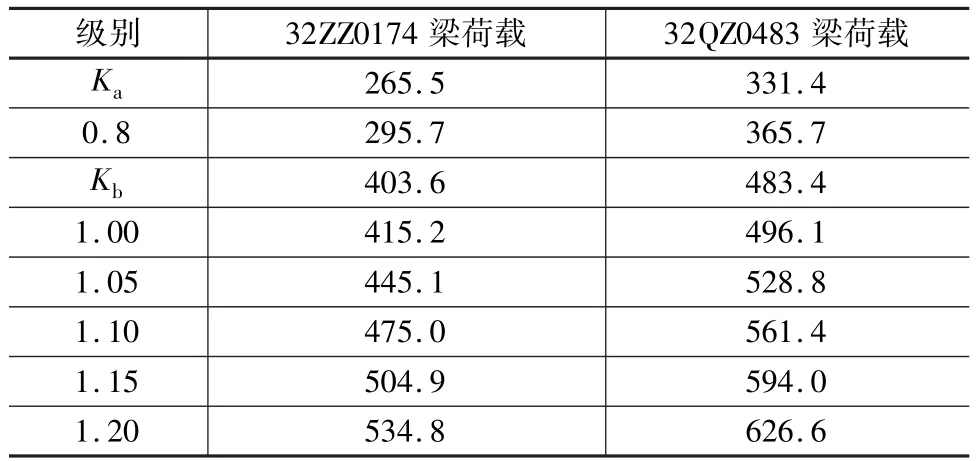
表3 试验梁各加载级荷载 kN
4 有限元模型构建与分析
4.1 模型建立
采用有限元软件Midas建立试验梁空间有限元模型,采用梁单元模拟,支座采用一般支承[7-8]。全桥共117个节点,116个单元,单元划分见图3。
图3 试验梁单元划分
4.2 模型仿真结果
(1)应力分布
在第二循环最大加载等级1.2(626.6 kN),试验梁的应力分布如图4所示。最大应力为17.266 MPa。

图4 最大加载情况试验梁32QZ0483应力分布(单位:MPa)
基数级(Ka)、静活载级(Kb)和最大加载等级下试验梁的应力分布如图5所示。由图5可以看出,应力在4 m、8 m、12 m、24 m、28 m 处有突然减小的迹象,是由于此处截面突然变大所导致。对图5中应力分布曲线进行拟合,经试验,二次函数能取得非常好的拟合效果,拟合优度在97%以上。第二循环所有加载级的应力分布拟合方程见表4。
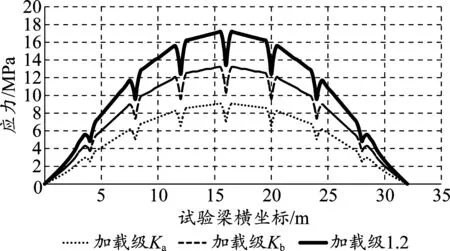
图5 各加载级试验梁应力分布(单位:MPa)
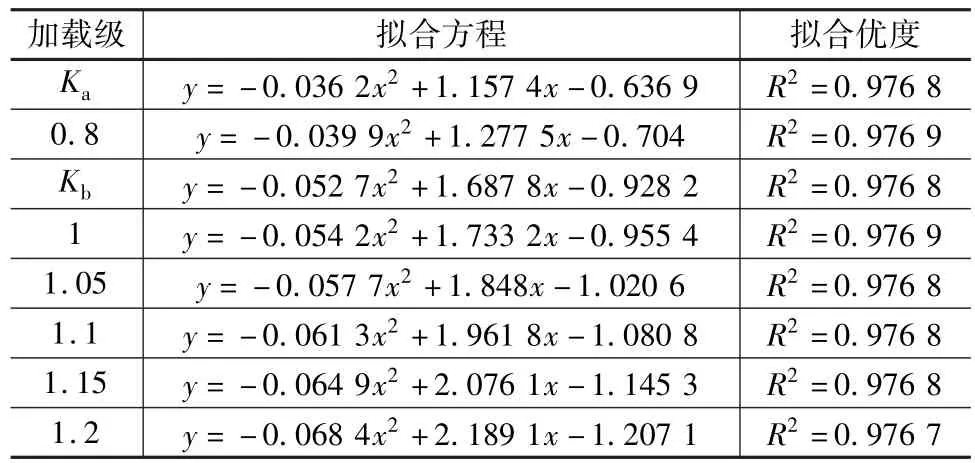
表4 试验梁各加载级应力分布拟合方程
采用归纳法和因果分析法分析可知,对于截面相同的试验梁,应力分布主要与梁长度L和加载应力P有关。
在此基础上归纳总结,基于平截面假定和线弹性理论,提出32 m预应力混凝土简支T梁应力分布方程,由此可以快速推算出该型梁在任意荷载下,梁体内某一点的应力。
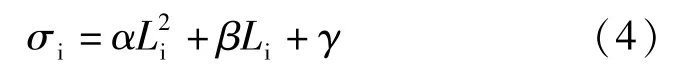
式中,σi为试验梁i点处应力(MPa);Li为i点的横坐标(m);α、β、γ为系数。

式中,P为加载力(kN);L为试验梁长度(m)。
(2)位移分布
在第二循环的基数级(Ka)、静活载级(Kb)和最大加载级(1.2)下,试验梁的挠度分布如图6所示,跨中最大挠度为29.38 mm。

图6 所有加载级试验梁挠度分布曲线
采用归纳法和因果分析法可知,对于截面相同的试验梁,挠度分布主要与梁长度L和加载力P有关。
与公式(4)推导原理相同,在此基础上归纳总结出32 m预应力混凝土简支T梁挠度分布方程

式中,Δi为试验梁i点处挠度(mm);Li为i点的横坐标(m);a、b、c为系数。

式中,P为加载力(kN);L为试验梁长度(m)。
5 试验结果与评定
5.1 试验数据分析
两片试验梁的静载挠度试验数据如图7所示。

图7 试验梁静载试验挠度曲线
图7中跨中实际挠度值是由跨中测量挠度值减去支点沉降影响量计算而得。由图7可以看出:(1)随着加载等级提高,跨中挠度逐渐增大;(2)随着加载等级提高,支座沉降变化减小,并逐渐趋于稳定;(3)在Ka~1.0阶段,两个加载循环挠度值基本一致[9-10],说明梁体处于弹性工作状态;(4)试验梁32ZZ0174扣除支座沉降值,第一加载循环最大挠度为18.43 mm,第二加载循环最大挠度为21.66 mm。试验梁32QZ0483扣除支座沉降值,第一加载循环最大挠度为21.74 mm,第二加载循环最大挠度为30.06 mm。
试验梁第二加载循环荷载值与跨中挠度的关系如图8所示。从图8可以看出,加载值与挠度基本保持线性关系(拟合优度大于99%),说明梁体处于弹性工作状态。但两条函数的斜率(0.046 2/0.05)有7%左右的差别。由结构力学原理计算出的斜率ρ=Δ/P=0.175 13L3/EI,由于两片梁长度L=32 m,考虑两片梁从张拉到试验间隔时间不同(53 d/30 d)、配筋不同、制作误差导致梁体弹性模量E有少许不同。

图8 试验梁第二加载循环荷载值与跨中挠度关系
试验梁有限元计算结果与实测结果(第二循环)对比见图9。可以看出有限元模型与实际拟合得非常好,挠度预测的误差值在1 mm以内。

图9 有限元计算结果与实测结果的对比
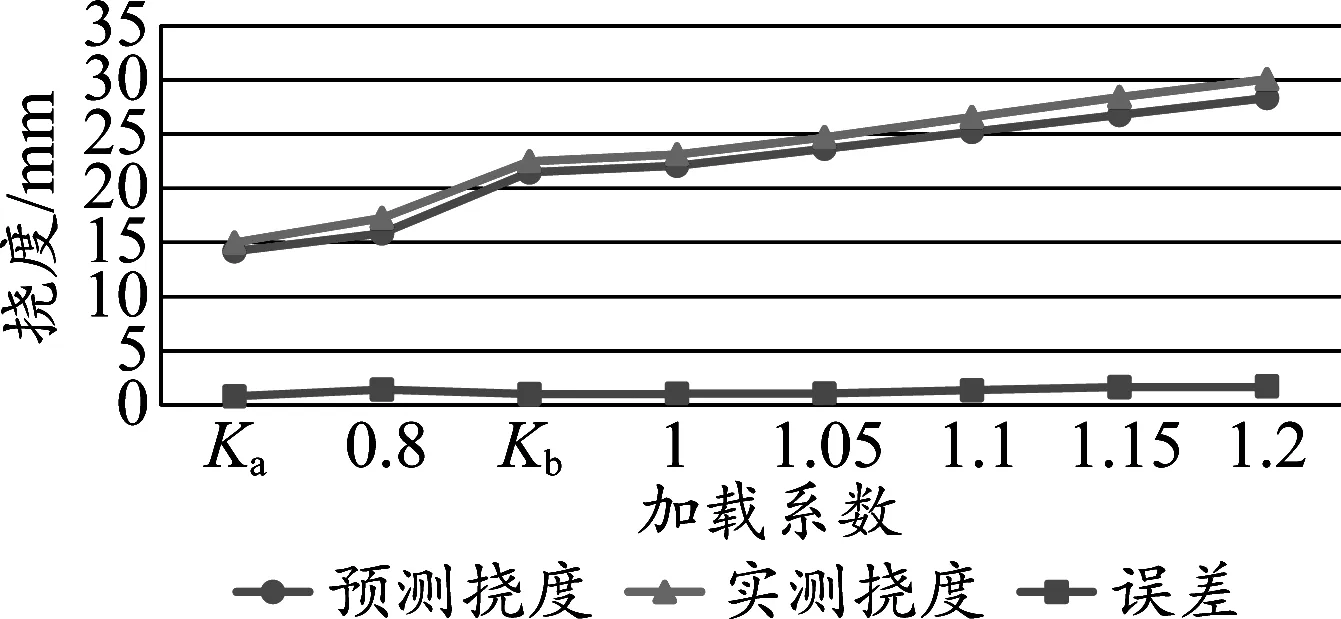
图10 预测结果与实测结果对比
5.2 结果评定
在Kf=1.2加载等级下持续20 min,两片试验梁梁体下缘底面未发现受力裂纹,两片试验梁抗裂性能均合格。实测静活载挠度值合格评定标准为f实测≤1.05f设计/φ,等效荷载加载挠度修正系数φ取1.040 9,一般以第二加载循环的挠度值作为评定依据。对于32ZZ0174梁,设计挠跨比f设计/L=1/1 399,实测挠跨比f实测/L=(fkb-fka)/L=1/5 087,满足评定标准;对于32QZ0483梁,设计挠跨比为1/3 682,实测挠跨比为1/4 265,满足评定要求。两片试验梁的刚度均满足设计要求,刚度富余量在13% ~27%之间。
6 结束语
通过对城际铁路32 m后张法预应力混凝土简支T梁的静载弯曲试验结果进行分析可得出以下结论:(1)试验T梁在静载试验结束后,其裂缝宽度、刚度、抗裂情况满足试验要求;(2)在Ka~1.0阶段,两个加载循环T梁的挠度值基本一致,表明T梁仍处于弹性阶段[11-12];(3)此类T型梁的刚度富余量在13%~27%之间;(4)基于平截面假定和线弹性理论提出了T梁应力分布预测方程和挠度预测方程,由此可以快速推算该型梁在不同荷载下某一点的应力和位移。其研究成果可为此类桥梁的设计与维护提供参考。

