管沟爆破方案FAHP优选及在役管道动力响应研究

袁旺小

(中铁十八局集团有限公司 天津 300222)

1 引言

伴随我国经济建设的高速发展，地下工程、隧道、管沟等建设量迅猛增加。由于规划、设计要求的限制，出现了大量管沟开挖工程与在役管道并行甚至交叉的现象[1]。由于爆破施工具有成本低、工期短、设备简单、适应性强等优点[2]，钻爆法仍然广泛应用于隧道、管沟等工程领域，由此管沟爆破开挖问题越来越凸显。

FAHP法在工程爆破领域应用广泛[3-6]。王丹丹[7]将FAHP应用于楼房拆除爆破的安全评价分析，通过寻找主要影响因素并加强安全管理，有效控制各个因素的危险程度，从而提高楼房拆除爆破的安全性；孙可[8]针对盾构隧道健康监测的典型传感器布置形式，提出了一类专用的模糊层次分析法综合评价模型，构建了健康监测数据的6层指标评价体系，实例证明该模型能够快速定量评价盾构隧道的健康状态并可以实现隧道运营维护的智能化管理；汪明武[9]将模糊层次分析法与实码加速遗传算法相结合应用于工程爆破领域，实例应用表明该方法可以合理确定指标权重，提高评价结果的精度和优度值的离散度。除此之外，在管沟爆破开挖方面，郑爽英[10]基于非线性动力有限元模拟方法和正交试验原理进行输气管道动力响应数值试验，按照极差分析方法确定了管道运行参数对管道应力与振速特性的影响次序；张震[11]对超浅埋地铁站通道爆破开挖邻近埋地混凝土管道的动力响应进行了研究，通过建立管道拉应力峰值和振动速度峰值的函数关系，得出由最大拉应力强度理论控制管道爆破振速的结论；彭星煜[12]采用期望反应谱作为目标谱，基于SIMQKE-GR程序模拟了地震加速度波形，建立了基于有限单元法地基梁-土弹簧模型的爆破振动作用下管道振动响应有限元模型，得出管道在爆破载荷作用下应力和位移的变化特性。但是针对管沟爆破施工对在役管道的影响却鲜有报道。

本文依据管沟爆破开挖试验、成型尺寸以及质点振动速度峰值数据，采用FAHP法优选管沟爆破方案，进行爆破荷载作用下在役管道的动力响应研究。

2 工程概况

新建铁路福州至平潭段鼓山隧道位于福州市境内，其中管沟爆破开挖处矿物组成以方解石为主，同时含有白云石、菱铁矿、石英、长石、云母等矿物质，岩石的普氏系数为6～15。管沟爆破开挖尺寸为沟底宽2.8 m，沟深3 m，并且要求管沟顺直，沟壁和沟底平整，无沟坎阶梯，无锐器物，沟内无塌方、无杂物。

邻近在役管道进行爆破工程时，要求垂直方向质点振动速度峰值应控制在10 cm/s范围内。根据工程经验以及爆破漏斗试验，初步确定3种管沟爆破开挖方案，如表1所示。此次爆破试验统一使用2号岩石乳化炸药，进行逐孔起爆网路连接，孔外采用3段毫秒导爆管雷管，延期时间为50 ms；孔内采用10段毫秒导爆管雷管，延期时间为380 ms。

表1 管沟爆破方案及参数

3 管沟爆破方案FAHP优选

3.1 建立层次结构模型

管沟爆破开挖层次结构模型以爆破方案为目标层，以少指标、全信息、考虑定性因素和定量因素为原则，进行准则层和指标层的确定，如图1所示。

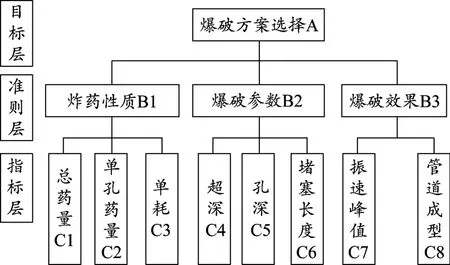
图1 爆破方案优化层次结构模型

3.2 判断矩阵及权重计算

在层次结构模型基础上，依据 T.L.Saaty教授[13]提出的1～9及其倒数标度法，将指标层两因素之间的比值构成判断矩阵，具体见表2。

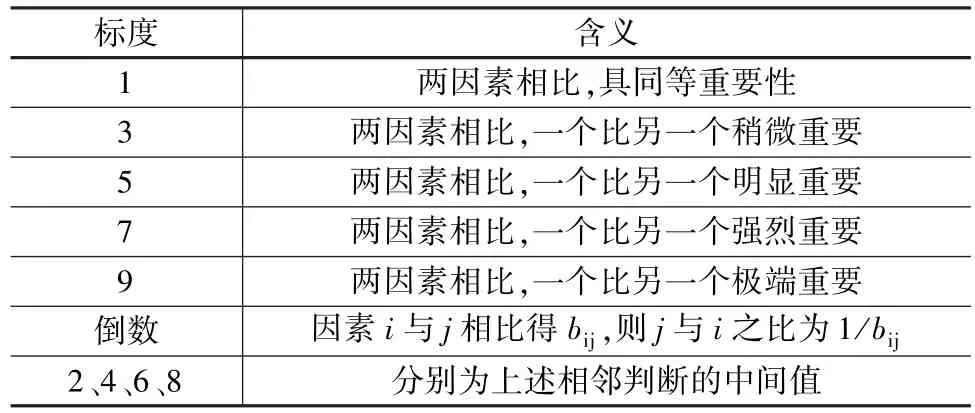
表2 判断矩阵标度值

根据判断矩阵，进行因素权重计算，步骤如下:

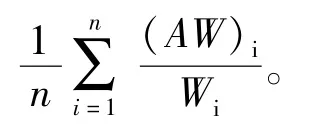
(5)为防止判断矩阵偏离一致性以致影响最终决策，需要对λmax进行一致性检验。

计算一致性比率CR:

式中，CI为一致性指标，CI＝ (λmax-n)/(n-1)；RI为平均一致性指标，按表3选取。

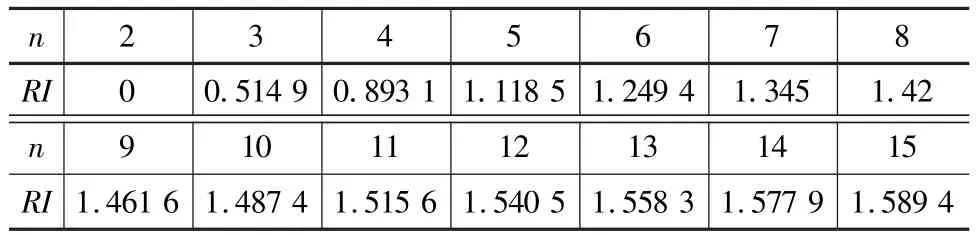
表3 平均一致性指标RI值

(6)判断矩阵满足一致性的判定标准为:CR＜0.1。否则重新调整判断矩阵因素标度值，直到满足一致性要求为止。

根据以上步骤，确定层次判断矩阵，计算权重，并进行一致性检验，结果见表4～表7。指标层各因素的总权重见表8。

表4 A-B判断矩阵、权重及一致性检验

表5 B1-C判断矩阵、权重及一致性检验

表6 B2-C判断矩阵、权重及一致性检验

表7 B3-C判断矩阵、权重及一致性检验

表8 指标总权重

3.3 确定指标隶属度

管沟爆破开挖试验过程中，采用TC-4850测振仪在距离爆源10 m处布点测试，收集垂直方向质点振动速度峰值，如图2～图4所示。在管沟爆破开挖试验结束后，立即对管沟的成型尺寸进行测量，具体指标及评价见表9。

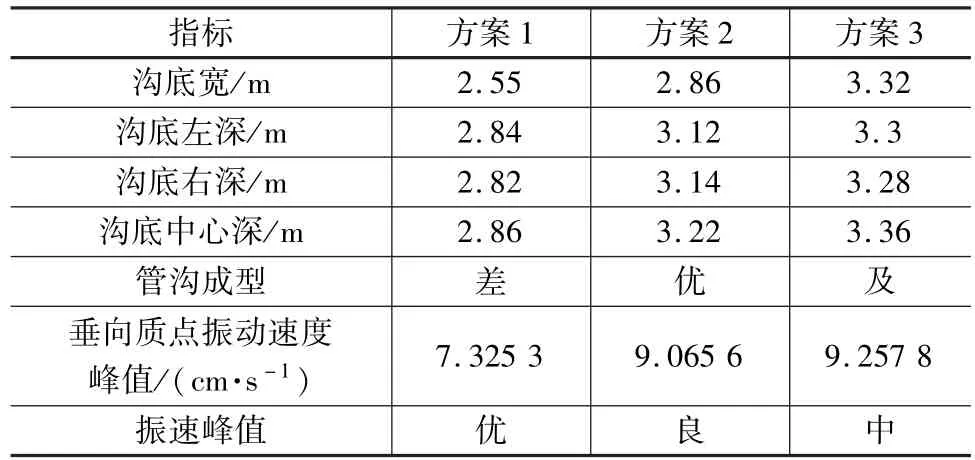
表9 管沟成型尺寸及质点振速峰值

图2 方案1爆破质点振动速度

图3 方案2爆破质点振动速度

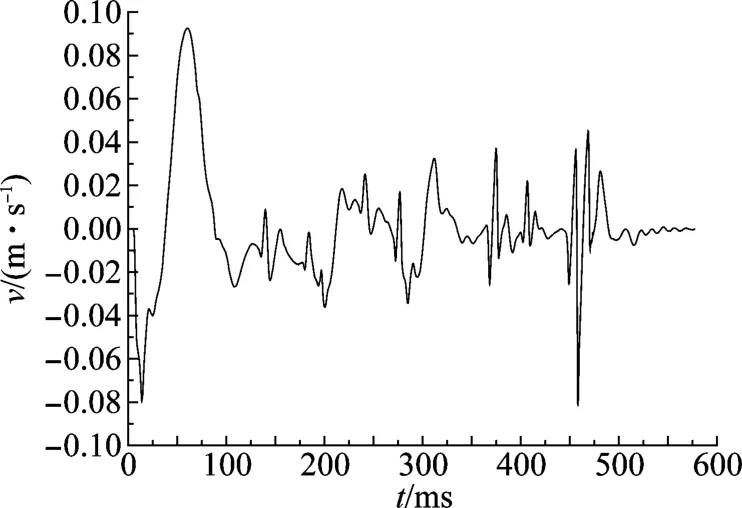
图4 方案3爆破质点振动速度

根据模糊数学理论，隶属度的确定需要考虑指标的特性。

对于定性指标，按照5级标准赋值:当为“优”时，赋值为 0.95；当为“良”时，赋值为 0.75；当为“中”时，赋值为0.55；当为“及”时，赋值为 0.35；当为“差”时，赋值为0.15。

对于定量指标，规定指标数值越大越好，为正指标，反之为负指标。利用rij＝xij/ximax计算正指标隶属度，利用rij＝1-xij/ximax计算负指标隶属度。由此可得模糊评价矩阵为:

3.4 FAHP方案优选

根据指标总权重以及模糊评价矩阵，利用加权平均模型进行计算:

根据最大隶属度原则，确定方案2为管沟爆破开挖的最优方案。

4 在役管道爆破动力响应研究

4.1 数值模型建立

采用LS-DYNA数值模拟软件，应用ALE算法，采用扫掠划分网格方式，根据在役管道的尺寸进行实际比例建模。为了简化计算，将模型尺寸设置为14 m×9 m×4 m，如图5所示。由于简化了数值模型，因此需要在底面及四周施加固定约束以及无反射边界条件。为分析在役管道动力响应的极限情况，在数值模型建立过程中，只考虑与管道相距10 m的情况，且爆破参数依据FAHP的最优方案选取。

图5 数值模型

4.2 材料模型及状态方程

数值模型包含4种材料，分别为炸药材料模型、空气材料模型、管道材料模型和岩体材料模型。炸药材料模型采用HIGH-EXPLOSIVE-BURN且定义JWL状态方程；空气模型采用NULL材料，且应用LINERPOLYNOMIAL状态方程描述；管道材料模型采用JOHNSON-COOK且定义Gruneisen方程；采用PLASTIC-KINEMATIC作为岩体材料模型，见表10。

表10 材料模型及状态方程参数

4.3 在役管道应力分析

在役管道X、Y、Z方向的应力云图见图6。

由图6可知，在役管道X方向所受的高应力状态比较集中，主要位于管道的侧壁位置处，最大值为2.33 MPa，而且管道的顶部及底部所受的应力影响也不可忽视；相比于X方向，Y方向所受应力有所减小，但仍然位于管道的侧壁处；Z方向所受应力比较均匀，对在役管道影响较小。

4.4 在役管道应变分析

在役管道X、Y、Z方向的应变云图见图7。由图7可知，在役管道X方向所受应变的最大值为8.19×105，且大应变分布区域较广，主要出现在管道的侧壁位置处；相比于X方向，Y方向所受大应变的区域范围减小，但管道顶部及底部范围的最值不降反升，而且比较集中；Z方向所受应变比较均匀，对在役管道影响较小。

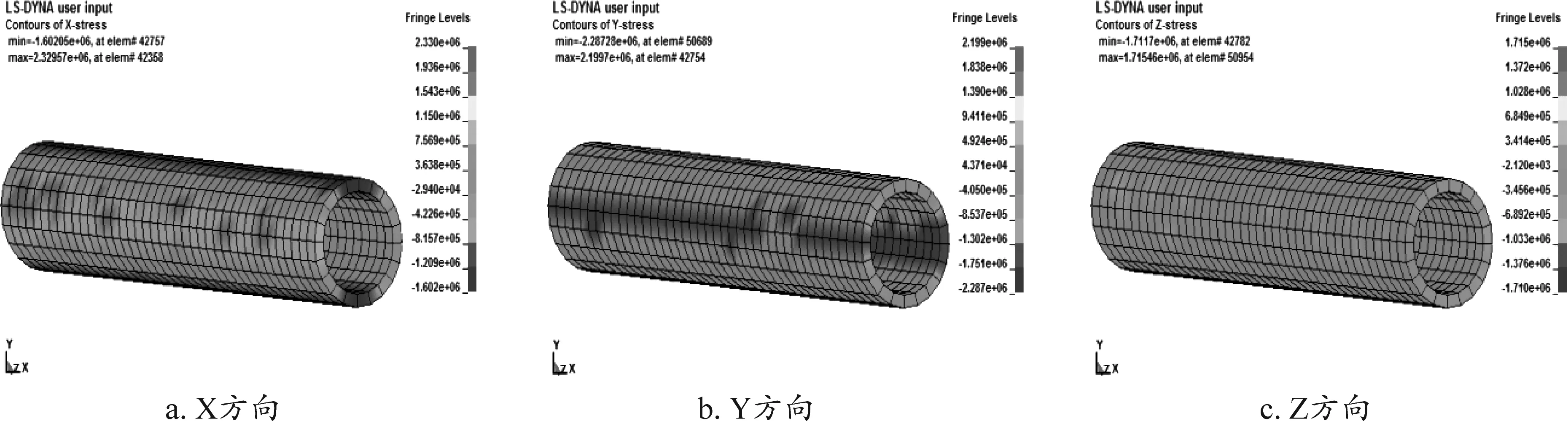
图6 在役管道应力云图

图7 在役管道应变云图

5 结论

(1)通过建立层次结构模型，构造判断矩阵，进行权重计算，按照最大隶属度原则进行管沟爆破开挖方案的优选，可以为类似管沟爆破工程提供参考。

(2)采用FAHP法确定方案2为管沟爆破开挖的最优方案，其管沟成型尺寸最接近标准尺寸，而且其垂向质点振速峰值为9.065 6 cm/s。

(3)通过数值模拟分析爆破开挖对在役管道的动力响应，结果表明，在役管道X方向所受的影响最为显著，并且高应力及大应变主要集中在管道的侧壁位置处，管道的顶部及底部也应该加强防护。