考虑基础振动与惯量不确定的机械臂力位混合控制
王佳松,郭宇飞,王志刚,郝志强
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2.武汉科技大学机器人与智能系统研究院,湖北 武汉,430081)
机械臂在制造业的自动化生产中发挥了重要作用,目前一般工业界的机械臂大多被使用在位置模式下[1-3],当考虑到与环境进行交互作用的情况,比如研磨[4]、抛光[5-6]或边缘去毛刺[4]等,机械臂在遵循与表面相切且规定运动轨迹的同时还需要施加垂直于给定表面的力,因此机械臂的力位混合控制研究应运而生。在机械臂的力位混合控制研究中,有的将接触表面建模为刚性[7],有的则将其建模为弹性[8];有的假设机器人将移动到物体表面,有的则使机器人失去与物体表面的接触[9]。为了处理不确定的机器人参数或未知环境,研究人员已经开始在力位混合控制问题中使用视觉识别[10]、反步控制[11]、神经网络[12]、模糊逻辑与常规滑膜控制[13]、克服高斯白噪声[14]以及针对运动或动态不确定性的鲁棒控制[15-17]和自适应控制[18-24]等。另外,Peng等[25]采用一种基于观测器的力位混合跟踪控制,用于参数不确定和外部扰动的机器人系统;Singh等[26]开发了一种自适应补偿器,在不需要扰动界先验信息的情况下,消除近似误差和外部扰动或未建模动力学等扰动项的影响;Fanaei等[27]设计了一种鲁棒的自适应神经模糊补偿器和在线估计器,补偿器用来补偿末端执行器和物体表面之间的摩擦力,估计器用来确定物体表面的刚度系数,更加准确地计算控制所需要的力;Kumar等[8]将机器人动力学分解为力、位置和冗余联合子空间来设计控制器;Hsu等[28]设计的控制体系结构由外环命令发生器和内环自适应模糊力位混合控制器组成。可见,对于机器人力位混合控制问题的解决方案,大多还是集中于将常规控制方案与智能技术或辅助控制相集成。
目前,力位混合控制的研究大多还没有考虑机械臂安装基础的振动,但安装存在基础随机振动的机械臂在机器人领域已经成为了研究热点。Lin课题组[29-31]研究了一类安装在起重机台架等柔性部件上的机械臂,将安装基础振动简化为线性弹簧阻尼,基于混合控制策略实现机械臂末端的精确定位与安装基础柔性振动的有效抑制,其中安装基础振动主要考虑来自于自身结构的柔性特性,而实际工况下机械臂受到的基础振动则主要来自系统的外部激励。Kiguchi等[32]提出了一种模糊矢量方法,该方法使控制器能够处理力传感器信号,例如来自噪声或由作业工具引起的未知振动信号,以确定未知物体约束面的方向。研究人员选择不同的方法来控制系统的振动幅度,但是主动振动控制也存在一些缺点,例如需要额外的执行器和传感器以及消耗更多的能量。
本文以常见的两连杆机械臂为研究对象,针对机械臂与环境接触碰撞过程中受到基础振动和负载惯量不确定性的影响,将机械臂末端的力控制和位置控制解耦到正交空间下,采用比例-积分加接触力前馈控制方法和一种基于隐式李雅普诺夫(Lyapunov)函数的控制算法分别进行力控制和位置控制,设计一种用于连续时变反馈机械臂位置控制的力位混合控制器;并在基础振动下与传统的机械臂力位混合控制器性能进行仿真对比,同时对该力位混合控制器在负载惯量不确定情况下的性能进行仿真计算,以期为机械臂在恶劣工况下的力位混合控制提供参考。
1 受约束机械臂动力学模型
机械臂的简化模型如图1所示。图1中,XOY为笛卡尔坐标系;第一节机械臂的质量为m1、旋转角度为q1、杆长为l1;第二节机械臂的质量为m2、旋转角度为q2、杆长为l2;xs为环境中接触表面的恒定位置;x为机械臂实际位移;yr为机械臂与坐标系的相对位移。
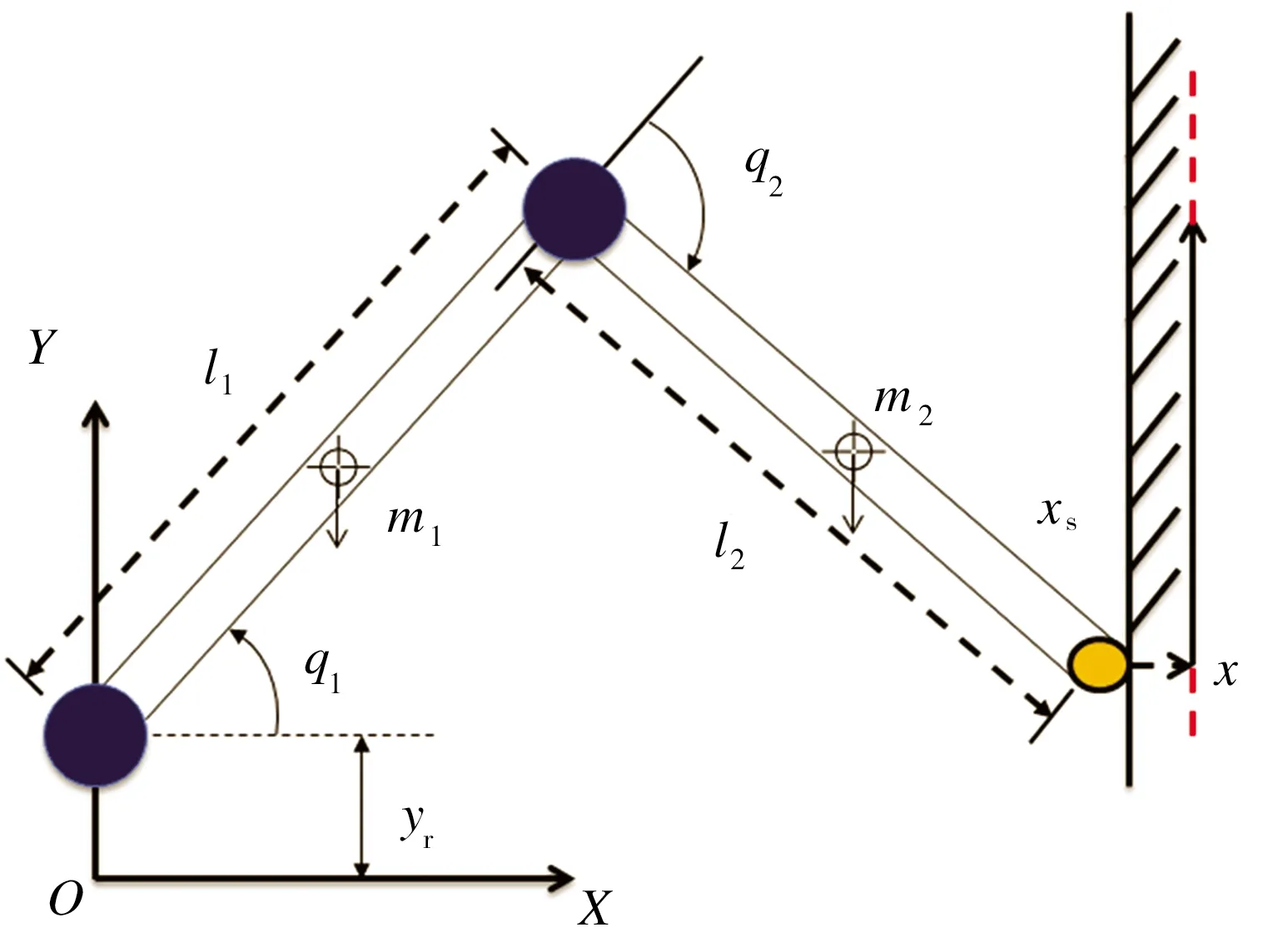
图1 机械臂的简化模型
选取q=[q1,q2]T为广义坐标,考虑末端运动受环境约束的两关节机械臂系统,则机械臂的动力学方程为:
(1)
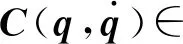
(2)
(3)
(4)
(5)
机械臂的动力学方程具有以下几个性质:
性质1 惯量矩阵M(q)为正定对称矩阵,且上下有界,即对于任意一个向量z,有:
wz2≤‖zTM(q)z‖≤Wz2
(6)
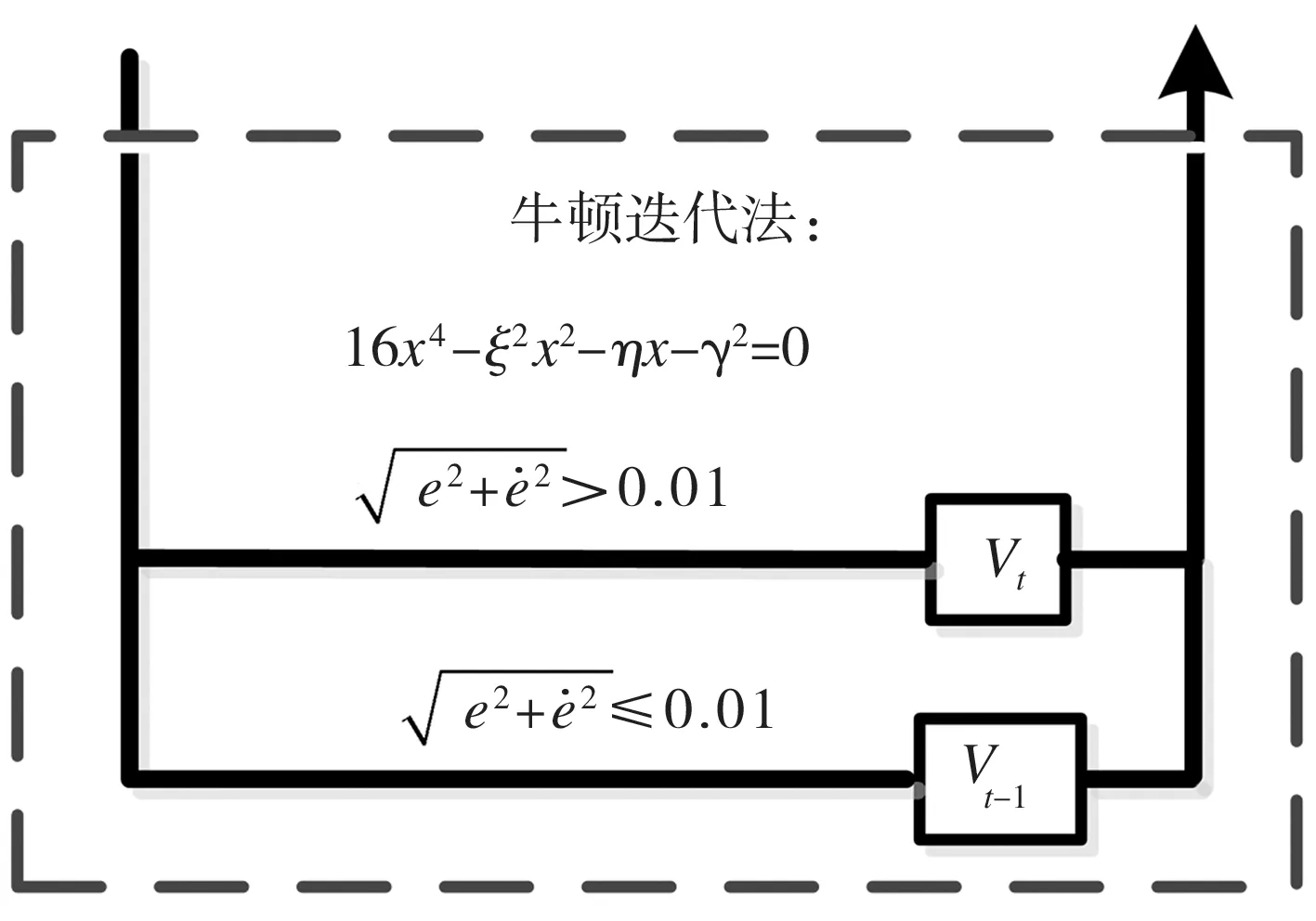
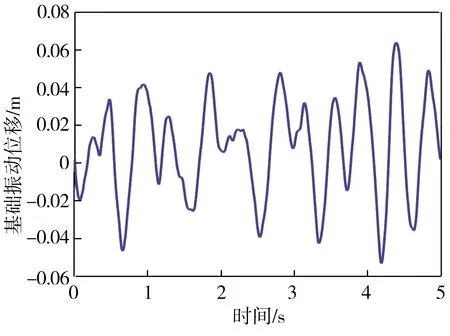
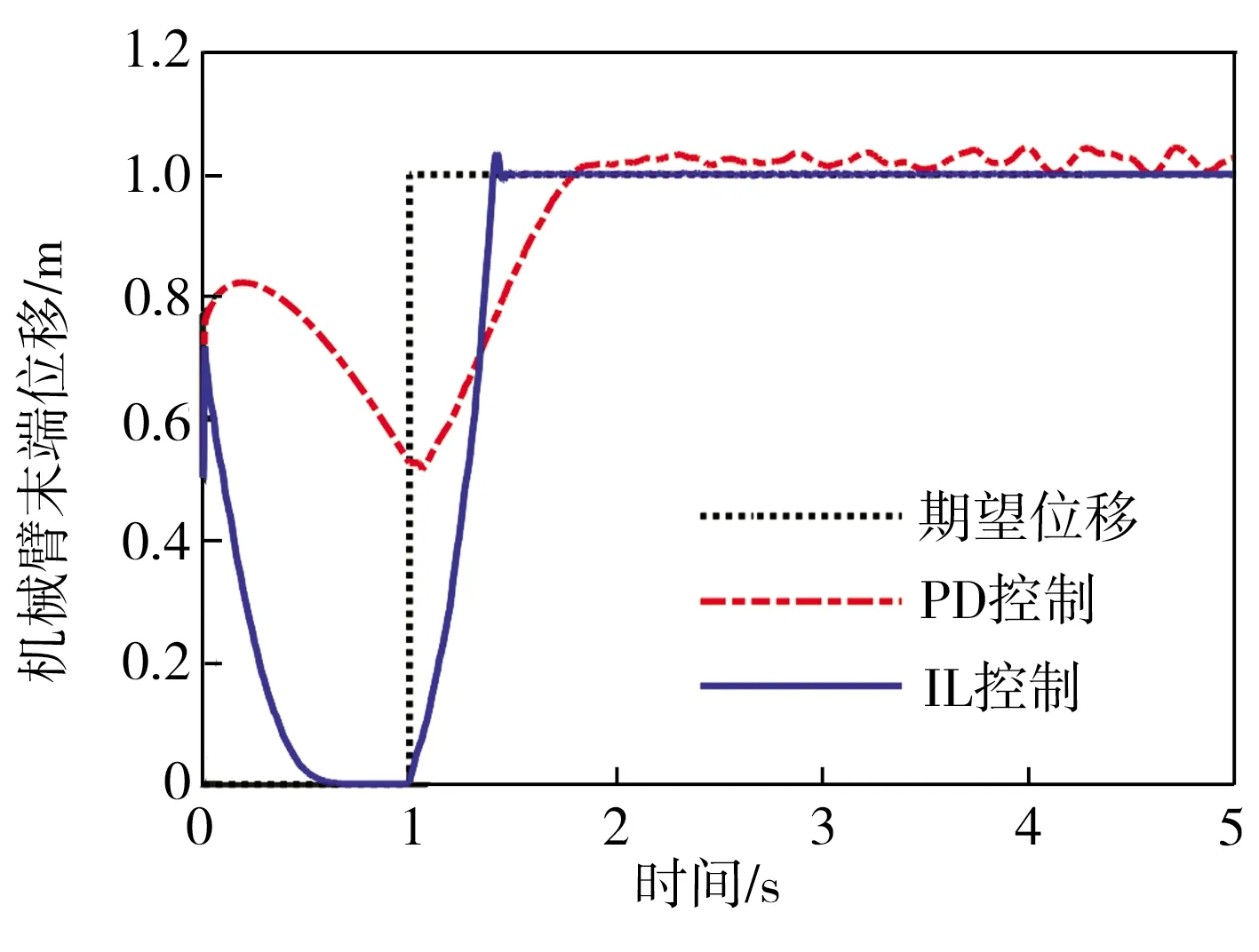
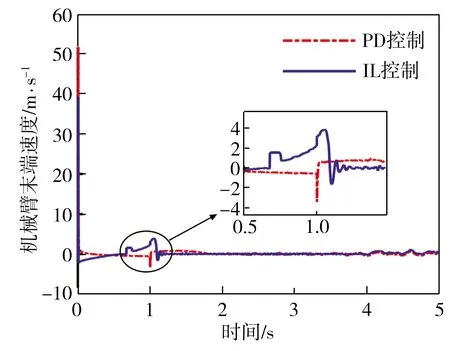
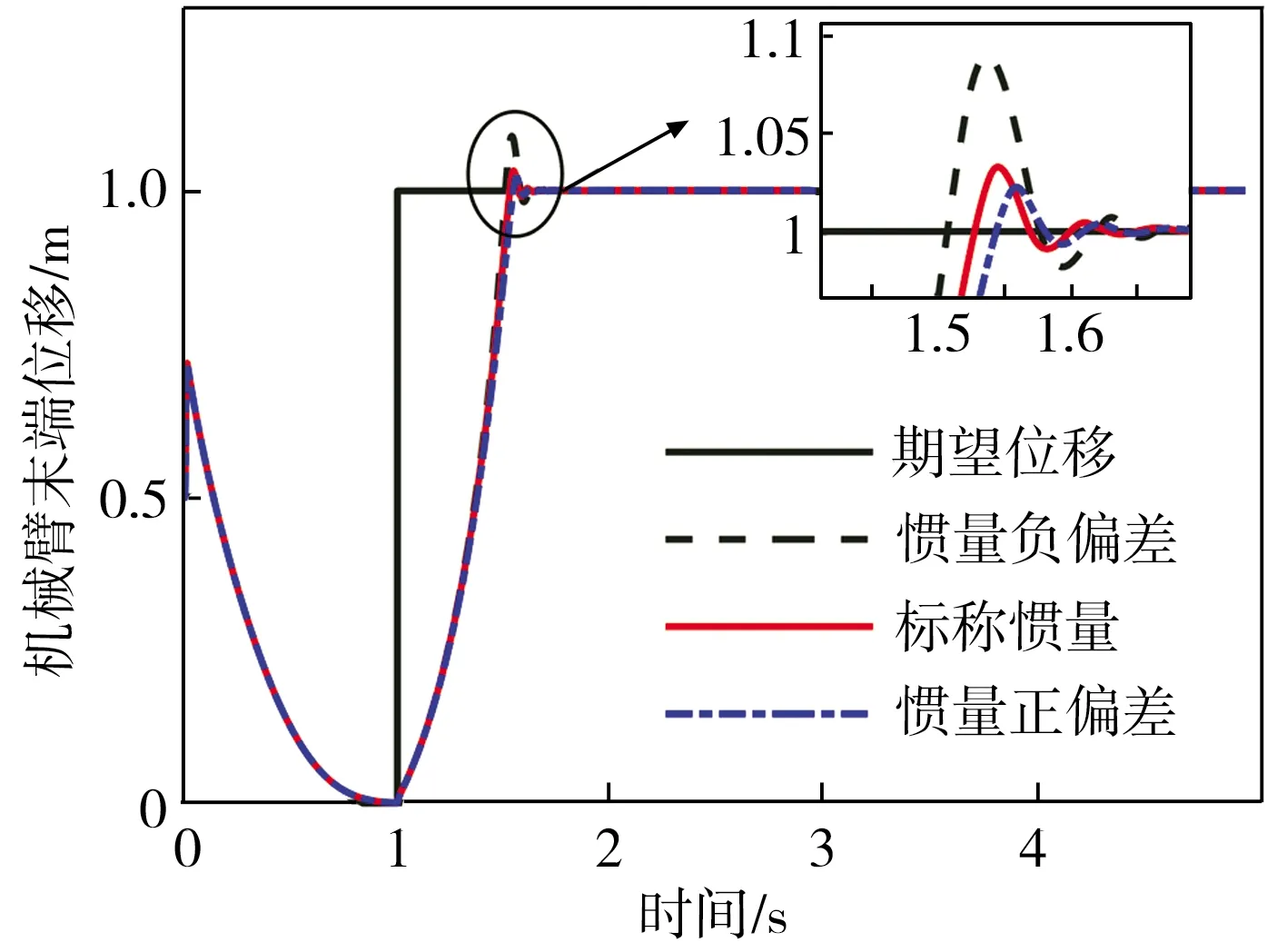
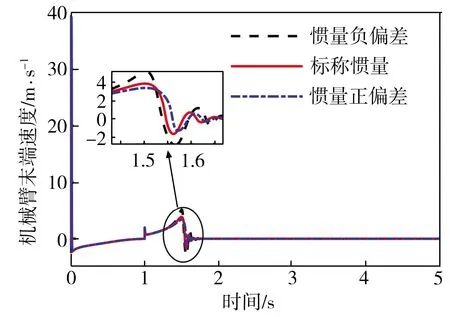
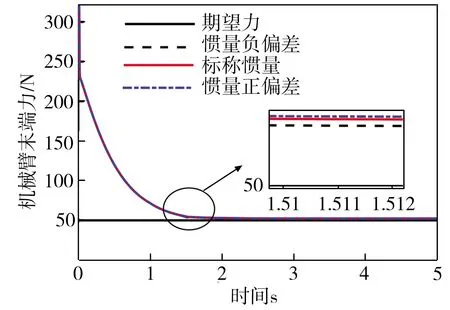
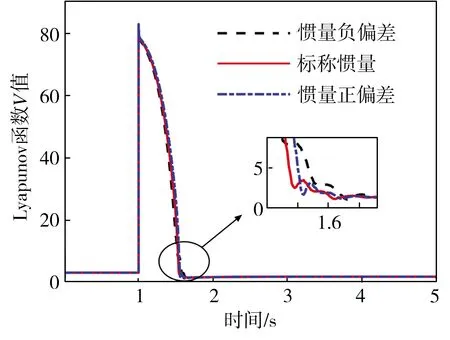
式中:0 性质2 存在常数H0>0,使得机械臂广义外部扰动力向量满足: ‖H‖≤H0 (7) 性质3 存在常数U0>0,使得机械臂广义控制力向量满足: ‖U‖≤U0 (8) 性质4 存在常数c0>0,使得机械臂向心力/科氏力向量满足: (9) 性质5 存在常数g0>0,使得机械臂重力向量满足: ‖G(q)‖≤g0 (10) 连续时变反馈力位混合控制回路如图2所示。在图2中,有两个闭环控制,其中上面一个为位置闭环控制,下面一个为力闭环控制,通过雅可比矩阵与机械臂正、逆运动学完成力和位置在笛卡尔空间与关节空间中坐标的相互转换,故在笛卡尔坐标系下机械臂控制力(矩)为: (11) 式中,Δx为机械臂末端实际轨迹与期望轨迹的误差, m;kp为位置控制系统中的比例增益系数;kd为位置控制系统中的微分增益系数;ΔF为机械臂末端实际力与期望力的误差, N;KFp为力控制系统中的比例增益系数;KFi为力控制系统中的积分增益系数;Fd为机械臂末端期望力, N。 图2 连续时变反馈力位混合控制回路 2.2.1 位置控制器设计 位置控制是基于一种给定隐式Lyapunov函数的增益时变反馈控制,通过给定某一时刻的系统状态变量与各状态变量的期望值,便可根据二者误差采用牛顿迭代法求解出该时刻Lyapunov函数的值(简称V值),当V值有唯一解时,即可求出该时刻增益系数的反馈值,完成位置控制器的设计。 通过计算力矩法引入变量τ′和H′,并定义: (12) 将式(12)代入式(1),消去非线性项后,得: (13) 由于M(q)的可逆性,进一步化简上式,得: (14) 定义: (15) 式中,qd为广义坐标的期望轨迹,是一个连续且二次可微的时变函数。 将式(15)代入式(14),得到位移误差方程: (16) 式中,e为位移误差,e=qd-q。 如果不考虑基础振动的影响,即在H′=0的情况下,用经典比例-微分控制(简称PD控制)方法便可以确定定常PD增益系数kd与kp的值。 2.2.2 基于隐式Lyapunov函数的控制律 如果考虑基础振动的影响,即当H′≠0的情况下,上述定常增益系数的PD控制器不再适用,重新选择kd与kp为: (17) 式中,u0为一个正实数;kd与kp满足关系式: (18) (19) 定义辅助控制变量u为误差系统的控制力向量,其表达式为: (20) 由式(17)、式(20)与柯西定理可得: (21) 由式(18)、式(19)进一步化简式(21)可得: (22) 由式(21)和式 (22)可得: ‖u‖≤u0 (23) 根据柯西定理,有: (24) 又定义: (25) 式中,η、ξ与γ之间满足关系式: ξ2+γ2>0,|η|≤|ξγ| (26) 将式(25)与式(17)代入式(19),可得: 16x4-ξ2x2-ηx-γ2=0 (27) (28) 将式(16)代入式(28),化简得: (29) 又因为: (30) 将式(30)与式(18)代入式(29),得: (31) 根据柯西定理求式(31)等号右边第二项的上界,得: (32) 根据柯西定理与式(18)、式(19),得: (33) 根据式(32)和式(33),可得: (34) 根据性质1、性质2与公式 (12)中的第2个等式,可得: (35) 根据式(34)和式(35),可得: (36) 定义: (37) 由柯西定理可得: (38) 将式(18)代入式(38),得: (39) 再将式(39)代入式(37),得: (40) 将式(36)、式(17)中的第一个等式、式(40)代入式(31),得: (41) (42) (43) 由性质1、性质4、 性质5与式(23)和式(43)可知: (44) 2.2.3 控制回路与计算流程 图3 连续时变反馈控制器结构示意图 力控制采用传统的比例-积分控制(简称PI控制)和接触力前馈控制。根据胡克(Hooke)定律,在接触材料中的环境测量力为: (45) 式中,Ke为环境刚度。 通过将实时测量机械臂末端受到的力(Fm)与期望力(Fd)进行比较,从而实现力的闭环控制。 图4 机械臂的基础振动位移 在机械臂的位置控制系统中,所选控制器将机械臂系统末端位移与期望位移的差作为反馈,首先使用PD控制器来进行驱动,通过控制变量的方法,得到调试控制效果较好时PD控制器的比例增益值与微分增益值分别为:Kp=-200、Kd=10;再使用基于隐式Lyapunov函数控制的连续时变反馈控制器(简称IL控制器)进行驱动。IL控制器与传统PD控制器的跟踪轨迹、速度对比分别如图5、图6所示。从图5和图6中可以看出,在位置控制系统中,无论是位移还是速度,IL控制器在控制精度和响应时间上较PD控制器均有明显提升。 图5 IL控制器与传统PD控制器的跟踪轨迹对比 图6 IL控制器与传统PD控制器的速度对比 在机械臂的力控制系统中,IL控制器与传统PD控制器在力控制方案中的控制器类型相同,初始参数值与位置控制方案也保持一致。选择PI控制器和接触力前馈控制来进行期望力的跟踪控制,该控制器将机械臂系统末端力与期望力的差作为反馈,选择PI控制器的比例增益值与积分增益值分别为:KFp=20,KFi=10。IL控制器与传统PD控制器力跟踪对比及IL控制器的Lyapunov函数V值计算结果分别如图7、图8所示。从图7中可以看出,随着位置控制系统性能的提升,IL控制器比PD控制器在力控制系统中具有更快的跟踪速度。从图8中可以看出,IL控制器在出现阶跃信号后,V值由大减小,最终趋于一个稳定的极小值,避免了出现kd和kp的值趋于无穷大的情况,由此表明,IL控制器在满足计算机的允许计算位数和精度的同时,凸显了能实时计算kd和kp值的优点。 图7 IL控制器与传统PD控制器的力跟踪对比 图8 IL控制器的Lyapunov函数V值 IL控制器与传统PD控制器的位移误差对比和力误差对比分别如图9和图10所示。从图9和图10中可以看出,与传统的PD控制器相比,在基础振动的影响下,IL控制器具有快、准、稳的特点,能够更好地跟踪机械臂末端的位置和力,具有很好的跟踪效果。从图9中可以看出,在未加载阶跃信号(0~1 s)时,IL控制器能够很快地将位移误差减少到0;在出现阶跃信号(1~5 s)后,也能在比传统PD控制位移误差幅值大的情况下快速地将位移误差减少到0,并且保持稳定。从图9 图9 IL控制器与传统PD控制器的位移误差对比 图10 IL控制器与传统PD控制器的力误差对比 中还可以看出,在控制精度和曲线平滑度上,IL控制器的性能都要明显好于传统PD控制器,充分体现出IL控制器的优势。从图10中可以看出,IL控制器中位置控制所带来的系统稳定性,使得IL控制器的力跟踪误差性能比传统PD控制器的性能也有一定提升。 基于上述惯量参数为标称惯量,将机械臂惯量减少50%作为惯量负偏差,将机械臂惯量增加50%作为惯量正偏差,计算得到IL控制器的跟踪轨迹、控制速度、力跟踪及Lyapunov函数V值分别如图11、图12、图13、图14所示。计算结果表明,系统惯量越大,IL控制器需要越长的时间来驱动机械臂以跟踪上期望值,但是,无论机械臂负载惯量是否存在偏差,IL控制器都能较好地完成力位混合控制,表明该控制算法具有良好的鲁棒性。从图11中可以看出,随着负载惯量的不断增大,整个过程中机械臂末端位移波动量也随之减小,体现在IL控制器的位移跟踪幅值不断降低。从图12中可以看出,惯量负偏差下IL控制器的跟踪轨迹响应速度最快,标称惯量次之,惯量正偏差最慢。综合来看,在面对机械臂负载惯量不确定情况下,IL控制器的跟踪速度和控制精度都比较稳定,具有极强的鲁棒性。从图13中可以看出,在惯量负偏差时机械臂末端力的跟踪速度 图11 惯量不确定情况下IL控制器的跟踪轨迹 图12 惯量不确定情况下IL控制器的控制速度 图13 惯量不确定情况下IL控制器的力跟踪 图14 惯量不确定情况下IL控制器的Lyapunov函数V值 最快,标称惯量次之,惯量正偏差最慢,但是在惯量不确定情况下,IL控制器的控制精度偏差较小,控制器稳定性较强。从图14中可以看出,负载惯量不确定性对于Lyapunov函数的V值选取也有一定的影响,惯量负偏差下V值的选择速度较快,标称惯量下V值的选择速度次之,惯量正偏差下V值的选择速度最慢,并且,负载惯量越小,曲线的平滑度越好,V值选取值的波动越小。 (1)针对机械臂与环境接触碰撞过程中受到基础振动和负载惯量不确定的影响,将机械臂末端的力控制和位置控制解耦到正交空间下,采用比例-积分加接触力前馈控制方法和一种基于隐式Lyapunov函数的控制算法分别进行力控制和位置控制,设计一种用于连续时变反馈机械臂位置控制的力位混合控制器。 (2)所设计的力位混合控制器能够抑制基础振动和不确定惯量的影响,实现了基础振动与惯量不确定情况下接触力和位置的同时控制。 (3)与传统的力位混合控制器相比,所设计的力位混合控制器在控制速度、控制精度和稳定性等方面性能均有明显提升,具有良好的鲁棒性。2 控制方案和稳定性分析
2.1 连续时变反馈力位混合控制方案
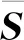
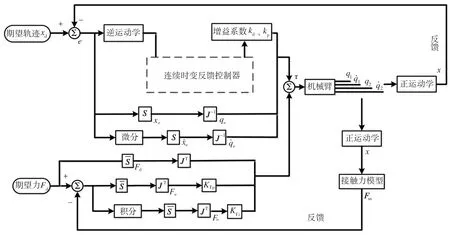
2.2 连续时变反馈位置控制方案
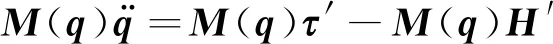
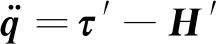
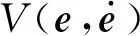
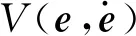
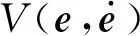
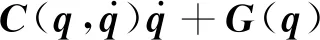
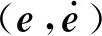
2.3 力控制方案
3 仿真结果与分析
3.1 控制器对比仿真
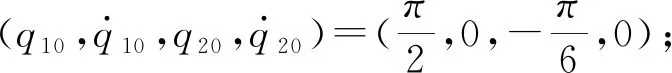
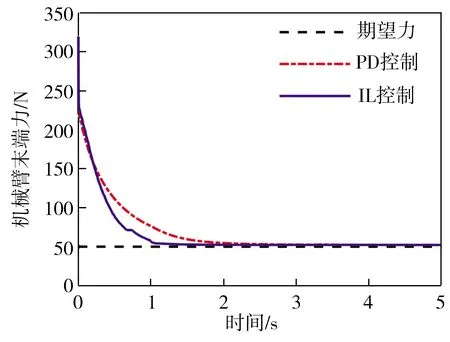
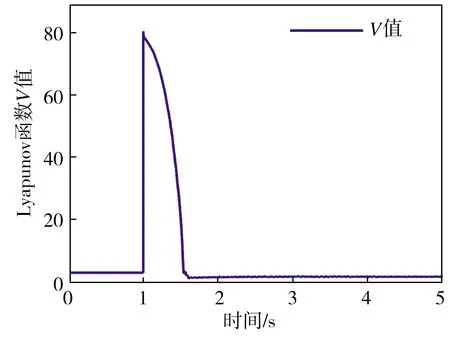
3.2 控制器误差对比仿真
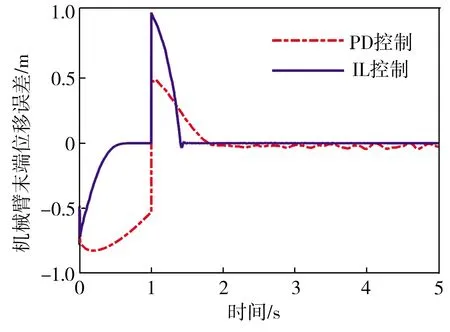
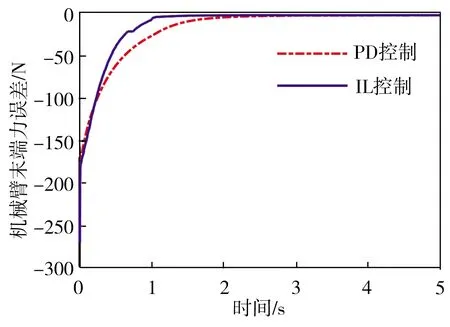
3.3 惯量不确定下IL控制器性能仿真
4 结论

