多粒度矿体模型不确定性表达与传递研究

李 江，徐江嬿

(1.湖北省自然资源厅信息中心,湖北 武汉, 430071；2. 湖北省自然资源厅地质勘查基金管理中心,湖北 武汉, 430071)

矿体三维模型是开展地质空间分析、矿产资源评价、储量计算等方面工作的数据基础和对建模区域地质情况的直观表达[1-2]。受矿体地质结构的复杂性、人类对矿体认知的不完备性及矿体采集数据的稀疏性等多方面因素影响，不确定性成为矿体三维模型的固有属性并贯穿于矿体建模过程的始终[3-5]。对矿体建模过程中的误差来源、表达方式和传递机制进行分析，建立模型的不确定性传递模型和分析方法，将极大提高其实用价值和应用程度。国内外研究人员对矿体三维模型不确定性进行了大量研究。徐华等[6]分析了矿体三维建模各环节中的不确定性问题, 建立了基于三维地质模拟各环节的误差检查机制, 并针对不确定性极为突出的断层模型, 设计了断层模型质量评价方法。Keefer[7]认为模型的不确定性来源主要包括数据的准确性和精度、数据的数量和空间分布、地质复杂性、地质解译等四个方面。英国地质调查局在DGSM项目中，采用因果关系图对三维地质模型不确定性的来源进行了分析，利用poor、ok、good三个等级相应的分析规则对模型质量不确定性进行了半定量分析[8]。Brdossy等[9]提出了不确定性区间(uncertainty intervals)、模糊集(fuzzy sets)、概率范围(probability range)、神经网络(neural networks)、混合算法(hybrid arithmetic)、模糊地质统计学(fuzzy geostatistics)等一系列描述地质不确定性的数学方法，以期采用数学方法解决模型不确定性的评估问题。史文中[10]对三维GIS的位置误差进行研究，提出了三维地理信息系统中几何特征(三维点、三维线段和三维线)误差模型。Wellmann课题组[11-12]依托建模数据的概率分布及初始地质模型，将地质空间划分成若干 Grid 或 Voxel 单元体，对层状地质体的不确定性及误差敏感度进行熵值计算，实现了地质体三维空间内的不确定性分析。尽管概率论、空间统计学、模糊数学、粗糙集等多种理论和方法被用于矿体三维模型的不确定性传递和定量分析，然而不确定性在三维矿体建模整个过程中的传播和定量描述仍然是尚未解决的难题，尤其是误差计算方法、修正机制及其实现技术等仍处于探索阶段，对矿体三维模型的不确定性表达与传递过程的研究仍需进一步提高。为此，本课题组依据矿山企业对三维模型在波动性、精确性等方面不同的特征表达需求，提出了以置信度为约束的基于语义的矿体多粒度模型建模方法，并根据信息熵理论提出了矿体三维模型的不确定性定量分析、模型误差检测与修正的技术框架和实现步骤[13]，本文在此研究基础上，针对矿体多粒度模型的不确定性，应用不确定性推理理论的可信度(Certainty Factor，CF)方法和地质统计学中的克里格算法，对矿体模型构建过程中的不确定性分布与传递过程进行分析，建立多粒度矿体模型的不确定性表达与传递模型框架,以期为矿山企业利用矿体三维模型实现勘探设计、施工计划、目标决策等应用方面提供参考。

1 矿体三维建模不确定性来源与传递过程

矿体三维模型是利用地质剖面、勘探钻孔、断层及褶皱构造等多源地质数据结合插值拟合等算法进行数学模拟的结果，是对矿区地质和矿产赋存等情况的描述和表示。在建模过程中,不确定性贯穿于地质数据的获取、整理、入库及模型计算的始终，因此矿体三维模型的建立过程也是其不确定性的传递过程。根据建模步骤，矿体三维模型的不确定性来源可归纳为：样本采集与测量误差、数据不完整性和不一致性、矿体认知不确定性、内插或外推随机不确定性以及建模算法的不确定性[14]。矿体三维建模不确定性的分布如图1所示。

图1 矿体三维模型不确定性分布

2 矿体建模不确定性算法实现

2.1 基于可信度的不确定性推理

不确定性的表达和处理是人工智能研究的重要课题之一，属于非线性复杂问题范畴，主要研究方法包括基于可信度、基于模糊和基于概率三个方面，其中，可信度(CF)方法是在确定性理论的基础上，结合概率论、非概率和非形式化推理过程提出的一种不确定性推理模型，是在不确定性的知识或现象中引入了可信度概念，使原本模糊的知识或现象变得定量化和明确化。可信度又称可信度因子或规则强度，包括证据可信度和规则可信度，取值在[-1,1]范围内，其定义一般通过概率给出，假设CF(H,E)表示当证据E出现时结论H成立的支持程度，CF(H,E)形式化定义为：

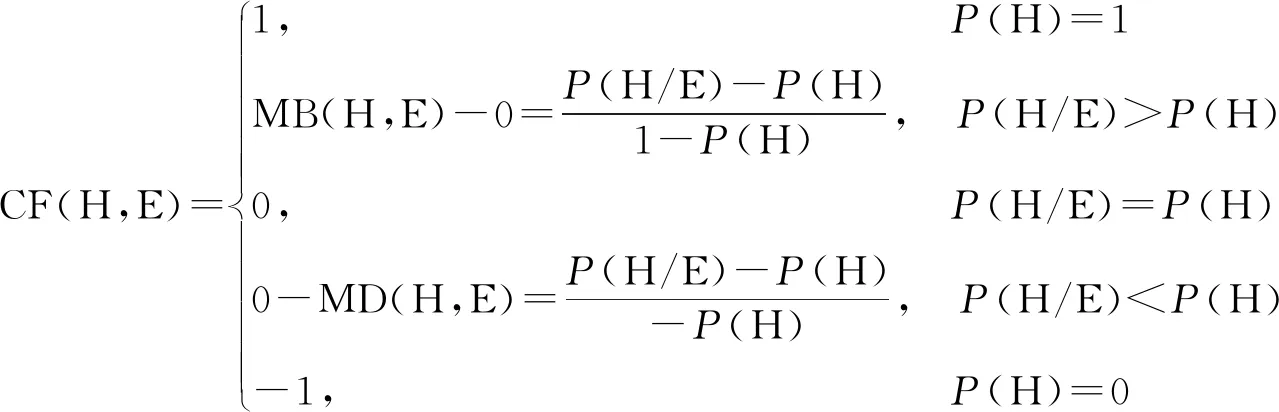
(1)

式中，MB(H,E)表示在证据E下对结论H的信任度的增加量；MD(H,E)表示在证据E下对结论H不信任度的增加量；P(H)表示结论H发生的先验概率；P(H/E)表示当E为真时H发生的条件概率[15]。基于不确定性推理理论，本文将采用可信度方法中的CF模型对矿体三维模型的不确定性表达及传递进行描述，以可信度作为不确定性传递过程的统一度量单位。为简化描述过程，本文将可信度值域[-1,1]归一化为[0,1]，即可信度取值为0时，结果为“假”，可信度取值为1时，结果为“真”，因此可信度值越大，不确定性越小，结果越接近“真”，反之不确定性越大，结果越接近“假”。不确定性传递计算过程中的主要算法包括合成计算和叠加传递计算，其中，合成算法是将多个证据进行组合，证据间为合取关系或析取关系，即分别以单一证据的最大值或最小值作为合成结果的可信度；叠加传递计算是以证据可信度为真时推导出的结论可信度为知识可信度，通过与证据可信度相乘，获得最终结论的可信度值，叠加传递算法描述为：

CF(H)=CF(E)×CF(H，E)

(2)

式中，CF(E )为证据可信度；CF(H,E)为知识可信度；CF(H)为叠加传递计算得到的结论可信度。

根据图1中矿体三维模型不确定性分布情况，将建模过程中各种误差产生的不确定性分为推理型不确定性和计算型不确定性两种类型。

推理型不确定性是难以通过计算或统计方法确定的误差，它可由专家根据地质资料或矿体的复杂程度进行解释和推断并赋予相应的可信度，如构建矿体表面模型过程中，当矿体形态简单、内部无夹石分支、矿体轮廓线上工程见矿点摆列规律且相邻剖面间见矿点数目差别不大时，根据剖面轮廓线建立的矿体表面模型拟合较好，即解译结果具有较高的可信度，因此该类型矿体圈定可信度可赋予较高值，如0.8～0.9，而对于存在断层、夹石和分支等情况的复杂矿体，在根据稀疏分布的采样数据进行剖面轮廓线重构时，该类型矿体表面模型可因人工解译的经验性和个体性差异而导致模型拟合度差，因此该类型矿体圈定误差可赋予较低可信度，如0.2～0.3。

计算型不确定性是指可根据解析法、经典误差理论等不确定性度量模型获得，并以标准差表征转换而来的可信度，如矿体三维建模过程中的勘探工程、岩性分层中的测量误差及品位模型插值计算误差等都可归入该类型。测量误差一般采用一阶Taylor展开式对其不确定性进行近似描述，由于一阶Taylor公式仅适用于线性传播函数，对于非线性的矿体三维不确定性明显存在估算精度不足的问题，如改用Taylor高阶展开式又会增加整体计算的复杂性，因此，考虑到测量误差不确定的计算难度，本文将该类不确定性归入推理型不确定性范围，其可信度赋值通过抽样统计方式获得。

矿体三维模型的不确定性表达与传递是一个复杂的多环节关联与耦合系统，多个输入与输出并存，本文以误差较为集中的矿体三维属性模型插值计算为对象，通过对该类计算型不确定性的算法解析，结合矿体三维建模各环节不确定性分布状况，对矿体多粒度模型的不确定性表达与传递机理进行探究。

2.2 矿体三维模型不确定性表达算法解析

多粒度矿体三维模型是根据矿体不同地质阶段逐步丰富的钻孔采样数据，以地质统计学理论为数学基础，分别采用克里格估值和序贯高斯模拟两种不同插值算法，为满足矿山企业不同层次需求所建立的具有多粒度特性的矿体模型，基本原理为：在矿体详查、勘探等采样数据稀疏且不完整阶段，利用序贯高斯模拟插值的整体统计性和空间相关性等特点，采用多次模拟的平均值建立可反映地质变量波动性的矿体三维模型；在矿体开拓、回采等钻孔密集、地质数据完备阶段，根据克里格估值的无偏估计和方差最优计算原则，建立精度较高且可精确估算储量的矿体三维模型。同时，根据序贯高斯模拟数学期望无限趋近于克里格估值的特性，在利用模拟算法建立矿体三维模型过程中，以克里格估算和序贯高斯模拟的平均值分别作为真值和近似值，以两者置信区间的置信度α为约束条件，根据α的不同取值定义不同的语义粒度，采用t检测方法得到对应的模拟计算次数，进而得到对应于克里格估值和由多次序贯高斯模拟均值所构建的不同语义粒度矿体三维模型。

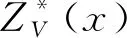
(3)

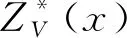
(4)

在依据样本方差估计母体方差的过程中，样本方差即估计方差S2，其定义为[17]：

(5)

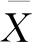
(6)

由式(6)可知，利用估计方差对母体方差估值的精确度与样本容量n存在必然联系，设母体方差σ2的误差区间为[(1-α)σ2,(1+α)σ2]，P为估计方差落在此误差区间的概率，因此χ2(n)分布的概率密度函数为：

(7)

故a≤χ2≤b的概率为：

P{a≤χ2≤b}=

(8)

式中，Γ(n)为伽马函数。

当利用估计方差(S2)对母体误差(σ2)进行估计时，则有公式[18]：

(1-α)σ2≤S2≤(1+α)σ2

(9)

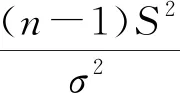
(1-α)(n-1)≤χ2≤(1+α)(n-1)

(10)

则有：

a=(1-α)(n-1)

b=(1+α)(n-1)

(11)

将式(11)带入式(8)中，可得：

P{(1-α)(n-1)≤χ2≤(1+α)(n-1)}

(12)

根据伽马函数定义，由式(12)可计算出不同样本容量(n)下估计方差(S2)落在其母体误差(σ2)指定区间的概率P，P值即表示估计方差的可靠性。因此，在克里格估值计算过程中，根据克里格方差和理论变差函数确定的邻域范围内的参考点数目，结合预先划定的无偏误差区间，即可获得以概率为表达的插值结果精度评定指标，并以此为依据转化为克里格插值算法可信度。

3 多粒度矿体三维建模的不确定性传递过程

矿体三维建模过程中的不确定性传递即模型构建中各环节不确定性的合并、叠加和传输至下一阶段的过程，为此，提出基于CF模型描述的多粒度矿体三维建模不确定性传递模型推理网络如图2所示，利用推理网络中可信度的传递来实现多粒度矿体三维建模的不确定性传递的描述。 从图2中可以看出，推理网络的初始证据可信度来源于矿山多源建模数据，多源建模数据集合中的所有不确定性经合成算法生成建模数据可信度，建模数据可信度与同样经合成算法生成的结构建模过程可信度进行叠加计算，形成矿体三维结构模型可信度。在利用结构模型建立多粒度属性模型过程中，根据模型用途分别采用估值建模和模拟建模方式进行插值计算，以此形成估值算法

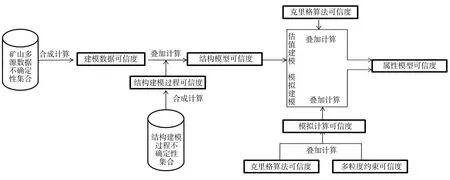
图2 多粒度矿体三维模型不确定性传递过程

可信度和模拟算法可信度，经与结构模型可信度进行叠加计算，最终完成三维属性模型的可信度表达。由前文可知，模拟建模过程由克里格估值和序贯模拟计算组成，因此其可信度由克里格估值可信度和多粒度约束可信度叠加计算生成，其中，多粒度约束可信度则由预先定义的约束置信度α转换而来。

多粒度矿体三维建模不确定性计算流程如下：

Step1：测量、解译和整理勘探地质剖面、钻孔样品等多源矿山建模数据，根据数据类型和专家经验，对所有数据产生的误差分别进行不确定性赋值并形成矿山多源数据不确定性集合，对集合内不确定性进行合成计算，生成建模数据可信度(D_CF)。

Step2：对矿体圈定、剖面轮廓线提取和重构、剖面多边形对应、矿体剖分等构模过程误差进行不确定性赋值，形成结构建模过程不确定性集合，对集合内不确定性进行合成计算，生成建模过程数据可信度(SMP_CF)。

Step3：通过对D_CF和SMP_CF的叠加计算，生成结构模型可信度(SM_CF)。

Step4：根据矿体数据基础和矿山企业需求的不同，对建立的具有多粒度特征的三维属性模型按模拟建模和估值建模两种类型分别计算其过程不确定性，即克里格估值可信度和模拟计算可信度。

(1)克里格估值可信度计算过程为：(a)经过实验变差函数计算和理论模型函数拟合，并根据搜索域确定插值样本和数目；(b)对样本进行克里格插值计算，建立矿体三维属性模型并得到克里格估计方差；(c)根据模型精度可接受范围，确定模型无偏误差区间，根据公式(12)和插值样本数计算估计方差可靠性概率P，将P值转换为克里格估值可信度(KC_CF)。

(2)模拟计算可信度的计算过程为：(a)对样本进行克里格估值，得到模拟计算目标值，同时依据上述克里格估值可信度计算过程，得到克里格估值可信度(KC_CF)；(b)将预先划定的置信度α转换为多粒度约束可信度(MGC_CF),同时以模拟计算目标值为真值，以置信度α为约束，利用进行多次序贯高斯模拟计算的平均值构建不同粒度的矿体三维属性模型；(c) 对KC_CF和MGC_CF进行叠加计算，生成模拟计算可信度(SC_CF)。

Step5：将Step3得到的结构模型可信度(SM_CF)分别与模拟建模和估值建模过程产生的克里格估值可信度(KC_CF)及多粒度约束可信度(MGC_CF)进行叠加计算，得到多粒度矿体三维属性模型可信度(AM_CF)。

4 应用实例与分析

在江西省城门山铜矿地质勘查数据的基础上，以Cu品位模型建立过程中的克里格插值计算为例，对误差较为集中的属性建模中克里格估值不确定性计算的有效性进行验证。

城门山铜矿为Cu、S、Mo共生的综合性矿床，伴生Au、Ag等稀有元素，主要矿体产状包括似层状、豆荚状、透镜状、带状及席状等类型。矿区勘查数据来源于矿山地质过程中钻孔资料，钻孔样品数共18 421件，结合样品中Cu、S、Mo等元素化学成分分析结果，完成20条勘探线和159个钻探工程数据的编录工作。以iExploration-EM(固体矿产资源量估算与矿体三维建模系统)为数据处理和建模平台，经单工程矿体圈定、剖面矿体圈定、轮廓线拼接等人工解译过程，形成实验矿区Cu矿体结构模型如图3所示。从图3中可看出，矿区共包含三个矿体，分别为矿体Ⅰ、矿体Ⅱ、矿体Ⅲ。经钻孔数据的特高品位值处理、钻孔样品组合、实验变差函数计算、理论变差函数结构分析与套合等步骤，建立Cu属性模型,在建模过程中，选取矿化较集中的12至14号勘探线区间大小为80 m×120 m×290 m的区域作为验证区块，该区块包含于矿体Ⅰ内，在验证区块内随机选取20个采样点作为验证块体，采样点Cu品位平均值为0.853，方差σ2为0.962。 将全样本的误差区间分别设定为[0.9σ2,1.1σ2]和[0.8σ2,1.2σ2]两个区域， 在验证区块内，首先利用不同数目的样本对选定的20个采样点经30次克里格法插值

图3 城门山矿区Cu矿体结构模型

计算分别得到其估值方差及其落在预定误差区间的概率，再利用公式(12)计算出相对应样本数下的计算方差落在预定误差区间的概率P，比较两种方法的计算结果如表1所示。从表1中可以看出，在相同的样本数下，克里格估值方差在预定区间的概率与利用公式(12)计算得到的计算方差落在指定区间的概率非常接近，表明两种方法得到的结果偏差较小，因此，在对克里格估值可信度进行确定的过程中，可以通过其插值样本的数目，由式(12)计算获得在指定误差区间内的以概率为表达的插值结果精度评定指标。

表1 克里格估值方差与数值计算方差落在指定误差区间概率比较(单位：%)Table 1 Comparison of the falling probability between Kriging interpolation variance and numerical calculated variance within the specified error interval

5 结语

(1) 对多粒度矿体三维模型的不确定性采用克里格插值计算方法，并对克里格方差进行可信度转换,提出了基于样本数的样本方差对母体方差的精度评估方法，并以此得到克里格估值计算过程中基于概率表达的精度评估指标，实现多粒度矿体三维模型的不确定性的定量评价。

(2)通过对试验区矿体样本方差与母体方差精确度的比较以及对样本克里格估值方差在指定误差区间内的概率进行统计分析，验证了多粒度矿体三维模型的不确定性的定量评价方法是有效的。