EMAT线圈导线宽度对螺栓表面涡流分布影响的仿真分析

黄文种，余 震，丁 旭

(1. 武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉，430081；2. 武汉科技大学机械传动与制造工程湖北省重点实验室，湖北 武汉，430081)

电磁超声(EMAT)是通过电磁场在金属试件上激励和接收超声波的一种换能方法[1]。由于具有独特的换能机制，即可以在不接触试件表面且不需对试件表面进行处理的情况下进行缺陷检测，EMAT在高强度螺栓在役检测领域具有明显的技术优势。

电磁超声换能器通过电磁线圈激发表面涡流，感应涡流在外加磁场作用下受到洛伦兹力的作用而产生电磁超声。电磁线圈结构和尺寸会对线圈的电流分布产生影响，进而影响到试件表面的涡流分布。近年来，随着计算机仿真技术精度的不断提高，有限元分析被广泛应用于实际工况下电磁线圈载荷分布的模拟[2-4]。王淑娟等[5]对用于铝板表面检测的电磁超声表面波换能器进行了三维有限元建模和仿真分析，结合正交试验，得到了工件表面涡流场分布与回折线圈之间距离、导线宽度等参数间的关系。张金等[6]以铝板为研究对象，建立曲折线圈EMAT检测过程的有限元模型，结合正交试验方法，分析了永磁体尺寸、线圈设计参数、线圈层数及层间距等因素对EMAT激励效率的影响。刘素贞等[7]借助ANSYS有限元仿真软件对电磁超声换能器进行仿真，在此基础上通过电磁结构耦合建立了声场模型，分析了表面波在试件中的辐射声场分布、指向性等规律。Tkocz等[8]以有限元法为辅助工具，开发出了一款可编程的高功率相位延迟电磁超声系统。目前，多数研究主要从线圈提离高度、线圈导线间距等宏观角度分析了线圈结构与所测试件表面涡流的关系，而有关电磁线圈截面尺寸对试件表面涡流分布的影响还报道较少。

基于此，本文基于理论分析和有限元仿真模拟，以两种不同结构的EMAT电磁线圈为研究对象，分析了每匝线圈横截面尺寸对所测试件表面涡流分布的影响，研究结果可为表面缺陷检测用超声探头电磁线圈的设计提供参考。

1 EMAT电磁线圈的换能机理

1.1 电磁超声探头线圈的结构

电磁超声探头的主要组成部分如图1所示，其主要包括探头外壳等部件构成的屏蔽层、用于提供偏置磁场的永磁铁和用于激发表面涡流的线圈，其中线圈结构直接影响试件表面的涡流分布，进而影响到探头的声场形态。目前，广泛使用的线圈形式包括螺旋线圈、跑道线圈、蝶形线圈和回折线圈等。图2所示为典型的跑道线圈与螺旋线圈的结构示意图。跑道线圈主要工作部分是线圈的直线区域，这种结构的线圈产生的涡流沿导线走向呈直线型分布，即产生沿直线分布的洛伦兹力，激发对称的声场；螺旋线圈主要工作部分为其环形结构，产生的涡流围绕着环形轴心呈轴对称分布，从而产生轴对称的洛伦兹力，激发轴对称的声场。

目前，电磁超声领域用线圈普遍采用印刷电路板(PCB)技术制作，每匝导线的厚度较薄，且沿厚度方向线圈尺寸变化不大，但是根据设计需要，线圈横截面宽度可以在一定范围内浮动。

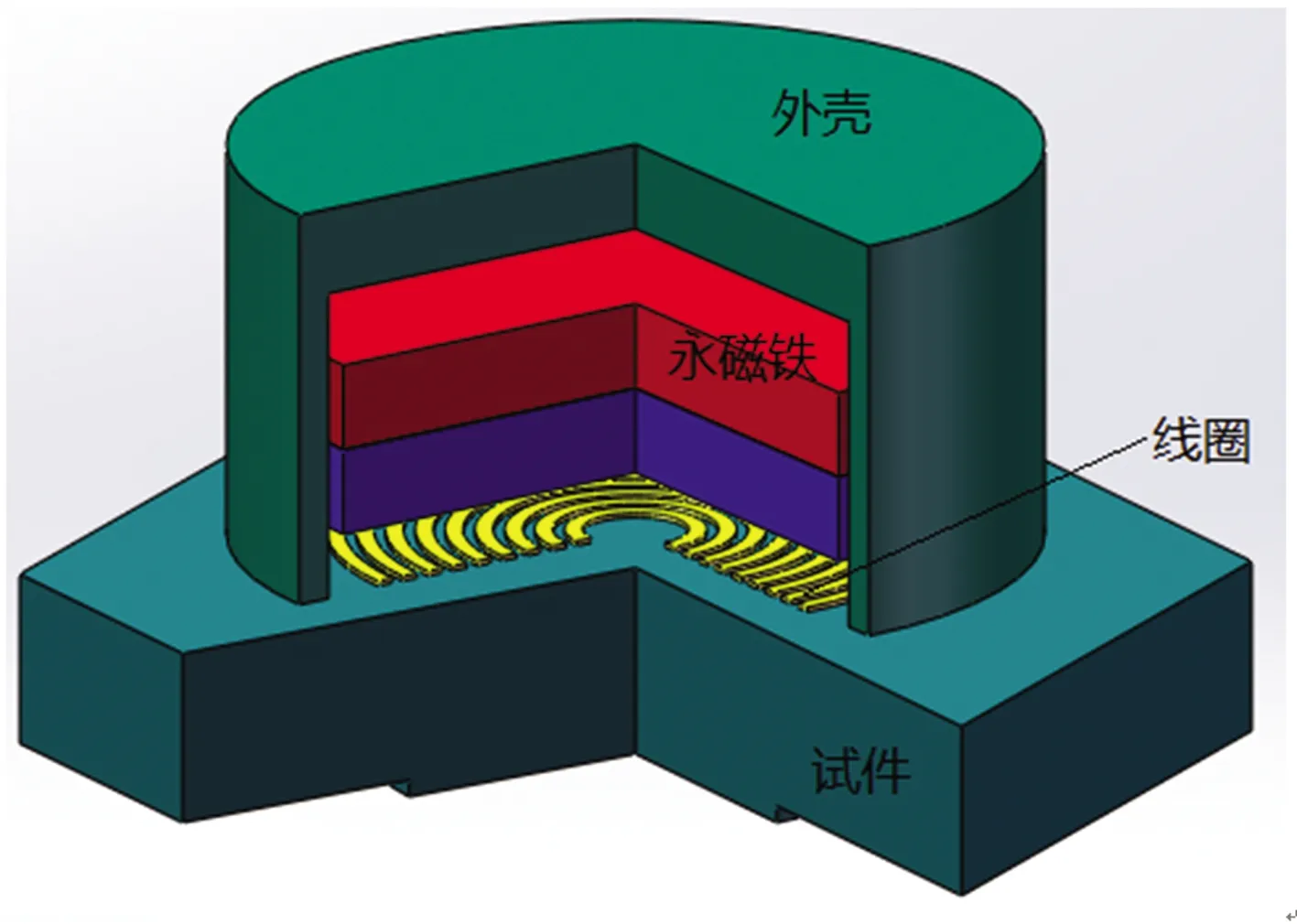
图1 螺旋线圈电磁超声探头结构

(a) 跑道线圈

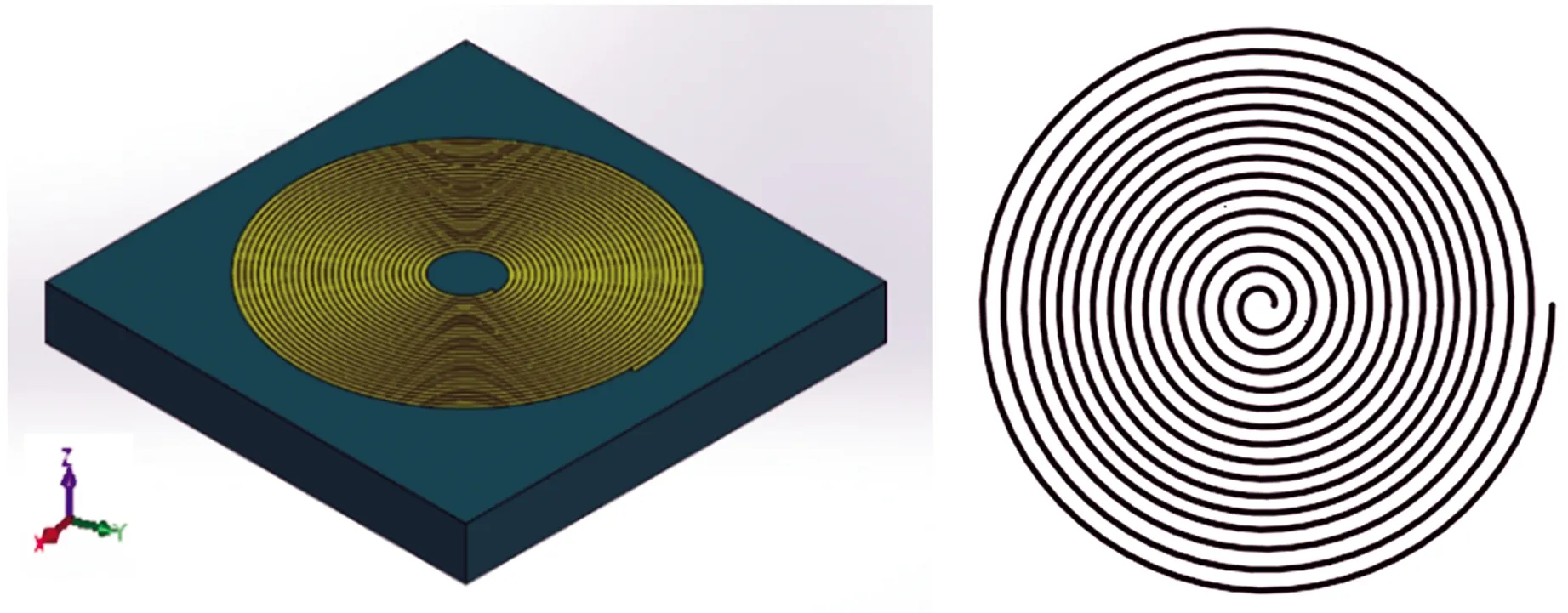
(b) 螺旋线圈

1.2 电磁超声探头的激励机理

电磁超声主要的激励机制为洛伦兹力，当试件为铁磁性材料时，还存在磁力和磁致伸缩效应作用。大多数情况下，磁力和磁致伸缩效应的激励远弱于洛伦兹力，可以忽略不计。试件表面洛伦兹力FL是由表面涡流和表面磁场相互作用产生的，可表示为：

FL=Jw×B

(1)

式中：Jw表示试件表面区域感生涡流密度，B为试件表面区域磁通密度。同一联通金属导体中没有电位差，故Jw=Je+Jd，Je为由发射线圈产生的交变磁场引起的感应涡流密度，Jd为该交变磁场产生的交变电场引起的位移电流密度，可由式(2)和式(3)表示：

Je=-jωσA

(2)

Jd=jωε(-jωA)

(3)

联立后可得：

(4)

式中：A为磁矢量势，ω为各电磁场的统一角频率，σ为导体电导率，ε为绝对介电常数。

电磁超声检测过程中，角频率ω的数量级一般为107，钢铁绝对介电常数ε的数量级为10-11，钢铁电导率σ的数量级为105，估算后可知式(4)中Jd/Je≪1，因而可以忽略位移电流项，即：

Jw=Je+JdJe

(5)

工件表面的磁场B由两部分组成，即永磁铁提供的偏置磁场B0和交流线圈产生的交变磁场Ba。电磁超声探头工作时，Ba相对于B0而言数值很小，可以忽略不计，即BB0。

综上所述，工件表面洛伦兹力可表示为：

FL=Je×B0

(6)

通常电磁超声探头会使涡流区域的偏置磁场大小与方向均匀且一致，因此，洛伦兹力分布主要由涡流分布决定。

1.3 表面涡流产生机理

当计算具有导电和介电特性材料中的交流电压和电流密度分布时，计算过程中特将电磁超声探头线圈导线中的交变电流看作已知分布规律的简谐交变电流。若将探头和试件简化为二维平面模型，则可对各场量作如下假设：①所有场量具有相同的角频率，但可以有不同的相位角；②在二维平面中，所有电流(包括电流源电流、感应涡流、位移电流)均垂直于二维平面，亦即对于二维平面中所有电流、磁矢势均只有垂直于模型平面的X分量，所有磁场均只有面内的Y分量和Z分量；对于二维轴对称平面模型，所有电流、磁矢势均只有周向θ分量，所有磁场均只有径向r分量和轴向z分量；③二维平面内无面内电流，电场强度只有垂直于平面的分量，所以电势在平面内应该为一个常量。将线圈电流看作简谐电流，则整个理想空间中的电磁场也为简谐场。

麦克斯韦方程组如下式所示：

(7)

(8)

(9)

(10)

式中：E为电场强度，B为磁通密度，ρ为电荷密度，μ为磁导率。

简谐时变电磁量有如下形式：

F(t)=Fmcos(ωt+θ)

(11)

式中：θ为初相位，Fm为电磁量幅值的空间分布矩阵，根据欧拉公式，式(11)可变换为：

F(t)=Fmcos(ωt+θ)=

R{Fm[cos(ωt+θ)+jsin(ωt+θ)]}=

R[Fmej(ω t+θ)]

(12)

磁矢势A、电势Φ与电场强度E、磁通密度B之间的关系为：

E=-Φ

(13)

B=×A

(14)

磁矢势A与电势Φ的关系可表示为：

×A)=(-jωA-·Φ)(σ+jωε)

(15)

2 涡流效应的线圈尺寸影响因素分析

(1)导体自感产生的趋肤效应

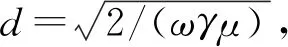
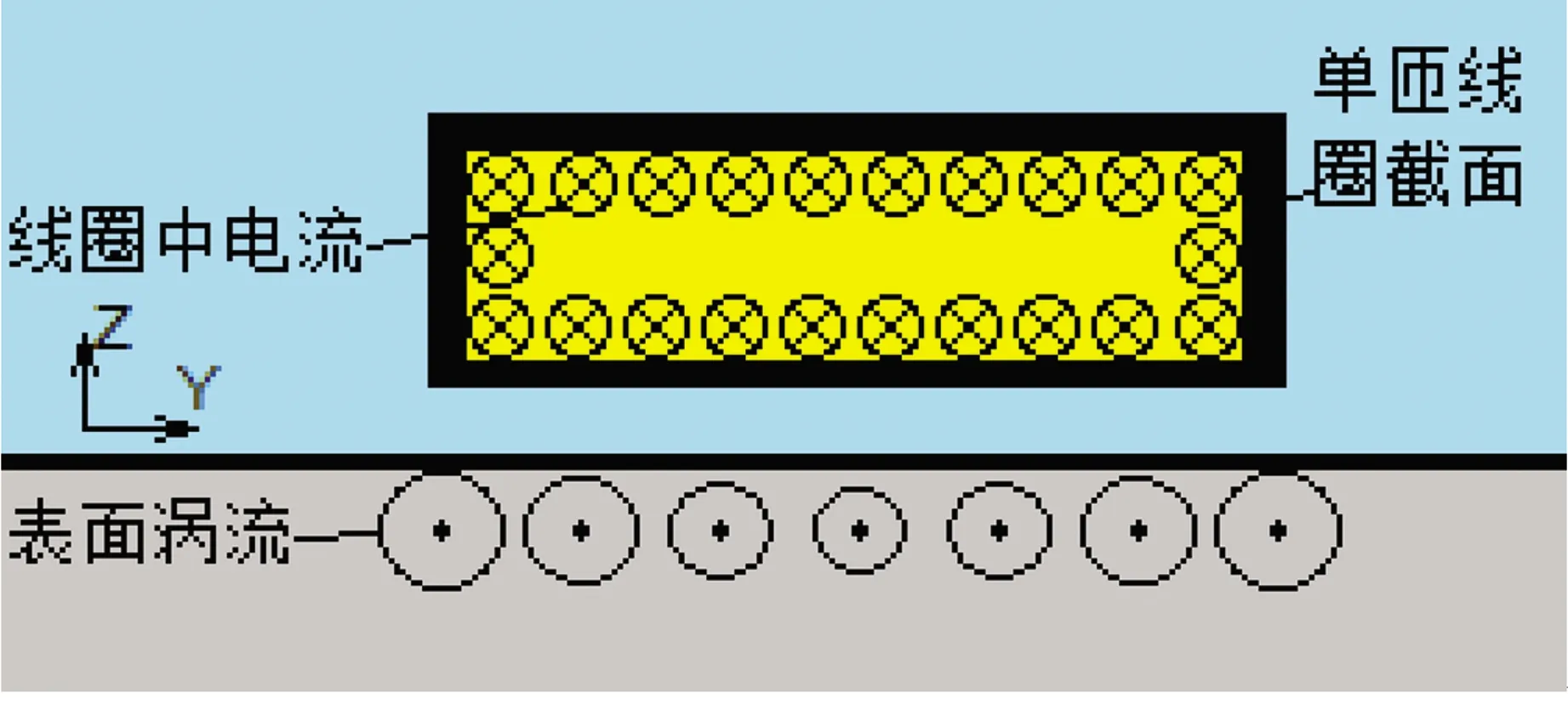
图3 趋肤效应下试件表面的涡流分布

(2)相邻导线间互感的影响

某匝导线的相邻导线会在该匝导线中产生感生电抗，而最外侧导线只有一侧存在相邻导线，这会导致电流在其中的分布情况与其他导线不同，如图4所示，对于线圈最外侧导线而言，远离线圈

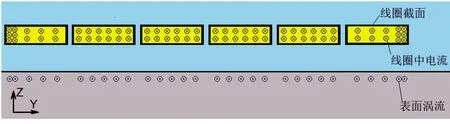
图4 导线互感作用下试件表面的涡流分布

中心一侧感抗更小，电流更容易从该侧流过，故外侧导线下方感应涡流要小于中间导线下方的感应涡流。

(3)线圈结构的影响

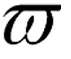
图5 螺旋结构线圈作用下试件表面的涡流分布

3 仿真分析

本文分别对直线型结构线圈和环形结构线圈进行建模，重点讨论了每匝线圈横截面尺寸对螺栓表面电磁场分布的影响。利用ANSYS Maxwell软件进行仿真分析，由于表面涡流场只受交变磁场影响，故本文不对永磁铁部分进行建模；另外，探头外壳等结构对交变磁场产生屏蔽效果，可将其统一简化为屏蔽层。基于此，本文所建模型均由外壳屏蔽层、试件、线圈和空气四部分组成。仿真过程中，试件材料设置为钢，远场介质为空气，外壳屏蔽层材料为铝，导线材料为铜，相应参数列于表1中，其中试件材料的相对磁导率见图6所示的B-H曲线。

表1 材料的物性参数Table 1 Physical parameters of the materials

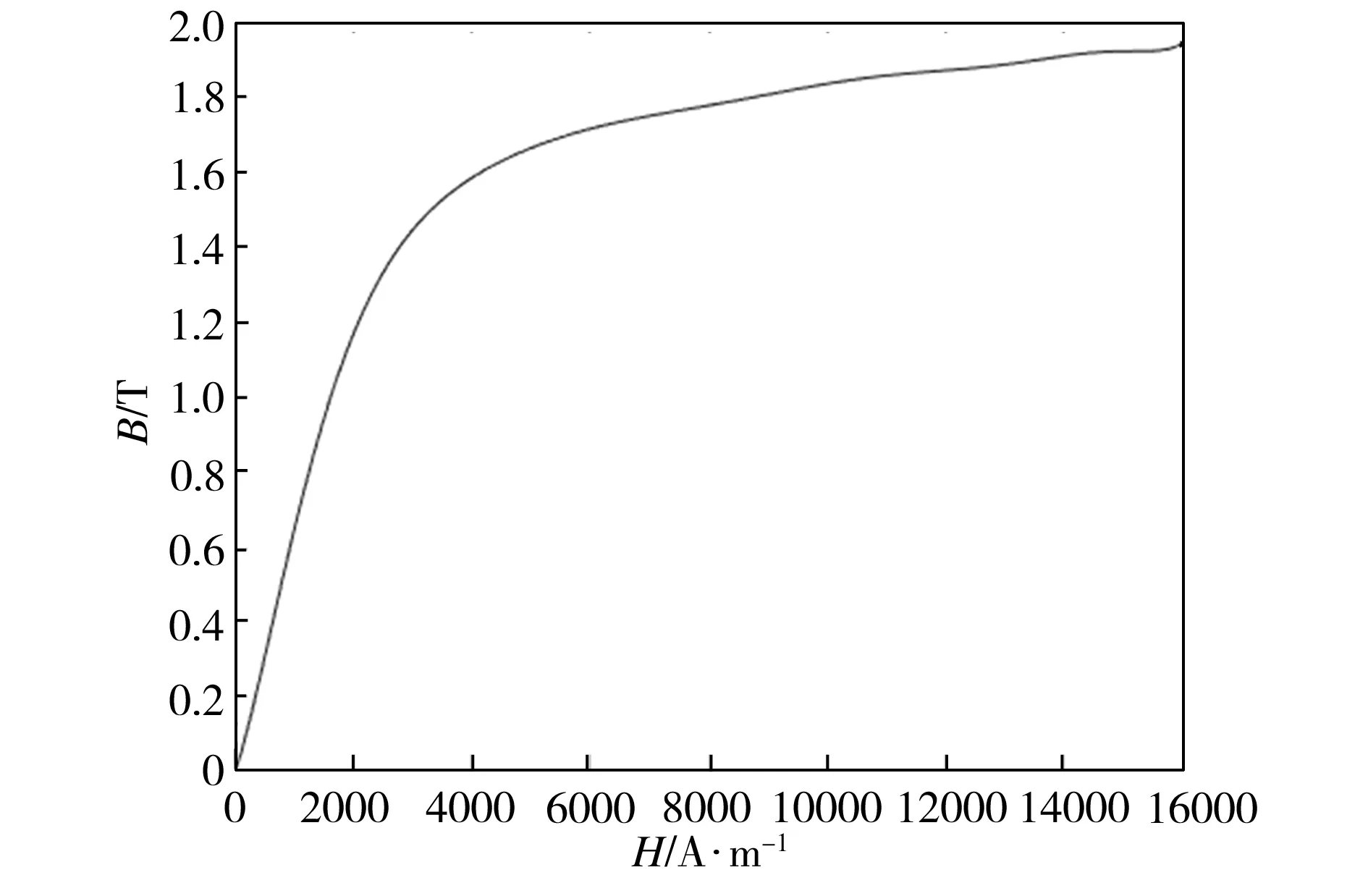
图6 螺栓端部材料的B -H曲线

3.1 直线型电磁线圈二维模型的涡流场分布

考虑到直线型超声探头电磁线圈的结构对称性，本文将其简化为直角坐标系二维模型，得到直线型电磁线圈的几何模型如图7所示，试件表面与屏蔽层间部分试件表面的有限元网络划分如图8所示，试件表面的网格尺寸设置为0.25 μm。仿真采用的参数如表2所示。图7中，线圈提离高度为0.5 mm，控制线圈整体宽度为22 mm，线圈厚度为0.035 mm，线圈包含若干匝，假设线圈填充率为100%，并将每匝之间的间隙设置为0，每匝导线宽度W为变量，通过改变W来调整每匝线圈截面的几何尺寸。

图7 直线型超声探头电磁线圈的二维模型

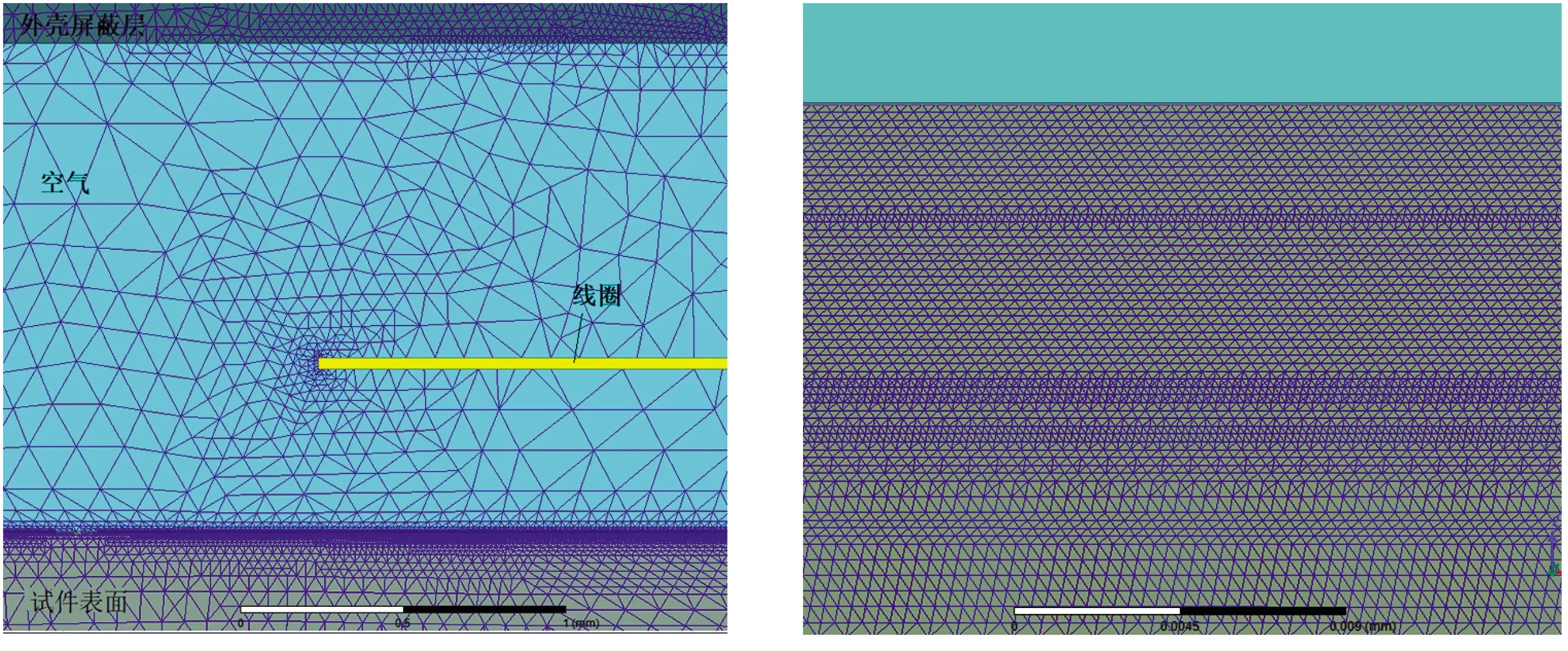
(a)试件表面与屏蔽层间部分

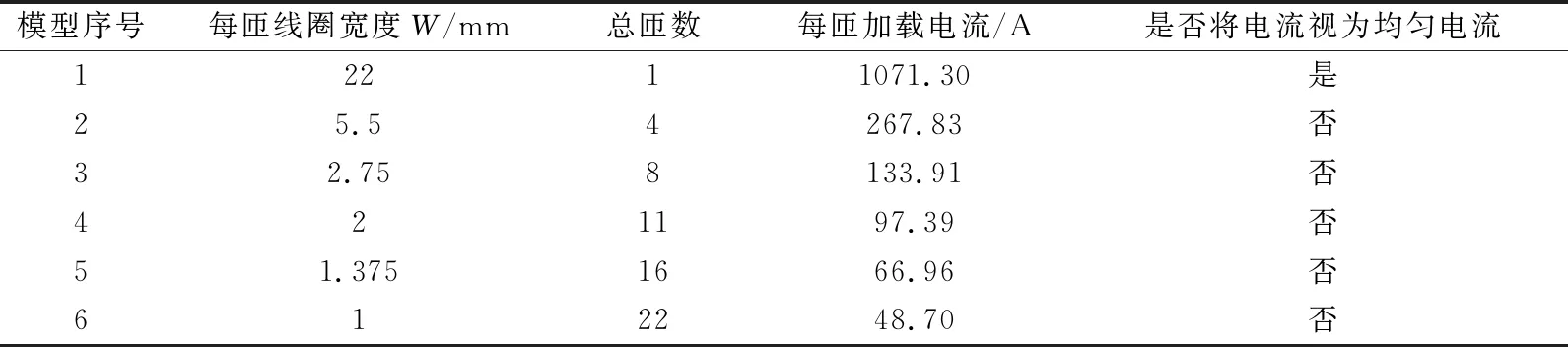
(b)试件表面趋肤层 图8 有限元模型网格划分Fig.8 Grid partition of finite element models表2 直线型线圈模型仿真参数Table 2 Simulation parameters of linear-coil model

向导线中添加电流激励，线圈的安匝数控制为1071.3 A，激励频率为2 MHz，每组模型加载的电流强度相同，各匝导线加载电流的相位相同。由表2所示的仿真模型参数可知，1#模型为对照组，控制导线中电流均匀分布；其他模型均为实验组，只控制每匝导线加载电流的大小，导线中电流的分布情况通过基于电磁感应原理的仿真分析计算得到。

通过仿真计算，得到直线型线圈二维模型螺栓表面的涡流密度幅值、磁场强度幅值的径向分量和轴向分量如图9所示。由图9可见，当考虑线圈中电流非均匀分布影响时，试件表面涡流密度幅值曲线的两侧均呈阶梯状下跌，而中间部分表面涡流密度基本不随导线宽度的变化而变化。若趋肤效应是造成导线中电流分布不均匀的主要因素，导线中边界的电流密度应该大于中间区域，其对应的表面涡流密度也应该随之呈两端大于中间的趋势，但仿真结果与该预期不符合。由此可以推断，导致线圈中电流分布不均匀的主要因素可能是相邻导线互感产生的感抗，而趋肤效应造成的影响相对较小。当线圈导线截面宽度等于1 mm时，表面涡流密度幅值、表面磁场强度幅值的径向分量和轴向分量结果均与将导线中电流看作均匀电流时的结果(1#模型)最接近，其中涡流密度幅值结果完全相等。

(a)表面涡流密度幅值 (b)表面磁场强度幅值的径向分量

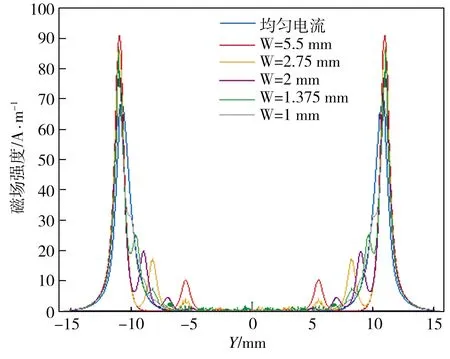
(c) 表面磁场强度幅值的轴向分量

3.2 环形线圈模型涡流场分布

考虑到探头结构的轴对称性，本文将环形结构线圈简化为圆柱坐标系二维轴对称模型，如图10所示。该模型以Z轴为轴心，线圈提离高度为0.5 mm，控制线圈的内径、外径、厚度依次为4、25、0.035 mm，该线圈包含若干匝，假设线圈填充率为100%，每匝导线之间间隙设置为0，每匝导线的宽度W为变量，通过改变W的数值来改变每匝线圈截面的几何尺寸，仿真用的模型参数列于表3中。

该模型的有限元网格划分结果与上述3.1章节直线型线圈二维模型相同。

图10 环型超声探头电磁线圈的二维模型

表3 环型线圈模型仿真参数

图11所示为仿真计算得到环形线圈二维模型螺栓表面涡流密度幅值、磁场强度幅值的径向分量和轴向分量。从图11可以看出，当考虑线圈中电流非均匀分布影响时，螺栓表面涡流密度幅值、表面磁场强度幅值的径向分量和轴向分量均呈现波浪形特征，当宽度W取不同值时，模型靠近轴心处对应的磁场强度均强于远离轴心处的磁场强度，亦即波形曲线的波峰位置更靠近于轴心一侧，这表明各模型靠近轴心的一侧电流密度要大于远离轴心的一侧。导致线圈中电流分布不均匀的主要因素是线圈的几何形状，而趋肤效应造成的影响相对较小。当线圈截面宽度W为0.3 mm(对应绿色曲线)时，表面涡流密度幅值、表面磁场强度幅值的径向分量和轴向分量均与将导线中电流看作均匀电流时的情况(1#模型)最接近，其中涡流密度幅值结果完全相等。

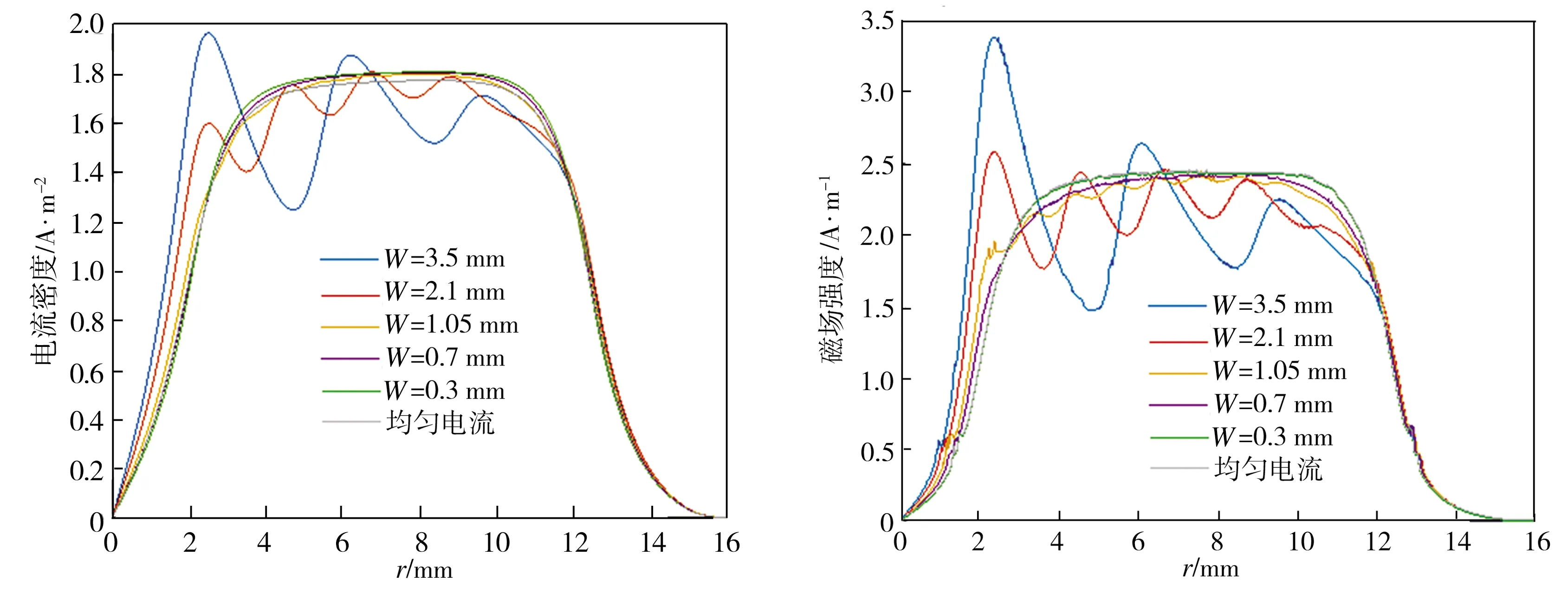
(a)表面涡流密度幅值 (b)表面磁场强度幅值的径向分量

(c) 表面磁场强度幅值的轴向分量

4 结论

(1)对于可简化为直角坐标系下二维模型的跑道型超声电磁探头线圈，线圈在紧密排布情况下，影响线圈中电流分布的主要因素是相邻线圈产生的感抗，当线圈每匝导线宽度小于1 mm时，表面涡流分布与加载均匀分布电流时的情况相同，故可以将线圈中的电流看作均匀分布的电流。

(2)对于可简化为二维轴对称模型的环形线圈，当线圈在紧密排布情况下，影响线圈中电流分布的主要因素是线圈的环形结构，当线圈每匝导线宽度小于0.3 mm时，试件表面涡流分布情况与加载均匀电流时的结果最为接近，此时，可以将线圈中的电流看作均匀分布电流。