振动载荷下固体推进剂粘接界面剪应力及损伤分布

王 鑫,卢洪义,赵汝岩,王玉峰

(1.中国人民解放军91851部队, 辽宁 葫芦岛125000; 2.南昌航空大学, 江西 南昌 330063; 3.海军航空大学, 山东 烟台 264001)

引 言

固体火箭发动机破坏模式中，粘接界面的破坏是装药发动机结构完整性破坏的关键。国外失效的固体发动机中有三分之一是粘接界面脱开引起的，尤其是推进剂与衬层的粘接界面[1-4]。良好的界面粘接性能可以确保推进剂装药按设计燃烧。若出现脱粘现象，将导致装药燃面发生变化，从而影响发动机的内弹道特性，严重则导致点火失败。

固体火箭发动机一经生产就经历固化降温产生的温差载荷、运输过程中的振动与冲击等载荷。对于需经历立式值班状态的固体发动机而言，还需经历长期立式贮存的重力载荷和海洋环境引起的低频振动载荷，复杂的值班环境会使粘接界面产生损伤，加速粘接界面力学性能的变化。然而在立式贮存过程中，粘接界面所承受的并非拉伸或者压缩应力，而是剪切应力，仅以粘接试件扯离试验结果作为衡量立式贮存损伤情况并不准确[5-6]。

基于此，阳建红等[7]开展了固体推进剂的多角度剪切力学性能试验研究，但并无推进剂及粘接界面剪切试验的相关标准。邱欣等[8]和杨明[9]也先后开展了粘接界面的疲劳和蠕变试验研究，获取了相应的本构方程，为粘接界面损伤计算提供了依据。曲凯[10]和张波[11]先后通过推进剂粘接界面定应力往复剪切试验，获取了界面疲劳损伤特性；并基于有限元分析计算的应力结果，计算了舰载条件值班一年的累积损伤，但未考虑粘接界面的蠕变影响。王鑫[12]将振动载荷近似为正弦函数，通过固化降温、重力与振动载荷的耦合有限元分析，获得艇载固体发动机装药的耦合损伤。但文献[10-12]所选取的振动载荷并非实测载荷，虽然具有一定的代表性，但与实际结果还存在一定偏差。

本研究以某型立式贮存固体火箭发动机为研究对象，开展了值班过程振动载荷监测。并基于数据处理结果，分别开展温差/重力载荷和温差/实测振动载荷下的有限元分析，获取立式贮存过程粘接界面剪应力变化历程及分布规律。在此基础上，结合粘接界面的剪应力蠕变和疲劳试验结果，计算粘接界面路径上各位置的累积损伤。

1 数值模拟

1.1 发动机模型的建立

某型固体火箭发动机燃烧室由壳体、绝热层、衬层、装药、前后封头等结构组成。由于绝热层和衬层厚度较小，且材料属性相近，故将二者看作一个整体，并在其中预设人工脱粘结构。忽略前、后裙以及前、后接头等对发动机装药及粘接界面影响较小的部组件。发动机具有几何对称结构，取三维有限元模型的一半，如图1所示。

图1 发动机三维模型Fig.1 Three-dimension model of motor

1.2 载荷及计算工况

在值班过程中，某型固体火箭发动机处于立式贮存状态，并需经历复杂的海洋环境，长时重力和低频振动载荷对发动机粘接界面会产生集中应力。立式贮存状态下，用界面处的剪应力衡量其损伤及破坏情况更贴合实际情况。

在值班之前，发动机需经历固化降温、公路运输等过程。在此忽略公路随机载荷，仅考虑固化降温对后续值班过程的影响，分别开展基于固化降温和重力/振动载荷联合作用下的数值模拟计算研究，具体加载方式参见参考文献[12]。根据载荷对称性，两计算过程分别选用1/16模型和全尺寸模型。

1.3 振动载荷及数据处理

振动载荷的选取基于实测数据。由于监测结果较为分散，选取连续性较好的100s作为最终结果，原始信号如图2所示，其中X、Y和Z分别代表导弹垂荡、横摇和纵摇3个方向。

图2 振动载荷原始信号Fig.2 Original signals of vibration loading

由图2可知，从振动信号来看，该监测条件下3个方向加速度值均小于0.2g，加速度幅值在0.4g以内。

频域振动信号如图3所示，3个方向振动信号频率小于0.5Hz，大小约为0.1Hz，即振动周期约为10～11s。

图3 频域振动信号处理结果Fig.3 Processing results of frequency domain vibration signals

对采集数据进行处理，消除趋势项后进行平滑处理如图4所示，将图4数据结果作为后续模拟计算的输入条件。

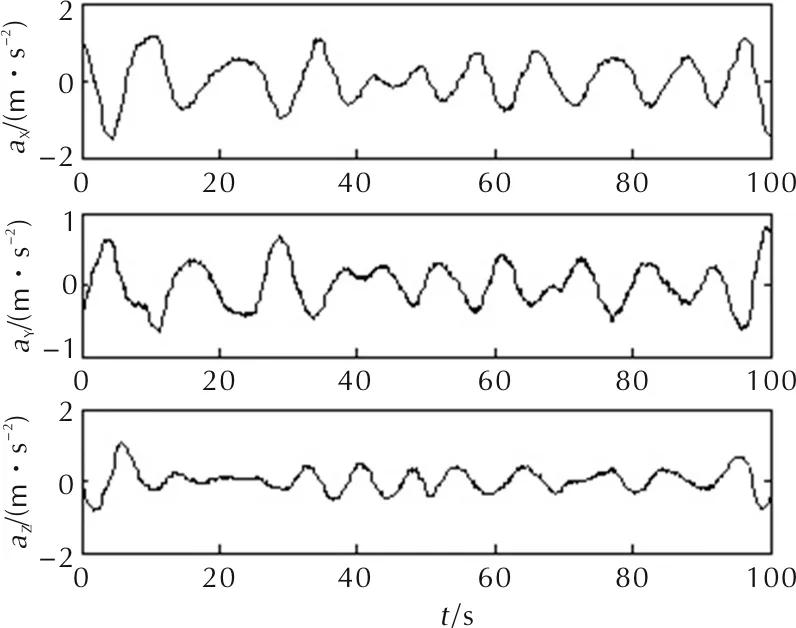
图4 振动载荷处理结果Fig.4 Processing results of vibration loading

1.4 剪应力选取

在ABAQUS软件中，Tresca应力表示主应力之间的最大差值，一般表示为：

Tresca=σ1-σ3

(1)

式中：σ1和σ3为第一和第三最大主应力。

定义剪应力τ为：

(2)

因此剪应力分布与Tresca应力分布规律一致，最终选取Tresca值衡量剪应力变化及分布规律，仅存在2倍的数值差异。

2 结果与讨论

2.1 重力载荷结果分析

在固化降温和重力联合载荷作用下，界面处剪应力分布规律如图5所示，在前、后人工脱粘根部有局部区域的应力集中，靠近前人工脱粘区域处界面剪应力较大，剪应力沿界面路径差值在5倍左右。

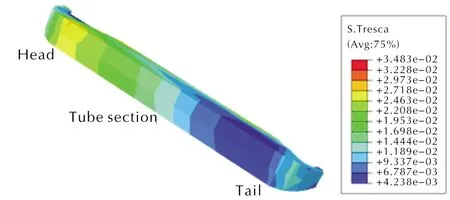
图5 重力载荷作用下界面剪应力云图Fig.5 Interface shear stress contour under gravity loading

位移云图如图6所示，由于装药与衬层结构设置了绑定约束，故轴向位移值变化较小，在1.5mm左右，因前、后人工脱粘结构应力自由，且受轴向重力作用，故前人工脱粘层前缘位移最大。

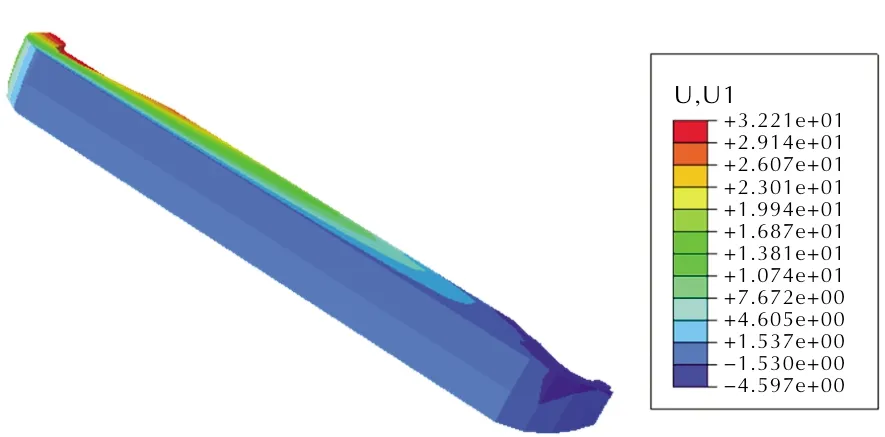
图6 重力载荷作用下界面轴向位移云图Fig.6 Axial displacement contour of interface under gravity loading

虽然重力作用下，界面处因绑定接触的设置，位移没有发生变化，界面剪应力也远达不到粘接界面的最大剪切强度(0.486MPa)，但立式贮存下，界面受长期恒定或者变化的剪应力作用，累积损伤不可忽视。在界面处选取3个不同位置(见图5)，绘制其重力作用下剪应力—时间历程曲线，如图7所示。

图7 不同位置剪应力—时间曲线Fig.7 Shear stress—time curves at different positions

从图7可以发现，固化降温后，粘接界面各处在0～0.02MPa之间产生不等的初始预应力，随着时间的增加，界面剪应力减小，并逐渐趋于稳定，尤其对于靠近中孔和尾部各位置而言，可近似认定为恒定值。

2.2 振动载荷结果分析

在固化降温和实测振动载荷联合作用下，界面应力云图分布如图8所示。

图8 振动载荷作用下界面剪应力云图Fig.8 Interface shear stress contour of under vibration loading

从图8可以看出，界面分布规律与重力作用下基本一致，即前人工脱粘结构附近有明显的应力集中，界面剪应力最大值为0.02MPa左右；此处未给出位移变化云图。

在周期性的振动载荷作用下，界面各处产生幅值不等的周期性应力，从几十帕至千帕不等，以头部某位置为例，绘制其剪应力—时间历程曲线，如图9所示。

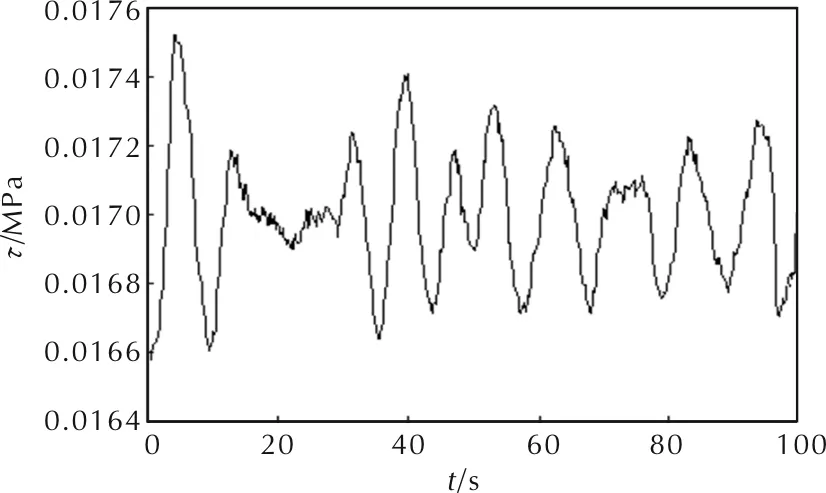
图9 振动载荷作用下某点剪应力—时间历程曲线Fig.9 Shear stress—time process curve of a point under vibration loading

从图9可以看出，100s内，剪应力循环数在12个左右，接近加速度周期数，即10～11s；该点最大应力幅值在1000Pa左右，最小应力幅值在100Pa左右，相差近10倍。

2.3 界面应力分布分析

为了更清晰地看出不同载荷作用下界面各处的剪应力随时间的分布规律，沿头部-中孔-尾部处绘制粘接界面某一路径，以1/16模型为例，路径为图10中加粗部分。为保证路径一致，全尺寸模型选取对称结构的相应位置。

图10 粘接界面路径示意图Fig.10 Schematic diagram of bonding interface path

两种载荷作用下界面剪应力沿路径和时间的分布如图11所示。

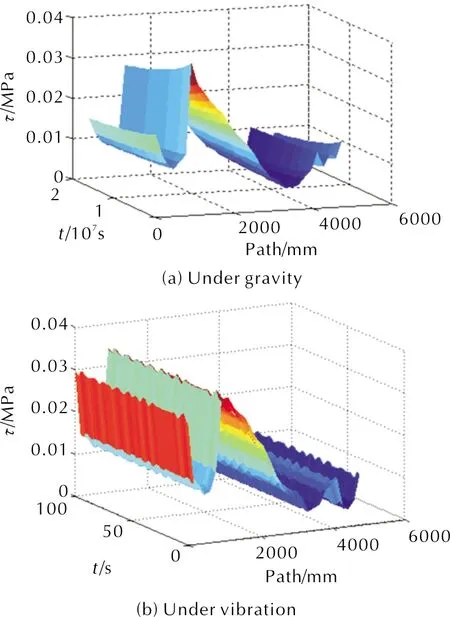
图11 重力载荷作用和振动载荷作用下剪应力沿路径分布Fig.11 Shear stress distribution of interface along the path under gravity and vibration

图11(a)表明，路径各处趋近于定剪应力变化，药柱中孔界面应力逐渐降低；图11(b)表明，路径各处呈现周期性变化的应力，且变化规律基本一致。

总体来看，两种载荷作用下剪应力沿界面变化规律趋于一致，最大应力均出现在前人工脱粘附近，也进一步印证了人工脱粘结构的应力释放作用。但疲劳损伤依据剪应力幅值变化而计算，故还需进一步深入研究。

2.4 损伤计算

2.4.1 损伤理论及本构方程引用

整体而言，麦克尤恩的《时间中的孩子》用文学之镜映衬了斯蒂芬丢失的那个孩子，在自然之镜中反思了丢失的那个孩子在自然空间、社会空间与精神空间所受到的种种磨难。尽管斯蒂芬没有能够找回自己的孩子，但是这个悬而未决的隐喻结尾却展示了积极的可能性：随着时间的流逝，斯蒂芬与妻子孕育着新的生命，《时间中的孩子》的荒原镜像伴着“一声哽咽，接着是一声清亮的啼哭”(《时》：239)。不再是一种虚幻中的文学叙事，它被再次拉入现实社会并充满未来生命的勃勃生机。这最终也让麦克尤恩完成了对《时间中的孩子》标题隐喻的一个完美解释：在时间中丢失的孩子，最终会在时间中找寻回来。

利用损伤力学来分析装药/粘接界面的损伤，以低周疲劳损伤与蠕变损伤的损伤模型为基础[13]。令Df表示疲劳损伤，Dc表示蠕变损伤，则两种损伤的表达式为：

(3)

(4)

式中：Ni和Nfi表示试件在剪应力幅值下的往复拉伸次数和往复拉伸破坏次数;t和tfi表示试件在剪应力下的加载时间和加载破坏时间。

且参考推进剂疲劳-蠕变交互损伤[14-15]，认为在二者的作用下粘接界面的耦合损伤与推进剂耦合损伤规律相同，及总损伤大于二者之和，用D表示，即:

(5)

2.4.2 损伤计算结果分析

根据线性损伤理论，并分别参考文献[10]和[9]中粘接试件的疲劳和蠕变本构方程，如式(6)和式(7)所示：

(6)

(7)

式中：N为粘接试件的剪切疲劳破坏次数；Δτ为振动过程中的剪切应力；t为粘接试件的蠕变破坏时间；σ为蠕变过程中的剪切应力。

基于此，利用式(3)和式(4)根据应力分布及变化情况计算累积损伤，其中蠕变剪应力参照图7，对于其随时间变化的情况，选取应力均值作为计算依据，疲劳损伤依据雨流计数法应力计数后计算得到[16]。

虽然路径各点处蠕变剪应力值最大相差几倍，但应力基数较小。从公式(7)计算发现，蠕变应力从0.05MPa降至0.005MPa时，各点蠕变破坏时间相差不到1个数量级，因此各点蠕变损伤相差不大。图12为关键点的损伤—时间历程曲线和贮存半年的界面蠕变损伤分布。

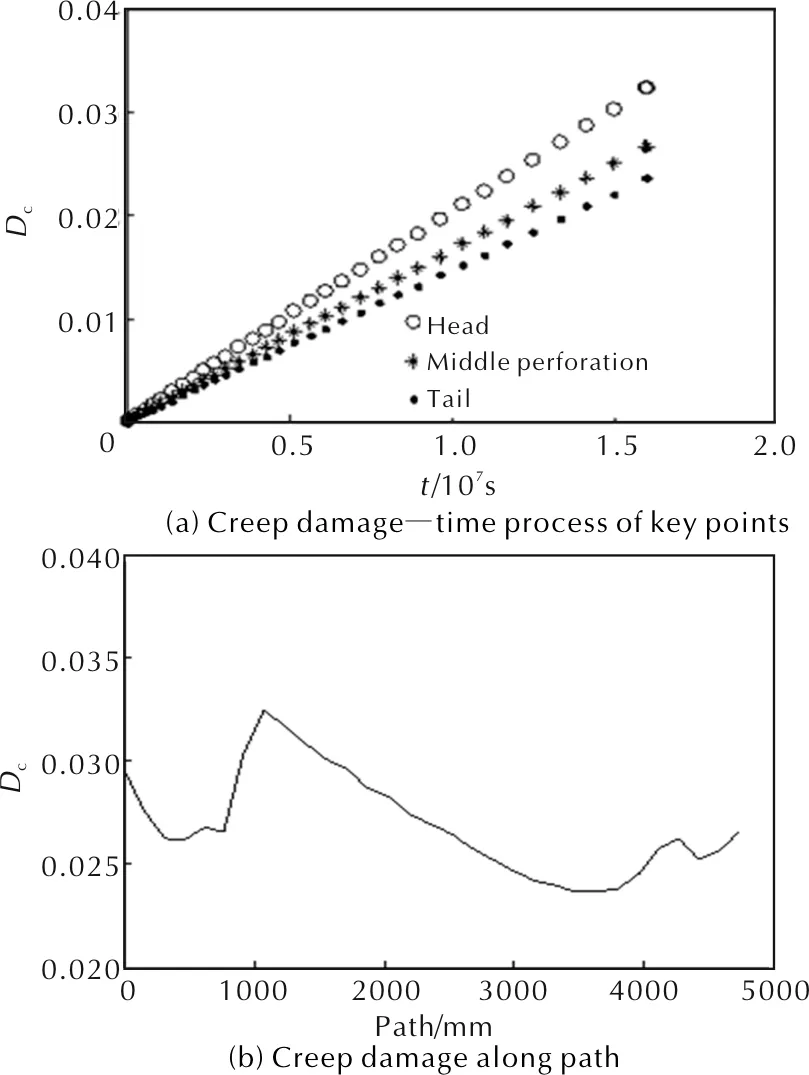
图12 关键点和关键路径蠕变损伤Fig.12 Creep damage of the critical points and critical path

从图12可以看出，蠕变损伤随时间线性变化，定义损伤系数α为：

(8)

得到最大蠕变损伤系数为2.03×10-9，路径各点损伤最大相差30%。

与蠕变损伤类似，界面各处的疲劳应力幅值差值对应的疲劳破坏次数相差较小，因此各位置疲劳损伤相差同样较小。经计算，100s内头部疲劳损伤为1.59×10-7，对应损伤系数为1.59×10-9。路径各点的疲劳损伤如图13(a)所示，由于相临位置的应力变化规律接近，故存在损伤相同的情况，损伤最大相差20%左右。根据式(5)计算界面立式贮存累积损伤，如图13(b)所示。由于没有针对粘接界面开展相应交互试验，故不考虑其交互项。

图13 疲劳损伤和累积损伤沿路径分布Fig.13 Distribution of fatigue damage and cumulative damage along the path

经计算，发动机立式值班半年时粘接界面累积损伤为5.79%，发生在前人工脱粘层附近的装药和衬层粘接界面处，是考虑交互项时装药损伤的2.64倍[15]，若考虑交互项，累积损伤值将更大。

3 结 论

(1)在重力载荷的作用下，粘接界面各位置剪应力随贮存时间逐渐降低，但变化趋势较小，可近似于常数，前人工脱粘结构附近界面应力最大。

(2)在振动载荷的作用下，随贮存时间增加，粘接界面剪应力呈现周期性变化，剪应力幅值在1000Pa左右，且路径各点变化规律一致。

(3)蠕变损伤、疲劳损伤贮存时间都呈线性关系，损伤系数数量级在10-9。若不考虑二者之间的交互项，发动机立贮值班半年时，界面累积损伤可达5.79%。

(4)在进行振动载荷的数值模拟计算时，仅选用100s监测数据代替整个贮存值班过程中的振动过程并不完全准确，且计算交互损伤时并未考虑交互影响；同时在通过粘接试件拟合的疲劳损伤本构方程计算界面损伤时，并未考虑粘接结构在自然贮存和值班过程中存在的老化影响，与实际情况存在偏差，应作为后续研究的主要内容。