基于非线性三步法的DCT两挡起步控制策略研究

叶珂羽 刘振宇 唐立中 顾强 刘奇芳

（1.中国第一汽车股份有限公司新能源开发院，长春 130013；2.汽车振动噪声与安全控制综合技术国家重点实验室，长春 130013；3.吉林大学，控制科学与工程系，长春 130025）

主题词：两挡起步控制 双离合器自动变速器 轨迹跟踪 非线性控制

1 前言

双离合器自动变速器（Dual Clutch Transmission，DCT）是一种结构紧凑、传动效率高且可实现无动力中断换挡的自动变速器，已经得到广泛应用。目前，装备DCT的车辆起步过程多借鉴机械式自动变速器，即采用1 个离合器承担起步力矩的单挡起步方法。针对单挡起步的控制方法研究较多，模型预测控制[1]、模糊控制[2]以及线性二次型优化控制[3]等方法均被应用于此问题。然而，长期基于单挡起步会造成2 个离合器磨损不均匀，不利于延长离合器总成的使用寿命。

车辆动力总成系统是一个非线性、强耦合系统，对于DCT 汽车起步过程，控制稍有不当就可能出现系统振荡、功率循环[4]或者发动机反拖甚至熄火等问题。基于DCT特有的双离合器结构，控制2个离合器同时参与起步过程是一种合理有效的解决方法，若控制得当，可达到快速、平顺的起步效果，同时可有效平衡2 个离合器的磨损，但这加大了起步控制难度。针对双离合器联合起步控制，基于最优控制理论[5-6]的方法被应用于此问题并取得了一定的效果，但是仍存在一定的局限性，即算法复杂程度高、工程实现较困难。

本文针对2个离合器联合起步控制问题，提出一种基于非线性系统三步控制方法[7-8]的起步控制策略，通过跟踪车速期望曲线转换得到的车轮转速曲线，对2个离合器传递力矩进行控制，达到换挡控制指标要求，并可根据需求灵活选择起步期望车轮转速曲线，实现快速、平顺且满足驾驶员加速期望的起步过程，同时延长双离合器总成的寿命。

2 DCT起步动力学模型及性能评价指标

2.1 起步过程动力学模型

图1 所示为DCT 起步动力学模型示意，其中Je、Jc1、Jc2、Jw分别为发动机、离合器C1 从动部分、离合器C2 从动部分、车轮的转动惯量，be、bc1、bc2、bw分别为发动机、离合器C1、离合器C2、车轮的粘性摩擦系数，ωe、ωc1、ωc2、ωf、ωd、ωw分别为发动机、离合器C1、离合器C2、主减速器、驱动轴、车轮的转速，Te、Tc1、Tc2、To、Td、Tw、TL分别为发动机转矩、离合器C1、离合器C2传递转矩、主减速器输出转矩、差速器输出转矩、车轮处转矩、车辆阻力矩，i1、i2、if分别为1挡、2挡和主减速器传动比。

图1 DCT起步动力学模型示意

DCT 传动系统是一个多质量、多自由度、耦合程度较高的非线性系统。为了简化模型，考虑其主要的动力学特性，忽略轴的横向振动、齿轮间隙、温度对变速器系统的影响等进行传动系建模。根据牛顿第二定律，发动机力矩平衡方程为：

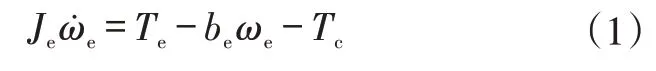
式中，Tc=Tc1+Tc2为离合器传递的转矩。

离合器从动部分与传动轴刚性连接，离合器力矩平衡方程为：

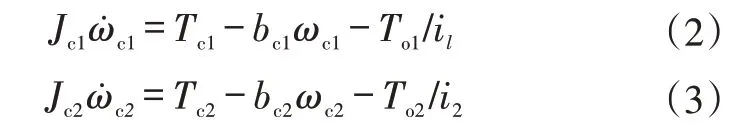
式中，To1、To2分别为1 挡、2 挡齿轮传递的转矩；对于DCT，1挡和2挡共用输出轴，对应的主减速比均为if。

主减速器处动力平衡方程为：

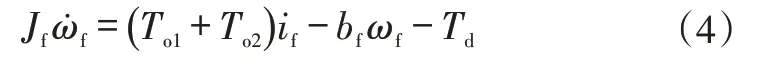
式中，Jf为主减速器转动惯量；bf为主减速器粘性摩擦系数。

记To=(To1+To2)if为主减速器输出转矩，To经驱动轴传递到轮胎，克服车辆阻力驱动整车运动，驱动轴处动力平衡方程为：

式中，Jd为驱动轴转动惯量；bd为驱动轴粘性摩擦系数。

假设驱动轴与主减速器是刚性连接的，即满足ωw=ωd=ωf，车轮处的动力学模型可表示为：

式中，Jw_equ=Jw+Jd+Jf为车轮等效转动惯量；bw_equ=bw+bd+bf为车轮等效粘性摩擦因数。

根据汽车行驶方程，车辆阻力矩TL由滚动阻力、空气阻力、坡道阻力、加速阻力4个部分构成：

式中，m为汽车质量；g为重力加速度；f为滚动阻力系数；α为道路坡度；CD为空气阻力系数；A为迎风面积；v为车速；δ为旋转质量换算系数；rw为车轮半径。

2.2 起步过程性能评价指标及起步控制目标

汽车起步过程的评价指标通常包括冲击度、滑摩功和起步过程时间[9]。

2.2.1 起步冲击度

考虑平路无风情况起步车速低，忽略风阻的影响，对式（7）求一阶导数得到冲击度的近似表达式为：

可以看出，起步过程中，与冲击度直接相关的为2个离合器的转矩变化dTc1/dt和dTc2/dt，所以控制好起步冲击的直观表现为控制汽车加速度，而达到良好控制效果的关键即是控制好2个离合器的转矩变化。

2.2.2 起步滑摩功

离合器C1和C2的滑摩功Wc1、Wc2可表示为：

式中，t0和t2分别为起步开始时刻和起步结束时刻。

起步时间越长，则滑摩功越大，而换挡冲击越小。一般情况下，减小冲击度需要通过增加离合器的滑摩来实现，在存在转速差的情况下，若离合器滑摩时间过长，就会产生大量滑摩功，对起步和离合器寿命造成不利影响。因此，在起步控制过程中，如何平衡冲击度和滑摩功是达到良好的起步控制的关键。

2.2.3 双离合器起步控制目标

基于本文提出的控制方法，提出双离合器起步控制目标为：

a.尽可能平衡2 个离合器在起步过程中的滑摩功，延长使用寿命。

b.起步冲击度尽可能小，满足|j|≤10 m/s3[8]。

c.为防止离合器烧蚀，离合器每次接合单位面积滑摩功小于0.4 J/mm2[8]。

d.车轮转速跟踪控制误差小于1 rad/s。

3 DCT起步控制策略

3.1 起步控制策略总述

根据DCT 的动力学特点及期望的控制目标，本文将起步控制过程分为以下4个阶段：

a.0～t0阶段，为消除空行程阶段。从整车上电、离合器充油开始，始终控制离合器压力达到将要开始传递力矩的点（Kisspoint点），当制动踏板完全松开且离合器压力达到Kisspoint点压力，该阶段结束。该阶段离合器主、从动部分未开始传递扭矩，系统不会产生滑动摩擦和冲击，只需控制奇数挡和偶数挡离合器执行机构使2个离合器尽快到达Kisspoint点压力即可，此阶段发动机为怠速状态。

b.t0～t1阶段，为双离合器联合起步转速跟踪阶段。此阶段非线性三步控制方法输出的期望力矩为奇数挡和偶数挡离合器期望输出力矩之和。为了平衡2个离合器的滑摩功，根据设定的规则将期望总传递力矩分配到2 个离合器上，直至(Tc1+Tc2)达到某一期望区域内，变速器可较稳定地输出一定力矩，起步过程进入下一阶段。该阶段发动机为转速控制模式，发动机输出扭矩随整车负载变化而变化。

c.t1～t2阶段，为单离合器大滑摩起步转速跟踪阶段。该阶段的工作离合器可以是1 挡离合器或2 挡离合器，如图2a、图2b 所示。工作离合器的选择以及期望的车速变化曲线可考虑驾驶员意图[10]，与进入该阶段时的油门踏板开度β0相关。设βsp为油门踏板开度阈值，可通过整车性能定义标定得到，当β0>βsp时，期望加速性能更优，选择1 挡大滑摩速度跟踪模式，当β0≤βsp时，采用2挡大滑摩速度跟踪模式。此阶段应控制工作离合器输出力矩尽可能达到非线性三步控制方法输出的期望力矩，非工作离合器在此阶段开始快速分离至Kisspoint 点以下，使其转矩尽快降低，不干涉工作离合器的接合过程。该阶段中，发动机同样处于转速控制模式，即给定发动机期望转速曲线，在规定的时间内，令发动机转速平稳增加至与期望车速对应的工作离合器从动盘转速相近的速度，以保证平稳过渡至微滑摩行驶阶段（t2以后）。

需要说明的是，期望车速曲线的选择需要符合实际，若期望车速上升过快，负载转矩将快速增大，造成发动机转速被突然“拖”低，甚至降至怠速转速以下的情况，这会引起较大的起步冲击或者发动机熄火现象。

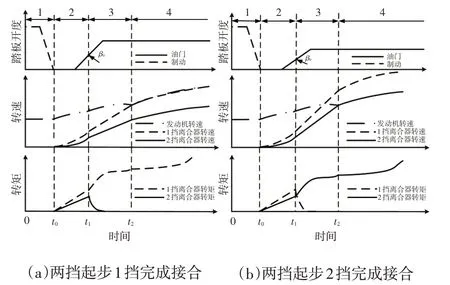
图2 DCT起步过程

d.微滑摩行驶阶段，一般采用转速PI反馈控制即可达到较好控制效果，即设置离合器和发动机期望转速差为Δωsp，离合器压力通过PI 闭环跟踪Δωsp得到，发动机通过驾驶员油门踏板开度控制。

3.2 非线性三步法车速跟踪控制器设计

基于对DCT 起步过程的动力学分析，本文采用一种非线性三步控制方法获得离合器期望转矩。

起步过程可通过车速的变化来直观表示，而车速和车轮转速近似关系为：

已知期望车速可推算出期望车轮转速，故依据车轮处的动力学特性进行控制器模型搭建。平直路面上，轮胎动力学方程可表示为：

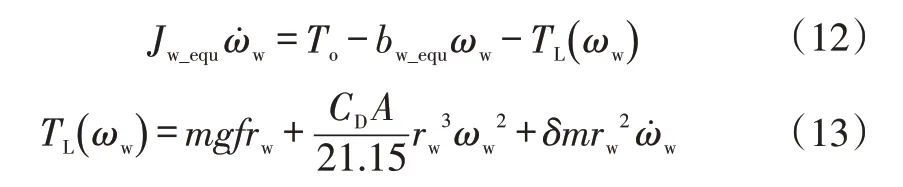
为了便于控制器设计，可求得：

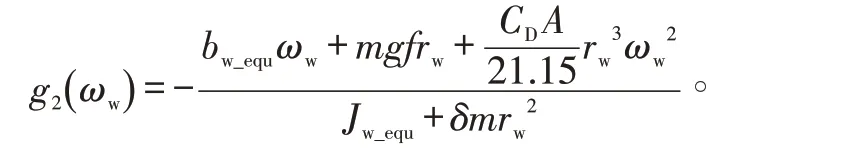
定义系统控制输入为u=To，系统状态和输出均为车轮转速，即x=y=ωw。通过设计非线性转速跟踪控制器使得起步系统输出y也就是车轮转速，跟踪期望车轮转速曲线y*，实现起步过程控制目标。

为了快速获得控制响应，基于MAP 的前馈控制方法经常在实际工程问题中采用，基于这一思想，假设系统只采用稳态控制us，系统达到稳态时，状态不再变化，即，定义系统在稳态控制u=us(ωw)下达到稳态，此时，代入式（14），可得稳态控制为：

由于汽车起步过程系统为强非线性系统，受干扰参数变化等因素的影响，跟踪目标也在实时变化，因此仅通过稳态控制并不能达到期望控制效果，引入参考动态前馈控制uf，此时u=us(ωw)+uf，将u=To代入式（14）得到：

可以看出，控制律uf与参考值的变化率相关，反映系统参考值动态变化时，系统的调节作用。由于在系统建模中无法避免建模误差，且实际系统中必然会出现扰动，通过类稳态控制和参考前馈控制，仍不能保证系统输出较好的跟踪期望值。为实现控制目标，在设计中引入反馈控制ue，充分利用反馈系统调节特性，处理系统建模误差和扰动等因素带来的影响，以达到更好的跟踪控制效果。此时，u=us(ωw)+uf+ue，定义系统跟踪误差为：

可得误差系统为：

该系统的反馈控制器可基于李雅普诺夫方法进行设计，根据工程经验，对于滞后系统，采用PI 误差反馈控制有较好的控制效果，选取李雅普诺夫函数V=e2/2+k0φ2/2，其中φ=∫edt，k0为比例控制增益系数，求导可得：

在本文的传动系统中，显然有g1≠0，可选择：

其中k1>0，得到：

式中，k1为积分控制增益系数。

此时误差系统为渐近稳定的，可以看出反馈控制ue为典型的PI控制，比例和积分控制增益是状态依赖的，可以自调节。得到系统最终的控制律形式为：

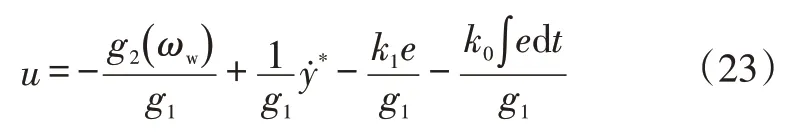
图3所示为控制律结构示意，其控制器设计过程分3 个步骤完成，同样地，控制律也由3 个部分组成，其每一部分都包含有系统的参数、状态和工况信息。综合几个部分，控制器最终达到包含系统动力学特性、系统特征参数的2个前馈控制以及包含跟踪误差的反馈控制，其结构形式简单，符合工程应用要求。

通过非线性三步法控制，可得到起步过程t0～t1阶段和t1～t2阶段的期望变速器输出力矩。

图3 控制律结构示意

3.2.1 双离合器联合起步转速跟踪阶段

由三步法实时得到期望的变速器输出目标转矩To，记作To_step2*(t)。

To确定后，需确定离合器C1、C2 承担的目标转矩Tc1_step2*(t)、Tc2_step2*(t)。根据2 个离合器磨损平衡的目标，使得期望离合器滑摩功尽可能相等，由于DCT系统中1挡和2 挡齿轮转速关系为ωc1/ωc2=i1/i2，同时此阶段轴齿摩擦和惯性的影响占比较小，通过传动效率η统一考虑，即假设力矩传递关系为效率一定的传动比关系，则离合器C1、C2的期望转矩可表示为：

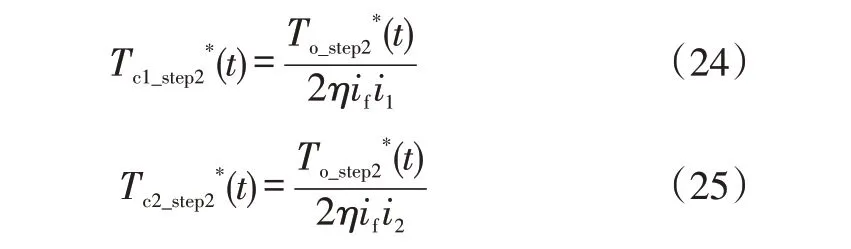
3.2.2 单离合器大滑摩起步转速跟踪阶段

在该阶段，可能为奇数挡或偶数挡离合器进行转速跟踪。需要说明的是，工作离合器通过输出期望转矩实现车速跟踪，但由于在双离合器联合起步转速跟踪阶段，2 个离合器均传递力矩，即使分离离合器马上降低压力至Kisspoint 点对应压力，由于离合器执行机构系统的迟滞特性，分离离合器力矩不会立刻减小至零，因此，工作离合器的转矩期望需要考虑此迟滞效应带来的影响。

由三步法实时得到期望的变速器输出目标转矩To，记作To_step3*(t)。以单离合器大滑摩起步转速跟踪阶段选择奇数挡离合器大滑摩速度跟踪控制为例，偶数挡离合器期望力矩Tc2_step3*(t)=0，奇数挡离合器期望力矩Tc1_step3*(t)=(To_step3*(t)-Tc2i2if)/ηifi1。

同理，可得到2挡大滑摩速度跟踪控制的离合器期望转矩。

4 DCT起步控制策略验证

在AMESim 中搭建6挡DCT 整车仿真模型，主要包括发动机、6 挡DCT、车体、悬架、轮胎、路面等，还包含离合器及其液压执行机构，其中轴齿部分建模考虑了摩擦和弹性等特性，能较真实地反映传动系的耦合和非线性特性。在MATLAB/Simulink中搭建起步控制器模型，包括起步逻辑模块、各阶段力矩控制模块、发动机控制模块、力矩-电磁阀电流转换模块。

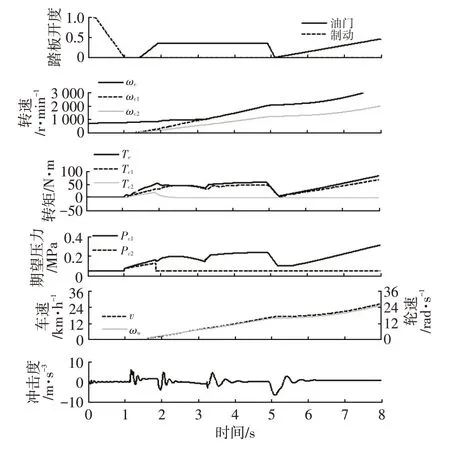
图4 两挡联合起步，1挡完成起步接合仿真结果

图4 所示为名义工况下两挡联合起步，1 挡完成最终接合的仿真（仿真1）结果。可以看出，初始制动踏板命令未达到零，汽车处于消除空行程阶段，2 个离合器期望压力为Kisspoint 点压力，第1 s 时制动踏板完全松开，起步进入双离合器联合起步转速跟踪阶段，经过控制，2 个离合器转速平稳上升，在第3.3 s 左右完成起步过程。期望压力通过三步控制法得到的期望力矩查表得到。在给定期望压力下，奇数挡和偶数挡离合器转矩先同时上升，且奇数挡离合器传递转矩较大，到第1.8 s左右，偶数挡离合器期望压力降为Kisspoint 点压力，期望力矩均由奇数挡离合器承担。实际偶数挡离合器电磁阀电流响应及液压执行系统均存在迟滞，因此偶数挡离合器力矩并未立刻降低至0，该策略可控制奇数挡离合器传递剩余期望力矩。该控制方法可实现平稳的起步过程，这里定义的起步结束状态为车速大于8 km/h，从双离合器联合起步转速跟踪阶段开始计算，本文仿真中经过2.23 s完成起步过程，且起步冲击较小，在±7 m/s3范围内。

如图5所示，选取的车轮期望转速为一条三次平滑曲线，经过非线性三步控制方法，得到实际车轮转速能很好地跟踪期望转速，跟踪误差在±0.3 rad/s 范围内。总控制输入中稳态控制律us、参考前馈uf的前馈控制占比较大，反馈控制ue占比较小，说明该方法可充分利用系统原有的动力学特性、整车参数以及可观测状态量等信息，实时给出较为合理的前馈、反馈，承担小偏差调节作用，主要处理建模误差、系统扰动等因素的影响，与工程实际应用中常见的“前馈+误差反馈”系统相比，结构形式类似，但可以充分利用系统本身的信息，从而大幅减少控制器参数标定的工作量。

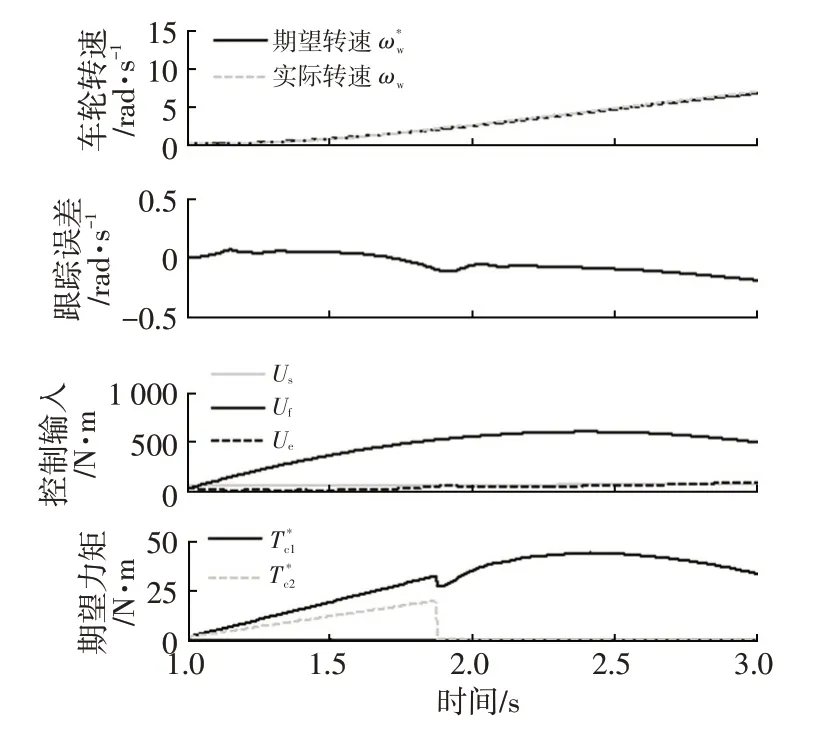
图5 仿真1控制输入及转速跟踪效果

不改变工况，仅改变期望车轮转速曲线为二次光滑抛物线，进行仿真2，控制输入及转速跟踪效果如图6所示，可以看到，跟踪曲线改变后，该控制器仍可实现良好跟踪控制效果，跟踪误差在±0.2 rad/s范围内，且在该转速期望曲线下，双离合器联合起步转速跟踪阶段占用时间较长，双离合器滑摩功平衡效果更显著。

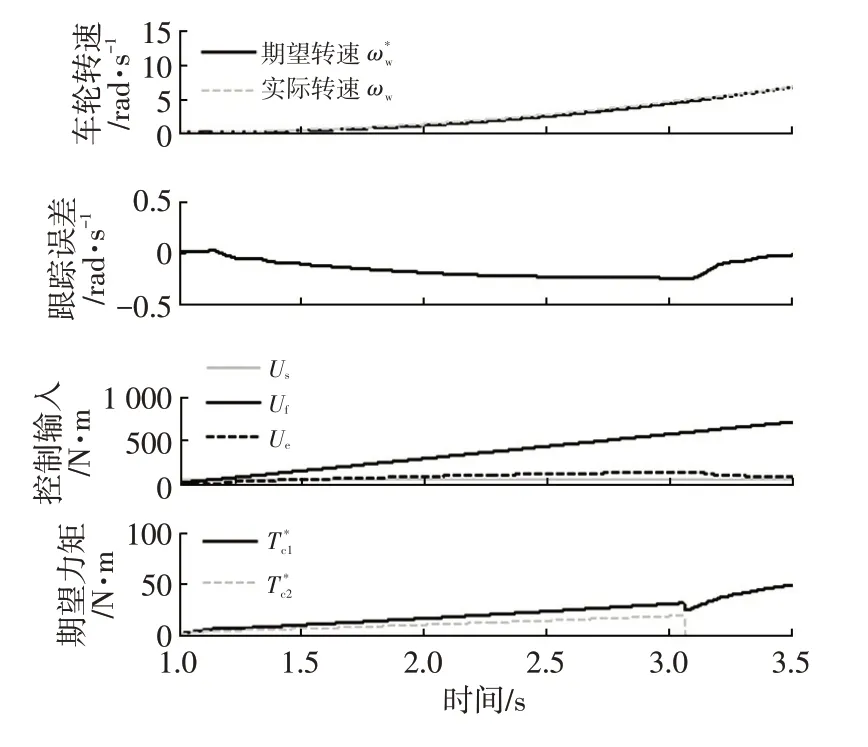
图6 仿真2控制输入及转速跟踪效果

类似地，当驾驶员加速需求较小或者地面湿滑时，选择两挡联合起步2 挡完成结合。图7 所示为名义工况下两挡联合起步，2 挡完成最终接合的仿真（仿真3）结果。由图7可知，采用的期望轮速曲线为三次平滑曲线，同样地，可以实现两挡起步，2 挡完成接合。由于2挡传动比较小，且发动机转速需要保证高于怠速状态下的转速以避免发动机熄火，因此在2 挡起步控制过程中，起步期望的车轮转速也较1 挡起步更大，需要更长的起步时间。本次仿真定义的起步完成标志为车速大于12 km/h。在给定期望压力下，奇数挡和偶数挡离合器转矩先同时上升，且奇数挡离合器传递转矩较大，到第1.8 s 左右，奇数挡离合器期望压力降为Kisspoint 点压力，期望力矩均由偶数挡离合器承担；在1.8～4.3 s 左右，偶数挡离合器传递剩余期望力矩，完成起步过程。在整个起步过程中，冲击度均在±8 m/s3范围内，起步平顺性好，满足控制需求。

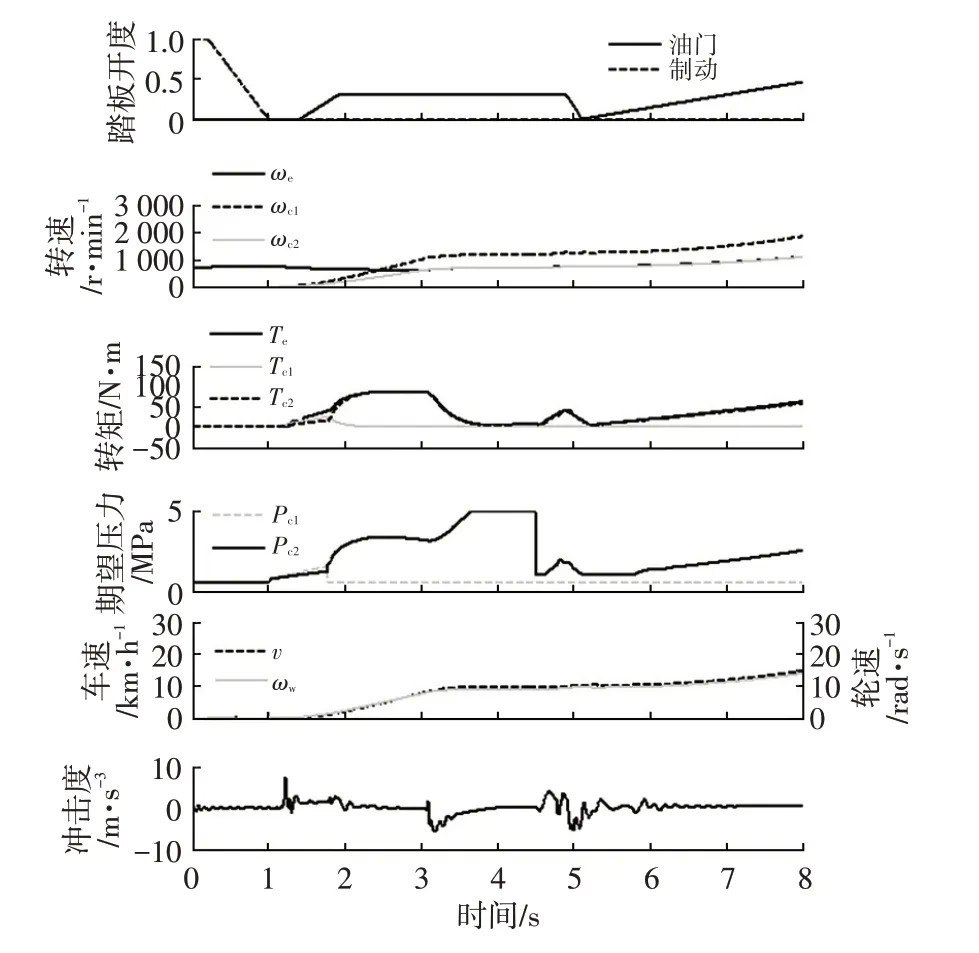
图7 两挡联合起步，2挡完成接合仿真结果

表1 所示为3 组仿真离合器单位面积滑摩功，仿真1 和仿真2 滑摩时间短，故滑摩功较小，且奇数挡、偶数挡离合器都承担了起步过程中的滑摩。仿真3 由于2挡起步需要的时间较长，因此滑摩功较1 挡最终完成起步更大，均满足每次接合过程单位面积滑摩功小于0.4 J/mm2的控制需求。

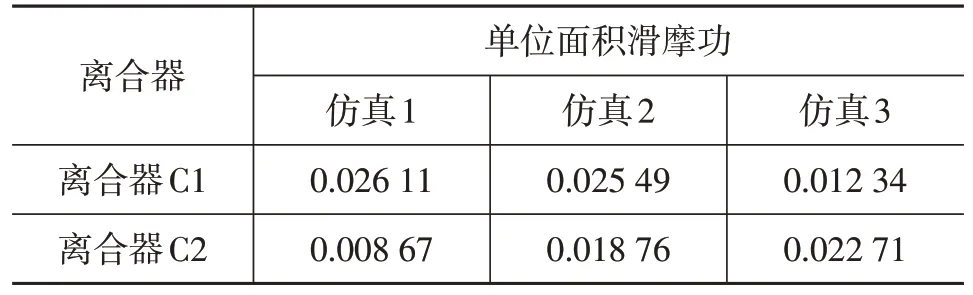
表1 仿真离合器单位面积滑摩功J/mm2

5 结束语

基于双离合器自动变速器的结构特点，本文提出了双离合器自动变速器两挡联合起步的控制策略，控制器结构与常用工程实现结构一致，且具有增益状态依赖的自调节能力，搭建装备双离合器自动变速器的车辆仿真模型对起步控制策略进行了验证。仿真结果表明，提出的两挡起步控制策略可很好地实现车轮转速跟踪，在达到较好起步效果的同时可有效平衡离合器磨损。