串并联式机电耦合系统方案设计及寻优分析＊

赵江灵 徐向阳 祁宏钟 朱永明 董鹏

（1.广州汽车集团股份有限公司汽车工程研究院，广州 511434；2.北京航空航天大学，北京 100191）

主题词：混合动力系统 串并联式机电耦合系统 最优构型 动态寻优

1 前言

在混合动力汽车方案上，日本主要采用功率分流和串并联技术路线，美国主要采用功率分流技术路线，欧洲主要采用P2 技术路线，中国主要采用串并联技术路线。欧阳明高和徐向阳等对混合动力传动技术路线进行了分析[1-2]；韩兵、秦大同等对混合动力关键技术、控制策略等进行了较为深入的研究[3-9]；广汽集团也开发了串并联类型的混合动力机电耦合产品[10-13]。

本文首先建立串并联的基础构型和方案评价体系，然后基于某车型的动力性与经济性目标，通过仿真分析，确定串并联类型的机电耦合系统的发动机及驱动电机的最佳挡位数量、最优速比、最佳电机参数等，并基于仿真结果开展机电耦合系统的构型设计。针对所设计的机电耦合系统，进行动态规划分析，探寻最优模式划分方法和系统控制方法。对动态规划的模型进行优化，缩短仿真时长，针对所设计的系统，在优选范围内再进行速比寻优，进一步优化系统参数。

2 系统方案寻优

2.1 基础构型定义

如图1所示，本文混合动力系统的基础构型采用串并联方案，发电机通过一级定轴齿轮实现增速降扭，以降低驱动电机的扭矩需求。

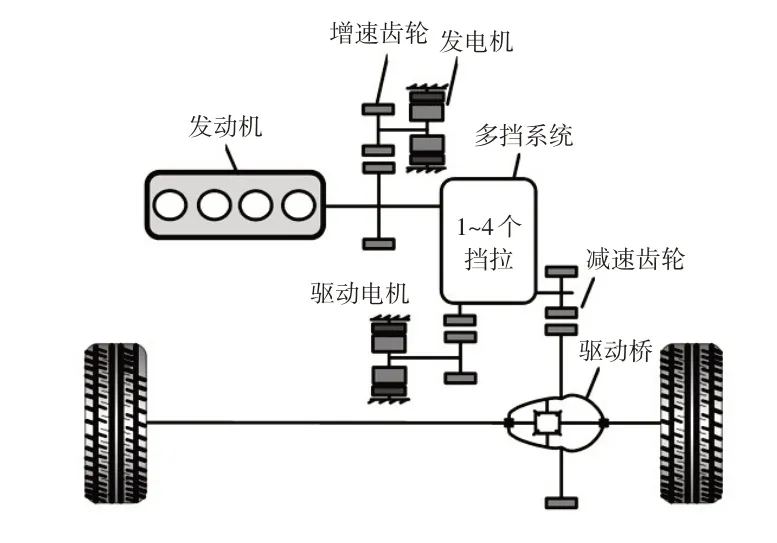
图1 串并联混合动力方案基础构型

系统具备单电机纯电动模式、双电机纯电动模式、驱动电机1～2个挡位、发动机单独驱动1～4个挡位、1个增程模式。

2.2 串并联构型方案寻优

该方案发动机有4 个可选挡位，驱动电机有2 个可选挡位，共8 种组合，需针对每种组合进行优化。表1 所示为发动机2 个挡位、驱动电机1 个挡位时的寻优设置。首先确认串并联方案发动机和驱动电机的最优挡位数量，再确认不同挡位下的最优速比和最优电机参数。

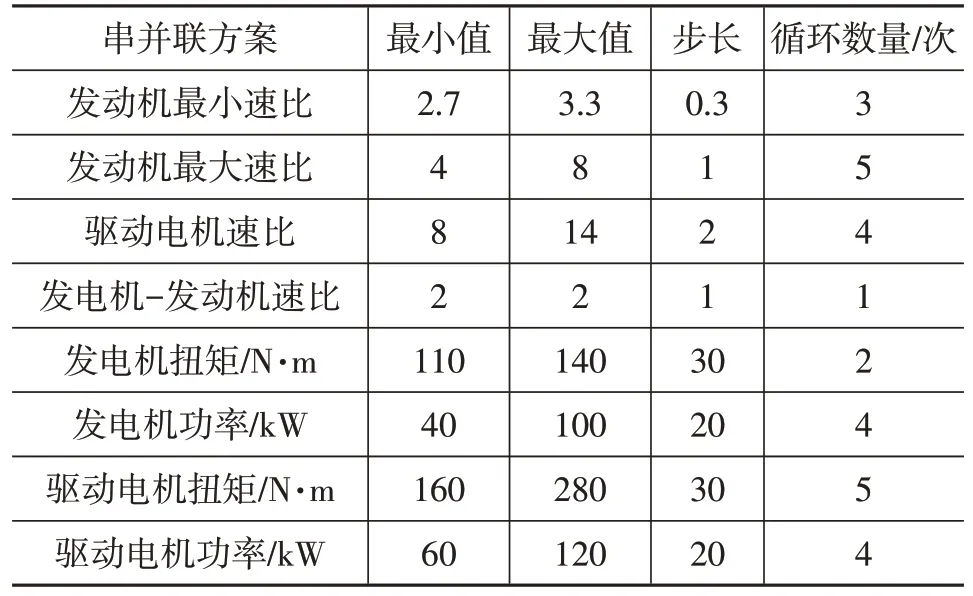
表1 串并联方案寻优设置

为了更好地评价机电耦合系统的优劣，本文建立了概念方案评价标准，如表2所示，主要分为动力性能、经济性能和成本（电机和电机控制器），权重分别为25%、40%和35%。该阶段仅分析不同类型的方案和不同挡位组合对系统的影响，因此暂未考虑零部件加工难度、控制复杂程度、布置包络等因素的影响。

对动力性能按照最高车速、加速时间、最大爬坡度进行拆分，并赋予不同的权重；对全球统一轻型车辆测试循环（Worldwide Light-duty Test Cycle，WLTC）和新欧洲行驶循环（New European Driving Cycle，NEDC）工况的油耗、电耗及定速油耗进行拆分，并赋予不同的权重；因现阶段多挡方案的具体实现方式未知，无法估算传动系统的成本，所以暂时只考虑电机和电机控制器的成本。

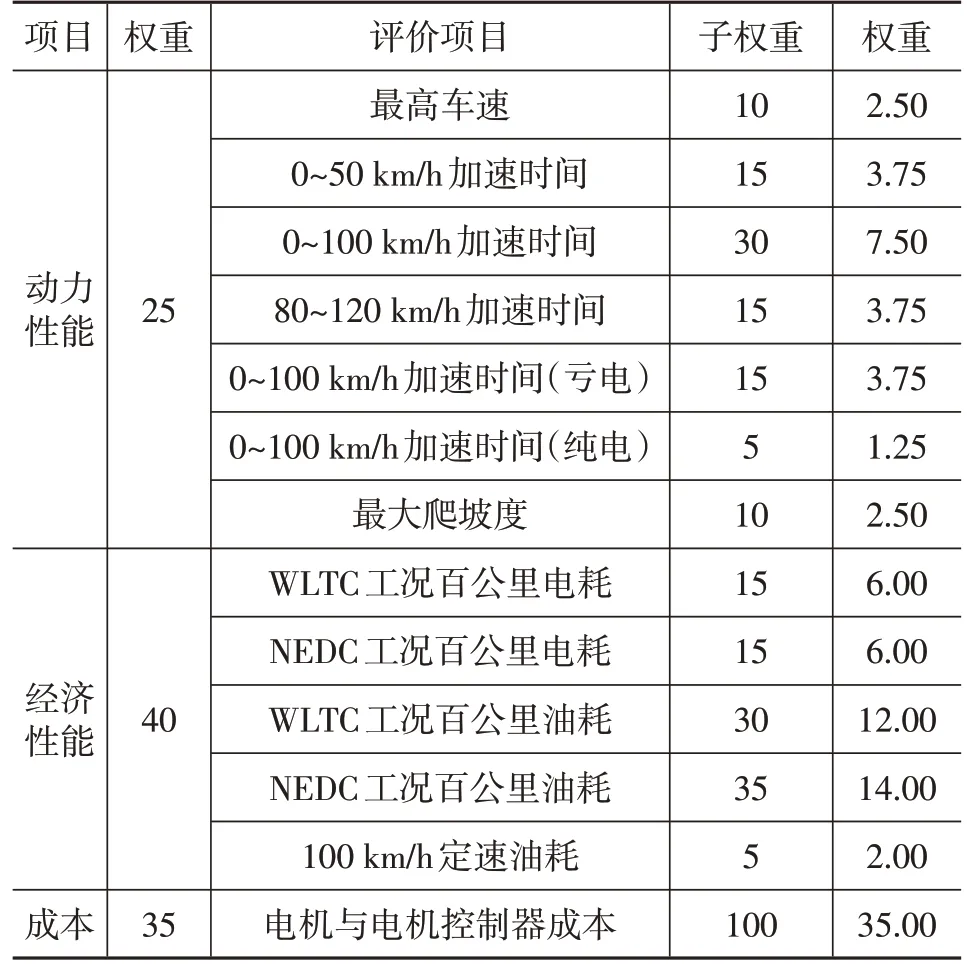
表2 概念方案评价标准 %

根据表2定义的评价标准，串并联的前10位的仿真结果如图2所示。

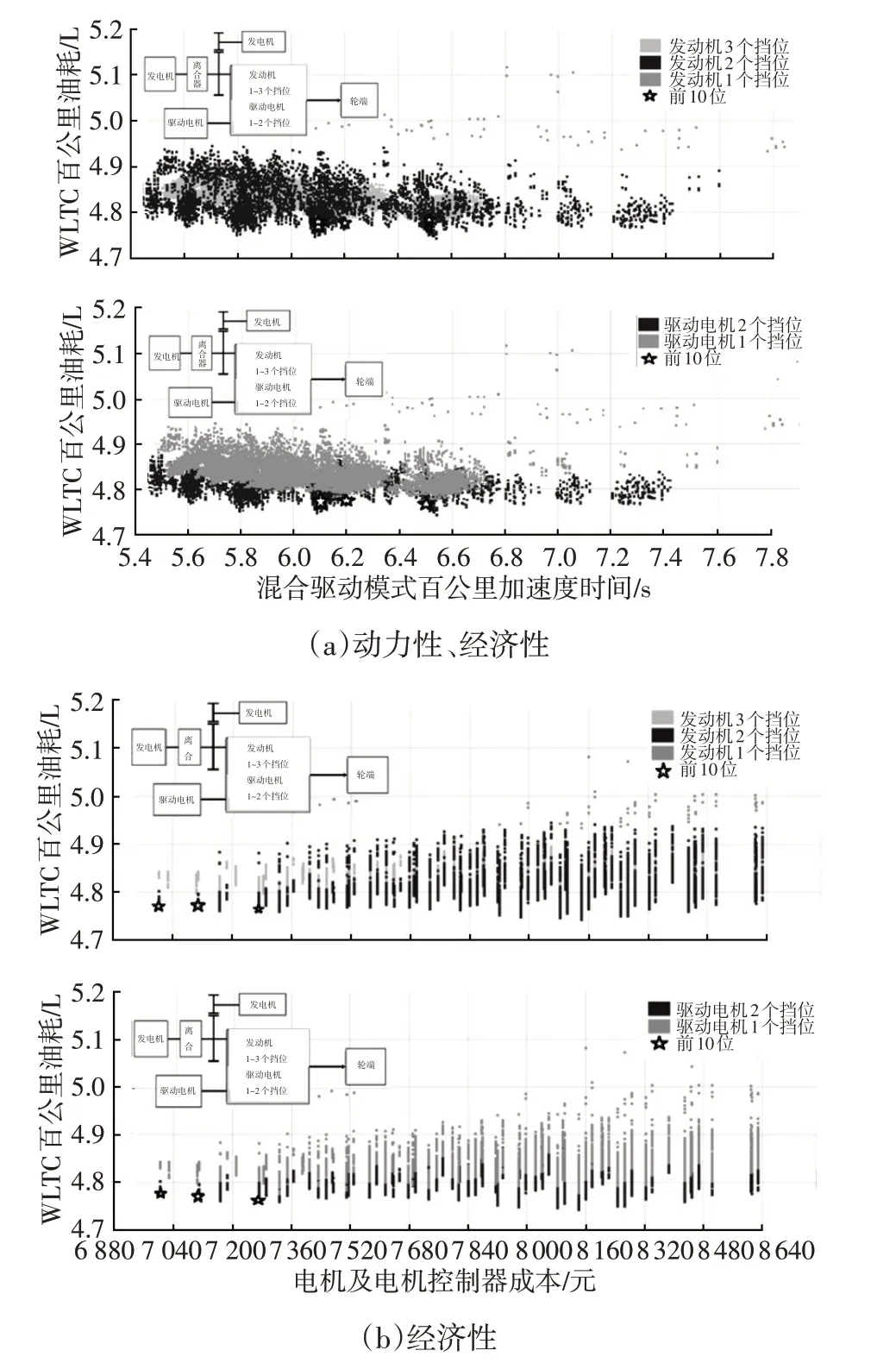
图2 串并联基础构型不同方案性能对比

通过以上分析可知：

a.对于串并联混合动力系统，最优的方案为发动机2个挡位，驱动电机2个挡位；

b.最优方案中发动机的1挡速比约为5，2挡速比约为3，驱动电机的1挡速比约为12，2挡速比约为8；

c.匹配发电机的需求功率为60 kW，扭矩为

120 N·m，驱动电机的需求功率为60 kW，扭矩为200 N·m；

d.分析电机挡位对动力性和经济性的敏感性，发现电机的挡位对经济性影响不大，2 挡比1 挡百公里燃油消耗量降低0.05 L；

e.综合考虑动力性、经济性、电机和电机控制器的成本因素，发动机2 个挡位、驱动电机1 个挡位方案更优。

3 机电耦合系统方案设计

发动机2个挡位可以通过同步器多挡化方案、双离合式多挡化方案、行星齿轮多挡化方案实现。

综合动力性能、经济性能、控制难度、包络空间、零部件加工难易度、速比灵活性、NVH 性能、壳体加工难度、成本（含传动系统）、混合动力系统总质量等因素，确认机电耦合系统方案原理如图3 所示，布置如图4 所示。

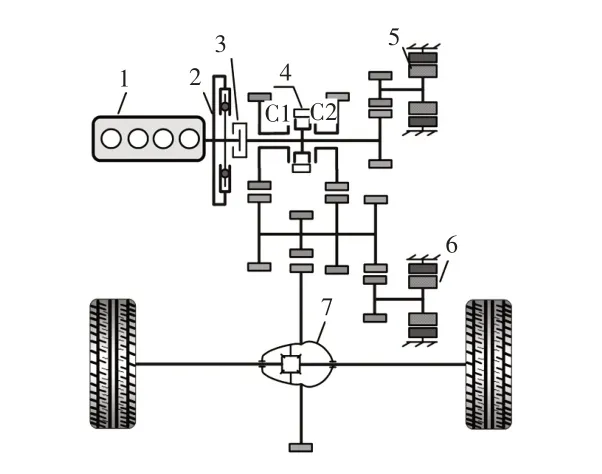
图3 机电耦合系统原理

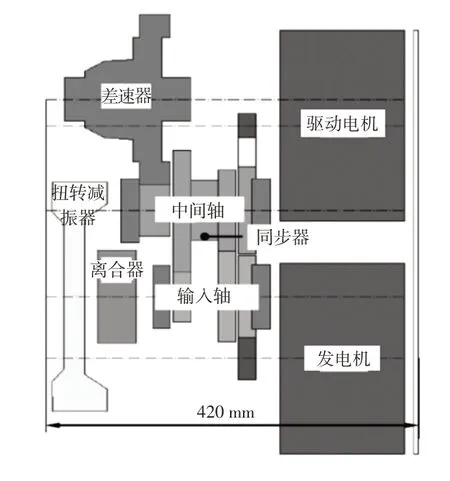
图4 机电耦合系统布置

机电耦合系统可实现发动机、发电机、驱动电机动力耦合的功能，同时具备不同工作模式，如表3所示。

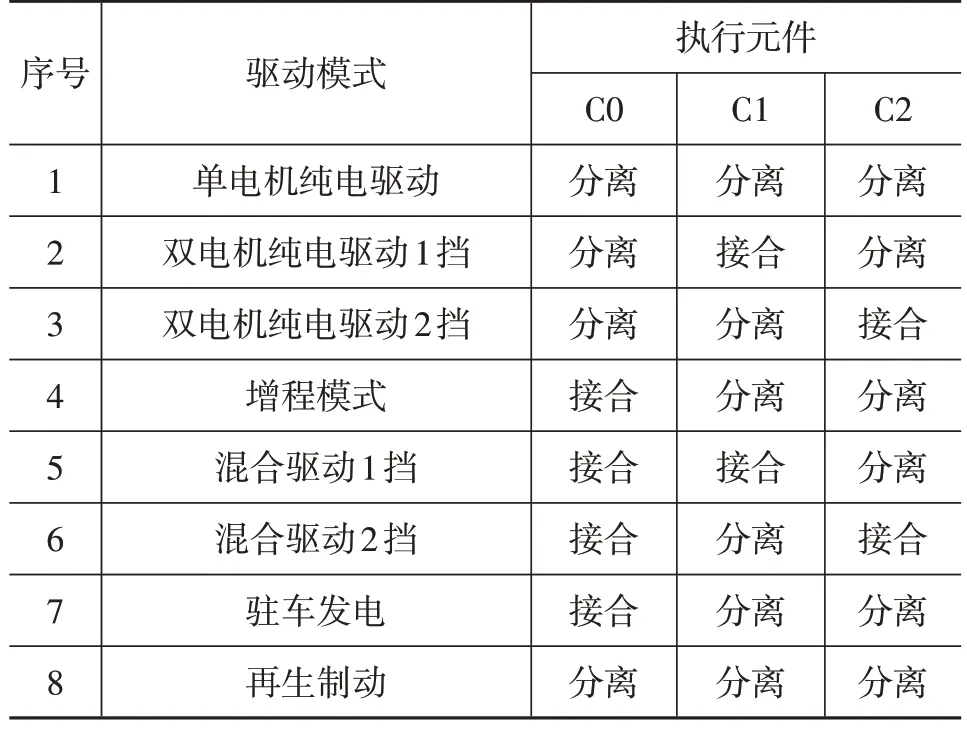
表3 可实现的工作模式

4 动态寻优

4.1 机电耦合系统动态寻优分析

动态规划算法是一种求解多阶段决策问题的方法，混合动力汽车的燃油经济性优化问题也可以建立成一个多阶段决策问题。首先将循环工况按时间划分为N个阶段（即离散化），这些阶段相互联系，在每个阶段都对能量分配作出决策，该决策不仅影响本阶段的代价函数值，还决定了下一阶段的初始状态，每个阶段的决策构成一个决策序列，最后通过正向寻优的方法得到该工况下的最优决策方案。可以看出，动态规划算法结果的精度取决于变量的离散程度，离散点越多，结果越接近理想最优，但是运算量也大幅增加，耗时加长。这些条件均限制了动态规划算法在实车上的应用，但是动态规划全局优化算法求得的分配策略为理论最优解，故目前主要作为评价其他控制策略和设计其他控制策略的参考而存在[14]。

本文基于该构型，使用动态规划的策略，寻求最优解决方案。如图5 所示，动态规划逆向计算递推过程[14]为：

a.以荷电状态（State Of Charge，SOC）为状态变量、发动机转速wICE、发电机扭矩TEM1、驱动电机扭矩TEM2、模式4个参数为决策变量，对每种途径都进行仿真计算，同时计算“代价函数”，即燃油消耗率、模式间切换的惩罚值、SOC变换的惩罚值三者之和；

b.找到最优的“代价函数”，提取每一步的决策变量值，形成一个N×4的矩阵（N步、4个变量）；

c.根据最优决策变量的矩阵仿真计算油耗。

动态规划算法的优化目标为给定循环工况下的燃油经济性最佳，循环工况划分步长为1 s，从而将混合动力汽车能量分配最优决策问题转换成为一个N阶段决策问题[14]。在动态规划的仿真程序中，根据系统的多种工作模式以及动力源的不同工作点等组成的变量，使得系统在不同的工况点存在多个选择。通过动态规划程序，首先找到代价函数最小的路径，如图6 所示，并记录下每个步骤的状态，再正向求解该工况的经济性。图6 中，路径旁的数字表示相应路径的代价函数值。

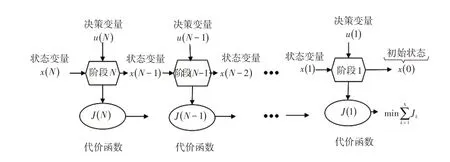
图5 动态规划算法逆向求解过程

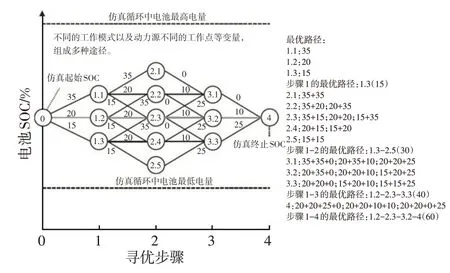
图6 动态规划最优路径说明

4.1.1 单电机纯电动模式

在单电机纯电动模式下，驱动电机EM2驱动，发动机和发电机EM1 均不工作。根据工况，可以推导出各动力源的动力学关系：

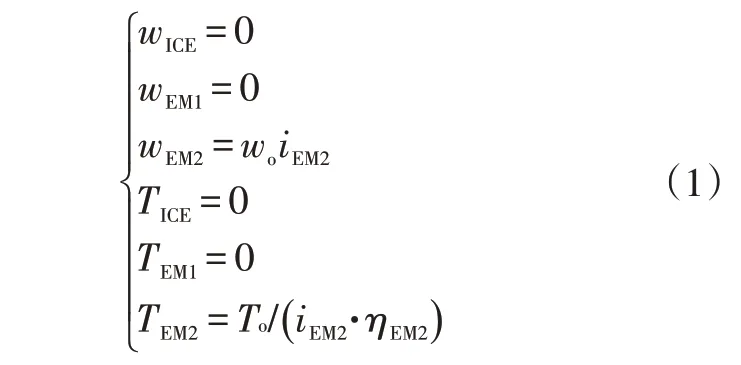
式中，wICE、wEM1、wEM2分别为发动机转速、发电机转速、驱动电机转速；wo为轮端需求转速；iEM2为驱动电机到轮端的速比；TICE、TEM1、TEM2分别为发动机扭矩、发电机扭矩、驱动电机扭矩；To为轮端需求扭矩；ηEM2为驱动电机到轮端的机械传动效率。

4.1.2 双电机纯电动模式

在双电机纯电动模式下，发电机EM1 与驱动电机EM2同时驱动，发动机不工作。该模式下，轮端需求先通过驱动电机EM2满足，如果不能满足需求，则通过发电机EM1 补偿。根据工况，可以推导出各动力源的动力学关系：

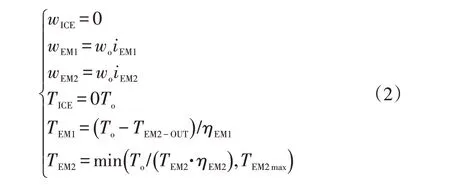
式中，iEM1为发电机到轮端的速比；TEM2-OUT为驱动电机输出到轮端的扭矩；ηEM1为发电机到轮端的机械传动效率；TEM2max为驱动电机的峰值扭矩。

4.1.3 混动模式

在混动模式下，发动机、发电机EM1 与驱动电机EM2 同时工作。该模式下，发动机和驱动电机EM2 的扭矩为寻优变量，需在全局范围内对发动机和驱动电机EM2的扭矩进行寻优，根据工况，可以推导出各动力源的动力学关系：

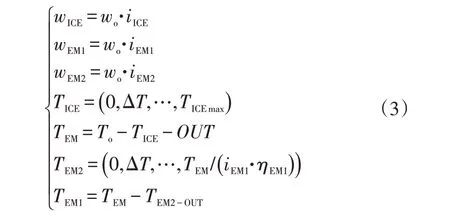
式中，ΔT为发动机扭矩和驱动电机扭矩的寻优步长。

混合驱动1 挡与混合驱动2 挡的优化原理相同，仅速比有区别。

4.1.4 串联增程模式

在串联增程模式下，发动机带动发电机EM1，驱动电机EM2驱动，发动机的转速和扭矩都是寻优变量，需要在发动机的转速和扭矩范围内寻找最优工作点。根据工况，可以推导出各动力源的动力学关系：

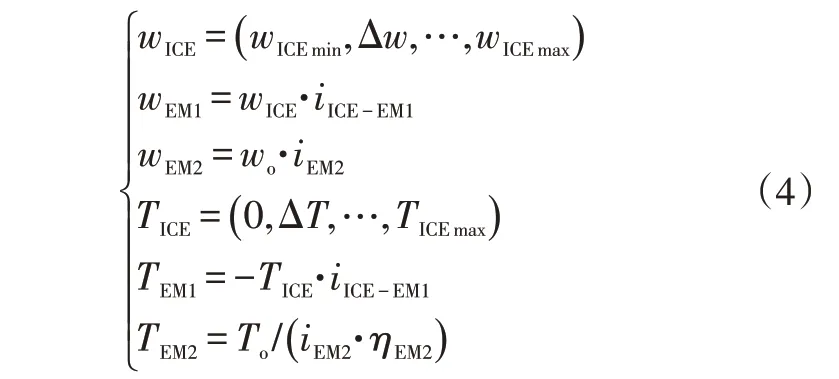
式中，wICEmin、wICEmax分别为发动机的最小、最大转速；Δw为发动机转速的寻优步长。

针对动态规划仿真时间长、模式切换次数多、发动机起动和停机频繁、工作点离散的问题，提出了设置模式切换惩罚矩阵的方法，以提高仿真效率。双电机纯电动2 挡多用于高速工况，而在寻优过程中，大多使用NEDC、WLTC、中国轻型汽车行驶工况（China Lightduty Vehicle Test Cycle，CLTC），不存在高速纯电动工况，为了减少寻优时间，在动态规划中未考虑双电机纯电动2 挡模式。设模式1～5 分别表示单电机纯电动模式、双电机纯电动模式、混合驱动1 挡模式、混合驱动2挡模式、串联增程模式。惩罚矩阵如表4 所示，各模式之间相互切换均对应相应的惩罚值，因模式不同，惩罚值也有差异。其中：Mmn为模式m与模式n间切换的惩罚值；Estr为起动发动机的惩罚值，在纯电动向混合驱动及增程模式切换时，需要起动发动机，故代价函数中需增加该惩罚值；Estp为发动机停机的惩罚值，在混合驱动、串联增程向纯电动模式切换时，发动机需要停机，故代价函数中需增加该惩罚值。

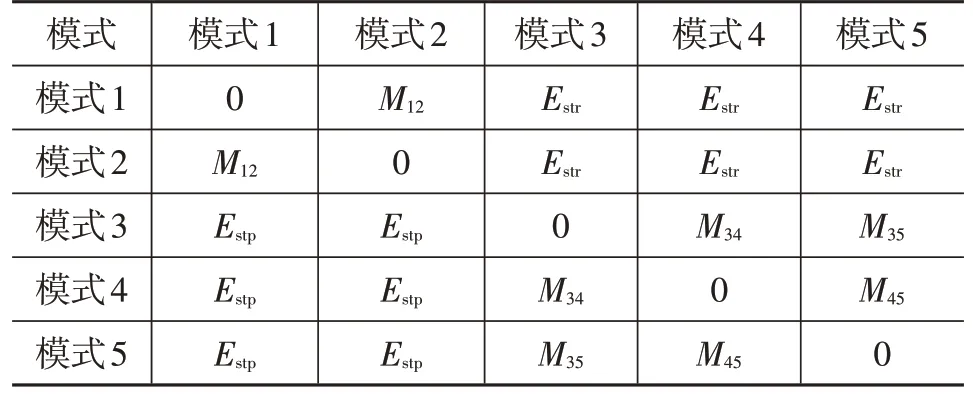
表4 模式切换惩罚矩阵

4.2 机电耦合系统动态寻优结果

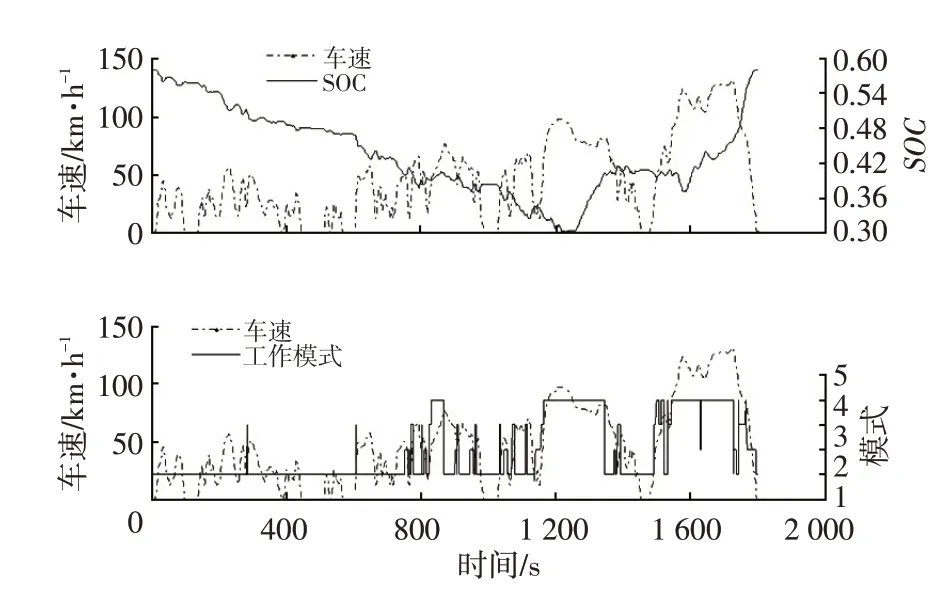
图7 WLTC工况SOC与模式变化情况

图7 所示为WLTC 工况下动态寻优过程中SOC 的变化情况及模式运行情况，由仿真结果可知，随着工况变化、整车轮端需求的变化，需要适时选择单电机纯电动、混合驱动1挡、混合驱动2挡、串联增程模式。在低速阶段，多采用单电机纯电动模式，在高速阶段多采用混合驱动2挡模式。

图8 所示为WLTC 工况下发动机、发电机、驱动电机的转速、扭矩变化情况。不同工作模式的工作点如图9 所示，低速段多采用单电机纯电动模式和增程模式，中高速、大扭矩需求时，多采用混合驱动1 挡模式，高速、中小扭矩需求时，多采用混合驱动2 挡模式。对于制动回收可用单电机回收和双电机回收两种模式，尽量多回收制动的能量。

图10 所示为发动机、发电机、驱动电机的工作点。可知，在WLTC 工况下，各动力源的工作点均处于效率较优处。

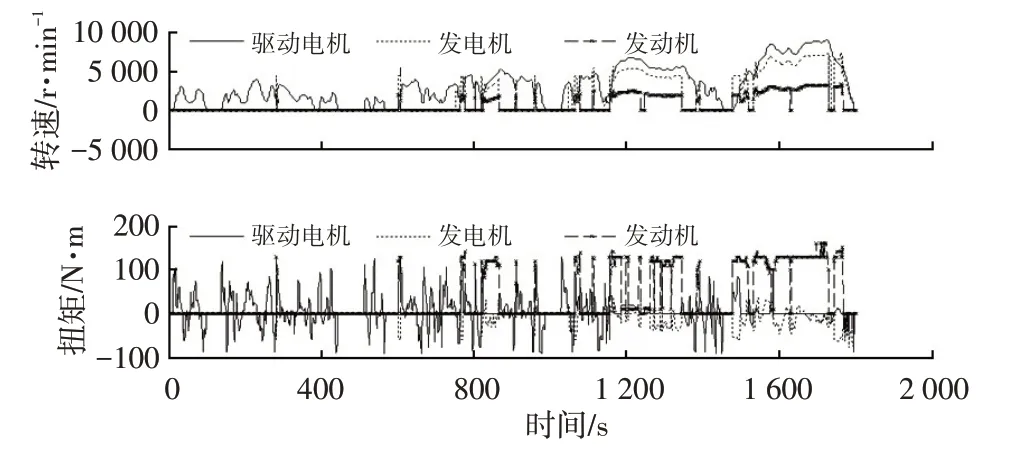
图8 动态寻优各动力源转速扭矩信息

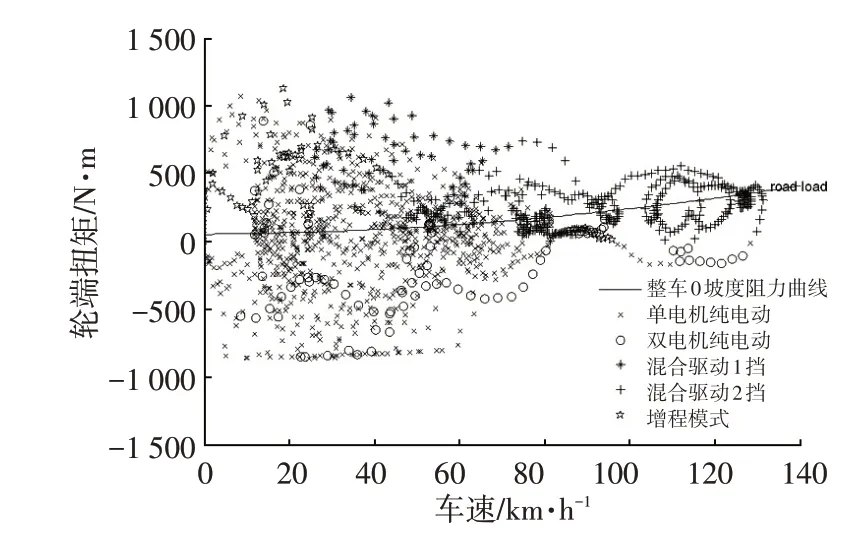
图9 不同工作模式的工作点

图10 各动力源工作点

通过动态规划仿真程序对各速比进行寻优。驱动电机速比与发动机1挡、2挡速比寻优结果分别如图11、图12所示。根据仿真优化分析，发动机1挡最优速比约为4.8，发动机2挡最优速比约为3.1，驱动电机最优速比约为9。

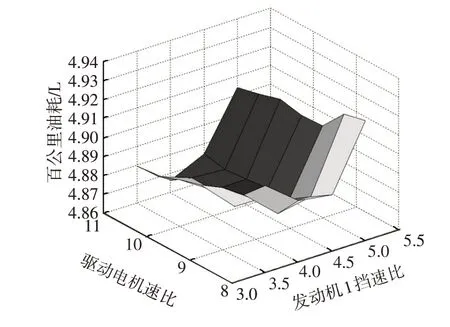
图11 驱动电机速比与发动机1挡速比寻优

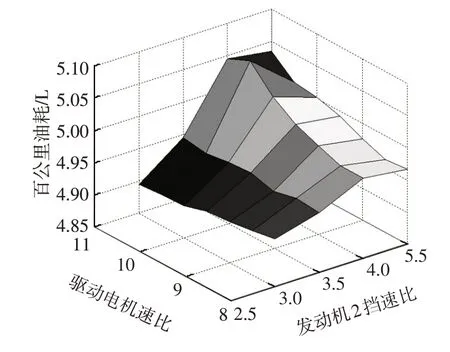
图12 驱动电机速比与发动机2挡速比寻优

5 结束语

本文介绍了一种新型机电耦合系统方案，优化了发动机的挡位、增加了双电机纯电动模式、优化了发动机与发电机的连接关系、提高了机电耦合系统的集成度并提升了系统的效率，实现了整车动力性能和经济性能的改善。针对该新型机电耦合系统进行了动态规划寻优分析，分析了理论最优的模式划分方法，可为实际的模式划分控制策略提供参考。