基于交叉组合因子分析的主观评价尺度一致性仿真研究

杨万安 李小龙 刘红军

（泛亚汽车技术中心有限公司，上海 201201）

主题词：车辆动力学 主观评价 交叉分组因子分析 尺度一致性指标 随机扰动

1 前言

在整车开发过程中，主观评价常用于车辆动力学、整车NVH、座椅舒适性、外观质量等的评价。在主观评价过程中，评价的客观性必须得到保证，即评价者应保持评价标准的客观性。由于个人对被评价对象特性的偏好难以定量描述，目前没有量化指标可较好地描述主观评价时所依据的内在评价尺度，因此很难对评价数据进行合理筛选，进而剔除质量不高的样本。对于主观评价质量的研究一般分为3个方面：

a.主观评价与客观测量的一致性。在主观评价的同时进行客观测量，构造出适合的指标，使其与主观评价的结果有较好的一致性[1-6]。

b.主观评价团队成员之间的一致性。团队成员评价偏好的统一，可通过评价方法优化、严格评价过程、提升个人经验等来实现。实际分析中，常使用层次分析法中的一致性检验及其改进方法来检验评价的准确性[7-8]，在样本较多时也通过成对比较法来减少主观误判[9-10]，或者探索在评价结果不一致的情况下更好的决策方法[11-14]。

c.主观评价中个人评价的一致性。目前相关研究非常缺乏，少量研究多是针对评价者的评价结果进行统计分析，试图找到背后的影响因素[15]。

只有在个人评价尺度稳定的前提下，才能真正实现团队成员之间的一致性。本文利用交叉分组因子分析法构造反映评价者内在尺度一致性的指标，并进行仿真分析，研究其普适性[16]。

2 评价尺度一致性指标

2.1 因子分析法与评价尺度

因子分析法的主要步骤是：假设样本数量为m、维度为n的原始数据标准化后的数据矩阵X由公共因子F和特殊因子ε构成，即X=A×F+ε，其中A为因子载荷矩阵；利用主成分分析法对其相关系数矩阵XTX求解特征方程，可得到n个特征根λ及其特征向量β。

变量缩减过程以λ为依据，保留所有λ>1 的因子。另一种常用的依据是根据因子的累计方差贡献率来确定适合的因子数，保留的数据方差信息>85%。

因子分析结果中的一个重要内容为因子载荷矩阵，或相应的因子载荷分布图，它反映了各数据变量在新的因子维度中的相互影响程度。针对以往大量车辆动力学性能主观评价数据的分析表明，第1个、第2个因子的累计方差贡献率超过85%，其余各因子累计方差之和明显小于前2个，因此，只用2个因子即可解释绝大部分评价变量的方差。

根据上述初步分析，构造一个二维的因子载荷分布图，其中X、Y轴分别为第1、第2因子载荷，每个变量（即评价指标）所对应的第1、第2因子载荷得分在图中表现为一个点，各变量的载荷得分点（即图中各点）之间的相对位置则反映了评价者对各变量间相互关系的主观认知，即彼此间的夹角包含了评价尺度的重要信息，可以用来反映个人内在的评价尺度，由对各变量点间夹角αi,i+1(i＝1,2,3,…,n)变化的观察进行量化表征。

2.2 交叉组合法及一致性指标

基于上述概念，本文提出一个可以有效观察到个人在进行主观评价时自身评价尺度波动的方法，即交叉组合法。首先对车辆动力学主观评价的原始数据进行交叉重组，再分别用因子分析得到相应的因子载荷分布图，并利用其中各变量点夹角的统计结果形成有效观察评价尺度波动的量化指标。

对于样本数量为m、评价项目数量为n的某评价者原始评价数据，标准化后的数据矩阵为m×n的矩阵X，交叉组合分析的具体步骤为：

a.从中依次去除1个样本，形成交叉分组，如图1所示。每个交叉分组数据为样本数量为(m-1)、评价项目数量仍为n的数据子矩阵X1、X2、…、Xm。

b.针对由原始数据交叉组成的子矩阵进行因子分析，得到相应的因子载荷分布图。

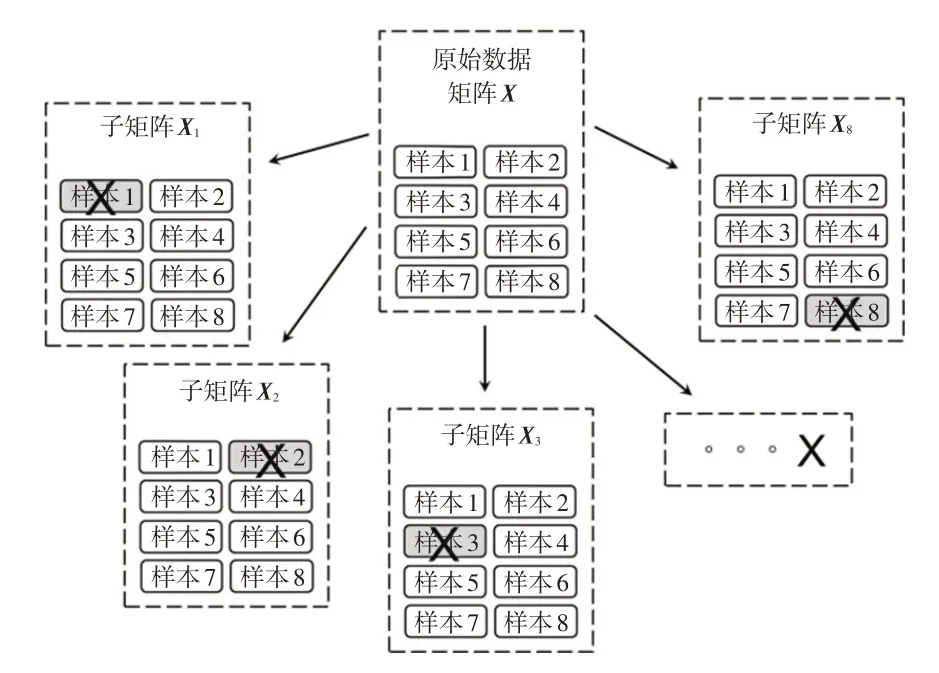
图1 原始数据的交叉组合（以8个样本为例）

c.构造出可以反映主观评价尺度波动程度的尺度一致性指标（Scale Consistency Index，SCI）。

设α(i,i+1),j为第j个数据子矩阵Xj在进行因子分析后得到的第i个和第(i+1)个变量点之间的夹角，St(αi,i+1)为全部交叉分组分析中第i个和第(i+1)个变量点之间共计m个夹角的标准差。

主观评价的尺度一致性指标可定义为：

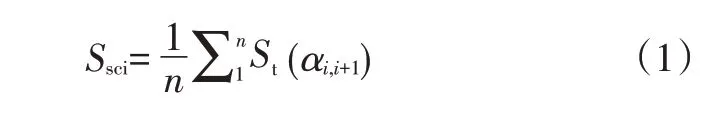
这样，评价者的主观评价尺度一致性由其评价数据构成的交叉分组因子分析结果体现，可反映评价者对评价变量感知尺度的量化波动。较大的尺度一致性指标反映了评价者感知尺度的波动较大，说明评价者在内、外干扰影响下的主观评价偏差较大，可信度降低。反之，评价结果可信度较高。

3 评价尺度扰动仿真

为验证基于交叉分组因子法的主观评价尺度一致性指标的有效性和普适性，利用仿真过程研究多个因素对SCI的影响程度。

主观评价的影响因子一般有多个，为简化仿真分析的难度，以车辆动力学性能的主观评价为研究对象，构造了由2个因子控制的数据作为研究的基准数据。

构造代表主观评价数据标准化后的样本数量为m、变量数量为n的矩阵X，其因子载荷矩阵为A，公共因子为F，即：

为了方便研究，构造的各变量均仅受控于2个因子F1、F2，X模拟了一位极其优秀的主观评价者的精准评分，控制评价结果的各因子载荷不变，由其得到的相应评价尺度保持高度一致，也即对各样本的每个变量均保持相同的评价尺度。

在真实的主观评价活动中，评价者常因各种内在或外在影响因素产生评价尺度的波动，用相应的随机矩阵ε、ε′代表这2种因素，最终的评价结果可表示为：

式中，ε为评价者因对某些样本先入为主或存在偏见而产生评价尺度波动带来的偏差，可作用于某个或多个样本；ε′为评价者因自身技术水平或情绪波动引起的在某个或多个评价项目上的偏差。

本文从多个方面对SCI 的有效性和普适性进行仿真研究。

3.1 尺度一致性指标的统计计算

正常评价过程中，ε和ε′的变化可能导致Ssci的提高，但也可能因此使其得到改善。

为了避免其中的不确定性，采用统计方法，以大量随机偏差扰动下尺度一致性指标计算样本的平均值代表在该偏差扰动下相应的尺度一致性指标，而且每个模拟计算过程中均会随机构造出新的样本矩阵，以使统计过程更具随机性和代表性。

随机偏差扰动的大小根据主观评价的实际情况确定。本文以车辆动力学主观评价过程为例，在10分制中大部分被评价车辆的性能得分在6.5～8.5 分之间，故设定扰动范围为±1分，在此基础上叠加±0.25分的随机量。

以随机生成10 个样本、8 个评价项目的两因子评分矩阵为例，初步的研究表明，以将随机扰动加载到某原始数据矩阵中的第3 个和第7 个样本上为例进行模拟计算。当随机规模达到1 000次以上时，尺度一致性指标的均值趋于稳定，如图2所示。在其他样本上进行加载也会得到类似的结论。因此，本文设定构造出的原始数据矩阵及随机偏差扰动的次数为3 000次，确保仿真计算出的尺度一致性指标具有足够的代表性和数据稳定性。

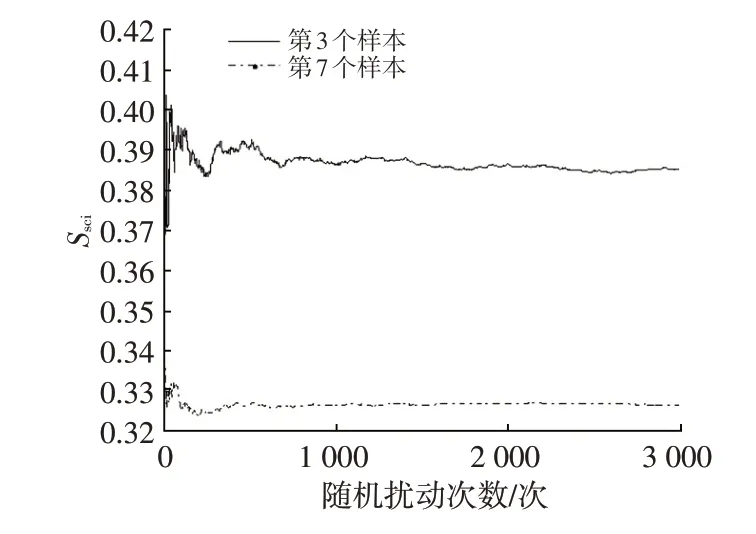
图2 尺度一致性指标统计均值的稳定性

3.2 样本扰动

将不同的随机偏差扰动量加载到单一或多个样本上，模拟评价过程中对某个或某些样本的先入为主的个人偏好。

仿真计算结果表明：随机扰动对加载到任意单个样本上的扰动效果相当，且随着扰动量级的提高明显增加，如图3a所示；扰动效果也会随加载到的样本数量明显提高，但扰动量级的影响相对减弱，如图3b所示。

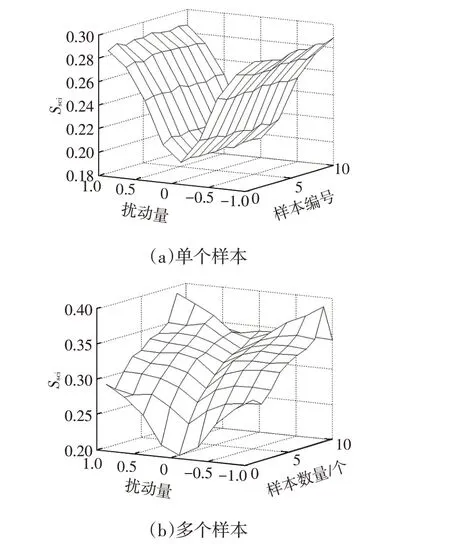
图3 扰动加载样本位置对尺度一致性指标的影响

3.3 样本规模和评价项目规模

为了验证一致性指标应用规模的普适性，根据大多数车辆动力学主观评价活动的样本数量和评价项目数量，将样本规模设定为5～10个，评价项目规模设定为6～12个。

仿真计算结果表明：尺度一致性指标随着变量规模的扩大而增加，同时在任何变量规模下，尺度一致性指标随着扰动量级的提高而明显增加，如图4a所示；在任何样本规模下，尺度一致性指标随着扰动量级的提高而增加，但也会随着样本规模的扩大而明显减小，如图4b所示。

3.4 评价项目

对于评价者在不同评价项目上评价尺度发生变化的情况，由于因子分析前一般会进行数据的标准化，固定扰动值在进行标准化计算后会被去除，因此前文提到的用不同扰动范围叠加随机量的方式不再适用，改为仅用不同量级的随机偏差进行扰动。

在相同扰动量级下，随机扰动加载到任何一个评价项目上基本不影响尺度一致性指标的分布，如图5a 所示，加载到多个评价项目上时，尺度一致性指标会随之明显增加，如图5b所示。

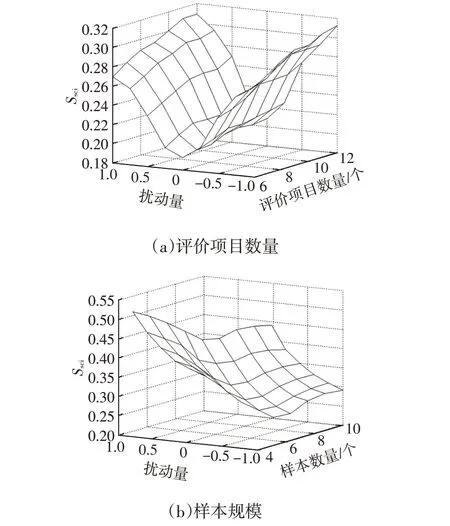
图4 评价项目规模和样本规模对尺度一致性指标的影响

图5 扰动加载评价项目位置对尺度一致性指标的影响

大量的仿真研究表明，只要具有相同的数据结构（即两因子控制），尺度一致性指标均会呈现出与上述仿真类似的规律。

4 结束语

本文通过对主观评价数据的交叉分组及因子分析，构造出可以反映主观评价尺度一致性程度的量化指标。通过在单个或多个样本上、不同样本规模和评价项目规模、单项或多项评价项目上加载随机扰动等仿真分析，验证了尺度一致性指标的普适性和灵敏性。尺度一致性指标是关于主观评价尺度一致性的理想衡量指标，可用于车辆动力学主观评价过程中的评价数据质量判别，也可用于评价者精准分析评价过程中数据的量化偏差。