基于鲁棒优化的随机时变网络最优路径研究
孙世超
(大连海事大学 物流研究院,辽宁 大连 116026)
0 引言
由于道路交通流量的全天变化(早高峰、晚高峰以及午间平峰等),导致城市道路交通网络的路径行程时间(Travel time)具有随时间变化的特征。此外,交通事故、恶劣天气以及偶发的交通拥堵等因素还会导致路径行程时间的不确定性。因此,上述两者共同构成了现实生活中道路交通网络中行程时间的随机时变属性(Stochastic and Time-dependent,STD)。路径行程时间的不确定性和时变特征信息对于出行者来说具有一定的不对称性,这直接影响了出行计划的制定以及最优路径的选择,并会导致出行时间和成本的增加、资源的浪费以及生活质量的降低[1]。
因此,本次研究将综合考虑道路交通网络中行程时间的随机时变特性,并以此作为路网环境的假设条件,对出行路径选择问题进行研究。为了捕获真实交通网络中的这一特性,本文假设先进旅客信息系统(Advanced Traveler Information System, ATIS)能够提供先验的历史交通状态信息,如各个时段所对应的路段行程时间特征等,并在此基础上构建了随机时变网络并模拟建立了行程时间的动态随机变量。随后,针对随机时变网络下最优路径问题,定义了路径选择过程中所考虑的成本费用。由于受行程时间随机时变特征的影响,该候选路径的成本费用同样具有一定的不确定性。因此,考虑通过鲁棒优化的方法,将成本费用鲁棒性最强的路径视为最优路径。最终,通过优化模型的建立、简化与算法求解给出具体的数学分析过程,该研究成果有助于出行线路选取以及交通分配等方面的进一步研究。
1 文献回顾
在随机时变网络中,旅客做出路径选择决策所依据的信息可以被归纳为先验(Priori)信息和在线(Online)信息两类。先验信息是关于道路行程时间日常性波动的总结性描述,例如某一条路径在过去一周的平均行程时间为12分钟。在线信息是关于特定时刻的交通现状描述,例如某条道路上刚刚发生一场事故,可能会导致该条道路瘫痪10到20分钟。本次研究假设先进旅客信息系统(Advanced Traveler Information System, ATIS)能够提供先验的历史交通状态信息用于构建行程时间的动态随机函数,并以此作为随机时变网络中最优路径问题建模的前提基础。
Hall[2]首先提出了利用先验信息解决随机时变网络最优路径问题,并指出在行程时间不确定环境下,基于期望时间成本最小的最优路径选择结果并不是简单一条路径,而是体现了个体的一种策略。随后,一些学者使用随机过程理论来解决上述问题。Psaraftis和Tsitsiklis将路段上的行程时间分布假设为可以根据马尔可夫过程随时间演化,并以此构建优化模型[3]。Azaron和Kianfar将[3]的研究扩展到了解决实际问题中,他们将环境变量演变过程的假设由按照马尔可夫过程演变转至按照独立的半马尔可夫过程演变,收获了很好的效果。然而,上述方法会在一定几率下违背时间窗约束的原则,因此不适用于对于时间可靠性有要求的出行需求[4]。
20世纪90年代以后,一些研究引入了经济学中的效用理论来解决随机时变网络的最优路径问题。对于非平稳(Non-Stationary)的随机网络,Wellman等人在静态网络先入先出(FIFO)原则的基础上,提出了随机一致性原则(Stochastic Consistent Condition),证明了随机优势的广义动态规划方法,并在此条件成立的基础上,提出了改进的基于效用函数的路径规划算法[5]。随后,Wellman又在随机一致性原则的基础上,设计了精确的标签校正算法求解负效用函数问题,寻找期望损失最小的最优路径,但算法的计算复杂度较高,随着网络规模的增加呈指数性增长。
近些年来,通过考虑影响路径选择的因素在“最糟糕情况”下的可靠程度,鲁棒优化理论已经被广泛用于处理路径行程时间不确定性。Bertsimas和Sim提出了一种基于多面体不确定性集的线性鲁棒优化方法[6]。在此基础上,Sim[7]又提出了一种新的鲁棒优化方法,它在理论和实践上都比传统的鲁棒框架有更高的计算易处理性。随后,他证明了随机网络中的鲁棒最优路径问题可以转化为解决一个确定性最短路径问题,从而使计算复杂度大大降低,然而其研究成果并没有进一步将鲁棒优化方法应用于解决随机时变网络下的最优路径问题。
综上所述,以往大量的解决随机时变网络最优路径问题的方法都依赖于获取网络中行程时间变化的概率分布。然而,这一假设条件在实际大规模网络中很难实现,并且会在一定几率下违背时间窗约束的原则,计算复杂度也随网络规模呈几何倍数增长,因此不利于实际大规模网络的应用。本研究将在Sim[7]的研究成果基础上,将鲁棒优化方法引入到解决随机时变网络下最优路径问题中,尝试进行数学模型的简化和问题转化,并寻求适用于大规模城市道路网络应用的低计算复杂度算法且不依赖于先验行程时间概率分布的获取。
2 问题描述及模型建立
2.1 随机时变网络的描述
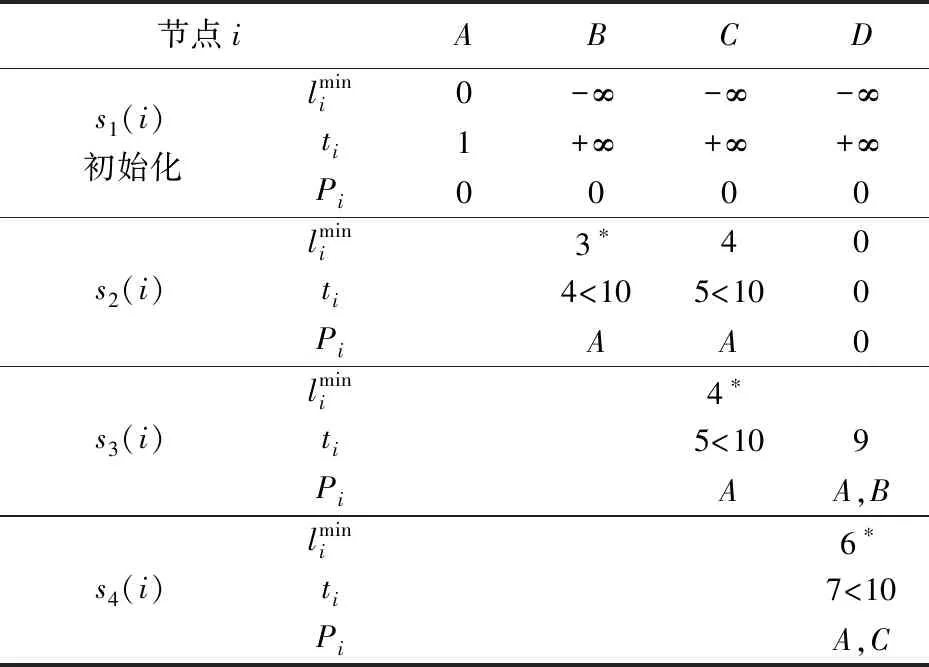
此外,假设上述随机时变网络满足Wellman等人[5]提出的随机一致条件。具体表现为:对于任一路段(i,j),给定任意时间段t (1) 上述不等式是“确定一致性条件”(FIFO性质)的扩充。它代表着对于网络中的同一路径来说,在任何给定时间z之前到达的概率不会因为出发时间的推迟而增加。这个假设与现实世界中的交通网络相一致,即城市道路中确实存在超车现象,但是一般情况下,先出发的车辆在给定时间z之前到达目的地的概率不小于后出发的车辆。 交通网络中最优路径选择标准的定义是本次研究中模型目标函数建立与求解的前提。传统的定义方法是考虑连接起点和终点的候选路径所需的时间成本、金钱成本等要素,通过构建广义的费用函数或负效用函数,以最小化费用成本或负效用值进行最优路径的选取。然而,据上海市第五次综合交通调查显示,该市每日的出行总量中约有58%是出于通勤目的,参加会议或搭乘飞机的商务出行比例也在快速上升。当面临不确定性时,这些到达时间要求严格并带有一定惩罚性质(误机、上班迟到等)的出行更加关注的是行程时间的可靠性以及是否违背时间窗约束。例如,具有不确定性的行程时间会导致旅客抵达目的地的时间与计划到达时间出现晚点或早到的情况,过早的到达目的地会引起等待焦虑并浪费时间成本,而晚点到达的代价更为严重,会造成旅客误机、上班迟到等一系列不便。因此,交通网络中最优路径问题的目标函数定义中逐渐加入了可靠性方面的度量,例如衡量出行时间与计划时间之间的差异——计划时间早到/延迟(Schedule Delays)[8,9]。 然而,随机时变网络中行程时间的不确定性会导致无论选择哪一条候选路径前往目的地,出行者到达终点的实际到达时间不是固定值(某一范围内的随机取值),这同样也会导致此次出行的“计划时间早到/延迟”的不确定性(计划时间早到/延迟=实际到达终点的时间与计划到达终点时间的差值)。对于通勤者来说,迟到会造成不必要的麻烦,而过早到达工作地点意味着浪费了时间的机会成本。因此,本次研究假设迟到不被允许,实际到达时间一定要满足等于或早于计划到达时间。并且,等待时间成本连同出行者在出行过程中花费的在途时间成本,通过在目标函数中被赋予不同的成本惩罚系数,共同构成了本文中所考虑的成本费用(受行程时间的随机时变特征影响,等待时间和在途时间均具有不确定性,因此两者所构成的成本费用也是在某一范围内波动的)。为了实现所做出的路径选择决策具有较强的成本费用可靠性,即不会因为该路径行程时间的不确定因素的极端变化而变差,本次研究将考虑每一条候选路径上述成本费用的鲁棒性,利用鲁棒优化(Robust Optimization)的方法,将成本费用鲁棒性最强的路径视为随机时变网络中的最优路径。 设X是问题的一组可行解。路径λ(λ∈X)表示起始节点O和目的地节点D之间的任意候选路径。Cost(o,λ,t)被定义为在时间段t出发,选择路径λ(λ∈X)连接起始节点O和目的地节点D所需的行程时间。由于行程时间具有不确定性,因此定义MinCost(o,λ,t)≤Cost(o,λ,t)≤MaxCost(o,λ,t)。计划时间早到的成本系数为C,在途时间成本系数为F。本次研究认为等待时间成本小于在途时间成本,因此C 目标函数: F·Cost(o,λ,t1)] (2) 上述模型的目标函数可以改写为: (3) 等同于下式,其中E=C-F<0: (4) 根据3.1节中的变量定义,基于Min-Max准则的随机时变网络中最优路径模型如下: (5) 命题在随机一致性条件下,上述随机时变网络中求解最优路径问题可以简化为求解一个时变网络中的最短路径问题。 证明如式(1)所示,本研究中的网络满足随机一致性条件,因此对于网络中任一路段(i,j)在任何时间段t 可以改写为: (6) 图1 路径λ的图形表示 (7) (8) 步骤2a根据式(1)以及mint2≤t2≤maxt2,可以有如下不等式成立: (9) (10) 不等式右侧的概率是100%,所以得到: (11) 因此,可以确定如果方程(11)总是成立,必须有以下关系成立: (12) 展开后可以得到: (13) 步骤2b同样的,由于t2≥mint2,也有如下不等式成立: (14) (15) 不等式左侧的概率是0,所以可以得到: (16) 若式(16)总是成立,必须有以下关系: (17) 展开后得到: (18) 以此类推步骤3、步骤4等等,直到步骤k-1,旅客到达目的地节点。 步骤k-1假设旅客在时间段tk到达目的地节点nk,可以有以下两个递归公式成立: 递归公式1: (19) 递归公式2: (20) 上述递归公式等价于下列不等式: (21) (22) 对于任何出发时间段t1,上述不等式总是成立的,可以得到: TravelTime=tk-t1 (23) (24) maxCost(o,λ,t1) =max(tk-t1) (25) 因此,Min-Max优化模型(式4)可以被重写如下: (26) 针对解决动态网络下最短路径问题,许多学者已经给出了能够在多项式时间复杂度(polynomial-time complexity)下求解的算法,这也是解决大规模网络问题的前提。本次研究将Sun等人[10]提出的改进Dijkstra算法应用到解决基于鲁棒优化的随机时变网络中最优路径问题,并基于图2中的小型交通网络进行标号法的算例测试。其中,vo代表出发的起始节点,t1代表从vo出发的时间;vd代表需要到达的终止节点,t*代表vd的期望到达时间,即时间窗约束。 图2 随机时变网络测试算例 图3 转换后的确定性时变网络算例 使用Sun等人[10]提出的改进Dijkstra算法,求解图3所示的确定性时变网络中从起始节点vo到终止节点vd的最短路径。其中,算法所涉及的符号定义如下: Pi—节点i当前所有前置节点的集合。 表1 标号法计算过程 由上表,沿着反方向追溯集合Pi中最终存在的前置节点,即可以得到转换后确定性时变网络中的用时最短路径为A-C-D。由于问题的等价性,即随机时变网络中的最优路径同样为A-C-D。为了证明算法的有效性以及求解结果的正确性,应用枚举法获取图2所示的随机时变网络算例中各候选路径到达终点的时间以及成本费用结果,如表2所示。 表2 各路径成本费用结果的变化区间 从表2中可以看出,在迟到被禁止的情况下,路径A-C-D确实具有更强的成本费用鲁棒性。并且,基于Min-Max准则下,所提出的优化模型与采用的改进Dijkstra算法切实有效。 在随机时变网络条件下,针对出行者对行程时间可靠性以及时间窗约束的不断关注,本文定义了该网络环境下路径选择过程中所考虑的成本费用,并通过鲁棒优化的方法,将成本费用鲁棒性最强的路径视为最优路径。随后,建立了基于Min-Max准则的随机时变网络最优路径模型,并在随机一致性条件下,通过数学推导证明了该模型可以简化为解决一个确定性时变网络中的最短路径问题。具有多项式时间计算复杂度的改进Dijkstra算法被应用到模型的求解中,并通过小型算例证实了模型及算法的有效性。 未来研究将更多的关注大规模实际交通网络的计算测试以检验所提出方法的适用性和算法效率。由此还需进一步证明随机一致性条件的适用性范围以及研究路段行程时间波动的规律性数学描述问题。2.2 最优路径定义方法
2.3 基于Min-Max准则的随机时变网络最优路径模型
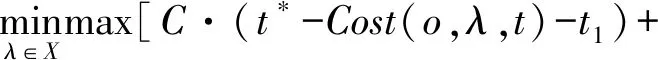
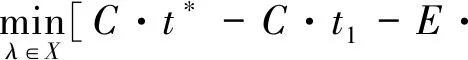
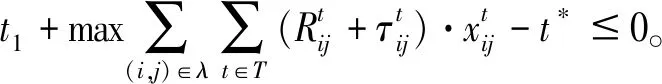
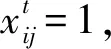
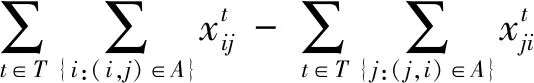
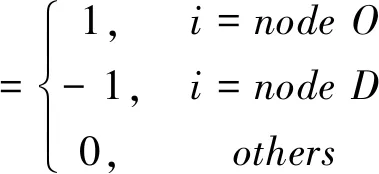
3 模型简化的数学推导过程

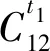
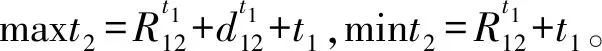
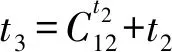
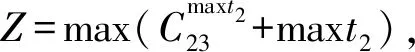
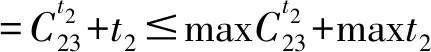
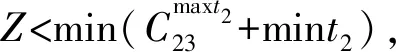
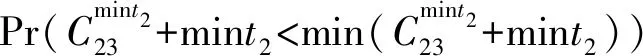
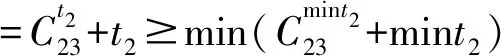
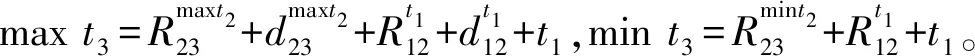
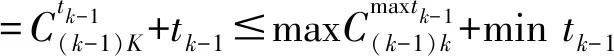
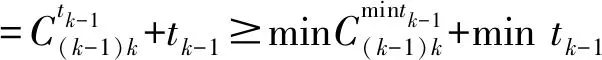
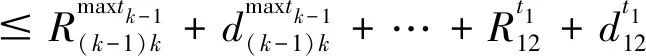

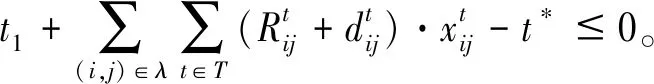
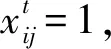
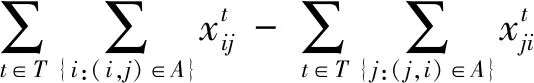
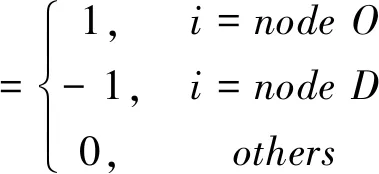
4 算例测试
4.1 测试算例
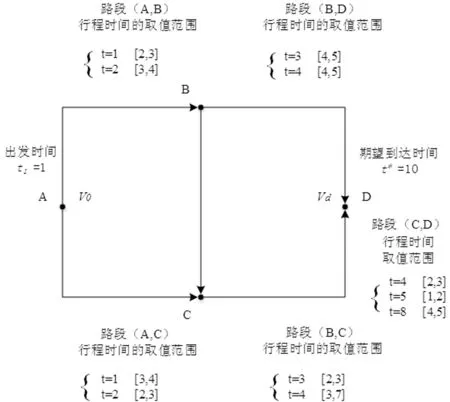
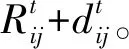
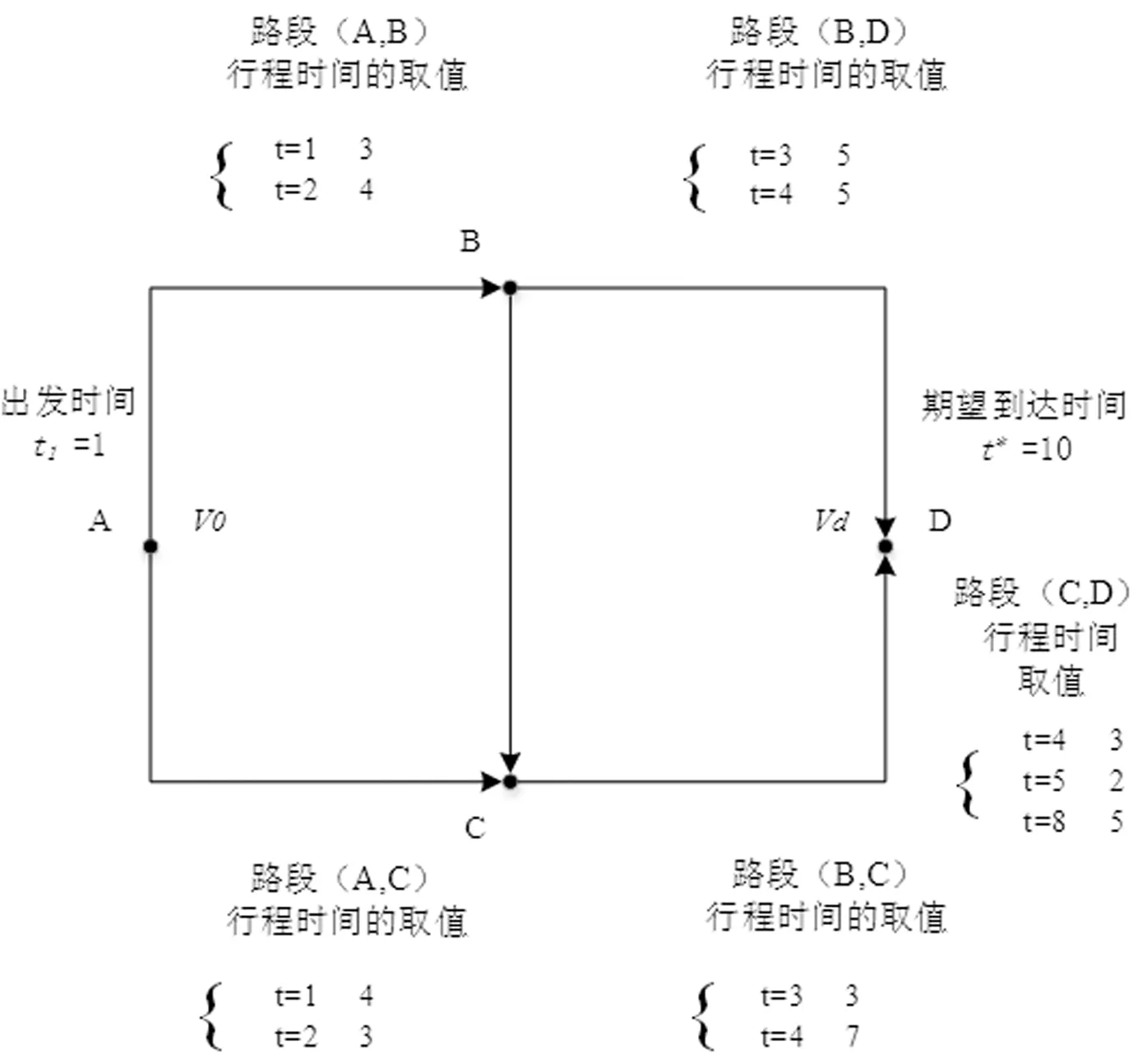
4.2 标号法的计算过程与结果分析
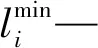
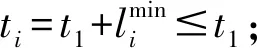

5 结论

