随机服务时间下异质患者门诊预约调度优化

张文思, 李金林, 冉 伦, 王 伟

(1.中国海洋大学 经济学院，山东 青岛 266100; 2.中国海洋大学 海洋发展研究院，山东 青岛 266100; 3.北京理工大学 管理与经济学院，北京 100081)

0 引言

门诊是患者在就诊过程中最早、也是最频繁接触的场所，其服务效率和服务质量会直接影响后续部门、甚至整个医院的工作效率，因此门诊资源的调度与优化一直是医疗服务运作管理研究的重点和热点[1]。在新医改的不断推进下，门诊预约挂号服务得到高度重视和推广。以北京市为例，自统一预约挂号平台开通以来，市属医院整体预约挂号率已从2012年的52.2%提高到2018年的88%。

实际操作中，由于患者服务时间的随机性，会导致预先为患者分配的服务时间与患者实际接受服务时间的不一致。若为患者设定较早的服务开始时间，可在一定程度上提高医疗资源的使用效率，但会发生新患者到达时前序患者仍未结束服务的情况，增加患者等待时间，使患者满意度降低；设定较晚的预约时间可减少患者等待时间，但若当前患者结束服务时后序患者仍未到达，就会造成医疗资源的闲置与浪费。因此在随机服务时间的假设下，如何权衡患者等待时间和医生空闲以及加班工作时间，设计合理的预约调度机制，实现医疗服务系统成本的最小化，是医疗服务提供者需要考虑的关键问题之一。

自Bailey[2]和Lindley[3]的开创性工作以来，门诊预约调度问题受到了越来越多的关注[4～7]。Wang[8]在患者服务时间为独立同分布的指数变量时，指出最优预约时间间隔服从先增加并维持在一个较高水平然后逐渐递减的“dome”形模式，Robinson和Chen[9]将这一结果扩展到了服务时间服从一般分布的情形，Denton和Gupta[10]基于两阶段动态线性规划模型求解门诊预约中患者的最优时间间隔，并证明了dome型预约规则会大幅提高门诊服务效率；Kupier和Mandjes[11]将该研究扩展至两阶段串行排队的治疗过程。

在现实的门诊预约问题中，提前预约的患者可能因为各种原因在就诊当天没有前往医院接受服务，即发生患者爽约(no-show)[12]；此外，不同患者的爽约率、治疗时间也不同，即患者为异质的(heterogeneous)[13]。Ho和Lau[14]研究了患者爽约率、服务时间变动系数和单位服务时间患者数量三个变量对预约调度规则的影响；Liu等[15]基于经典排队论模型，考虑患者爽约率与预约-服务时间间隔的相关关系，设计了相应的超订机制。同时考虑患者异质性和爽约行为的研究相对较少，其中Zacharias和Pinedo[16]研究了患者爽约率和等待时间成本不同的异质患者的预约调度准则，Lee等[17]基于两类患者期望服务时间和爽约率的不同，设计了固定到达时间间隔的门诊预约调度问题。

给定一组患者，决策者对患者预约时间的决策等价于：(1)决定患者的服务顺序，即患者排程，(2)给定患者排序的前提下，决定分配给各个患者的服务时长，即患者调度。基于此，本文将在上述研究内容的基础上，在患者服务时间随机的假设下，考虑患者服务时间分布和爽约行为的不同，对异质患者的预约方案进行优化，以最小化患者等待时间、医生空闲和加班时间成本，提高医疗资源使用率。

本文其余部分组织如下：第1部分对随机服务时间的预约调度问题进行描述并给出相应的符号说明和模型假设；第2部分首先建立不考虑患者排序的预约调度模型，求解患者调度方案，并在此基础上设计启发式排序准则，同时优化患者的服务顺序和服务时间；第3部分通过数值算例对启发式预约调度方案的效率进行说明，并与样本平均近似方法获得的结果进行对比分析，最后给出结论和管理启示。

1 问题描述与符号规定

考虑单服务台的预约调度系统，患者为服务时间分布各不相同且相互独立的异质患者；已预约患者在就诊当天可能会发生爽约行为。假设医生正常服务时间和患者数量固定，正常工作时间内未能接受服务的患者需医生加班完成服务。本文将以最小化患者等待时间成本、医生空闲与加班成本为目标，决策各个患者的服务开始时间。

本文所用到的符号说明如下：

(1)参数

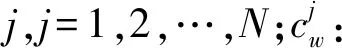
(2)决策变量

a=(aij)N×N:分配矩阵，aij=1表示将患者i指派至第j个位置，否则aij=0；

s=(s1,s2,…,sN):决策向量，其中sj表示分配处于位置j的患者的服务时间；

dj(a,x):给定分配矩阵a后处于位置j的患者随机服务时间；

bj(a):给定a，bj(a)=1表示处于位置j的患者在就诊当天出现，否则bj(a)=0；

wj(a,s,x):给定分配矩阵a后处于位置j的患者的等待时间；

lj(a,s,x):给定分配矩阵a后处于位置j和位置j+1的患者之间的医生空闲时间；

o(a,s,x):医生加班时间。

根据本文研究问题的特点，现做如下模型假设：

(1)患者服务数量固定，患者服务时间分布信息和行为特征信息可根据历史数据获得；

(2)不同患者的随机服务时间以及就诊当天发生爽约的行为相互独立；

(3)患者随机服务时间为单峰(unimodal)分布；

(4)患者准时到达系统，不考虑患者迟到、提前到达的情况。

若令第一个患者在0时刻到达，根据上述符号参数及模型假设，第二个患者的预计服务开始时间为s1，第三个患者预计服务开始时间为s1+s2,…,依此类推。

2 模型分析与求解

引入一个服务时间为零且在就诊当天出现概率为1的虚拟患者N+1，该患者在医生正常工作时间结束时(时刻T)到达，则其等待时间即为医生加班时间。根据模型假设，上述问题可采用如下随机混合整数规划模型进行描述:

(1)

s.t.wj+1(a,s,x)=(wj(a,s,x)+

bj(a)dj(a,x)-sj)+,j=1,2,…,N

(2)

lj(a,s,x)=(sj-wj(a,s,x)-bj(a)dj(a,x))+,

j=1,2,…,N

(3)

(4)

(5)

(6)

w1=0

(7)

(8)

(9)

aij∈{0,1}

(10)

s≥0

(11)

约束条件(2)和(3)分别定义了患者等待时间和医生空闲时间，并保证了若患者在就诊当天爽约，则不产生患者等待时间成本，且该患者服务时间为零。约束条件(4)和(5)说明当且仅当患者i在第j个服务时，才会在该位置产生服务时间和等待时间成本。约束条件(6)表示所有患者分配时间总和为医生正常服务时间T，即将医生正常服务时间分配给N个患者，约束条件限制了第一个患者在t=0时到达。(8)～(10)保证了每个位置必须且仅能安排一个患者，每个患者只能被安排一次。注意到医生加班时间等于虚拟患者N+1的等待时间，即o(a,s,x)=wN+1(a,s,x)，则原问题可改写为：

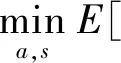
(12)

满足约束条件(2)～(11)。

根据式(12)，若第j个患者在就诊当天爽约，则相当于该患者的服务时间和等待时间均为零；若该患者在就诊当天出现，则服务时间为满足已知分布函数的随机变量，等待时间取决于其前序患者的等待时间和服务时间。由符号假设可知当给定指派矩阵a时，第j个患者在就诊当天到达系统的概率为

(13)

根据Begen和Queyranne[18]，可利用患者出现的概率αi计算第j个患者的期望服务时间xj，以此代替患者服务时间；由于调整后的服务时间已经考虑了患者的行为特征，简便起见，在随后的分析中可忽略患者爽约行为，将模型简化为：

(14)

s.t.wj+1(a,s,x)=(wj(a,s,x)+

dj(a,x)-sj)+,j=1,2,…,N

(15)

lj(a,s,x)=(sj-wj(a,s,x)-dj(a,x))+,

j=1,2,…,N

(16)

约束条件(4)～(11)。

2.1 不考虑患者排序的调度方案

在预约调度优化中，可将问题分为调度和患者排程两阶段进行求解。对于目标函数(14)，将其等价为

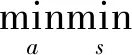
(17)

给定患者排程方案a，则原问题转化为寻找最优分配方案s，使系统总成本最小。

若系统中只有两名患者且患者到达顺序固定，令第一个患者的到达时间t=0，则此时唯一的决策变量为第二个患者的到达时间，即分配给第一个患者的服务时间s1。不考虑医生加班成本，可将上述患者预约调度优化与随机需求下的库存问题等价(Weiss)[19]，当存在医生加班成本时，根据前述符号假设，目标函数可写为：

(18)

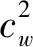
d1(s,x)=(s1-x1)+,w2(s,x)=(x1-s1)+

d2(s,x)=(s2-x2-w2)+

w3(s,x)=o(s,x)=(x1+x2+d1-T)+

(19)

求解式(18)关于s1的一阶条件，有：

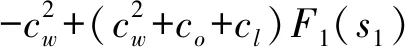
-(co+cl)F1(s1)F2(T-s1)=0

(20)

(20)式提供了当系统中存在两个患者时分配给第一个患者最优服务时长的隐式解，当不考虑医生加班时间成本和医生提前完成服务的空闲时间(即d2)时可得最优解如下[19]：

(21)

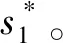
下面考虑如何将两个患者的情形扩展至系统中存在多个患者的情况。注意到，当患者数量N=2时，通过式(21)虽不能获得最优服务时长的闭式解，但可通过数值计算得到分配给第一个患者的最优服务时长。因此可以考虑将患者分为两个部分，并将两部分患者分别看作单一患者进行求解。由此可提出如下算法：

算法1

Step1初始化患者集合P={1,2,…,N}和医生正常服务时间T，j=N；

Step2将患者集合分为两个子集，其中P1={j}，P2=P/P1；

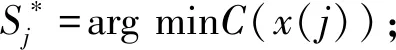
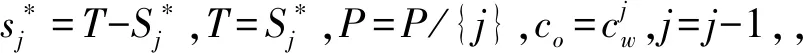
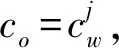
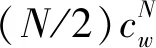
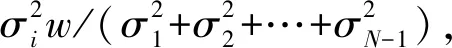
(22)

算法2(修正后的算法1)

Step1初始化患者集合P={1,2,…,N}和医生正常服务时间T，j=N；

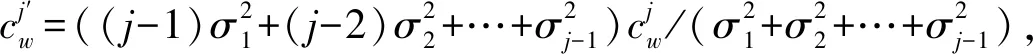
Step3利用算法1，求解患者最优调度方案。

2.2 考虑患者排序的调度方案

2.2.1 样本平均近似

当同时考虑患者服务时间和服务顺序时，由于服务时间的不确定性，直接求解随机混合整数规划模型比较复杂，为降低求解难度，现有研究常采用样本平均近似(sample average approximate approach，SAA)方法对模型进行近似。SAA方法利用患者服务时间的样本值将随机问题转化为确定性问题求解，不需要考虑患者服务时间的分布信息，从而降低了计算的复杂性。为更好地说明并建立SAA模型，需引入如下参数和变量：

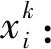
gk:提前时间，即服务完最后一个患者比医生正常工作时间T提前的时间；M1,M2充分大的正数。

其他参数和变量的定义与随机模型相同，基于SAA方法，可将模型(14)改写为：

(23)

(24)

(25)

(26)

(27)

aij∈{0,1}

(28)

(29)

(30)

(31)

(32)

ok≥0,k=1,2,…,K

(33)

约束条件(24)和(25)定义了各样本下的患者等待时间和医生空闲时间，(26)～(28)保证了每个患者都被安排到队列中的某个位置上，且每个位置只安排一名患者。约束条件(29)～(33)表示患者等待时间、医生空闲和加班时间非负，当且仅当患者i被安排至第j个位置服务时，患者i会在j位置产生等待成本或带来医生空闲成本。

上述混合整数线性规划问题可通过优化软件CPLEX求解，Mancilla和Storer[20]证明了当同时考虑患者服务时间和服务顺序时，上述问题为NP-hard问题，并通过数值实验指出当仅考虑10个患者、100个样本时，采用CPLEX求解该类问题最优解的时间长达数十小时甚至几天。而若给定患者排序，该方法可较快获得一个近似最优解，因此在数值算例中将以确定服务顺序的SAA模型求解结果作为基准解进行比较分析。

2.2.2 启发式排序方法

考虑到直接求解随机混合整数规划和SAA方法的计算复杂性，根据算法1和算法2的思想，可设计如下算法求解分配给各患者的服务时间和服务顺序。

算法3

Step1初始化患者集合P={1,2,…,N}，j=N；

Step2对任意i∈P，将患者集合分为两个子集，其中P1={i},P2=P/P1；

Step3将集合P2中的患者看作一个整体，并令服务顺序为P2P1，将原问题转化为两个患者的预约调度问题，利用式(22)修正患者等待时间成本，根据式(20)求得最优解和最优期望利润C*(i)；

与算法2相同，考虑到集合P2内患者之间的等待时间，也需要对患者单位等待时间成本进行调整。但与算法2的不同之处在于，算法2在对患者等待成本进行修正时，所有患者的服务顺序已知，而在算法3中患者服务顺序是不确定的，当患者服务时间方差不同时，根据式(22)，P2中各个患者对P1患者等待时间的影响也会随着服务顺序的改变而不同。因此需要进一步考虑如何确定集合P2内患者的服务顺序。

Denton等[21]在患者的等待时间成本相同的假设下，利用凸序理论给出了考虑医生加班时间下两个患者的最优服务顺序。当患者等待时间成本不同时，有：

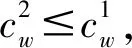
证明当系统中只有两个患者时，由式(20)，根据最优服务时间的一阶条件，假设服务时间为服从独立同分布的随机变量，对第二个患者等待时间成本cw求导，得：

(34)

根据式不难发现∂s1/∂cw>0，即当第二个患者的等待时间成本较高时，决策者往往会给第一个患者分配较长的服务时间以减少第二个患者的等待时间。此外，由式(12)和(19)，可得系统总期望成本为:

C=E[cw(x1-s1)++co(x1+x2+(s1-x1)+-T)++cI(s1-x1)+]

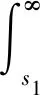
(35)

对式(35)关于cw求导，

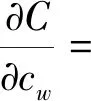
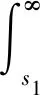
[cw+(cw+cl+co)F1(s1)+

(36)

由式(20)，显然∂C/∂cw>0。

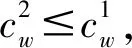
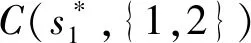
其中第二个不等式由凸序(convex ordering)的定义和期望等待时间、医生空闲时间和加班时间的凸性可得。

当患者数量N≥3时，定理1和定理2的结论不再适用，但仍可为后续设计启发式排序算法提供思路。根据Mak等[22]，给出如下几种常见的启发式排序方法：

(1)方差序(Order of variance，OV)。当患者等待成本相同时，Weiss[19]、Denton等[21]指出可采用方差增序对患者进行排序。由于患者服务时间的方差体现了服务时间的波动性，因此排序时将服务时间方差较小的患者放在前面，可减小方差波动对后序患者的影响。

(2)方差-等待成本比率(Order of variance-to-waiting cost ratio，OVC)。根据定理1，若患者方差相同，则最优服务顺序为按照等待时间成本降序排列，这是因为在整个服务队列中顺序相对较前的患者等待时间往往较短，而位置相对靠后的患者由于前序患者服务时间的波动，往往需要等待较长的时间，因此可以将等待时间成本高的患者安排在队列前面。同时由于服务时间方差会带来服务时间的波动性，由Gupta[23]，可按照服务时间方差与患者等待成本之比σ2/cw的增序进行排列。

(3)标准差-等待成本比率(Order of standard deviation-to-waiting cost ratio，OSC)。与(2)类似，根据Mak等[22]，可利用服务时间标准差与等待成本比率的增序对患者进行排列。

下面给出基于启发式排序方法的求解算法：

算法4

Step1初始化患者集合P={1,2,…,N}；j=N;

Step2对任意i∈P，将患者集合分为两个子集，其中P1={i}，P2=P/P1；

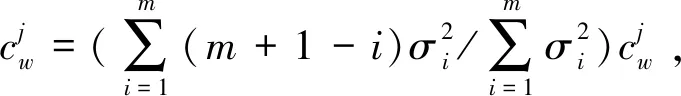
2.3 患者服务时间分布卷积的简化计算

注意到上述算法均需要计算集合P2内患者随机服务时间之和的分布函数，即需要计算各个患者服务时间分布的卷积。首先考虑两个连续随机变量和的分布，若X1，X2是两个相互独立的随机变量，则X=X1+X2的概率分布可由卷积公式得到：

Y=X1+X2+X3的概率分布可通过计算X(=X1+X2)与X3的卷积得到，以此类推。根据卷积计算公式可发现，当随机变量的概率密度函数形式复杂时，卷积的计算难度也会加大。

下面通过将连续分布离散近似以对卷积计算进行简化。对于两个离散序列x1(n)和x2(n)，其卷积x(n)可通过如下表达式给出：

记患者i的服务时间xi概率密度函数为fi(·),i=1,2,…,N,fi(·)为单峰函数。考虑区间[0,Tmax]，其中Tmax表示P2中患者服务时间之和的最大值。将区间[0,Tmax]以为Δt间隔等分为M份，即Δt=Tmax/M，当Δt足够小时，可将离散化的概率密度函数近似作为连续分布的概率密度函数。根据离散序列的卷积公式，有：

……

h1(·)、h2(·)分别为x1+x2、x1+x2+x3的概率密度函数，同理可得到x1+x2+x3+x4，x1+x2+x3+x4+x5等的概率密度函数。

3 数值算例

本节通过数值算例对算法的有效性加以验证。首先假设患者服务时间为独立同分布的随机变量，且患者等待时间成本相等，此时无需考虑患者排序。Denton和Gupta[10]利用L-shape算法求解了基于两阶段随机规划的调度问题，并以较高的精度给出了最优解的上下界，因此可将L-shape算法获得的结果作为最优解，将启发式算法的结果与L-shape算法进行比较，验证算法的有效性。

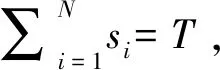
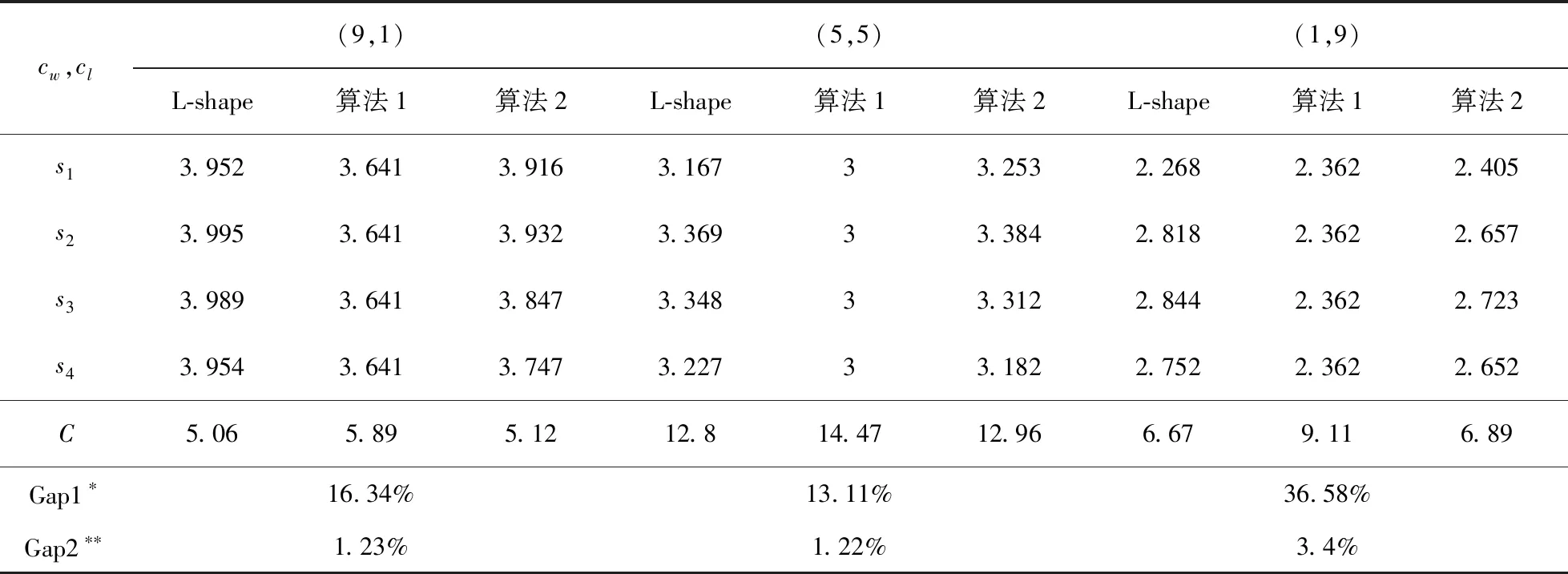
表1 不考虑医生加班时间的调度方案期望成本比较

*Gap1=(C1—CL-shape)/CL-shape，**Gap2=(C2—CL-shape)/CL-shape;C1、C2分别表示利用算法1和算法2求解患者调度方案获得的系统期望成本。

当医生加班成本不为零时，假设患者服务时间服从均匀分布U(0,2)，不同患者的等待时间成本相等。与Denton和Gupta[10]一致，令N=7，表2比较了不同成本参数下算法1、算法2和L-shape算法得到的系统期望成本，图1给出了不同成本参数下三种算法分别为患者分配的服务时间。根据表2可发现，对等待时间成本进行修正的算法2明显改善了算法1，且算法2获得的系统期望成本与L-shape算法结果差距较小，从而验证了算法2的有效性。

表2 不同参数下的期望成本比较

*Gap1=(C1—CL-shape)/CL-shape，**Gap2=(C2—CL-shape)/CL-shape；C1、C2分别表示利用算法1和算法2求解患者调度方案获得的系统期望成本。

图1 不同参数下算法结果比较

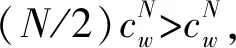
再来看同时考虑患者服务时间与服务顺序的问题。为与SAA方法的患者排序方式保持一致，均采用方差-等待成本比率(OVC)的启发式排序方法给定患者服务顺序，通过算法4获得患者服务时间，并将结果与通过CPLEX软件求解模型(23)得到的结果进行对比。

假设系统中共有7位患者，服务时间分别服从均匀分布U(0,4),U(0.2,3.8),U(0.5,3.5),U(1,3),U(1.2,2.8),U(1.5,2.5),U(1.8,2.2),患者单位时间等待成本向量为cw=[9,8,3,4,5,6,7]，表3对比了当成本系数不同时，样本均值近似方法与算法4在不同样本数量下获得的结果。

根据表3可发现，在不同的参数组合下，当样本规模K≤10000时，基于算法4的预约调度方案得到的系统期望成本低于给定患者服务顺序时利用SAA方法获得的结果，且随着样本数量的增加，SAA方法获得的结果会得到改善并收敛于最优，但所需求解时间较长，算法4在一定程度上保证求解质量的同时减少了计算时间，由此体现了算法4在计算时间和效率上的优越性。

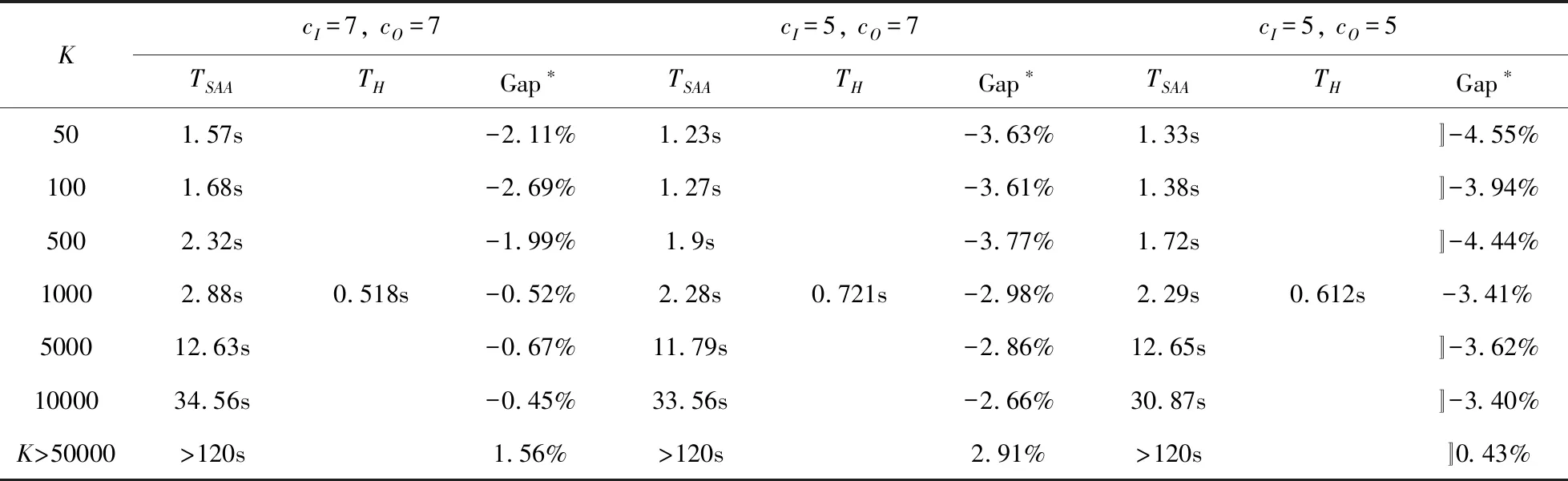
表3 算法4与SAA结果对比

*Gap=(CH—CSAA)/CSAA，TH表示利用启发式算法4求解原问题所需要的计算时间;CH表示利用启发式算法4求解患者调度方案获得的系统期望成本。

图2 算法4与SAA算法获得的患者调度方案对比

图2给出了不同医生空闲成本和加班时间成本下，基于不同样本数的样本均值近似方法获得的患者预约调度方案以及基于算法4获得的患者预约调度方案，从图中可以看出，两种算法下分配给各个患者服务时间变动的趋势一致，且随着样本数量的增加，两种算法下的预约调度方案趋近一致。根据图2还可发现，两种算法给第5个患者分配的服务时间最长，给第6个患者分配的服务时间最短。这是由于按照方差-等待成本比率增序对患者进行排序时，根据患者方差和等待成本参数，排在第5个和6个进行服务的患者分别为患者2和患者1；患者2的等待时间成本最小，且小于医生空闲时间成本，决策者会减少分配给前4个患者的等待时间以减小医生空闲时间，而患者1等待时间成本最高，因此会为前5个患者分配更多的服务时间，以减少患者1的等待时间。

表4进一步对比了不同患者数量下算法4与SAA的计算结果，当样本数量较少时，基于算法4的预约调度方案在计算时间和计算效率上均优于SAA方法，随着患者数量和样本数量的增多，SAA方法所需计算时间显著增加，由此进一步体现了算法4在计算效率上的优势。

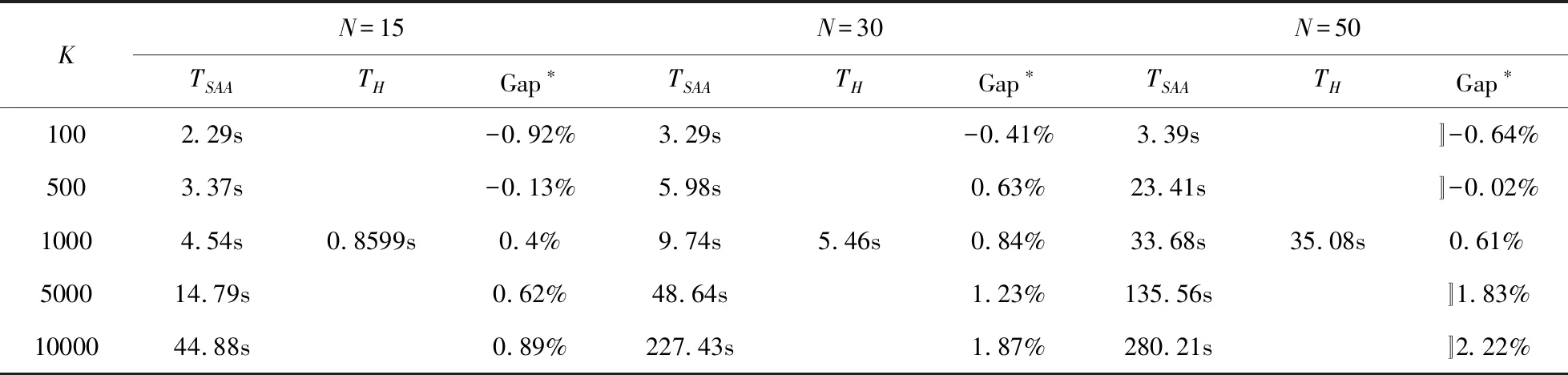
表4 不同患者数量下算法4与SAA结果对比

*Gap=(CH—CSAA)/CSAA，TH表示利用启发式算法4求解原问题所需要的计算时间；CH表示利用启发式算法4求解患者调度方案获得的系统期望成本。

4 结论

本文研究了单服务台的随机预约调度模型，针对服务时间随机的异质患者，考虑患者服务时间分布函数和爽约行为的不同，建立随机混合整数规划，对患者的预约调度方案和服务顺序进行优化。首先给定患者服务顺序，求解了两患者预约系统最优方案满足的一阶条件。进一步的，设计启发式算法对多个患者的预约系统调度方案进行求解，并通过对患者等待时间成本系数进行调整以修正算法。在此基础上，对患者的排序方案进行优化，确定各个患者的服务开始时间。

数值结果表明，当患者服务时间为独立同分布的随机变量时，分配给患者的服务时间呈现先增加并维持在一个较高水平，后逐渐减少的“dome”形，即给较早接受服务的患者和最后接受服务的患者预留较短的服务时间，而给服务顺序处于队列中间的患者预留较长的服务时间；当患者服务时间分布互不相同时，与基于样本均值近似方法的结果相比，启发式算法在求解效率和计算时间上都具有一定的优越性。

当患者等待时间成本较低时，根据数值结果，系统会为队列中间的患者安排较长的预约时间间隔，若当前患者在下一个患者到达前结束服务，则会造成医生空闲时间。由于医疗服务过程中，医生空闲往往伴随着设备空转、医疗资源闲置等，空闲时间成本往往较高，实际应用中，医院可考虑在医生服务能力范围内，安排部分当天到达的患者接受服务，以减少医疗资源的闲置；同时，为提前预约患者赋予较高的优先权，防止预约患者因等待时间过长而造成的满意度下降。在对患者的服务顺序进行决策时，需要权衡患者等待时间成本和随机服务波动性对系统的影响，将服务时间波动较小、等待时间成本较高的患者指派至等待队列的前面接受服务，将服务时间波动性大且等待时间成本较小的患者安排在后面接受服务，以最小化由于患者服务时间的波动性对系统造成的影响，并减少预约调度系统总成本。