多目标应急物流中心选址的鲁棒优化模型

赖志柱， 王 铮,2， 戈冬梅， 陈玉龙

(1.华东师范大学 地理信息科学教育部重点实验室,上海 200241; 2.中国科学院 科技战略咨询研究院,北京 100190; 3.贵州工程应用技术学院 生态工程学院，贵州 毕节 551700)

0 引言

现实生活中频繁出现各种天灾、人祸等重大突发事件，这严重影响了正常的社会秩序，造成巨大的人员伤亡和经济损失，因此针对灾害应急和灾害应急系统工程的研究和管理工作具有重要的价值和意义。当突发事件，尤其是重大灾害事件发生后，要快速启动应急救援系统，向受到灾害侵袭的地区和人员运送充足的各种物资应付危机。由于各种突发事件的发生很难提前预测，以及灾害发生的损害程度也无法准确估计，一旦发生严重突发事件，尤其是自然灾害(如地震、台风或海啸)，通常波及范围较大，影响时间较长，给应急救援带来巨大挑战。为了将救援物资尽快运送到受灾地点，预先将救援物资存放在一个接近灾难可能发生位置的应急救援设施中，是目前缩短救援物资送达时间和控制救援成本、提高救援效率的常用有效的应急策略。应急救援物资的高效调配运输对灾后援救工作的有效开展具有极其重要的作用，因而对应急救援物资的收集、运输和配送就构成了应急物流系统的核心内容。应急救灾网络规划是应急救援和应急响应中非常重要的一环，合理的规划可以大幅度提高应急物资的调配效率和效果，通常涉及两类问题的研究：应急设施选址和应急物资配置问题。

应急设施的研究最早可追溯到Hakimi[1]提出的P重心和P中心问题、Roth[2]和Toregas et al.[3]分别提出的集合覆盖问题以及Church和ReVelle[4]提出的最大覆盖问题，后续的应急设施选址模型大多是在这三种模型基础上改进或变化而来。Overstreet et al.[5]在梳理大量应急物流文献后，阐述了应急物流规划的复杂性及下一步的研究方向；Galindo和Batta[6]梳理了2005～2012年的大量应急物流建模方面的文献，发现应急物流规划使用最广泛的方法仍然是数学规划，并着重讨论了模型假设部分的实用性；Caunhye et al.[7]指出多目标方法和动态规划是应急物流的进一步热点研究方向。

在应急设施选址及应急物流方面，Ozdamar et al.[8]探讨了自然灾害发生后的应急物流和应急物资配置问题，随后Yi和Ozdamar[9]以物资送达及救治伤员的延误最小化为目标而建立了一种确定性应急物流选址模型；Horner et al.[10]结合GIS研究了应急救援物资的配送问题；Kar et al.[11]构建了应急避难场所选址的线性组合模型；Widener et al.[12]探讨了应急救灾物资的分层选址模型。我国学者在应急研究方面起步相对较晚，欧忠文等[13]最先明确提出应急物流的概念，阐述了应急物流中各项关联机制，并提出设立应急处理机构和构建应急技术平台；王旭坪等[14]通过分析应急物流及应急物流系统设计的相关特征，提出构建应急物流系统的结构和快速反应机制；曾敏刚等[15]以台风灾害为背景，研究了应急物流减灾系统的选址-路径问题；王铮等[16]研究了层次型应急设施布局模型并成功应用于上海市某区的医疗设施布局；葛春景等[17]引入最小最大临界距离和覆盖水平函数，构建了多数量多质量覆盖模型并改进遗传算法求解；郑斌等[18]研究了震后初期应急物流系统的选址-多物资配送问题，构建了一个考虑配送时间和物资分配公平性的双层规划模型。上述这些研究分别在应急物流选址的概念、特征、系统、模型设计、求解算法方面做了有益的探索，但这些研究都没有考虑问题本身及数据获取的不确定性，且均以单目标模型为手段讨论并解决问题。在多目标模型方面，陈志宗等[19]基于应急救援设施的公平性和效率性，整合了多个传统的设施选址模型并通过实例验证模型的正确性；丁雪枫等[20]构建了一个考虑总成本、公平性和效率性的多目标应急设施选址问题；朱建明[21]从时效、均衡和鲁棒等三个角度构建多目标应急设施选址优化模型；冯舰锐和盖文妹[22]根据应急物资调度的时效性和经济性特征，构建了应急选址多目标优化模型。这些文献将应急问题定位为确定性问题，而没有考虑应急问题包含的各种不确定性。

在处理问题的不确定性方面，通常使用两种方法，随机优化和鲁棒优化。随机优化是一种比较常用的经典方法，其目标通常是最小化所有情景下的期望成本或最大化所有情景下的期望收益。如Schilling[23]在研究最大覆盖选址问题时引入了情景的概念，其目标为最大化所有情景下覆盖的需求数；Jornsten et al.[24]建立了一种基于情景的最小化期望成本的设施选址模型，其目标为最小化所有情景和所有时期内的期望成本。此外，也有学者利用模糊数[25,26]、区间数[27]或区间灰数[28]等描述及解决应急物流问题的不确定性。另一种方法，鲁棒优化来源于鲁棒控制理论，可视为随机优化和灵敏度分析的补充替换，其特点是不需要知道不确定参数的概率分布。最小化最大成本(minimax cost)或遗憾(minimax regret)形式的鲁棒模型最早由Serra et al.[29]和Averbakh et al.[30]分别独立提出，这种minimax形式的鲁棒优化引起了众多研究者的兴趣。如姜涛等[31]利用鲁棒优化方法研究了有限期要求单目标应急设施选址模型；王晶等[32]构建了应急物流配送中心选址的相对鲁棒模型；冯春等[33]构建了应急物资储备库选址问题的单目标鲁棒优化模型和随机优化模型；刘慧和杨超[34]构建了服务设施选址问题差异形式的鲁棒优化模型；彭春等[35]引入box和ellipsoid不确定集合描述应急资源成本的不确定性，构建了多类应急资源选址-路径鲁棒优化模型。上述研究都是在单目标背景下利用鲁棒优化方法研究应急设施选址问题，且大多数为简化模型仅考虑单一的应急物资。

进一步，众多学者将多目标模型(或隐含多目标思想的多层多阶段角度)和鲁棒优化方法相结合。孙华丽等[36]利用对称区间表示不确定性，构建了多物资多运输车辆多阶段应急物流选址-路径的相对鲁棒优化模型；钟慧玲等[37]将p-鲁棒概念引入危险品道路运输应急设施选址问题中，构建了目标分层的p-鲁棒弧段覆盖模型；张铱莹[38]将应急需求点的危险权重概念引入应急设施选址模型；何珊珊等[39]研究了不确定需求下应急物流系统多目标优化模型；张玲等[40]利用区间型不确定集合描述需求量，构建了应急救灾网络的两阶段混合整数规划模型，并转化为可调整鲁棒对应问题求解；杜博和周泓[41]针对协同优化“预选址-重选址”而构建了两阶段应急设施选址鲁棒优化模型。上述研究通常是将多目标其转化为单目标或利用目标规划处理，但简单的线性加权法又忽略了目标之间的单位差异；利用百分比无量纲化后再利用目标规划求解的方法，又无法真正消除目标值之间可能存在的巨大的数量级差异。

综上所述，既有研究在应急设施选址方面已经取得了丰硕的成果，但对于应急物流选址及应急物资调运的信息不确定性以及对不确定性的处理方面尚有不足。多数文献研究的是单一应急物资情况，极少数文献研究了多类应急物资情况；多目标应急物流选址方面，多数文献采用多目标转化为单目标的思想和方法，但这些方法并不能很好地处理多个目标之间的单位差异及其数量级差异；多数文献研究不确定性时，均考虑的是问题参数的不确定性，而没有考虑应急救援过程可能会依据不同救援阶段而导致决策的不确定性。实际上，对于应急救援问题，应急救援成本和应急救援时间两个目标可能不是同等考虑的，可能与应急救援阶段有关或与决策者的决策有关。为此，我们引入情景来描述应急物流设施(物资收集点和应急物流中心)的各种不确定性，建立多目标应急物流中心选址的确定型模型和鲁棒优化模型，并引入成本偏好权重来描述各个救援阶段的划分或决策者的不同决策要求，通过单目标情况下的最优解除多目标问题对应目标值为无量纲化数值，从而将多目标问题转化为单目标问题，最后设计了通用的混合蛙跳算法来优化求解。

1 数学模型

1.1 问题描述

我们考虑重大突发事件(如地震、台风等自然灾害)发生后，需要在灾区或邻近地区迅速组建若干应急物资收集点和应急物流中心，在有限的时间、空间和资源约束下，同时考虑受灾点(称为应急需求点，简称需求点)的物资需求不确定条件下，进而考虑最小化应急救援时间和应急救援成本两个目标，解决如何合理地为应急物流中心选址以及相应的物资调运路线及调运量。

这里考虑的应急物流系统，包括了应急物资的收集中心、应急物流中心和应急需求点，在该系统中，首先将应急物资从收集点运送至应急物流中心，再根据实际情况由应急物流中心将应急物资配送至应急需求点；另外，考虑到突发事件可能导致救援道路堵塞或救援道路失效等状况，应急物资也可直接由收集点配送至应急需求点。为更好地构建模型，提出以下假设：(1)不考虑救援物资运输方式的差异，即简化各类应急救援物资的运输，仅考虑单一运输方式(通常为公路运输)，网络节点之间满足车辆运输的可达性；(2)每个应急需求点对各类应急物资的需求量都不超过单个应急物流中心的物资存储量，且均可由车辆统一运输；(3)各类应急物资满足运输的相容性，即不考虑不同应急物资不能同时运输的情况；(4)不考虑运输车辆的工作时间限制和车辆容量限制，假设各个应急物资收集点和应急物流中心拥有足够数量的运输车辆和足够的车辆运载容量。

1.2 符号说明

(1)集合

U：应急物资收集点u的集合；G：应急物资种类g的集合;

I：备选应急物中心i的集合；J：应急物资需求点j的集合。

(2)变量

fi：第i个备选应急物流中心开设的固定成本;

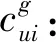
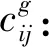
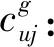
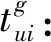
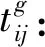
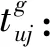
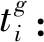
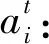
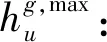
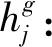
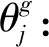
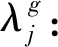
(3)决策变量

zi∈{0,1}：是否在备选应急物流中心i选址决策变量，zi=1表示在应急物流中心i选址，否则zi=0;

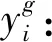
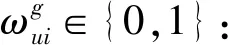
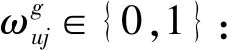
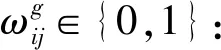
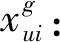
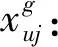
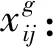
1.3 多目标确定型模型构建

考虑应急物资送达应急需求点的时间和应急物流的总成本，第一个应急救援时间目标包括应急物资在物流中心的周转调配时间，以及应急物资在物资收集点、应急物流中心和应急需求点之间的运输时间；第二个应急救援成本目标主要由应急物流中心的修建成本和运营(存储)成本，以及应急物资在物资收集点、应急物流中心和应急需求点之间的运输成本构成。

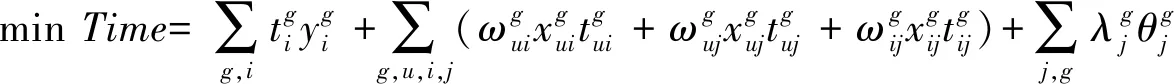
(1)

(2)

(12)

模型中式(1)和(2)为目标函数，式(1)为最小化应急救援时间，包括运输时间和周转时间；式(2)为最小化应急救援成本，包括应急物流中心建设成本、应急物资在应急物流中心的存储成本和应急物资的运输成本。式(3)～(6)为应急物流系统的物资流量守恒条件，其中式(3)和(4)表示应急物流中心处的流量守恒条件，式(5)表示应急需求点处的流量守恒或需求量被满足，式(6)表示物资收集点处的流量守恒或物资收集点处运输出去的各种应急物资不能超过物资收集总量；式(7)表示每个应急需求点的某种物资都仅由一个物流中心或收集点提供物资救援；式(8)表示只有被选为物流中心才能运输物资；式(9)保证每种应急物资的供应能力；式(10)～(12)表示决策变量约束。

1.4 多目标鲁棒优化模型构建

由于突发事件的突发性和很难准确预测性，在应急救援时，除了应急物资可能供应不及时外，还很难对各应急需求点对各种物资的需求做出准确估计，另外应急救援物资的运输成本和运输时间可能出现波动变化。考虑这些不确定性因素，引入问题情景的集合和鲁棒约束系数，在已有变量和决策变量的符号上添加情景s∈S，表示对应情景s∈S下的变量或决策变量。为此，在上述确定模型的基础上，构造多目标鲁棒优化模型如下

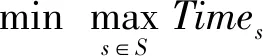
(13)

(14)

(15)

(16)

(28)

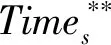
2 模型求解

2.1 多目标的处理

本文模型中，时间目标和成本目标是很难协调一致，而在实际的应急物流救援过程中，对成本和时间的要求也不尽相同，从而两者的重要程度也可能不同。另外，时间的计量单位和成本的计量单位不同，传统的线性加权法不可行。虽然已有文献[39,42]利用百分比无量纲方法(采用固定值100除以目标值)来消除两个子目标计量单位的差异，但该做法存在两个不足，其一是不能真正体现两个目标的计量单位及其数量级差异，其二是无法适应问题数据的变化。为此我们首先将每个情景的两个目标单位消除，计算公式如下

(29)

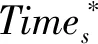
其次我们考虑决策者赋予两个目标的重要程度，设w为决策者根据实际情况赋予成本目标的重要程度值，称为成本偏好权重，满足0≤w≤1。则多目标确定型模型的目标函数(1)～(2)可以转化为下式

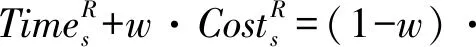
(30)

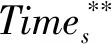
(31)

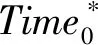
2.2 混合蛙跳算法设计

混合蛙跳算法(Shuffled Frog Leading Algorithm, SFLA)是一种模仿青蛙群体寻找食物的新型仿生物学智能优化算法，由Eusuff et al.[43]为解决组合优化问题而提出。其主要特点是将群体青蛙分成多个子群体，每个子群体都各自执行局部搜索策略，在搜索过程中反复合并青蛙群体和拆分青蛙群体，并在各个子群体之间进行信息交流。由于该算法采用子群体的概念，比其他智能优化方法增加了搜索过程的灵活性和有效性，且能更有效地避免陷入局部最优值。

对于任何一种智能算法而言，问题的编码是至关重要的一环。我们将应急物资需求点的每一种物资所接受的救援服务设施(应急物资收集点和备选应急物流中心)作为编码，即利用应急物资收集点和备选应急物流中心给所有应急物资需求点的各种物资提供的对应救援作为编码。具体来说，假设有m个应急物资需求点，每个应急需求点有n种物资需求，采用符号编码方式，构造一个m×n维的向量(称为青蛙个体或染色体)

X=(x1,…,xn,xn+1,…,x2n,…,xmn)

(32)

其中基因位k的取值xk(1≤k≤mn)表示给对应需求点提供某种应急物资的物资收集点或备选应急物流中心的编号，位置k=(i-1)·n+j对应第i个需求点第j种应急物资。

例如，假设有2个需求点，每个需求点有3种应急物资需求，救援系统中有3个物资收集点(编号为1,2,3)和3个备选应急物流中心(编号为4,5,6)，青蛙个体为(1,4,2,5,4,1)，表示给第一个需求点的三种应急物资提供救援服务的分别是收集点1、应急物流中心4和收集点2，给第二个需求点三种应急物资提供救援服务的分别是应急物流中心5、应急物流中心4和收集点1。

青蛙总群体初始化：根据应急物资需求点数量和应急物资数量，青蛙个体的每个基因位随机生成一个字符，代表给该基因位对应需求点及应急物资提供服务的设施(可能是备选应急物流中心，也可能是应急物资收集点)。

青蛙子群体的划分方式：先将所有青蛙按照适应度从小到大排序，将第一个青蛙划分到第一个子群体，第二个青蛙划分到第二个子群体，依次类推，将第m个青蛙划分到第m个子群体，第m+1个青蛙划分到第m+1个子群体，如此操作，直到所有青蛙都处理完毕。

(33)

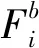
适应度函数：对于多目标确定型模型，我们直接采用式(30)计算；对于多目标鲁棒优化模型，我们采用式(31)计算，若当前个体在某个情景s下不满足鲁棒约束，则对该个体的适应度施加一个大的惩罚项。

本文求解多目标确定型模型和多目标鲁棒优化模型的通用型混合蛙跳算法的流程图参见图1，左图为混合蛙跳算法的主流程，右图为各个子群体进行局部搜索的流程。

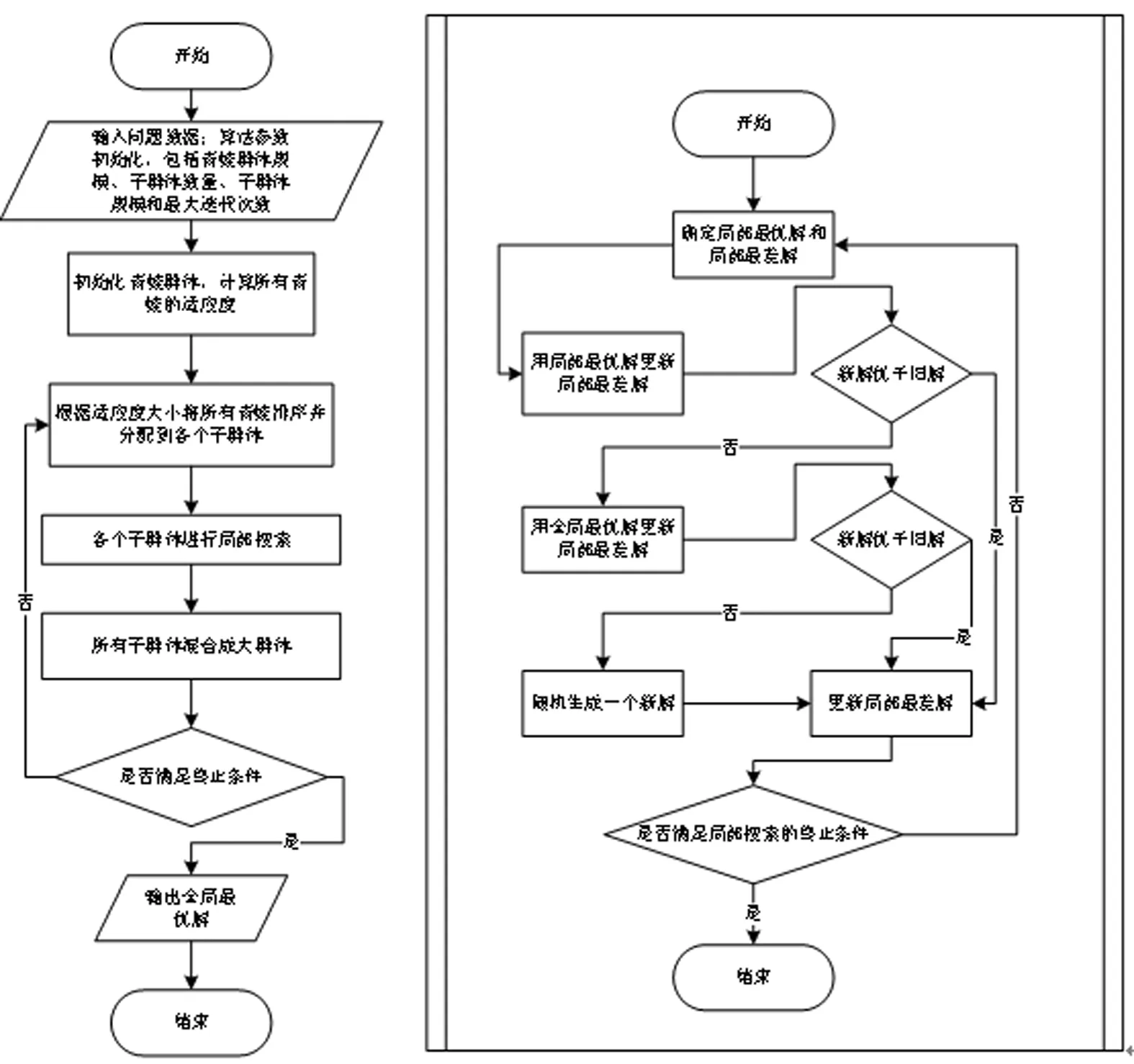
图1 混合蛙跳算法SFLA的流程图(左边为主流程，右边为局部搜索流程)

3 算例分析

3.1 数据描述

已知某应急物流系统有3个应急物资收集点(编号为1,2,3)，3个可供选择的应急物流中心备选点(编号为4,5,6)，以及3个应急物资需求点(编号为7,8,9)和3种应急物资(编号G1,G2,G3)，基准情景下的问题数据如表1～表3[39,42]，另外设置需求点应急物资缺货的单位惩罚系数为280。在基准情景数据的基础上，将需求点的物资需求量、单位运输成本和运输时间附加服从[0,0.2]上的均匀分布随机数的份额，共生成5个情景的问题数据。

表1 备选应急物流中心信息

表2 物资收集点信息

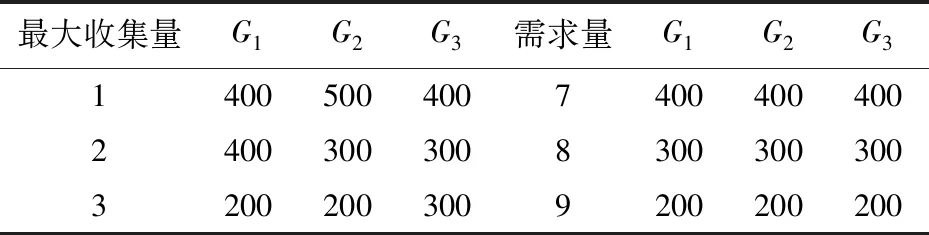
表3 应急物资信息

3.2 结果与分析

求解本文多目标模型的混合蛙跳算法的参数设置为：最大混合迭代次数100，各个青蛙子群体的最大局部搜索次数40，青蛙子群体数目取4，每个青蛙子群体的规模取20。另外，本文设定所有情景下的鲁棒约束系数均相同，即ps=p,∀s∈S。

3.2.1 成本偏好权重的影响分析

首先，为验证多目标确定型模型的有效性，考虑基准情景数据。对成本偏好权重从0至1间隔0.05取值，利用混合蛙跳算法优化求解，给所有需求点各类物资的最佳救援分配方案参见表4。其中最佳救援分配方案2- 4- 6- 6-2-2-5-5- 6表示，第一个需求点的三种应急物资分别由收集点2、应急物流中心4和应急物流中心6提供救援服务，第二个需求点的三种应急物资分别由应急物流中心6、收集点2、收集点2提供救援服务，第三个需求点分别由应急物流中心5、5、6提供救援服务，其余的最佳救援分配方案的含义类似。表4的结果表明，一开始成本偏好权重较低，即决策者在救援时优先考虑应急时间，此时的三个应急物流中心全部开设，以满足初始救援时的时间紧迫性要求；当成本偏好权重逐渐增大(从0.35到0.6)，应急物流中心减少到两个(即应急物流中心5和6选址)；当成本偏好权重进一步增大，决策者优先考虑应急成本时(成本偏好权重从0.65到1)，应急物流中心减少到一个(即应急物流中心4选址)。

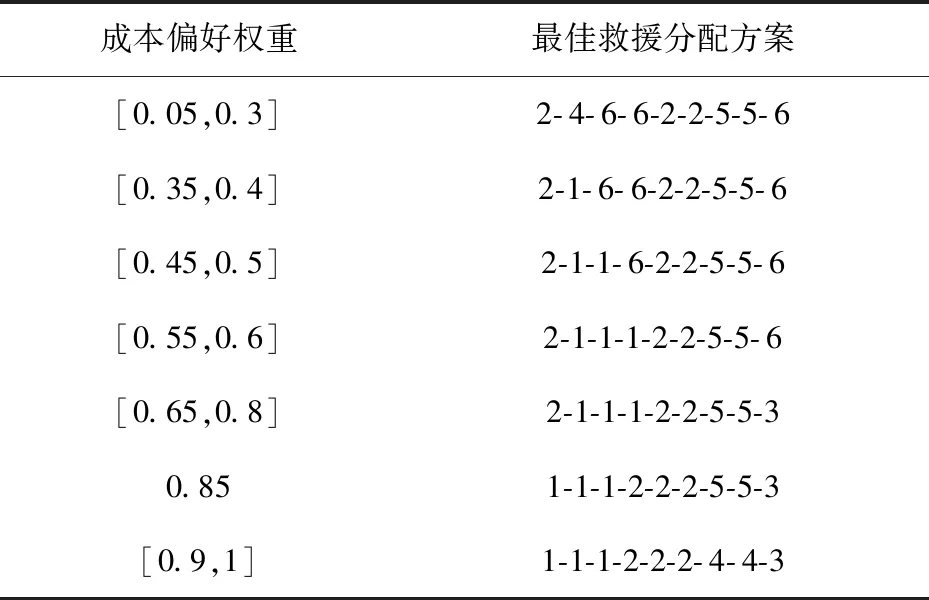
表4 不同成本偏好权重下的最佳救援分配方案

表5 三个成本偏好权重下的最优救援路径和救援物资调运量

表5给出了基准情景在三个成本偏好权重下的救援路径和救援物资调运量结果。当成本偏好权重分别取值0.35、0.55和0.8时，应急救援成本分别为557100、472100和453900，应急救援时间分别为21700、25000和26400。显然，当决策者赋予救援成本不同权重时，应急救援的成本和时间有不同的最优值，不可能达到应急救援成本和时间同时下降的可能，一个子目标的改善很可能会引起另一个子目标变劣。

其次，为进一步分析成本偏好权重和应急救援的关系，尤其是不同的应急救援阶段应如何设置成本偏好权重的问题。图2给出了所有情景的成本和时间的平均值及标准差随成本偏好权重变化的趋势图。表5和图2说明，当决策者赋予成本偏好权重的值越来越大时，救援成本的最优值逐步缩小，但应急救援时间却逐步增大，这与现实的救援情况相吻合；另一方面，成本偏好权重的不同取值可以对应应急救援的不同阶段，应急救援的初期主要考虑高时效性，应急救援成本偏高些也能接受，这可看作对应较小的成本偏好权重的情形(如表5中的0.35情形)；中期救援时，既要考虑时效性又要考虑成本，可看作对应适中的成本偏好权重(如表5中的0.55情形)；后期救援，时效性退居次要地位，主要考虑成本因素，可看作对应较大的成本偏好权重(如表5中的0.8情形)。从图2仔细分析救援成本和救援时间的变化趋势，可初略地将对应的权重分为三个区间段，第一个区间段为[0,0.45]，第二个区间段为[0.45,0.75]，第三个区间段为[0.75,1],三个成本偏好权重的区间段可看作分别对应救援初期、中期、后期或末期。第一阶段的特征是成本偏好权重较低，最优救援时间较小，但救援成本居高不下，符合灾难发生后启动应急救援系统的时间紧迫性要求；第二阶段的特征是成本偏好权重适中，既考虑救援时间的紧迫性要求，又考虑了应急救援系统能承受的成本限制，随着权重的缓慢增加，救援成本急速下降，但所需救援时间急速增加；第三阶段的特征是成本偏好权重很大，此时主要考虑应急救援系统的成本限制，符合应急救援后期或末期的特点，此时成本减少缓慢，时间增加稍快。

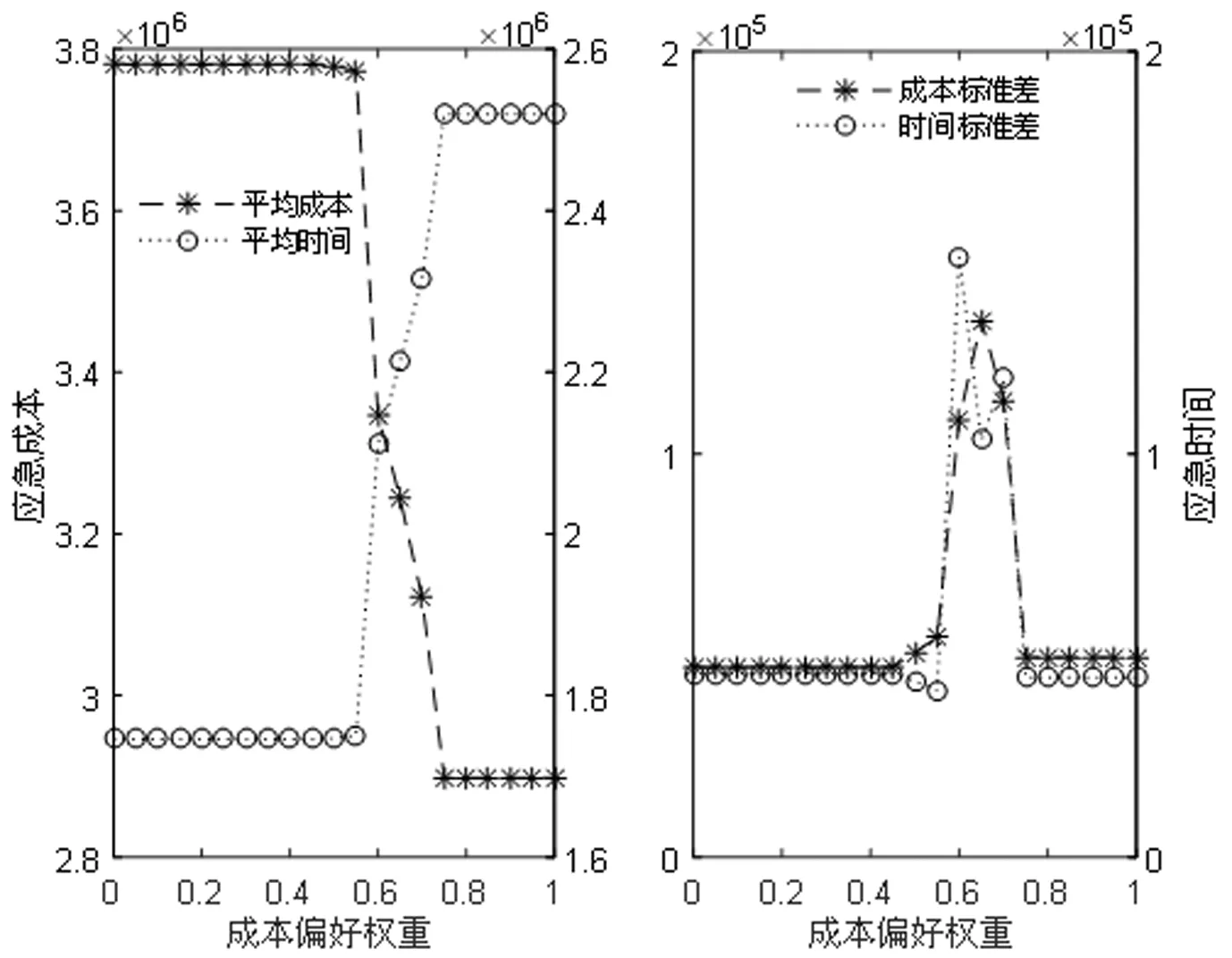
图2 确定型模型均值及标准差的变化趋势

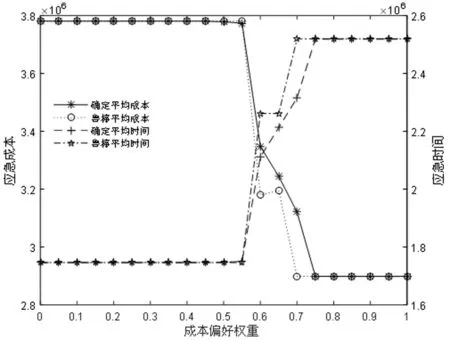
图3 两种模型的平均值变化趋势

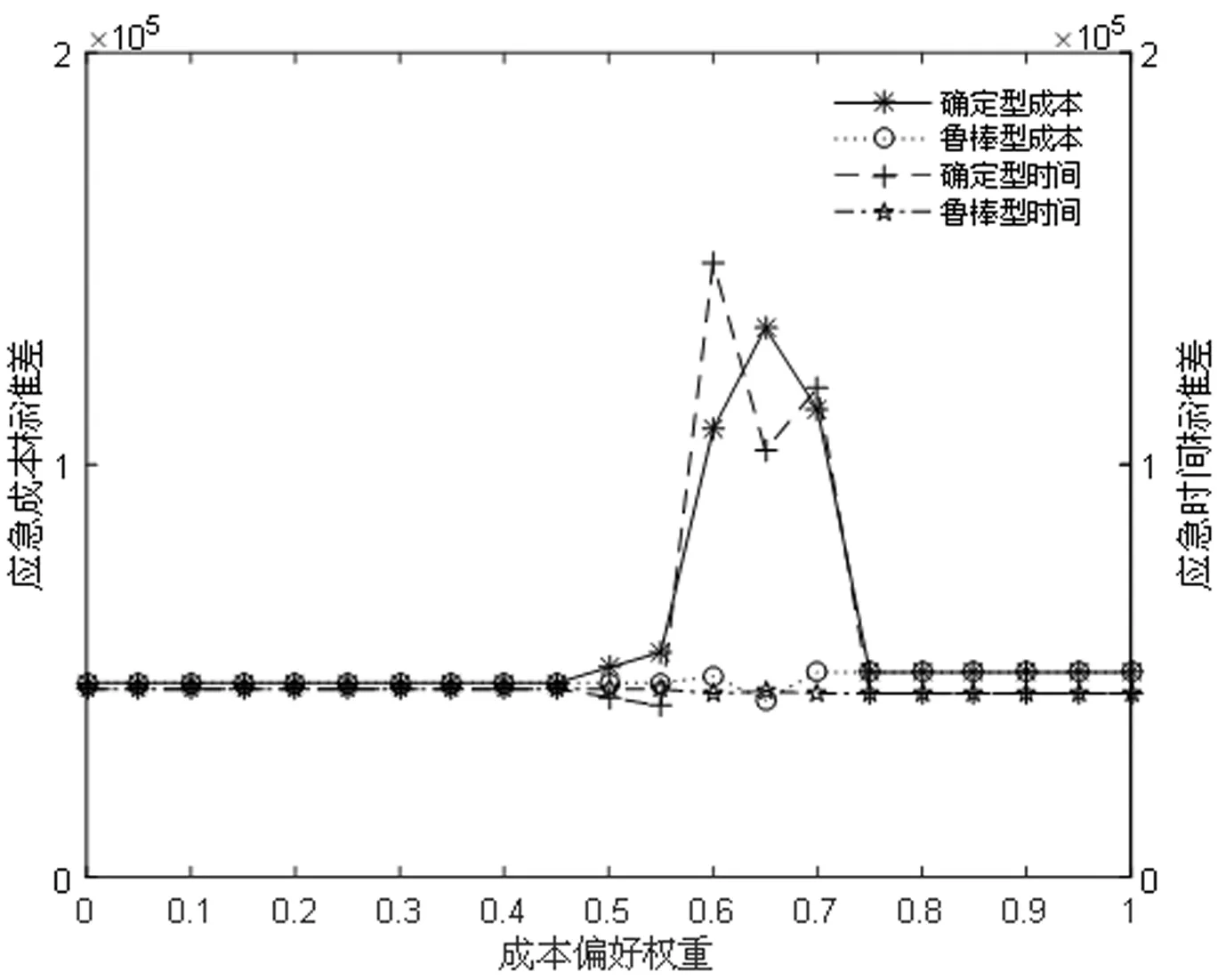
图4 两种模型的标准差变化趋势

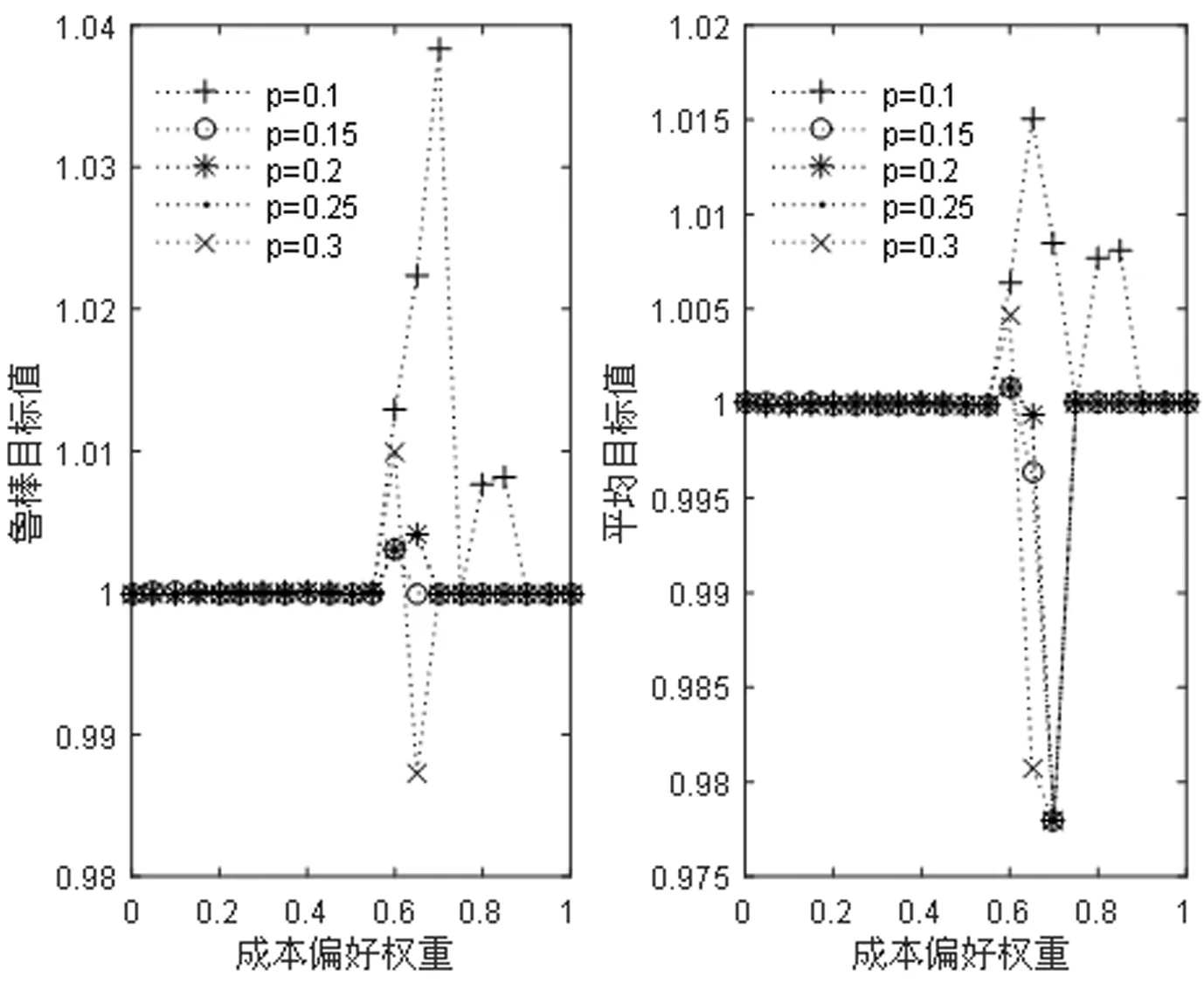
图5 鲁棒约束系数的影响分析

再次，为检验本文多目标鲁棒优化模型和确定型模型的优劣性，我们对所有情景的鲁棒约束系数均取值为0.2。图3和图4分别给出了两种模型的平均值(时间和成本)和标准差(时间和成本)随成本偏好权重变化的趋势图。图3的平均值结果仅能初略地看到，当成本偏好权重取值于[0,0.55]和[0.75,1]时，两种模型的差别并不大；但当成本偏好权重取值于[0.6,0.7]时，确定型模型的平均成本明显高于鲁棒优化模型的平均成本。然而，当我们关注图4给出的两种模型的标准差(时间和成本)时，可以发现，确定型模型的两种标准差都比鲁棒优化模型的标准差大；尤其，当成本偏好权重取值于[0.55,0.7]时，确定型模型的标准差比鲁棒优化模型的标准差高出一倍左右。这说明，鲁棒优化模型具有较好地应对各种不确定性的抗干扰能力。具体来说，从总趋势看，鲁棒模型对应的成本偏好权重也可分为三个区间段，第一个区间段为[0,0.45]，第二个区间段大致为[0.45,0.75]，第三个区间段大致为[0.75,1]，三个成本偏好权重的区间段可看作分别对应救援初期、中期、后期。

根据图表给出的结果和前面的讨论，我们可以考虑将应急救援划分为三种类型，时间紧迫性较强的救援初期、兼顾救援成本的救援中期以及注重救援成本的救援后期，决策或建模优化求解时可选择不同的成本偏好权重，这里根据上述讨论将成本偏好权重的取值范围区分为[0,0.45]、[0.45,0.75]和[0.75,1]，也可以单一取值，如0.35,0.55和0.8等。

3.2.2 鲁棒约束系数的影响分析

为了考察不同的鲁棒约束系数的影响，我们分别了考虑五种不同的鲁棒约束系数取值，即取值为0.1,0.15,0.2,0.25,0.3，图5给出了多目标鲁棒优化模型在不同鲁棒约束系数下获得的鲁棒目标值(左图)以及所有情景在当前鲁棒最优解下的平均目标值(右图)。这里的平均目标值的含义是，给定鲁棒约束系数下可获得最优鲁棒解，该鲁棒解又对应着各个情景下的目标值，计算这些目标值的平均值。从图5可以看到，当成本偏好权重在[0,0.45]和[0.75,1]内取值时，不同鲁棒约束系数下的鲁棒目标值和平均目标值都非常稳定；另外，注意到当成本偏好权重在[0.75,1]内取值且鲁棒约束系数全部取0.1时，鲁棒目标值和平均目标值都有较大的波动，这说明鲁棒系数较小(即给定鲁棒要求比较严格)时，找到一个鲁棒最优解比较困难，甚至在极端的情形可能找不到一个满足所有情景的可行解。当成本偏好权重在[0.5,0.75]内取值时，不同的鲁棒约束系数有不同的影响，当鲁棒要求较严格(鲁棒系数取0.1)时，鲁棒目标值随着成本偏好权重的增大迅速增大；当鲁棒要求较宽松(鲁棒系数取0.3)时，鲁棒目标值上下波动；当鲁棒要求一般(取值0.15到0.25)时，鲁棒目标值相对比较平缓。根据上述分析，我们推荐在鲁棒优化中鲁棒约束系数在[0.15,0.25]内取值，或者取其中值0.2。

4 结束语

本文考虑特发事件，尤其是自然灾害发生后，如何启动应急救援系统进行应急救援行动，考察了应急物流中心选址以及相应的物资调运路线及调运量问题，将受灾点(需求点)的物资需求量、运输成本和运输时间不确定因素纳入范畴，以总救援成本最小化和救援时间最小化为目标建立了确定型多目标应急物流中心选址模型和多目标应急物流中心选址的鲁棒优化模型，为将双目标转化为单目标并考虑问题数据数量级变动等因素，构建了利用单目标下最优值转化双目标的方法，该方法也适合更多目标函数的情形。为有效求解这两个模型，设计了一种通用的混合蛙跳算法，并用算例验证了模型和算法的有效性。根据求解结果，我们讨论了不同成本偏好权重的影响和不同鲁棒约束系数的影视，并给出了应急救援不同阶段下的成本偏好权重的设置规则和鲁棒约束系数的推荐取值。

但是本研究也存在不足之处，例如实际应急物流中心选址中还可能要考虑交通方式的差异、救援道路的路况或中断因素、物资运载工具的多寡及容量约束、不同救援阶段应急物资收集的价格因素等，这些将是进一步研究应急物流中心选址的可行方向。