基于聚类矩阵近似的协同过滤推荐研究

张 文, 崔杨波, 李 健, 陈进东

(1.北京工业大学 经济管理学院,北京 100124; 2.北京化工大学 经济管理学院,北京100029; 3.西安文理学院 信息工程学院,陕西 西安 710065; 4.北京信息科技大学 经济管理学院,北京 100101)

0 背景介绍

随着Web 2.0技术和电子商务的不断发展，互联网上充斥了海量的在线商品和服务的信息，使得网络用户获取自己所需在线商品的成本不断提升。为筛除无关信息以解决用户信息过载问题，协同过滤方法被提出并被应用于在线商品推荐系统以根据用户画像向其推荐可能感兴趣的商品[1]。一般来说，可将协同过滤方法分为两种：基于最近邻的协同过滤方法和基于矩阵分解的协同过滤方法[2,3]。前者通过用户之间与商品之间的邻近关系来为用户推荐新的商品[3,4]；后者将用户-商品评分矩阵分解为用户潜在偏好向量与商品潜在特征向量并利用二者之间的内积来预测用户对于商品的评分[2,3]。

近年来一系列基于矩阵分解的协同过滤推荐方法被提出并得到了学术界和工业界的一致认可。2006年Netflix Prize电影推荐竞赛的结果表明了基于矩阵分解的协同过滤方法SVD++(Singular Value Decomposition++)要优于传统的基于最近邻的方法。SVD++方法将用户-商品评分矩阵中隐含的附加反馈信息、个体行为信息与整体行为信息统一整合在了一起，因此其预测效果相比基于最近邻的协同过滤方法要好[1]。尽管基于矩阵分解的协同过滤方法表现较好，但在实际的协同过滤的应用中，还存在以下两方面问题亟需解决。

第一方面的问题来自于用户-商品评分矩阵的稀疏性[5]。推荐系统中存在巨量的用户和巨量的商品，然而巨量的用户往往仅对少量的商品进行评分，这就导致用户-商品评分矩阵中产生大量的评分缺失数据，即评分矩阵稀疏性。评分矩阵稀疏性将会导致无法准确度量用户与用户、商品与商品之间的相似性，因此也会降低对用户-商品推荐的准确性。第二方面的问题来自于传统推荐方法的计算可扩展性[6]。已有的基于矩阵分解的协同过滤方法大多直接采用线性代数方法或者概率统计方法来分解整个用户-商品评分矩阵以得到用户潜在偏好向量与商品潜在特征向量。然而，当面对巨量的商品和用户时，对于用户-商品评分矩阵的分解将变得难以计算[7]。

对于第一方面的用户-商品平均矩阵稀疏性的问题，研究人员聚焦于如何通过缺失修复方法利用估算值去填充矩阵中评分为零的元素，从而消除矩阵中评分为零的元素，然后在此基础之上利用填充后的矩阵进行协同过滤推荐[8]。Xia等人[9]利用均值填充(Mean Imputation)方法，将用户未评分的商品赋以所有其它评分的平均值，然后使用填充后的数据进行商品协同过滤。Gong[10]采用基于案例推理方法CBR(Case-based reasoning)方法来填补空缺的评分，其基本思想是，对于一个具有商品评分缺失值的用户，首先利用欧式距离锁定与其相似用户的集合，然后根据相似用户的在对应商品上的评分来估算该缺失的商品评分。

对于第二方面的计算可扩展性问题，研究人员重点关注如何利用高效的线性代数和概率抽样计算方法从观测到的用户-商品评分矩阵元素中抽取出用户潜在偏好向量和商品潜在特征向量[8]。Chen和Peng[11]借鉴概率矩阵分解PMF(Probabilistic Matrix Factorization)的思想，认为现实的评分矩阵R中的数据叠加产生于两个高斯分布随机矩阵：一是商品是否对用户进行了展示的隐性反馈数据；二是用户对所展示商品的真实评分数据。前者通过用户潜在因素矩阵U与商品展示潜在因素矩阵Z之间的乘积得到；后者通过用户潜在因素矩阵U与商品评分潜在因素矩阵V之间的乘积得到。为计算上述的U矩阵，矩阵Z和矩阵V，他们对用户已经评分(Positive正类)数据进行抽样和未评分的(Negative负类)缺失数据进行随机抽样和概率推导，并由此提出了PMF+P+N(PMF with Positive and Negative feedbacks)方法。Xue等[12]利用深度学习方法对用户-商品评分矩阵R进行分解，并提出了深度矩阵分解方法DMF(Deep Matrix Factorization)。其基本思想是利用矩阵的行向量pui作为学习用户偏好潜在向量的输入，并同时利用矩阵R的列向量作为学习商品特征潜在向量qgj的输入。之后，以pui，qgj的内积与用户ui在商品qj上的评分rij之间的差距RMSE(Root Mean Square Error)作为损失函数以进行深度学习用户偏好潜在向量pui和商品特征潜在向量qgj。

为了解决上述推荐系统中的数据稀疏性和计算可扩展性问题，本文提出了一种基于聚类矩阵近似的方法CF-cluMA(Collaborative Filtering based on Clustered Matrix Approximation)以用于协同过滤。CF-cluMA方法首先对用户-商品评分矩阵分别进行用户(行)聚类和商品(列)聚类，将具有相似评分的用户和商品在矩阵中的位置重新排列，以形成新的矩阵块。然后，通过设定稠密阈值参数，CF-cluMA利用对稠密矩阵块实施奇异值分解(Singular Value Decomposition，SVD)和对各个稠密矩阵块奇异向量进行施密特正交化来重新近似原始的用户-商品评分矩阵。最后，利用近似后的用户-商品评分矩阵预测用户对商品的未知评分。一方面，CF-cluMA方法在计算过程中采用稠密矩阵块，降低了数据的稀疏性。另一方面，CF-cluMA方法在计算过程中同时对多个较小规模的稠密矩阵块实施奇异值分解以近似原始用户-评分矩阵，提高了矩阵分解方法的计算可扩展性。在EachMovie公开数据集上的实验表明，与现有的基于矩阵计算的协同过滤方法相比较，CF-cluMA方法无论在推荐的准确性还是计算复杂度方面都能得到较好的结果。

1 问题描述

(1)

2 基于聚类矩阵近似的协同过滤方法—CF-cluMA

在当前的电商平台上不同的用户对于不同商品的兴趣各不相同，因此构成了对于在线商品消费的不同群体，形成了用户-商品的局部特性。大多数的用户仅关注电商平台上一小部分的商品，而大量的商品仅被少部分用户所关注。在协同过滤推荐系统中，用户与用户、商品与商品之间存在群体划分，在不同的用户群体内部，他们对商品群体的偏好并不相同。CF-cluMA的基本思想正是利用了在线用户对于在线商品的局部兴趣，将原始的大规模的用户-商品评分矩阵进行聚类分块近似以提高协同过滤的计算准确性并降低计算复杂程度。CF-cluMA方法主要分为三个步骤：首先对用户-商品评分矩阵进行用户(行)聚类和商品(列)聚类以形成分块矩阵；然后对稠密分块矩阵逐个实施奇异值分解，并对奇异向量进行施密特全局正交化以近似原始用户-评分矩阵；最后利用近似后的矩阵进行商品评分预测。

2.1 用户聚类和商品聚类

CF-cluMA方法采用了经典的矩阵谱聚类方法[13]来对用户-商品评分矩阵中的用户和商品实施聚类。在谱聚类中，给定用户-商品评分矩阵R，构造无向图N=(V,E)。其中V={1,2,…,|V|}是顶点的集合，代表商品和用户；E={eij|如果边{i,j}存在}是边的集合，表示用户和商品之间的评分关系；每条边的权重为Eij，即用户ui对商品gj的评分。在推荐系统中，用户与用户、商品与商品之间不存在关联，因此在用户集合和商品集合内部不存在边，仅在单个用户ui对单个商gj品有评分行为时存在边，由此定义用户-商品的邻接矩阵M如式(2)，此时用户-商品的邻接矩阵M可以表示为式(3)。

(2)

(3)

在给定的用户-商品评分矩阵R中寻找特定的用户群所关心的特定的商品类别需要对用户群体和商品群体进行同时聚类，也就是对用户-商品评分矩阵R同时实施行聚类和列聚类。假设用户聚类个数为c1，商品聚类个数为c2，不相关的用户聚类集合可表示为{Ui|Ui∈U,1≤i≤c1}。同理，不相关的商品聚类集合可表示为{Gj|Gj∈G,1≤j≤c2}。对于给定一个用户聚类集合Ui，如果其对应的商品聚类为Gj，那么这就意味着在对评分矩阵R实施聚类后的分块矩阵上，用户聚类集合Ui和商品聚类集合Gj所对应的矩阵分块构成了一个稠密矩阵块。Ui和Gj定义如公式(4)和公式(5)所示。

(4)

从式(4)和式(5)可以看出，商品的聚类集合影响着用户的聚类集合，反过来，用户的聚类集合也影响着商品的聚类集合。可以证明，最优的商品与用户聚类集合在上述图模型取最小割时取得[13]，即:

(6)

其中，v1,…,vk是上述无向图G图中任意的k个聚类。

为求得上述图N模型的最小割，首先定义用户-商品的拉普拉斯矩阵L，如式(7)所示。

(7)

根据以上定义可得L=D-M。其中M是邻接矩阵，D是对角“度”矩阵，Dii=∑keik。根据谱图聚类模型[13]，当广义特征值问题Lz=λDz获得求解时的第二大特征值对应的广义特征向量即为图中每个点的聚类表示向量，其中z为广义特征向量，L和D分别由式(8)和式(9)分别表示。

(8)

(9)

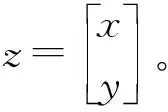
(10)

假设D1和D2均为非奇异阵，那么式(10)可展开为式(11)和式(12)。

(11)

(12)

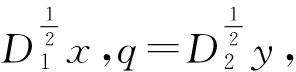
(13)

(14)

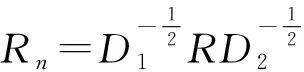
(15)

P(2,l+1)向量中的每行元素按顺序代表原始矩阵R中行的位置，Q(2,l+1)向量中的每行元素按顺序代表原始矩阵R中列的位置。之后，利用K-Means方法[15]对向量Z2进行聚类。最后，按照P(2,l+1)向量与Q(2,l+1)向量在聚类中的位置对原始评分矩阵R重新按行和按列排列以得到各个聚类对应的分块矩阵。

2.2 矩阵近似

根据聚类结果重新调整评分矩阵R中用户和商品的位置，使得属于同一聚类的商品和用户聚集在一起，形成新的评分矩阵R′。其具体表现形式为，原始评分矩阵R上给出了相似商品相似评分的用户以及对应的商品聚集在一起，使得新的评分矩阵R′的某些块评分比较密集，形成稠密矩阵块，而剩下的不在聚类中的矩阵块则较为稀疏。重新聚类后的评分矩阵R′的分块矩阵形式(其中Rij为矩阵块)如式(16)所示。其中，[Rij]表示稠密矩阵块，其余为稀疏矩阵块。

(16)

在式(16)的基础之上，借鉴Savas[16]等人提出的聚类矩阵近似方法，对谱聚类后形成的稠密分块矩阵进行矩阵近似，如式(17)所示。

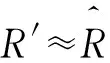
(17)

(18)

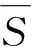
Pi=orth([Pi,c1i,j,…,Pi,c1i,|CIi|]),

(i,c1i,1),…,(i,c1i,|RIi|)∈RIi

(19)

Qi=orth([Qc2j,1,j,…,Qc2j,|CIj|,j]),

(c2j,1,j),…,(c2j,|RIj|,j)∈CIj

(20)

2.3 聚类矩阵近似协同过滤推荐

(21)

从上述计算过程可以看出，CF-cluMA方法相比于最初的SVD方法的优点包括两个方面。一方面，因为对原始用户-评分矩阵R做了聚类处理，使得矩阵中相似的部分可以重新排列在一起，原始大规模矩阵的内在结构得到了局部优化。这一优点正好对应可推荐系统中用户与商品的分群结构特点，即推荐系统中存在潜在用户群体和潜在商品群体。另一方面，由于新的用户-商品评分矩阵R′中的稠密矩阵块Rij的秩远远小于原始矩阵用户-商品评分矩阵R的秩，因此使得矩阵计算的复杂度大大降低，提高了计算的效率。除此之外，由于CF-cluMA方法只考虑新的用户-商品评分矩阵R′中的稠密矩阵块而不考虑稀疏矩阵块，使得协同过滤推荐系统能够充分利用已知的用户对于商品的真实评分数据而较少将未知缺失数据纳入推荐考虑范围，减少了未知的确实数据对于推荐结果的干扰。

2.4 算法复杂度分析

3 实验验证

3.1 实验数据及实验设置

本文的实验数据来自经典的EachMovie数据集[17]，它包括了72916个用户对1628部电影的评分数据，共计2811983条数据。评分数据分为六个等级，分别为0，0.2，0.4，0.6，0.8和1.0。为了便于计算，本文在实验时对评分进行了转换，将六个等级由低到高分别转换为1，2，3，4，5和6。同时为了保证数据的有效性，本文在实验时剔除了一些极端数据。数据剔除标准为用户评分数量小于3的电影和电影评分少于4个的用户。经过上述预处理之后，本文将EachMovie数据集转化为一个2584行1140列的用户-电影评分矩阵，其行代表用户，列代表电影。

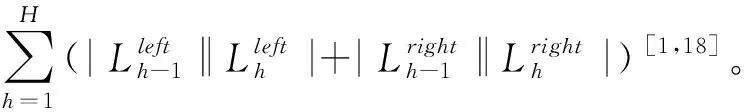
3.2 推荐系统性能评价指标

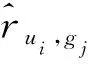
(22)

3.3 实验验证

本文使用EachMovie数据集行进实验，在对数据进行剔除和整理后，生成了一个2584x1140的用户-电影评分矩阵。本文应用MATLAB软件进行编程实现了CF-cluMA算法，并将该评分矩阵的数据实进行了可视化。

图1与图2分别展示了该评分矩阵在进行谱聚类前后的数据分布特征，图中横轴表示电影数量，本实验中共1140部电影；纵轴表示用户数量，本实验中共2584个用户。图中NZ(none zero)表示矩阵中非零元素的个数，通过计算得出该矩阵的稠密度为3.36%，稠密矩阵块展现了特定用户群体与特定电影群体之间的强关联性，体现了用户-电影评分矩阵的内在局部结构。在通过参数设置对评分分块矩阵完成主导性稠密矩阵块筛选后[16]，CF-CluMA方法在这些主导性稠密矩阵块内进行矩阵近似，并采用公式(21)进行商品评分预测。

图1 用户-电影评分矩阵数据分布图

本文在进行实验时取90%的数据作为训练数据集，10%的数据作为测试数据集。为保证实验结果的可靠性，本文采用10次10折交差验证法。将推荐数据集随机均分划分为10等份，在每次的试验中利用其中的9份作为训练数据进行矩阵聚类近似，而取剩下的1份数据进行预测评分测试。在本实验中取聚类个数为10，主导性稠密矩阵块的阈值δ=20%，即每次将评分矩阵块中非零数据密度小于20%的矩阵块过滤掉，剩下的矩阵块为主导性稠密矩阵块。评分近似矩阵中矩阵块的秩取1到10，针对不同的秩进行实验。最后，利用公式(22)计算基于聚类矩阵近似的预测评分准确度，实验结果如表1所示。同时，当为CF-cluMA方法设置不同秩的时候，其计算所需要消耗的时间(以秒计)也不相同，具体结果如表2所示。

表1 CF-cluMA方法评分预测准确度RMSE

表2 不同秩条件下的CF-cluMA方法的计算消耗时间(单位：秒)

3.4 对比实验

在目前的推荐系统领域，主流的协同过滤算法包括SVD++[1]，PMF+P+N[11]和DMF[12]。在对比试验中，SVD++方法的秩分别取为5，10，15和20。DMF方法的降维向量长度D分别取为5，10，15和20。PMF+P+N方法的向量维数分别取值为5，10，15和20，迭代次数t为20。表3和表4分别展示了对比实验中SVD++，PMF+P+N和DMF方法的预测RMSE评分准确度和计算所消耗的时间(以秒计)。

通过对比实验可以看出，SVD++方法的预测评分准确度与CF-cluMA方法的预测评分准确度比较接近，DMF方法的预测评分准确度效果次之，PMF+P+N方法的效果最差。总体上，SVD++方法和CF-cluMA模型的准确度较高。对于CF-cluMA方法，当其秩取1到8时，准确度平均高于SVD++方法(超过4%)。而当秩的设置大于等于9时，SVD++方法的准确度较高，其可能解释是，当秩取1到8时，较小的秩使得SVD++和CF-cluMA模型损失掉了一些信息。然而，CF-cluMA方法在对非稠密矩阵块进行矩阵近似时采用的是主导性稠密矩阵块奇异向量的正交化后的奇异向量，可以捕捉到大量的矩阵局部信息，因而准确度较高。当秩逐步增大超过8以后，对原始矩阵的近似程度越来越来高，局部结构的特点不再格外明显时，SVD++方法的准确度要高于CF-cluMA方法。对于DMF方法和PMF+P+N方法，当它们取秩较小的时候，其性能可以被显著地改善。但是，其效果依然比本文所提出的CF-cluMA方法差。

表3 对比方法的预测评分准确度RMSE

表4 对比实验组计算所消耗的时间(单位：秒)

在计算复杂度方面，DMF方法计算复杂度最低，耗时最少。PMF+P+N方法次之，SVD++方法随着秩的增加，计算复杂度也随之急剧增加。CF-cluMA方法的计算耗时是最少的，而SVD++，PMF+P+N和DMF方法的耗时均较高，而对比预测准确度较高的SVD++方法，其每次计算所需消耗的时间至少是CF-cluMA方法的十倍以上。而且，随着秩的增加，SVD++方法的消耗时间成指数级增长。因此本文认为，尽管CF-cluMA方法和SVD++方法的预测评分误差相对较小，但是前者的计算耗时较少。因此，从总体上来说，本文所提出的CF-cluMA方法要优于SVD++方法。

4 结论

本文针对推荐系统协同过滤方法中存在的数据稀疏性、可扩展性差问题提出了新的解决方法，即基于聚类矩阵近似的协同过滤推荐方法CF-cluMA。CF-cluMA方法借助于历史用户-商品评分数据进行评分预测，它通过对数据进行聚类，识别数据的内在局部结构，形成分块矩阵，并借助于稠密分块近似进行用户-商品评分预测。该方法有三个优点：一是通过在分块矩阵内部进行矩阵分解，达成了降低计算数据维度的目的；二是通过在分块矩阵内存进行预测推荐提升了推荐系统的可扩展性，降低了推荐系统的复杂度；三是在分块矩阵内进行推荐降低了不必要数据的干扰性，提高了推荐系统的预测评分准确性。与其它方法相比较，本文所提出的CF-cluMA方法的预测评分准确率高于DMF方法与PMF+P+N方法，与SVD++方法接近，并且在秩较小时优于SVD++方法。本文所提出的CF-cluMA方法的复杂度也小于现有的DMF方法、PMF+P+N方法和SVD++方法。在未来的工作中，本文将进一步研究如何选取商品和用户同时聚类个数的参数优化，同时在矩阵分解中进一步考虑用户-商品隐式评分和用户实时行为[20,21]，以期实现更好的推荐效果。