精确覆盖问题的加权分治算法

胡 沁， 宁爱兵， 苟海雯， 张惠珍

(上海理工大学 管理学院,上海 200093)

0 引言

精确覆盖(exact cover, EC)及其各种变形问题在运筹学、管理学、组合数学和计算机科学等领域被广泛研究，例如针对阵列雷达子阵划分问题[1]，该问题可做如下简单概述：阵列雷达可分为许多子阵，然而囿于器件水平、系统成本及工程实现难度等因素的限制，每一子阵对区域的覆盖范围不同，其范围类似于若干个多联六边形组成的非规则形状。为了保证预警探测、空间监视等军事任务的安全性，在阵列雷达设计时，不仅需要保证对阵面全覆盖而且需要降低工程实现的难度，如何做到只用特定非规则形状的子阵对整个阵面进行精确覆盖是达到这一目标的核心问题。除此之外精确覆盖在信息科学[2]、自动化系统设计[3]、通信工程[4]及密钥管理[5]等诸多领域亦具有非常广泛的应用，因此精确覆盖问题具有极其重要的研究价值和意义，也是组合优化中经典的NP-Hard问题，除非P=NP，否则不存在多项式时间算法。

目前求解精确覆盖问题的算法主要分为精确算法和启发式算法。Donald Knuth在2000年首次提出了解决精确覆盖问题的精确算法——X算法[6]，但随着问题的规模和元素总个数的增加，求解问题的时间越来越长，随后有许多学者开始尝试改良X算法以加快求解速度[7]。近年来，大量学者开始尝试运用启发式算法求解精确覆盖问题，并取得了令人满意的结果，如量子算法[8]、绝热量子算法[9]、DNA计算机算法[10]、基于光学原理的算法[11]等。启发式算法的优点在于能够快速得到问题的可行解，但无法确保所得到的解是问题最优解。

分支降阶技术由Davis和Putnam提出，是解决NP难题最常用的方法，其核心思想是先通过降阶规则对问题规模进行约减，再将简化后的问题通过分支规则分解成若干小规模的子问题进行求解。加权分治技术由Fomin、Grandoni和Kratsch提出[12,13]，目前基于加权分治技术的精确算法的设计和分析被广泛应用于求解NP-Hard问题中[14～17]，以期获得最优解的同时，降低算法的时间复杂度，其核心思想是根据问题中某个对象的重要程度来设置不同数值的权值，比如图论中的某些问题可以根据图中结点的度来设置每个结点的权值，结点的度不同，那么结点权值也可能不同，最后再以图中结点的权值之和作为问题的规模，而不是像传统方法以结点的个数作为问题的规模。以权值之和作为问题的规模能更加精确的描述原问题以及分支子问题规模的大小，达到降低精确算法时间复杂度的目的。

本文首先给出了EC问题的定义，问题的数学性质及其证明；接着根据定义和数学性质设计出基于分支降阶的回溯算法，并利用传统分析方法对算法进行分析得出时间复杂度为O(1.4656k)；然后采用加权分治技术根据EC问题的不同特征设置相应的权值，以权值之和作为问题的规模对算法进行时间复杂度分析，把该算法的时间复杂度降为O(1.3842k)；最后对算法进行对比分析并对全文内容加以总结。

1 问题介绍及性质

1.1 精确覆盖问题简介

F为集合X的若干个子集构成的集合，若存在F的一个子集F*，满足X中的元素有且仅有一次包含在F*的一个元素中，那么称F*为X的一个精确覆盖。上述定义中，F*中任意两个元素交集为空且F*中所有元素并集为X。精确覆盖问题是找出这样的一种覆盖F*，或证明其不存在。

如果F中存在集合为空集，那么该集合是否存在于精确覆盖中没有任何区别，因此通常假定：F*中的任一集合都至少包含一个元素，也就是说规定F中的空元素都不在精确覆盖集合F*中。

1.2 问题转换

在算法处理之前，本文把精确覆盖问题转换成二分图来进行处理，转换方法如下：

将精确覆盖问题中X的每个元素作为二分图的一个元素子集X，把F中的每个元素作为二分图的一个集合子集F，F中的元素是集合。若F中的元素fi包含X中的元素xi，则在fi与xi之间连线，否则不连线。

这样处理后，得到一个图G=(V,E)，其中V=X∪F，E={(x,f)|x∈X,f∈F且x∈f}。很显然，图G是二分图。而原问题的求解变为在集合子集F中找出若干子集的集合F*，使得元素子集X中的每一个元素与F*中的元素有且仅有一条边相连。

1.3 数学符号

为了方便描述，采用如下数学符号表示：

N(v)：结点v的开邻集，即与结点v之间存在一条边的点的集合；

N[v]：结点v的闭邻集，即N[v]=N(v)∪{v}；

d(v)：结点v的度，即与结点v相关联的边的数目；

m：表示二分图元素类X中的结点个数；

n：表示二分图集合类F中的结点个数；

X：X={xi|i=1,2,…,m}，X为问题介绍中的集合X，X中共有m个元素；

F：F={fj|j=1,2,…,n}，F为问题介绍中的集合F，F中共有n个元素；

F0：F0为F的子集且F0中任一元素在精确覆盖F*中则不能取得可行解，也就是说F中不能出现在精确覆盖F*中的元素就放入到F0中；

F1：F1为F的子集且F1中任一元素不在精确覆盖F*中则不能取得可行解，也就是说F中一定出现在精确覆盖F*中的元素就放入到F1中；

FF0：对于集合F中的结点fi，在回溯算法分情况时假设其不在精确覆盖F*中，则将其加入集合FF0；

FF1：对于集合F中的结点fi，在回溯算法分情况时假设其在精确覆盖F*中，则将其加入集合FF1；

g(fi)：表示结点fi与Ffi中元素交集不为空的元素个数，也就是说Ffi中有g(fi)个元素集合与fi的交集不为空；

H(fi)：表示集合Ffi中与fi存在交集的结点集合，也就是说H(fi)是Ffi的最大子集且H(fi)中的每个元素与fi的交集都不为空。

1.4 递归算法时间复杂度的通用公式

设基于分支降阶的递归算法得到如下的递推公式：T(n)=T(n-t1)+T(n-t2)+…+T(n-tr)，其中n为原问题的规模；(n-t1),(n-t2),…,(n-tr)分别为第1,2, …,r个子问题的规模。

令T(n)=xn，则上述递推式可以转化为求方程xn=xn-t1+xn-t2+…+xn-tr的唯一或者最大解。设方程唯一或者最大解为α，则该算法在最坏情况下的时间复杂度为O(αn)。该方法的详细信息参见文献[12]。

1.5 数学性质

性质1在集合子集F中，若存在一结点fi且d(fi)=0，则结点fi必定不在精确覆盖集合中。

证明由d(fi)=0可知，结点fi为空集，根据前面精确覆盖问题的规定，结点fi必定不在精确覆盖集合F*中。

性质2在元素子集X中，对于X中的任一结点xi，若d(xi)=0，则问题无解，即不存在可行解。

证明若d(xi)=0，则说明xi无法被集合子集F中的任何元素覆盖，问题显然无解。

性质3在集合子集F中，对于任意两个结点f1和f2，若N(f1)=N(f2),则可以将f1和f2中的任一结点及其关联边从图中删除。

证明由于结点f1和f2在二分图中起到的作用完全相同，因此根据精确覆盖问题的性质，两者取其一即可满足。

性质4在集合子集F中，若任意结点fi都满足d(fi)≤1，则该问题可以在多项式时间内解决。

证明根据性质1可以去掉集合F中所有度为0的结点，由于集合F中所有结点的度都小于等于1，所以之后只剩下度为1的结点，再利用性质3可以去掉覆盖元素相同的结点，则二分图中剩下的fi和xi之间必定是一一对应的关系，显然问题可以在多项式时间内解决。

性质5若集合子集F中存在一结点fi,g(fi)=0且结点fi不为空集，那么结点fi必定在精确覆盖集合中。

证明根据性质1，可以把d(fi)=0的结点从集合F中移除，之后集合F中的任一结点fi，都有d(fi)≥1，g(fi)=0说明结点fi与集合F中的其它任何结点都不存在交集，那么N(fi)中的元素只能由结点fi来覆盖，因此结点fi一定在精确覆盖集合中，否则N(fi)中的元素无法被覆盖。

性质6在元素子集X中，若存在一结点xi且d(xi)=1，那么覆盖xi的结点fi一定在精确覆盖集合中。

证明根据精确覆盖问题的定义，显然成立，否则xi无法被覆盖。

性质7在二分图中，若结点fm是集合子集F中g(fi)值最大的结点，如果此时g(fm)≤1，则问题可在多项式时间内求解。

证明由性质5可以去掉所有g(fi)=0的结点，因为g(fm)≤1，那么之后集合F中任一结点fi的g(fi)值都等于1，不妨设与结点fm存在交集的结点为ft，再根据性质6可以去掉必定在精确覆盖集合中的结点，此时图中仅剩下一种情况即N(fm)=N(ft)，根据性质3可以去掉两者之中任意一个结点。集合F中其它结点也可以这样处理，因此此时问题可以在多项式时间内解决。

2 算法设计及复杂性分析

2.1 精确覆盖问题的求解算法

在前面数学性质的基础上，设计如下求解算法：

Step1初始化：输入图G，集合X，集合F，此时F0={}，F1={}，FF0={}，FF1={};

Step2根据性质1，若在集合子集F中存在度为0的结点fi，那么该结点一定不在精确覆盖中，F0=F0∪{fi}，F=F{fi}，同时从图中删除结点fi；

Step3根据性质3，若在集合子集F中存在N(f1)=N(f2)的两个结点f1和f2，则可以将两者之中任一结点加入集合F0，同时将该结点从集合F中移除，并将该结点及其相关联的边从图中删除；

Step4根据性质5，若图G中存在一结点fi且g(fi)= 0，则F1=F1∪{fi}，F=F{fi}，同时从图中删除结点集N[fi]及其相关联的边；

Step5根据性质6，如果图G中存在结点xi∈X且d(xi)=1，N(xi)=fi，则F1=F1∪{fi}，F=F{fi}，同时从图中删除结点集N[fi]及其相关联的边，F0=F0∪H(fi)，F=FH(fi)，并将H(fi)中的结点及其相关联的边从图中删除；

Step6利用前面的数学性质1到性质6对问题进行降阶处理之后分两种情况：(1)由性质7得到问题的最优解，则算法结束；(2)还无法得到问题的最优解，则跳到Step 7；

Step7k=|F|；调用回溯子算法Backtrack(1)。

回溯子算法Backtrack(i)描述如下：

Step1若i>k，说明搜索到达叶子结点，此时对应一个可行解，即得到一个精确覆盖集合F1∪FF1，检查F1∪FF1是否覆盖元素子集X中的所有元素，如果满足条件，回溯子算法Backtrack(i)结束；若i≤k，则跳到Step 2；

Step2利用二叉树来搜索最优解，其过程为：从集合F中取出g(fi)值最大的结点fm，对结点fm分下面步骤中的(1)和(3)两种情况处理，具体步骤如下：

(1)情况1：假设结点fm在精确覆盖集合中，令局部集合变量temp0={}，temp1={}，此时检查(F1∪FF1∪F)H(fm)是否覆盖元素子集X中的所有元素，若不能覆盖，说明这种情况下没有可行解，则剪枝，不进入左子树，并跳到下面的(3)去尝试进入右子树；若能覆盖，说明这种情况下有可行解，此时temp1=temp1∪{fm}，FF1=FF1∪{fm}，F=F{fm}，在二分图中删除结点集N[fm]以及其相关联的边，temp0=temp0∪H(fm)，FF0=FF0∪H(fm)，F=FH(fm)，并将H(fm)中的结点及其相关联的边从图中删除；利用性质1到性质6对于集合F中的结点进行降阶处理，若结点fi必定在精确覆盖集合中，那么temp1=temp1∪{fi}，FF1=FF1∪{fi}，F=F{fi}，temp0=temp0∪H(fi)，FF0=FF0∪H(fi)，F=FH(fi)；若结点fi必定不在精确覆盖集合中，此时temp0=temp0∪{fi}，FF0=FF0∪{fi}，F=F{fi}；按上述方法处理之后，若集合F中没有结点，则整个算法结束；否则，调用回溯子算法Backtrack(i+1)进入左子树；

(2)返回二叉树上一层前恢复FF0=FF0 emp0、FF1=FF1 emp1和F=F∪temp0∪temp1；

(3)情况2：假设结点fm不在精确覆盖集合中，令局部集合变量temp0={}，temp1={}，此时检查(F1∪FF1∪F){fm}是否覆盖元素子集X中的所有元素，若不能覆盖，说明这种情况下没有可行解，则剪枝，不进入右子树，结束回溯子算法Backtrack(i)；若能覆盖，说明这种情况下有可行解，此时temp0=temp0∪{fm}，FF0=FF0∪{fm}，F=F{fm}，在二分图中删除结点fm及其相关联的边。利用性质1到性质6对于F中的结点进行降阶处理，若结点fi必定在精确覆盖集合中，那么temp1=temp1∪{fi}，FF1=FF1∪{fi}，F=F{fi}，temp0=temp0∪H(fi)，FF0=FF0∪H(fi)，F=FH(fi)；若结点fi必定不在精确覆盖集合中，此时temp0=temp0∪{fi}，FF0=FF0∪{fi}，F=F{fi}；按上述方法处理之后，若集合F中没有结点，则整个算法结束；否则，调用回溯子算法Backtrack(i+1)进入右子树；

(4)返回二叉树上一层前恢复FF0=FF0 emp0、FF1=FF1 emp1和F=F∪temp0∪temp1。

算法结束后，集合F1∪FF1即是精确覆盖问题的一个最优解。

2.2 传统方法分析时间复杂度

传统分析方法以二分图集合子集F中结点的个数k来分析算法的时间复杂度。T(k)为搜索树产生的叶子结点个数，其中k在求解算法中的Step 7中定义为k=|F|，则该算法有如下递推公式：

T(k)=T(k-1)+T(k-3)

(1)

其中T(k-1)代表被选中的结点fm不在精确覆盖集合中，此时在图中仅删除结点fm，因此问题规模减少1；T(k-3)代表被选中的结点fm在精确覆盖集合中，因此在二分图中删除结点fm，并将H(fm)中的结点一并删除，由算法及性质7可知与结点fm存在交集的结点集H(fm)中的元素个数大于等于2，因此问题规模至少减少3。

根据1.4节介绍的方法求解T(k)，即求方程x3=x2+1在1与2之间的最大解，解得x≈1.4656，因此T(k)=1.4656k,由此可以得出采用传统方法得到的时间复杂度为O(1.4656k)。

2.3 加权分治方法的时间复杂度

为了降低该算法的时间复杂度，下面采用加权分治方法来分析该算法在最坏情况下的时间复杂度。

与前面传统分析方法不同，加权分治方法不是以集合F中结点的个数k作为问题的规模，而是首先给集合F中的每个结点赋予一个小于等于1的权值，然后以集合F中所有结点的权值之和W作为问题的规模来进行时间复杂度分析，具体操作步骤见下面的介绍。

从算法的操作可以看出，该算法的时间复杂度主要与g(fi)的个数有关，因此可以根据g(fi)的个数设置相应的权值，显然对于g(fi)值越大的结点所赋予的权值应该越大，具体如下：

(1)对于g(fi)=0的结点，设置权值为：h0=0；

(2)对于g(fi)=1的结点，设置权值为：h1=0.65；

(3)对于g(fi)=2的结点，设置权值为：h2=0.95；

(4)对于g(fi)≥3的结点，设置权值为：h≥3=1；

设Δh=hi-hi-1，其中i≥1。

为了方便计算二分图中集合子集F的权值之和W，设二分图集合子集F中权值为hi的结点个数为ki，则W的计算公式如下：

W=0.65×k1+0.95×k2+k≥3≤k

(2)

该算法中的关键步骤是Step 7中的回溯子算法，设n1，n2，n≥3分别为H(fi)中g(fi)值分别为1，2和大于等于3的结点的个数，例如n2表示H(fi)中g(fi)值为2的结点个数。

下面分析在回溯子算法中两种不同的情况下问题规模W的减少量：

分支1结点fm在精确覆盖集合中，此时将结点fm以及与fm存在交集的集合H(fm)从图中删除，此时整个问题的规模减少量为C1, 其计算公式为:

C1=0.95+0.65×n1+0.95×n2+n≥3

(3)

在公式(3)中，0.95表示结点fm自身的g(fm)对应的权值，因为g(fm)≥2，因此权值至少为0.95；0.65×n1代表H(fm)中g(fi)=1的结点的总权值；0.95×n2代表H(fm)中g(fi)=2的结点的总权值；n≥3代表H(fm)中g(fi)≥3的结点的总权值。

分支2结点fm不在精确覆盖集合中，此时将结点fm从图中删除，H(fm)中所有结点的g(fi)值都减少1，此时整个问题的规模减少量为C2，其计算公式为:

C2=0.95+(0.65-0)×n1+

(0.95-0.65)×n2+(1-0.95)×n3

(4)

在公式(4)中，0.95表示结点fm自身的g(fm)对应的权值，因为g(fm)≥2，因此权值至少为0.95；(0.65-0)×n1代表删除fm后H(fm)中原来g(fi)=1的结点的权值减少量；(0.95-0.65)×n2代表删除fm后H(fm)中原来g(fi)=2的结点的权值减少量；(1-0.95)×n3代表删除fm后H(fm)中原来g(fi)=3的结点的权值减少量；当i≥4时，总有Δh=0。

因此，以集合F中所有结点权值之和W作为问题的规模来分析时间复杂度，有如下递推公式：

T(W)=T[W-(0.95+0.65×n1+0.95×n2+n≥3)]+

T[W-(0.95+0.65×n1+0.3×n2+0.05×n3)]

(5)

下面分情况来分析该递推方程的时间复杂度。

情况1当g(fm)=1时，由性质7可知，其时间复杂度为多项式时间。

情况2当g(fm)=2时，此时n≥3=0，我们可以根据公式(5)分情况来计算该算法的时间复杂度，计算过程及结果如表1所示。

表1 g(fm)=2的结点进行分支的递推式

由表1可知，情况2下最坏的时间复杂度为O(1.3842w)，由于w≤k，因此情况2下最坏的时间复杂度为O(1.3842k)。

情况3当g(fm)=3时，此时n>3=0，我们可以根据公式(5)分情况来计算该算法的时间复杂度，计算过程及结果如表2所示。

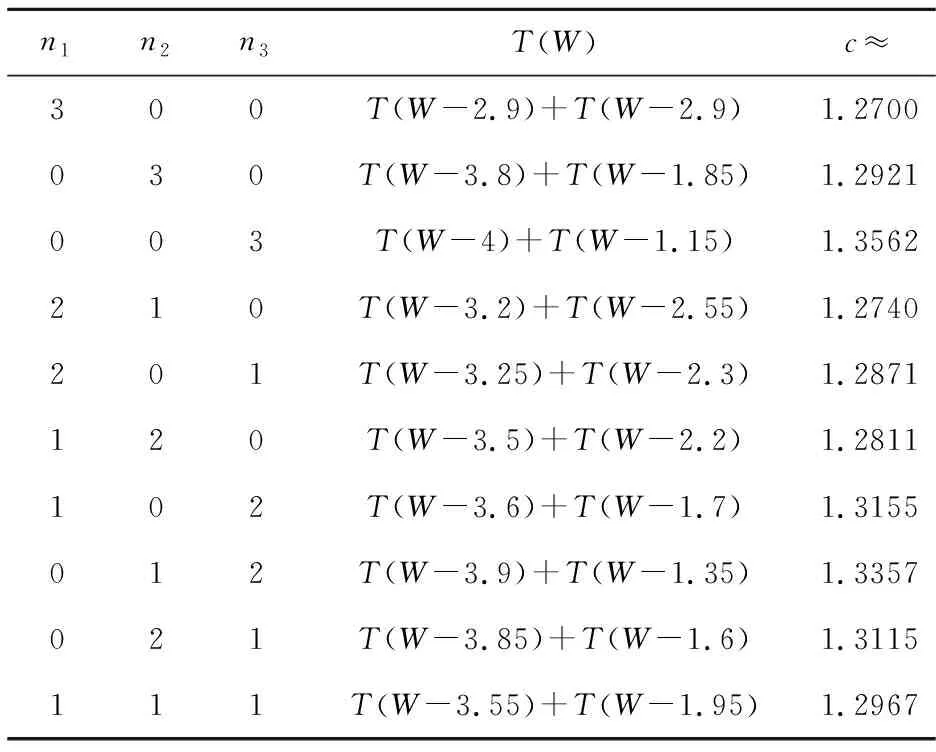
表2 g(fm)=3的结点进行分支的递推式

由表2可知，情况3下最坏的时间复杂度为O(1.3562w)，由于w≤k，因此情况3下最坏的时间复杂度为O(1.3562k)。

情况4当g(fm)≥4时，最坏情况下的时间复杂度递推公式如(6)所示：

T(W)=T(W-1)+T(W-5)

(6)

根据传统方法计算可得T(W)=O(1.3247k)，此时不采用加权分治方法计算。

综合4种情况可知，该算法在最坏情况下的时间复杂度为O(1.3842k)，而在不采用加权分治方法情况下的时间复杂度为O(1.4656k)。

由于算法的比较分析需要用到下面介绍的示例，因此下面先介绍示例分析，然后再给出本文算法与其它精确算法的对比分析。

2.4 示例分析

为了更清楚的说明算法原理及实际应用情况，下面给出一个小规模示例进行说明。

【示例1】如图1所示，现有8个候选集散中心与10个待覆盖区域，由于运营成本和交通运输条件的限制，每个集散中心覆盖若干个区域，若集散中心fi能覆盖待覆盖区域j，那么fi与待覆盖区域j之间连一条边，为了降低经营成本，现从所有候选集散中心中选取若干个，使得区域全覆盖，并且使集散中心之间没有重复覆盖的区域。集散中心与待覆盖区域由二分图来表示，如图1所示。

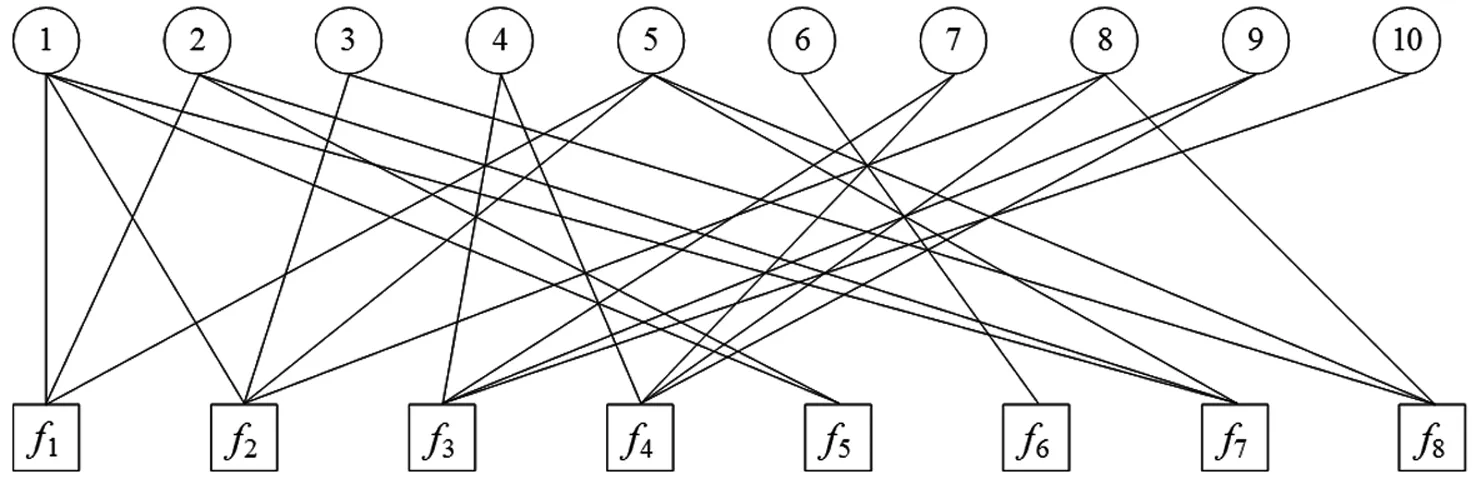
图1 集散中心与待覆盖区域示例图

对上述问题的计算过程可描述如下：

(1)根据性质3，移除结点f1，从二分图中删除结点f1及N[f1]并且删除其相关联的边；

(2)根据性质5，结点f6必定在精确覆盖集合中，将结点f6加入集合F1，从二分图中删除结点f6及N[f6]并且删除其相关联的边；

(3)根据性质6，结点f3必定在精确覆盖集合中，将结点f3加入集合F1，H(f3)={f4},结点f4一定不在精确覆盖集合中，将结点f4加入集合F0，从二分图中删除结点f3和f4及N[f3]并且删除其相关联的边；

(4)根据数学性质降阶处理后，问题的规模如图2所示，此时问题变为在降阶后的集合F中寻找若干个集散中心覆盖剩余5个待覆盖区域。

(5)进入回溯子算法，求解所有可行解的处理过程如图3所示，图3圆圈中的数字表示对应子树的问题规模(以结点的个数为问题的规模)。为了方便叙述，我们设fi=1表示将fi放入精确覆盖集合中，fi=0表示不将fi放入精确覆盖集合中。

具体过程如下：

①首先计算集合F中所有结点的g(fi)值，从中取出g(fi)值最大的结点f2，g(f2)=3，假设结点f2在精确覆盖集合中，检查发现(F1∪FF1∪F)H(f2)不能覆盖所有区域，说明这种情况下没有可行解，剪枝，进入右子树；

②假设结点f2不在精确覆盖集合中，检查发现(F1∪FF1∪F){f2}可以覆盖所有区域，说明这种情况下可能有可行解，接着利用性质1到6对问题进行处理，根据性质5，结点f8一定在精确覆盖集合中，又因为H(f8)={f7},结点f7一定不在精确覆盖集合中；

③继续调用回溯子算法向下一层搜索，集合F中仅剩下结点f5，此时假设结点f5在精确覆盖集合中，到达叶子结点，检查发现F1∪FF1覆盖所有区域，回溯子算法结束。{f3,f5,f6,f8}即是该问题的一个最优解。若结点f5不在精确覆盖集合中，则不能覆盖所有区域。

示例1采用本文算法时，由于利用数学性质缩减了问题的规模，降低了算法的时间复杂度，因此搜索树只有3个分支。

下面以图4为例来说明加权分治方法的原理和分析过程，图4圆圈中的数字表示对应子树的问题规模(以结点的权值之和为问题的规模)。

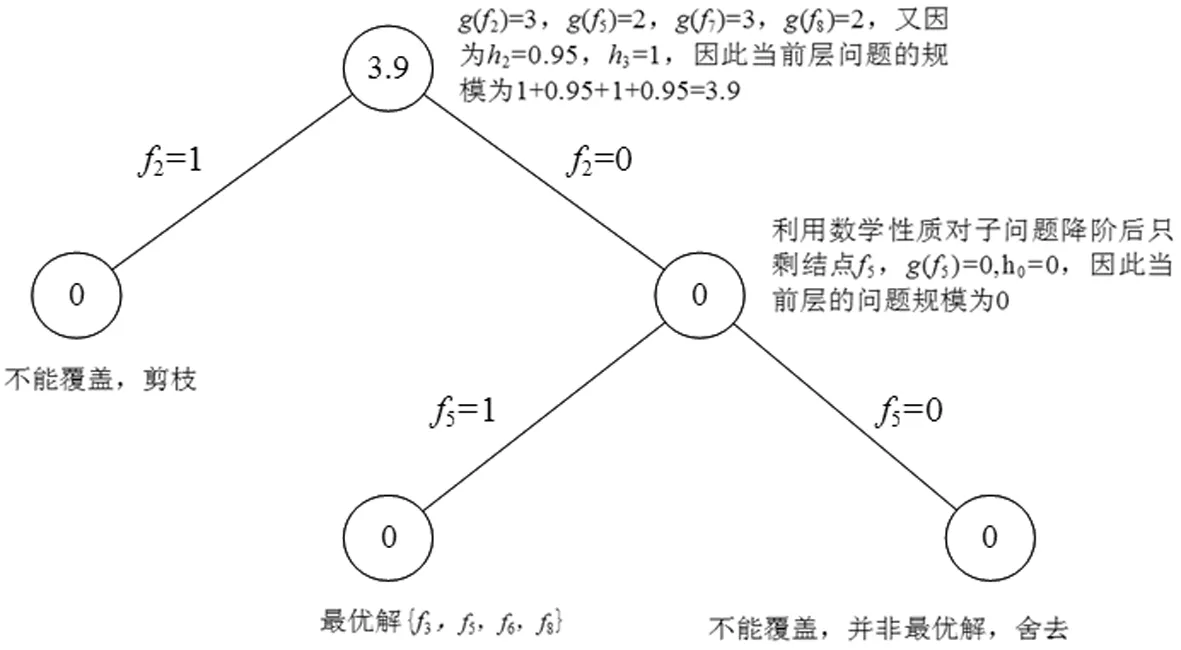
图4 加权分治技术处理后的搜索树

3 与其它算法的对比分析

近年来，国内外研究精确覆盖问题主要有两种方式：启发式算法和精确算法，启发式算法可以快速得到可行解，但是无法保证所得解为最优解，也不能提供解的近似比，因此得到的解往往比精确算法的解要差。

精确算法的比较一般从最坏情况下的时间复杂度、具体示例的叶子结点个数(叶子结点个数等同分支数量)、算法软件求解具体示例的计算时间等3个方面进行比较，其中第1个方面的比较是最重要的，因为这个从理论上保证了即使碰到某算法最难求解的具体示例,其理论的计算工作量也会小于最坏情况下的时间复杂度。X算法是目前求解精确覆盖问题最常用的算法，该算法的详细情况参见文献[1]，下面分别从上述3个角度对本文算法与X算法进行比较分析。

3.1 时间复杂度比较

设T(k)为X算法搜索树产生的叶子结点个数，其中k为集合子集F中结点的个数，则该算法的递推公式如(7)所示：

T(k)=T(k-1)+T(k-2)

(7)

其中T(k-1)代表被选中的结点fi不在精确覆盖集合中，此时仅删除结点fi，因此问题规模减少1；T(k-2)代表被选中的结点fi在精确覆盖集合中，此时删除结点fi，由于与结点fi存在交集的结点个数至少为1个，所以问题规模至少减少2。

由1.4节的通用递推公式得T(k)=1.6181k，由此可以得出X算法的时间复杂度为O(1.6181k)。

本文算法使用了加权分治技术，由前面的分析可知，在最坏情况下的时间复杂度为O(1.3842k)。

当集合数量为k时，X算法在最坏情况下的时间复杂度为O(1.6181k)，也就说此时搜索树中最多有1.6181k个分支；本文算法在最坏情况下的时间复杂度为O(1.3842k)，也就说此时搜索树中最多有1.3842k个分支；由于当k>0时，1.3842k<1.6181k，所以对于最坏情况下的分支数，本文算法是小于X算法的。例如，当k=20时，X算法的分支数最多可能有1.618120≈15140，而本文算法的分支数最多可能有1.384220≈667，667远小于15140。因此，求解同一个算例时，在最坏情况下，本文算法产生的分支数远小于X算法的分支数。

3.2 具体示例的分支数量比较

具体示例分支数量的比较以前面的示例1为例，本文算法的分支数量见2.4节图3。

X算法对示例1求解所有可行解的处理过程的二叉树如图5所示：

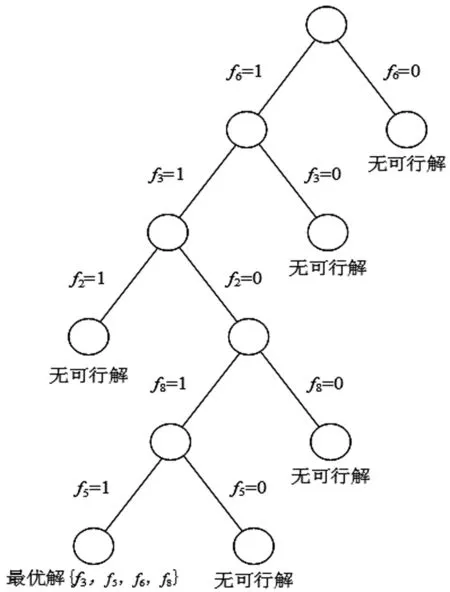
图5 解空间的搜索树

在图3和图5中，每个叶子结点对应一个分支，由图3可知，本文算法共有3个分支，由图5可知，X算法共有6个分支；由此可知，两个精确算法求解该示例时，本文算法的分支数小于X算法的分支数。

3.3 算法软件包求解实例对比

为了比较2个精确算法对具体实例的计算时间和分支数量，采用C++编程实现本文算法和X算法，在CPU为Intel Core i5- 4210M 2.6GHz，内存为4.00GB的计算机上进行试验。下面在表3中给出2个算法对一组随机问题实例的计算时间和分支数量，其中集合数量为n，待覆盖元素个数为m。

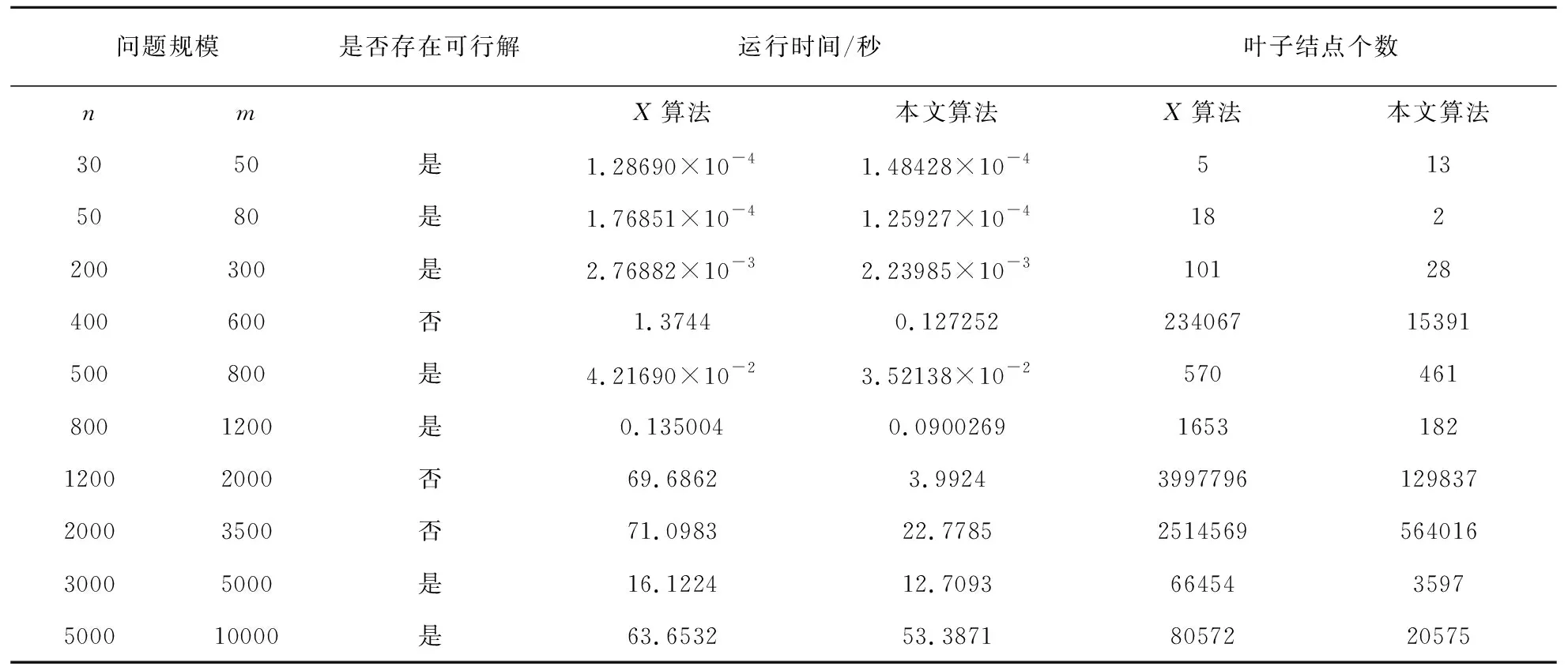
表3 求解时间和分支数量

上述实验表明：在小规模算例中，本文算法的求解时间稍慢于X算法，分支数量也稍多于X算法，因为在小规模算例中，搜索策略与数学性质的作用效果甚微且需要耗费比较多的时间。随着问题规模的增大，搜索策略与数学性质的优势逐渐凸显，因此对于大多数大规模问题实例，本文算法的求解时间和分支数量都优于X算法。

本文算法编写的程序运行时间与集合数量m有较大的关系，测试的结果表明，在一般情况下，集合数量在5000以内时，大多数算例都可以在一个小时内求解。

4 结论

本文针对精确覆盖问题，首先研究该问题的数学性质，利用数学性质对问题进行降阶，缩小问题的规模，这些数学性质不仅能用到本文的算法设计中，而且可以用到精确覆盖问题的其它各种算法设计中，达到加快算法执行速度或提高算法求解效果的目的；然后根据数学性质设计出一个基于分支降阶的回溯算法求解该问题；最后在不改变算法本身的情况下，分别运用常规技术和加权分治技术分析该算法的时间复杂度。分析的结果表明运用加权分治技术得到的时间复杂度相对于常规分析更加精确，使算法的时间复杂度从O(1.4656k)降低到O(1.3842k)，从而获得了更好的效果。文章最后通过与其他精确算法的对比分析，表明本文介绍的精确算法不仅在理论上具有优势，而且在大多数大规模实例求解中具有计算时间少的优点。