基于成本效益分析的救护车多时段布局优化研究
蒋清宸, 苏 强, 祝延宏, 王秋根
(1.同济大学 经济与管理学院,上海 200092; 2.上海市第一人民医院,上海 200080)
0 引言
院前急救(Emergency medical service, EMS)是指紧急事故发生时,病患拨打急救电话,急救中心派遣救护车及相应设备人员到达现场进行医疗救护的过程[1]。院前急救作为城市医疗卫生体系和公共安全应急保障体系的重要组成部分,在维护市民健康和保障城市安全方面发挥重要的作用。世界卫生组织(WHO)的统计数据显示,对危重病人实施急救的黄金时间是5分钟,一旦超出10分钟,病人的生还概率将显著降低达80%以上,因此救护车对急救需求的响应时间十分关键。根据Lowthian等[2]的预测,到2020年随着全球老龄化的趋势加剧,对急救服务的需求将会上升46%~69%。这无疑对现有有限急救资源的优化管理提出了更紧迫的要求。
救护车布局对院前急救的效果与效率有着重要影响。对于救护车布局问题,可从规划和运营两个层面来考虑:(1)规划层面的救护车布局问题常利用静态模型对站点的选址以及车辆分配进行决策,以达到预期的覆盖范围、响应时间、急救资源数量等目标。(2)运营层面的救护车布局问题则进一步在动态环境中,考虑在需求、行驶速度、救护车的不可获得性等不确定因素影响下救护车的布局。
尽管研究救护车配置布局问题的文献众多,但大多数研究集中于规划层面,目标是最大化急救服务覆盖范围。本文属于运营层面的研究,重点研究在时变环境下的救护车布局问题。同时考虑院前急救的服务水平及其经济性指标。引入成本-效益分析,根据随时间变化的需求、行驶速度以及救护车可获得性,调整车辆规模与布局方案,在保证急救服务水平的基础上,降低急救社会总成本。
本文在理论建模基础上,应用2014年上海市松江区的急救数据进行实证分析,利用改进的蚁群算法计算分析了各种情况下的优化方案。结果表明在保证急救服务效果的前提下,优化后的系统比原系统的社会总成本下降32.23%;相比于静态优化模型,考虑时变因素的模型可以使EMS社会总成本降低15.8%,同时能够显著提升各时段救护车辆的工作负荷平衡度。
1 文献综述
救护车布局问题的研究已经开展40多年,从研究角度可分为两大类:静态环境下救护车规划层面的研究,和动态环境下救护车运营层面的研究。
早期的最具代表性的静态环境下的救护车布局模型是Toregas等[3]提出的LSCM(Location set covering model),该模型的优化目标是在覆盖所有需求点的情况下最小化救护车的数量。另一个早期代表性模型是Church和ReVelle[9]提出的Maximal Covering Location Problem (MCLP),是在给定的救护车资源限制下最大化需求覆盖。在这些经典静态研究基础上,近期静态环境下规划层面的研究开始考虑多种需求类型(Liu等[4])、多种救护资源类型(Soo-Haeng等[5])、多阶段救护(Liu和Yang[6])等因素对救护车布局的影响效果。
经典静态模型没有考虑救护车的不可获得性及由此导致的某些需求点的伪覆盖问题。为了来克服这一缺陷,Gendreau[10]提出了双覆盖模型(Double Standard Model, DSM),使需求点被救护车多次覆盖,当一辆救护车执行任务无法响应其他需求时,需求点仍有备选救护车可及时响应需求。DSM模型保证α%的需求量在高标准时间r1内被覆盖,并且所有需求点在低标准时间r2内被救护车至少覆盖一次(r1 一些研究已经开始在动态的环境中考虑救护车运营层面布局的问题。Repedeand J Bernardo[13]将Daskin[11]提出的Maximum Expected Covering Location Problem(MEXCLP)拓展成多时段的MEXCLP模型,以最大化各时间点的期望覆盖范围为目标函数,考虑了行驶时间、需求分布和救护车规模等随时间变化因素的影响。Rajagopalan等[15]提出的在动态的需求环境中的多时段模型,进一步考虑了救护车可获得性的不确定性。在满足预设的救护车可获得率的同时,最小化救护车数量。Schmid[16]提出了多时段的mDSM模型,考虑了行驶速度在时间和空间分布上的变化,最大化所有时段总的双覆盖范围。该模强调行驶速度和再布局惩罚系数对各时段车辆布局和再布局的影响,但是忽略了需求在不同时段的变化。Pieter L等[7]对多时段的研究也主要关注行驶速度随时间的变化,最大化期望覆盖范围的同时,最小化再布局车辆数,忽略了需求与车辆规模在不同时段的变化,可能导致在需求低的时段过度配置救护资源。 现有的动态环境中的研究,大多以最小化救护车数量或者最大化覆盖范围为目标优化车辆布局,难以在急救效果和救护资源的悖反中达到均衡。在考虑随时间变化的因素上,许多研究并未同时考虑需求、行驶速度以及救护车可获得率的影响。基于此,本文在双覆盖DSM模型的基础上引入成本效益分析,在考虑需求、行驶速度以及救护车不可获得率随时间变化的影响下,分时段优化救护车布局。其余部分结构如下:第二节建立多时段的救护车优化布局模型,对院前急救系统进行成本效益分析;在第三节,根据多时段模型的特点设计了启发式算法。第四节应用上海市松江区的实际数据,对提出的模型和算法进行实证分析。最后是结论与展望。 模型的目的是为所有的时间段t∈T(T={1,2,…,n},在候选的救护车站点中决定站点配置的救护车数量,从而使救护车能在低标准时间r2内到达所有的需求点,并且保证α%(0<α<1)的需求量能被救护车在高标准时间r1(r1 模型中符号定义如下: 表1 符号定义 建立模型如下: minf(x)=∑t∈T(CsttNstt+CamtNamt+ (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) 上一部分建立的多时段救护车布局模型是一个NP-hard问题,难以在有限的时间和资源限制下得出精确解,因此本文设计了启发式算法寻求该问题有效的近似最优解。在经典的蚁群算法的基础上,根据多时段救护车布局模型的特点设计算法求解。 由于多时段模型的求解规模远远大于单一时段的求解规模,直接利用蚁群算法编码多时段的解会使计算规模呈指数增长,可能降低解的精确性,因此本文结合贪婪算法的思想,利用蚁群算法寻求每一时段的最优解,再通过对时段循环迭代得到最优解。通过对比验证,贪婪思想结合蚁群算法求解的结果明显由于蚁群算法直接编码的求解结果。算法具体设计如下。 蚁群算法应用在上述问题中时,每只蚂蚁代表一个解,即一个救护车的布局方案,其搜索过程如下:在初始时刻,m只蚂蚁被放置在起始救护车备选站点上,每只蚂蚁随机选择该站点上的救护车数量。其次,蚂蚁k(k=1,2,…,m)按照随机比例选择下一个救护车备选站点中停放的车辆数。救护车可能数量的信息矩阵的初始值是相同的,因此,初始的信息矩阵定义为μij(0)=μ0,其中i表示放置的救护车数量,j表示备选的救护车站点。蚂蚁选择站点中停放车辆的概率为: 式中,μij表示(i,j)上的信息素;ηij表示(i,j)上的启发因子,其初始值相同;S表示备选站点的集合。 为了保证所有的救护车备选站点都被蚂蚁访问,采用禁忌表来记录蚂蚁k在每个备选站点上选择的车辆数。每只蚂蚁k代表一个车辆布局方案。当所有蚂蚁完成搜索,即所有备选站点都选择了相应的车辆数,计算每只蚂蚁对应的方案所产生的社会总成本,并且保留m只蚂蚁中成本最小的解。同时,更新(i,j)上的信息素。首先是信息素挥发,其次是蚂蚁在它们所经过的边(i,j)上释放信息素。信息素更新公式如下:μij=(1-ρ)μij,式中,ρ表示信息素挥发系数(0<ρ≤1)。 式中,Ck表示蚂蚁k的车辆布局方案所对应的EMS总成本。明显地,EMS的成本越低,相应的(i,j)边上获得的信息素越多,则在以后的迭代中更有可能被其他的蚂蚁选择,形成一个正反馈机制。 m只蚂蚁遍历所有站点完成一次循环后,保留本次迭代中m只蚂蚁中成本最小的解,清空禁忌表,重新回到初始站点,准备下一次迭代直到完成事先设定的迭代次数。算法流程如表2所示。 表2 改进蚁群算法流程 多时段的解是在每个时段不同的行驶速度、救护车可获得率以及需求的数量及分布下的救护车的布局方案。在上述的蚁群算法的基础上再嵌套一层时段t的循环,对于每一时段t,都重新初始化该时段对应的行驶速度,需求数量和空间分布以及救护车不可获得率,分别求得时段t的最优布局方案,完成所有时段迭代后,计算所有时段的EMS社会总成本。 根据收集的上海市松江区2014年的急救数据,进行实证分析。松江区位于上海市西南部,总面积约605.64平方千米。首先,利用“网格法”将松江区划分为144个需求点,每个需求点为2.5km×2.5km的单位网格。其次,对从上海市松江区120急救中心系统中导出的救护车数据进行初步筛选和清理,去除非急救出车等无效数据,得到2014年的松江区的总的急救需求数量为25941(分布如图1所示)。再次,为了详细刻画一天中各时段需求量的变化、需求空间分布的变化以及行驶速度的变化,本文将一天均等划为24个时段,每个时段时长1小时。按照划分的时段将总需求量归类,得到每个时段的需求量情况(如图2所示)。最后,根据不同时段的每个具体需求位置的经纬度,将需求集合到划分的单位网格中,得到每个时段需求的空间分布。因上海路网呈南北-东西走向,所以根据站点和需求点的经纬度,计算需求点和站点之间的直角边距离,近似估算两者之间的实际距离。 图1 2014年上海市松江区急救需求与站点分布 实证中不同时段的行驶速度数据来源于上海市交通出行网,全时段的平均行驶速度为46.56km/h,其中早高峰7∶00到9∶00期间的平均行驶速度约为41.67km/h,晚高峰17∶00到19∶00的平均行驶速度为37.93km/h,具体情况如图2所示。 图2 各时段需求量与行驶速度 根据实地调研结果,对EMS社会总成本进行估算。平均每个急救站点的建设成本约150万元,土地租金每年约10万元,租期长为30年,据此折算每个急救站点的平均年运营成本Cst=150万元/30+10万元=15万元。救护车的运营成本包括救护车的使用费用以及随车人员的工资,其中车辆购置费用约为40万元/辆(包括车载医疗设备费用),平均使用年限为10年。每辆救护车配备5名工作人员,年薪约6元万/人。此外救护车的维护费用以及油费每年约6万元。因此救护车每年平均运营成本Cam=40万元/10+6万元×5+6万元=40万元。根据Su等[13]的研究,院前急救中普通病患呼叫比例为7.662%,严重病患呼叫比例为92.338%。通过查阅相关因急救延误造成的司法案件,根据案件中的诉讼赔偿金进行估算,严重病情的急救延误损失成本为5000元/分钟,普通病情的急救延误损失成本为500元/分钟。 根据2014年上海市松江区急救数据统计,松江区现有8个救护车站点,26辆救护车。设定每个站点车辆最大容量为3。由于目前中国没有法律规定的急救覆盖标准,因此根据《美国医疗急救服务法》中的规定,设置r1(α)为10分钟(80%),r2为20分钟。 利用第四部分设计的启发式算法求解模型,在保证所有需求点在低标准时间r2内被覆盖,80%的需求在高标准时间r1内被覆盖的条件下,寻求使EMS的社会总成本最小化的车辆布局方案。求解结果如表3所示。总成本指在各个时段上EMS一年的社会总成本,包括延误成本和运营成本两个部分。双覆盖率指被高标准r1覆盖两次及其以上的比例,即能被救护车在10分钟内多次响应的需求比例。单覆盖率指被高标准r1覆盖一次的比例,车辆数指每个时段的救护车布局方案中所有站点停放的车辆总数。繁忙率根据Soo-Haeng[5]提出的实际繁忙率计算方法,通过总需求、车辆数和平均出车时间进行估算(需求*平均出车时间/车辆数),用以衡量救护车的闲忙程度。根据结果,可以发现EMS的社会总成本在9∶00~10∶00以及19∶00时达到峰值,这是由于在这两个时间点,急救需求的数量较大,并且位于早晚高峰时期行驶速度较慢,所以导致难以及时响应需求,延误成本增加。这两个时段救护车的繁忙率大约处于0.2到0.3左右,工作负荷量并不大,因此即使再增加救护车数量只会导致运营成本的增加速度大于延误成本的减少速度从而使总成本增加。而在0∶00~7∶00时段,急救需求较少且行驶速度较快,因此未能及时响应导致的延误成本小,救护车布局数量相应减少使运营成本较小,从而使EMS的总成本较小。此外,根据结果可以得到急救网络的平均双覆盖率达到75.71%,平均一次覆盖率达到88.75%高于设定的80%的服务水平。各个时段的繁忙率比较平均,位于0.2~0.3之间,可见根据需求和行驶速度随时间的变化,调整车辆规模可以平衡各时段救护车的工作负荷。 表3 模型结果 根据表4,优化后的系统总成本比原系统下降了32.23%,虽然从表面上看原系统的双覆盖率高于优化后的系统,但两者的延误成本基本持平,说明原系统过高保证了双覆盖率,造成救护资源的浪费和冗余,优化后的系统在保证院前急救服务水平和急救效果的情况下减少了车辆资源,提高了EMS的效率。 表4 原系统与优化系统对比 上文中根据每小时需求和速度的变化得到的布局方案,再布局调整太过频繁,在实际中难以应用。考虑到急救服务系统管理的便捷性和调度的可操作性,本节将对得到的车辆布局方案进行分析,确定合适的再布局时间点以及调度方案,从而即方便EMS网络的管理又有效地降低EMS社会总成本,提高效率。 根据急救调度中心的实际情况,一天24小时内安排3个调度班次,每班工作时长8小时。通过计算各个时段的布局方案之间的欧式距离刻画方案间的差异性,布局方案的差异越小则再调度调整越少,时段间的需求规模、分布和行驶速度也越相近,则更适合整合成同一调度班次。根据实际排排班要求和布局方案差异的分析,确定时段8、16以及24分别为再布局时间点,一天被均匀地划分为8小时的三个调度班次。再根据重新划分的时段的需求和行驶速度,得到新的调度方案(如表5所示)。新的调度方案中,第二和第三个调度班次布局相同,因此实际中只用在7点时进行重新布局调度。基于新划分的时段的需求和速度数据,分别根据各时段优化后的调度方案和原系统的车辆布局方案计算EMS总成本,原系统和优化后的结果如表6所示。优化后的系统总成本比原系统下降了29.03%,虽然从表面上看原系统的多次覆盖率高于优化后的系统,但两者的延误成本相差较小,说明原系统过高保证了多次覆盖率,造成救护资源的浪费和冗余,优化后的系统在保证院前急救服务水平的情况下减少了车辆资源,提高了EMS的效率。 表5 车辆布局方案 表6 原系统与新的优化系统对比 为了说明考虑需求和行驶速度随时间变化的重要性,下文将对多时段模型和静态模型进行对比。利用蚁群算法求解静态的模型,基于平均行驶速度和各时段总需求量及分布的数据,得到车辆布局方案,再将该方案带入各时段实际环境中,计算EMS社会总成本及相关结果。静态模型和多时段模型在各个时段的成本及覆盖率对比如图3所示。除了在时段8和23总成本持平外,其他时段中多时段模型的总成本明显低于静态模型的总成本。多时段模型的双覆盖率在24和时段1到7低于静态模型的双覆盖率,而在其他时段均高于。从整体上来看(见表7),静态模型的年总成本约为1500万元,而多时段模型的年总成本为1263万元,考虑需求和速度随时间的变化使EMS的成本下降了15.8%。静态模型的双覆盖率为62.87%,多时段模型的双覆盖率为75.71%,提升了12.84%。此外,静态模型的繁忙率的方差为0.011561,而多时段模型的0.000962,下降了91.68%,说明静态模型中救护车的工作负荷不均衡,而多时段模型显著平衡了车辆的工作负荷。 图3 多时段模型与静态模型各时段对比 上文中的实例分析应用了第四章中设计的启发式算法求解。为了验证改进后算法的有效性,本节将分别利用设计的启发式算法、改进前蚁群算法以及CPLEX对多个规模的样本进行求解。在4、8、23个站点的情境下求解,对比结果如表8所示。 对于4个站点的情况,CPLEX给出了精确解。然而CPLEX在10小时内得出的优化结果仅比改进的算法在5分钟得到的结果高0.23%。对于8个站点和23个站点的情况,CPLEX在10小时内未找到最优解。 本文设计的算法是将蚁群算法结合贪婪算法的思想,针对多时段模型的特点,分阶段对解进行编码(详见第四章),而改进前的蚁群算法指直接利用蚁群算法对多时段模型进行编码。三种站点规模的测试中,改进前后算法参数设置一致:蚂蚁数m=50,迭代次数N=100,信息挥发系数为p=0.15,α=0.1,β=2.5。结果表明虽然改进后的蚁群+贪婪算法运算时间较改进前蚁群算法的时间长,但在可接受范围内,并且改进后算法的优化结果分别比改进前高出5.16%、9.77%和18.48%,提高了求解结果的精确度。 表8 算法分析对比 本文提出了多时段的成本效益DSM模型,考虑了需求数量、需求空间分布、行驶速度以及救护车不可获得率等因素随时间的变化。在保证一定服务水平的条件下,最小化所有时段社会总成本。模型根据需求规模变化配置相应车辆规模,以平衡各时段工作负荷。根据需求空间分布、行驶速度和救护车不可获得率变化动态调整救护车布局方案,从而保证急救服务水平,降低EMS社会总成本。 利用上海市松江区2014年的急救数据,本文进行了实证分析。优化后的系统在保证80%的高标准覆盖水平下,社会总成本比原系统下降了32.23%。优化后的系统与原系统的延误成本基本持平,说明两者的急救服务效果相同,而优化后的系统减少了急救资源数量,因此降低了社会总成本。为了使布局方案在实际运营中具有可操作性,避免每小时频繁的调动与再布局,本文分析各时段布局方案的差异性,将一天划分为三个时段,每时段时长8小时,确定再布局时间点为7∶00,并得到相应布局方案。与原系统相比,重新制定的布局方案使系统的社会总成本下降了29.03%。 通过多时段模型与静态模型的对比,验证了考虑随时间变化的不确定性因素的重要性。由于多时段中考虑了需求、行驶速度及救护车不可获得率随时间的变化,多时段模型的EMS的总成本比静态模型的总成本下降了15.8%,并且双覆盖率提高了12.84%。此外,相比静态模型,多时段模型显著降低了各时段救护车繁忙率的方差,有效平衡了车辆工作负荷。 本文针对多时段模型的特点,基于蚁群算法和贪婪算法思想,提出了一种改进的启发式算法。在不同站点规模下的测试结果表明,相比CPLEX和原始的蚁群算法该算法在运行速度和精确度上表现良好。 本文的研究虽然在动态环境中研究EMS布局问题,但由于数据收集的限制,没有考虑行驶速度在各时段空间分布上的变化,即只考虑行驶速度在各时段上的平均速度。根据Schmid[16]的研究,考虑行驶速度在空间上的不确定性可使覆盖范围提高10%。此外,本文的模型是单阶段的,即只考虑了救护车到急救病人的过程,而没有考虑将病患送往医院的过程。Soo-Haeng[5], Liu和Yang[6]的研究均表明考虑两阶段对救护车布局问题的重要性,以后的研究中,可进一步分析。2 问题描述与建模

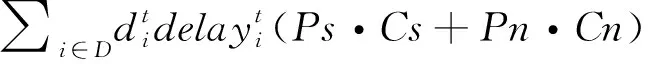
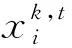
3 算法设计
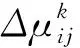

4 实证分析
4.1 数据描述
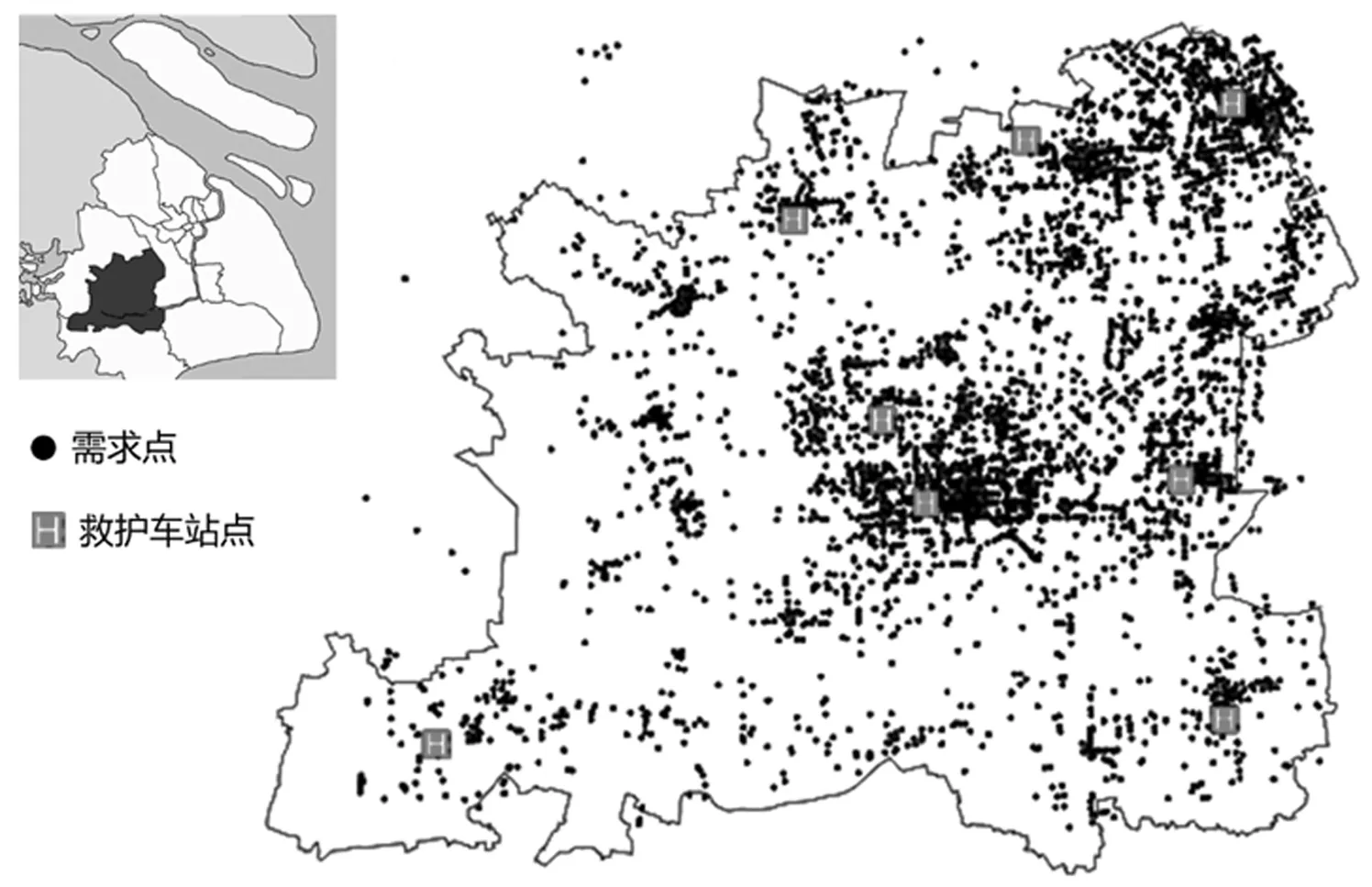
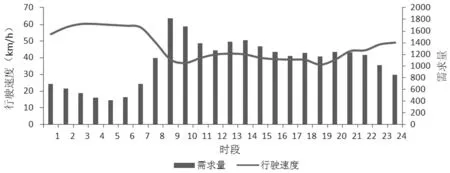
4.2 结果分析
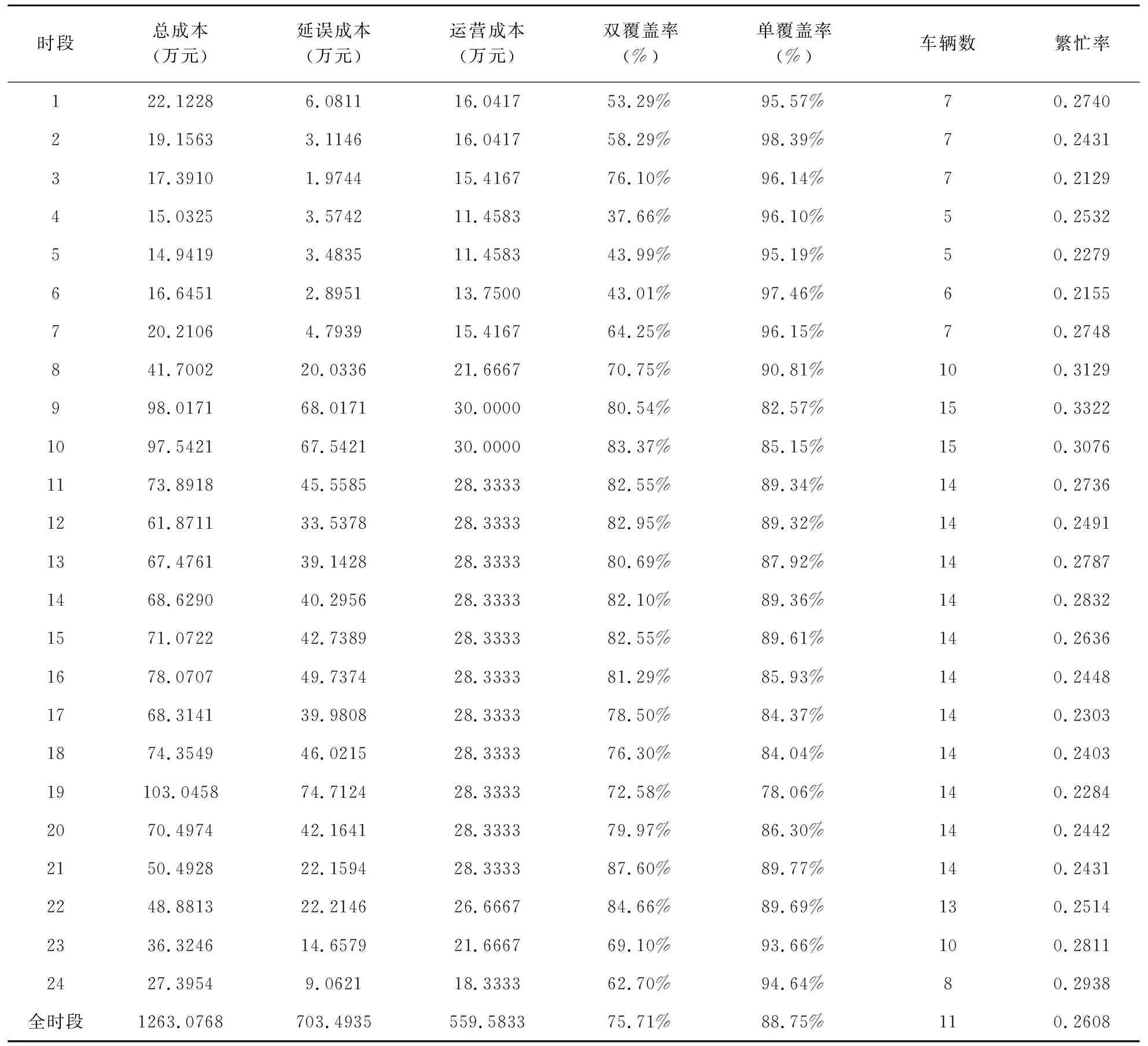
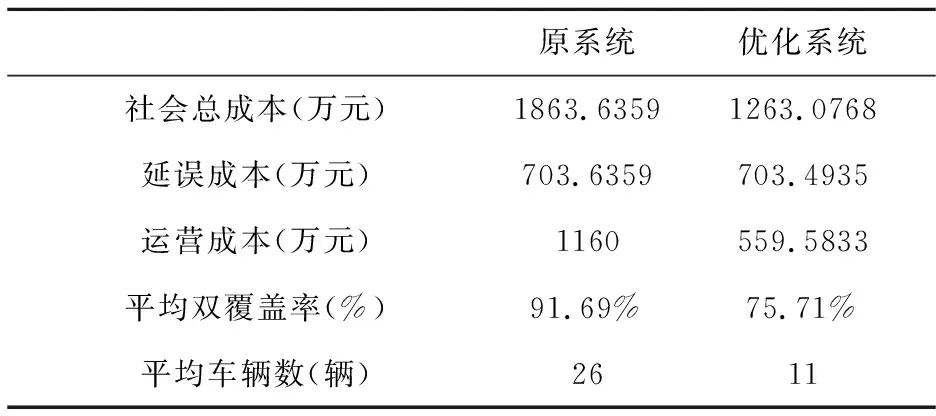
4.3 实际应用分析
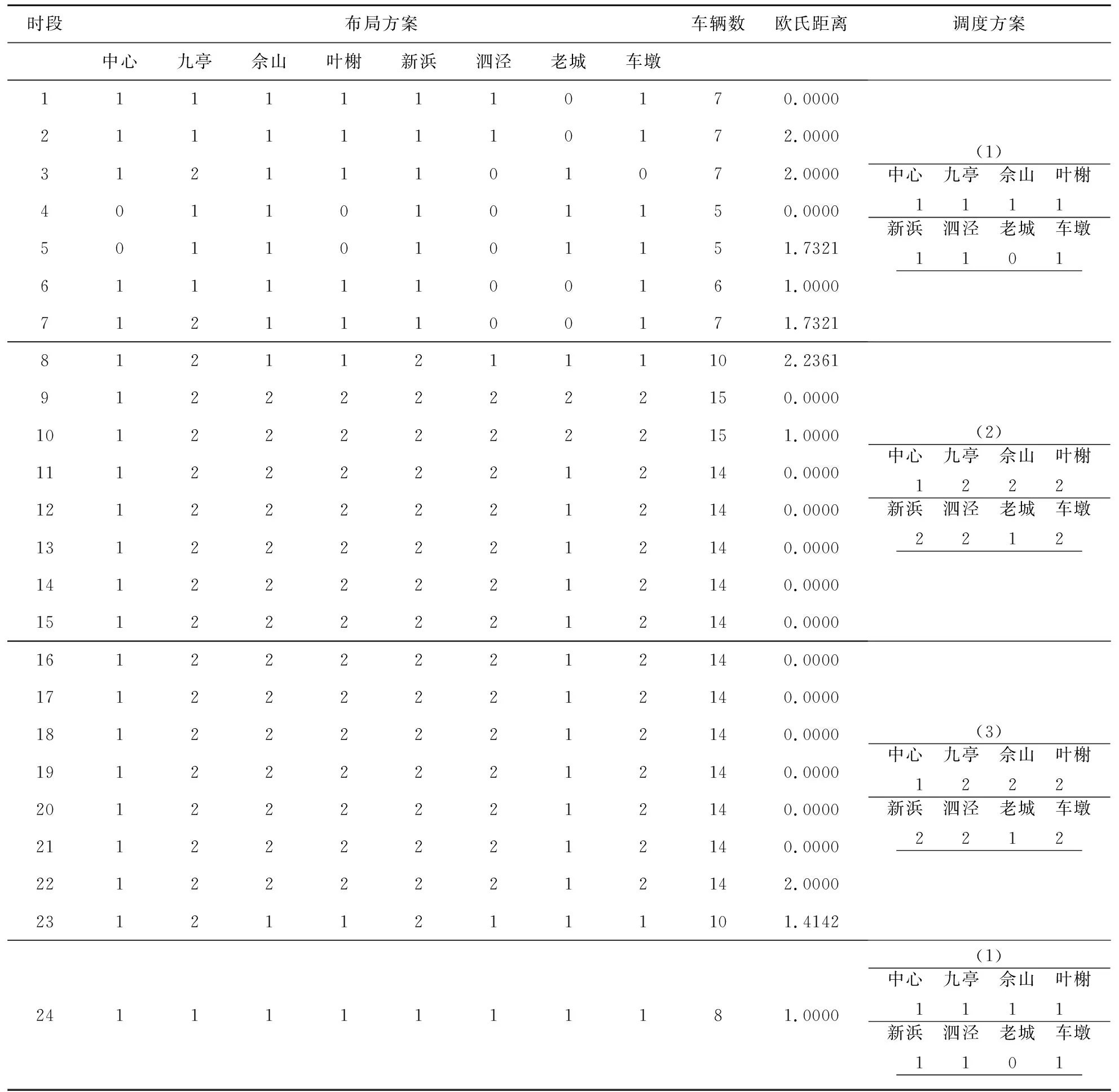
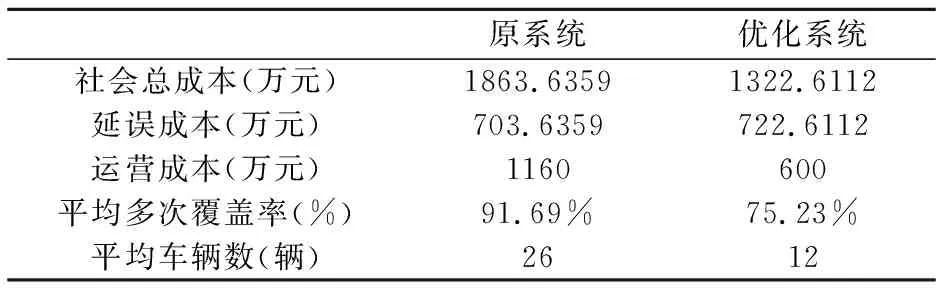
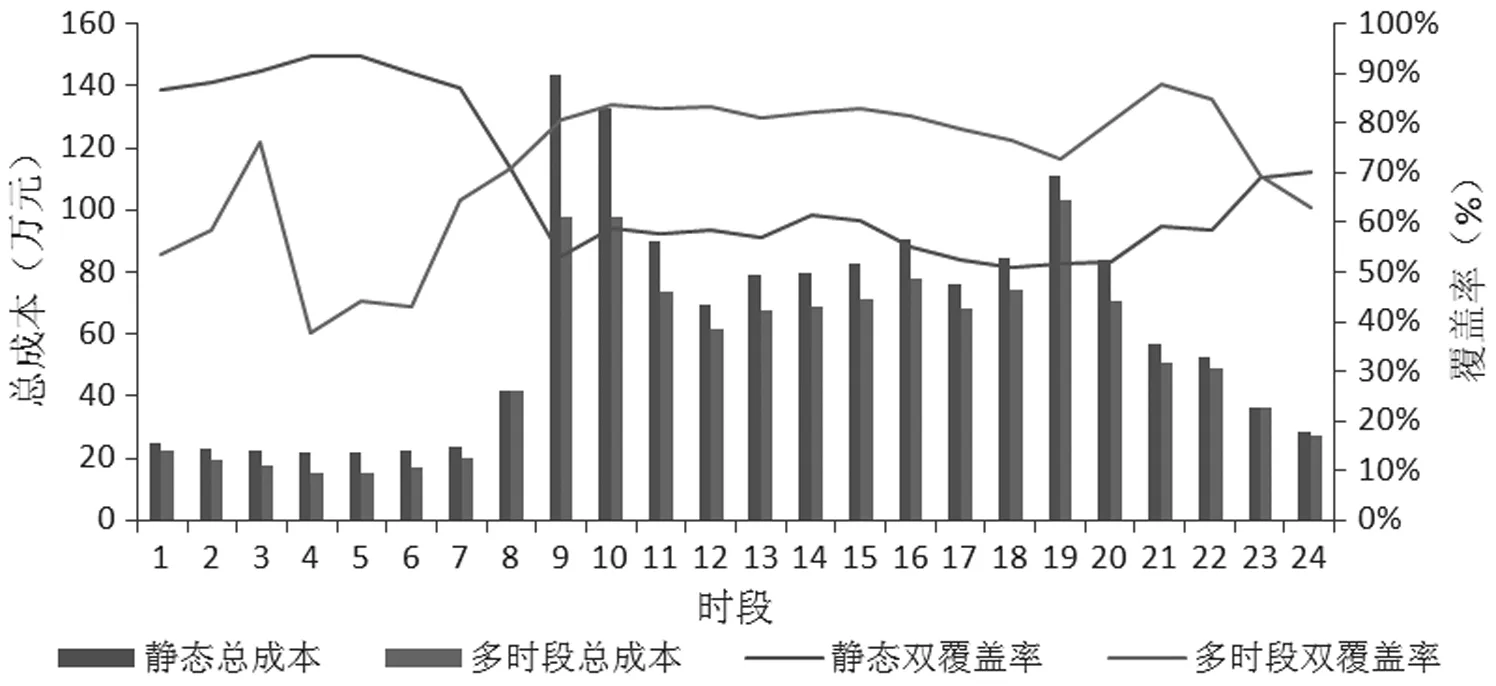
4.4 多时段模型与静态模型对比
4.5 算法分析

5 结论

