政府奖惩下供应链合作减排与低碳宣传的动态优化

王道平, 王婷婷

(北京科技大学 东凌经济管理学院,北京 100083)

0 引言

随着全球人口的递增以及经济规模的扩大，能源使用引发的环境问题，如全球气候变暖和极端气候频繁出现，严重影响了人类的生活。各国已形成共识：人类在生产和生活中排放的CO2是导致温室效应和极端气候频繁产生的主要根源。面对如此严重环境问题，亟需改变和提升现有技术以及社会行为模式。2015年1月，我国正式实施新修订的《中华人民共和国环境保护法》，开启了我国环境治理的新篇章。2017年，北京市电镀、铸造、建材、化工以及印刷等500家以上污染企业被关停退出；江西宜春中安公司等5家企业被判赔偿环境修复费用3700余万元。这表明，可持续发展是企业获取持续竞争力的重要因素。

通过大量的研究发现，生态技术创新企业通过提高自身的生态效率及塑造低碳形象，能够获得比竞争对手更多的市场优势。随着人们的低碳环保理念逐渐加深，消费者越来越青睐于节能减排产品。因此，可通过制造商的低碳研发投入实现节能减排产品的生产，与此同时，零售商可通过低碳宣传推广提升消费者的低碳偏好意识，进而扩大市场需求，间接激励制造商进行低碳生产。为进一步降低产品生产过程中的碳排放，政府也可以通过奖惩措施积极参与碳减排，激励企业进行低碳生产。因此，在考虑政府奖惩机制下，对供应链合作减排与低碳宣传问题的研究具有重要的理论及现实意义。

1 文献综述

低碳背景下，企业的减排决策已成为学术界的热点话题，且已有很多学者从企业运营的角度进行了相关的研究。Sarkar等考虑企业在运输产品时控制碳排放的情况下，建立三阶段供应链模型，以降低供应链成本[1]。Aljazzar在综合考虑延迟付款、运输成本以及碳排放成本下，研究买方在收到物品后延迟付款的各种情形，研究表明采用延迟付款可以改善供应链的环境和经济绩效[2]。付秋芳等考虑供应商和制造商组成的二级供应链，研究供应链成员的碳减排投入行为和策略，研究发现供应链参与成员的碳减排投入策略和两者碳减排收益比紧密相关[3]。周艳菊等以制造商和零售商组成的供应链为对象，研究了零售商考虑公平关切前后，所设计的两种契约对供应链最优决策以及渠道协调的影响情况[4]。李友东等在低碳背景下对比分析了两种成本分摊契约下碳减排、定价以及供应链成员收益，研究表明这两种契约下都实现了零售商和制造商一起降低碳排放的目标[5]。Yang等考虑了由制造商和零售商构成的两条竞争性的供应链，对比分析供应链纵向合作和横向合作，并引入了收益共享契约，不仅实现了供应链成员间的共赢，还提高了减排率[6]。Li等以单个制造商和具有竞争关系的两个零售商组成的闭环供应链为研究对象，研究了供应链纵向合作减排、横向合作减排以及低碳宣传的最优决策行为[7]。

此外，节能减排是与政府和企业密切相关的社会性问题，政府有必要以引导者的身份对企业实施监管。近些年，已有部分研究者关于政府奖惩政策进行了深入地研究。Ferrer等在奖惩机制下，对存在制造商竞争的闭环供应链的决策问题进行了研究[8]。王文宾等以闭环供应链为研究对象，对基于回收率以及回收量的奖惩机制下的决策进行了对比，发现基于回收率的奖惩机制对闭环供应链回收率的提高具有更好的引导作用[9]。Wang等研究了制造商和回收商之间收集废弃电子电器设备的责任分配问题，且政府通过奖惩机制激励企业的回收努力水平[10]。易余胤等采用博弈论构建了两种回收契约模型，从回收率、零售价以及利润等方面对这两种契约进行了对比，得到了制造商对回收契约进行选择的临界值；并在考虑政府奖惩时改进了总费用奖惩契约模型[11]。焦建玲等在奖惩机制下，研究碳排放约束下的演化博弈，探讨碳交易价格、碳配额以及政府监督成本等参数对演化稳定策略的影响情况[12]。

上述文献主要是通过静态模型进行研究，然而考虑到企业经营往往会跨越多个周期，因此有必要对低碳供应链长期动态合作减排问题进行研究。Mohamad通过建立两阶段动态协调模型，考虑对超出碳排放限值而进行惩罚时，供应链管理者如何选择最佳合作模式[13]。Liu等构建了随机微分博弈合作模型，研究不确定条件下供应链的最优动态协调策略，且为使系统利润最大化，分析如何协调供应链成员的努力水平[14]。叶同等以供应商和制造商组成的供应链为研究对象，在考虑消费者低碳偏好以及参考低碳水平因素下，运用微分博弈研究供应链联合减排的协调问题[15]。黄宗盛等借助微分对策理论，研究在考虑具有竞争性零售商下，制造商和零售商构成的闭环供应链的最优控制策略[16]。Jørgensen等通过构建三个企业间进行广告竞争的微分博弈模型，确定各参与者的联盟价值函数，并分析这些企业之间的合作契约能否长久持续[17]。徐春秋等通过构建供应链联合减排与低碳宣传的三种微分博弈模型，发现一定条件下，设计的契约实现了供应链成员及系统总利润的Pareto改善，为供应链上下游企业制定合理的合作策略提供一定的参考[18]。赵道致等引入竞争因素，借助微分博弈方法，进一步研究供应链上下游联合减排与低碳宣传的问题[19]。周熙登通过构建双渠道供应链微分博弈模型，研究低碳宣传、减排以及品牌策略问题，发现低碳宣传策略和品牌差异程度以及不同渠道下供应链成员的边际利润相对大小均相关[20]。游达明等将价格因素考虑在内，建立微分博弈模型，研究供应链低碳研发和促销问题，并对不同决策下低碳供应链的均衡策略进行了比较分析[21]。

基于对现有文献的回顾和梳理，可知低碳供应链运营问题已经是国内外学者研究的热点之一，而且从动态角度研究低碳供应链运营以及关于政府奖惩行为的研究已经取得一些研究成果。但是鲜有文献从动态的角度将政府奖惩、合作减排以及低碳宣传等因素同时引入到低碳供应链决策中进行研究。再者，由于作为影响需求的关键因素之一的产品碳排放量随着时间的推移，存在自然增长的状况。鉴于已有成果及上述分析，本文构建了分散式和集中式微分博弈模型，并通过算例对两种决策情形进行仿真分析。

2 模型建立与求解

2.1 模型的假设与符号说明

本文借助微分博弈理论，研究由制造商M和零售商R组成的供应链系统长期合作减排与低碳宣传的问题。其中，制造商负责生产产品，进而通过零售商销售产品，零售商的低碳宣传直接影响低碳产品的市场需求。

主要符号说明见表1。

表1 模型参数说明

文中主要提出如下假设：

假设1考虑到减排成本和低碳宣传成本均为各自努力水平的凸函数，则t时刻制造商的减排成本为：

(1)

其中，ηM为制造商的减排成本系数；t时刻零售商的低碳宣传成本为：

(2)

其中，ηR为零售商的低碳宣传成本系数。

假设2借鉴文献[22]关于环境污染动态模型的思想，制造商投入减排努力可更新设备、改进生产流程等，进而生产出的单位产品碳排放量会降低，因此产品碳排放量受当期制造商减排努力水平的负向影响，那么产品碳排放量的微分方程可表示为：

(3)

其中，x(t)和x0分别为t时刻和初始时刻产品碳排放量；ω(ω>0)为当制造商减排努力水平为零时，碳排放量的自然增长率；这里假定由于随着时间的推移，已投入的减排设备不断老化等原因，碳排放量存在自然增长的趋势；ε(ε>0)为制造商减排努力水平对碳排放量的影响系数。当制造商生产过程中碳排放量x(t)小于L时，政府给予制造商k(L-x(t))的奖励，否则，当碳排放量x(t)大于L时，则给予k(x(t)-L)的惩罚。

假设3本文为了研究问题的方便，主要考虑制造商和零售商受减排、低碳宣传的影响，不考虑制造商和零售商的库存和缺货成本，不考虑需求受价格等因素的影响，且二者决策基于完全信息；即产品需求受产品碳排放量和低碳宣传努力水平的影响[23]，所以产品需求可表示为：

D(t)=D0+αER(t)+β(x0-x(t))

(4)

其中，D0(D0≥0)为产品的初始需求，α(α>0)和β(β>0)分别为低碳宣传努力水平和碳排放量对需求的影响系数。

假设4制造商和零售商在无限时间范围内的任何时刻贴现因子ρ(ρ>0)均相同，且制造商和零售商的边际利润ΠM和ΠR均为常数。

综上所述，制造商、零售商和供应链的长期利润分别为：

(5)

(6)

CR(ER(t))-k(x(t)-L)]dt

(7)

为方便书写，下文省略t。

2.2 供应链减排与低碳宣传模型

1)分散式决策

本节研究零售商充当合作减排的领导者，而制造商充当跟随者的角色，双方积极进行合作减排。制造商通过改进生产技术进行减排，而零售商通过低碳宣传增大低碳产品的市场需求。为提高制造商的减排积极性，除采用政府奖惩措施外，零售商为制造商分担θ(0≤θ≤1) 比例的减排成本。那么，制造商和零售商的决策目标分别为:

(8)

(9)

命题1分散式决策均衡结果：

(1)零售商为制造商分担的减排成本比例、制造商的最优减排努力以及零售商的最优低碳宣传努力分别为：

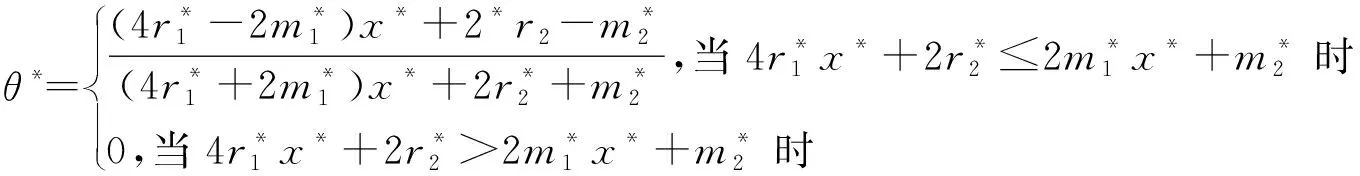
(10)

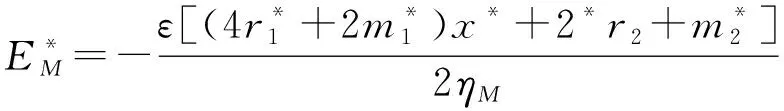
(11)

(12)

(2)产品碳排放量的最优轨迹：

(13)

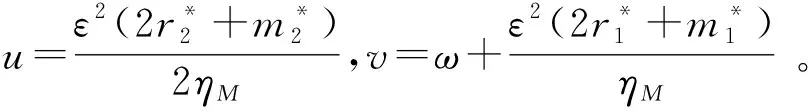
(3)产品需求量：

(14)

(4)制造商、零售商和供应链的最优利润值分别为：

(15)

((16)

(17)

其中

推论1分散式决策下，产品碳排放量的最优轨迹随着时间的变化，呈现出的变化趋势受参数u和v的影响，具体趋势见表2。

表2 分散式决策下产品碳排放量随着时间的变化情况

由推论1可知：(1)当参数符合情况1时，随着时间的推移，产品碳排放量的最优轨迹逐渐减小且收敛于某一水平，说明供应链长期合作减排效果随着时间的增加而增大，且具有边际递减效果；即随着制造商不断进行减排投入，企业减排效果逐渐减弱，这种情况比较符合实践。(2)当参数符合情况2时，产品碳排放量随着时间递减且趋向于负无穷，说明供应链长期合作减排效果随时间的增大而增大，且具有边际递增效果，即企业的长期减排效果增幅很明显。(3)当参数符合情况3和4时，随着时间的推移，产品碳排放量的最优轨迹逐渐递增，长期下去会对环境带来不良影响；在这两种情况下，政府应出台相应的规章制度，引导企业重新做出合理的减排决策。

2)集中式决策

集中式决策(用上标c表示)下，双方以供应链总利润最优为目标，则此决策下的决策目标为：

(18)

命题2集中式决策均衡结果：

(1)制造商的最优减排努力和零售商的最优低碳宣传努力分别为：

(19)

(20)

(2)产品碳排放量的最优轨迹：

xc*=(x0+λc)e(ρ-ω)t-λc

(21)

(3)产品需求量：

(22)

(4)供应链的最优利润值为:

(23)

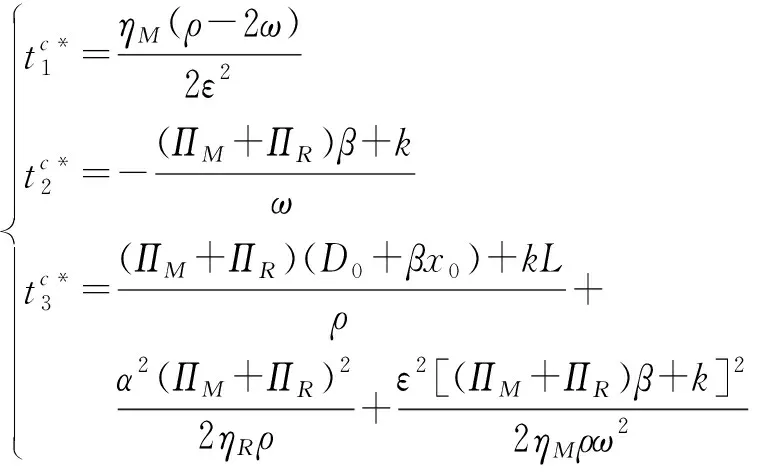
推论2集中式决策下，产品碳排放量的最优轨迹随着时间的变化，呈现出的变化趋势受参数ρ、ω、λc以及x0的影响，具体趋势见表3。

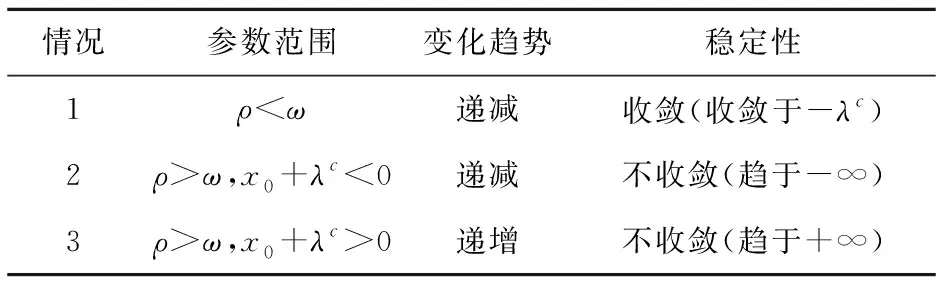
表3 集中式决策下产品碳排放量随着时间的变化情况

由推论2可知：(1)推论2中情况1的收敛性类似于推论1中情况1的收敛性，而推论2中情况2和3分别与推论1中的情况2和4具有相似的敛散性，具有相似的管理意义。

由命题1、2以及推论1、2可得推论3和4。

推论3的证明省略(直接相减与零比较，进而确定大小关系)。推论3说明了当分散式和集中式两种决策情形下，产品碳排放量的最优轨迹均收敛于某一水平时，集中式决策下低碳宣传努力水平、产品需求以及供应链总利润均高于分散式决策下的对应值，而产品碳排放量具有相反的情况；即与分散式决策相比，在集中式决策下上下游企业间合作减排能够使供应链总利润增加，且兼顾环境，实现了共赢。

然而值得注意的是虽然集中式决策下制造商和零售商的合作减排能使得供应链总利润实现最大化，但是若要使二者自愿进行合作减排，还需要满足约束条件；即制造商和零售商在集中式决策下各自分得的利润大于分散式决策下各自分得的利润，对应的约束条件为：

(24)

(25)

并且集中式决策下制造商和零售商各自利润的增量占供应链系统总利润增量的比例取决于双方的谈判能力以及渠道能力。

推论4集中式决策情形下，当ρ<ω时，产品碳排放量与政府的奖惩力度呈负相关，产品需求量与政府奖惩力度呈正相关。

证明集中式决策下，求式(21)关于k的一阶偏导可得

因为ρ<ω，所以∂xc*/∂k<0，因此集中式决策情形下，当ρ<ω时，产品碳排放量与政府的奖惩力度呈负相关。同理可证∂Dc*/∂k>0，即集中式决策情形下，当ρ<ω时，产品需求量与政府奖惩力度呈正相关。

3 算例分析

本文将借助MATLAB分别对分散式和集中式这两种博弈情形做算例分析。给定各参数值分别为：MM=900，MR=700，ηM=20，ηR=15，ω=2，ε=0.4，α=0.6，β=0.3，ρ=0.9，D0=15，x0=12，k=2，L=1，t=1。

表4比较了分散式和集中式这两种决策下的博弈均衡结果。

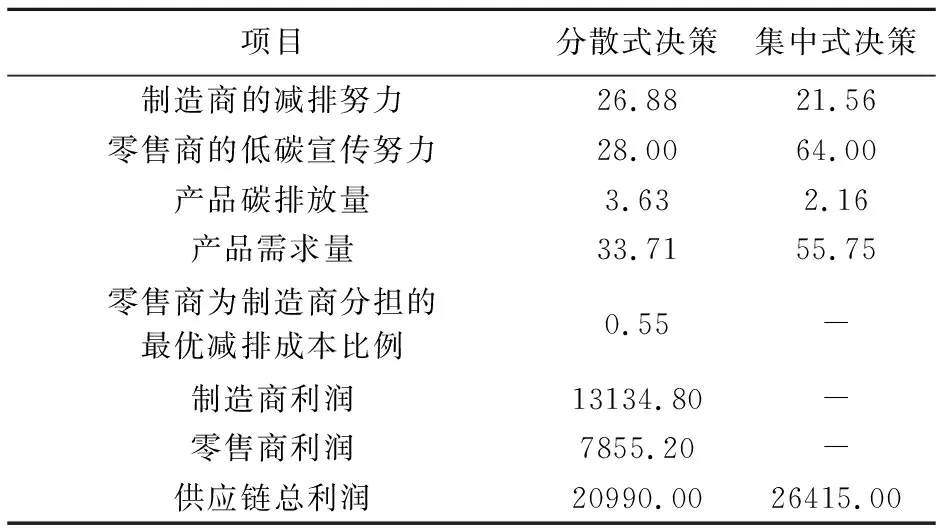
表4 不同决策下博弈均衡结果

由表4可知：相比于分散式决策，集中式决策下零售商的低碳宣传努力提高了128.6%，产品需求量提高了65.4%，产品碳排放量降低了40.5%，供应链总利润提高了25.8%，说明集中式决策下供应链总利润实现了Pareto最优，且兼顾了环境。然而分散式决策下制造商的减排努力水平高于集中式决策下对应的值，这是由于分散式决策下，零售商为制造商分担了一部分减排成本，对其具有较强的激励作用而引起的。

鉴于篇幅有限，本文只对部分参数进行了仿真分析。在分散式和集中式决策下，产品碳排放量以及制造商和零售商的努力水平随时间的变化情况如图1和2所示。

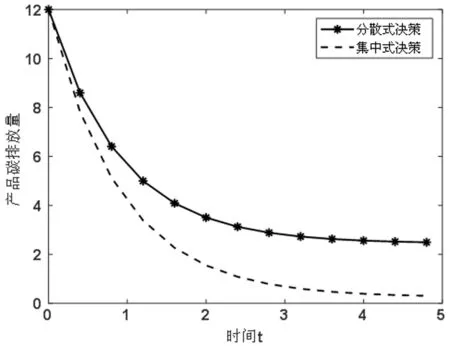
图1 产品碳排放量随时间的变化情况

由图1可知，在分散式和集中式两种决策下，产品碳排放量均随着时间的增加而不断减小且逐渐趋于稳定，即产品碳排放量的减小速率越来越小，表明此系统的合作减排与低碳宣传过程为可控的。由图2可知，在分散式和集中式两种决策下，制造商的减排努力均随着时间的增加而减小并逐渐趋于稳定，即随着减排效果边际递减，制造商投入的减排努力也相应的减少，符合实际情况；零售商的低碳宣传努力均为恒定值。同一时刻，集中式决策下供应链参与成员的努力总和高于分散式决策下双方努力之和，说明集中式决策下，供应链参与成员付出的总努力程度较大；初始时刻制造商的减排努力水平在集中式决策下比在分散式决策下高，但随着时间的推移出现了相反的情况，这是由于零售商为制造商分担了一部分减排成本，提高了制造商减排的积极性。

图3～6分别为在分散式和集中式决策下参数ε、ηM、β以及k对产品碳排放量的影响。

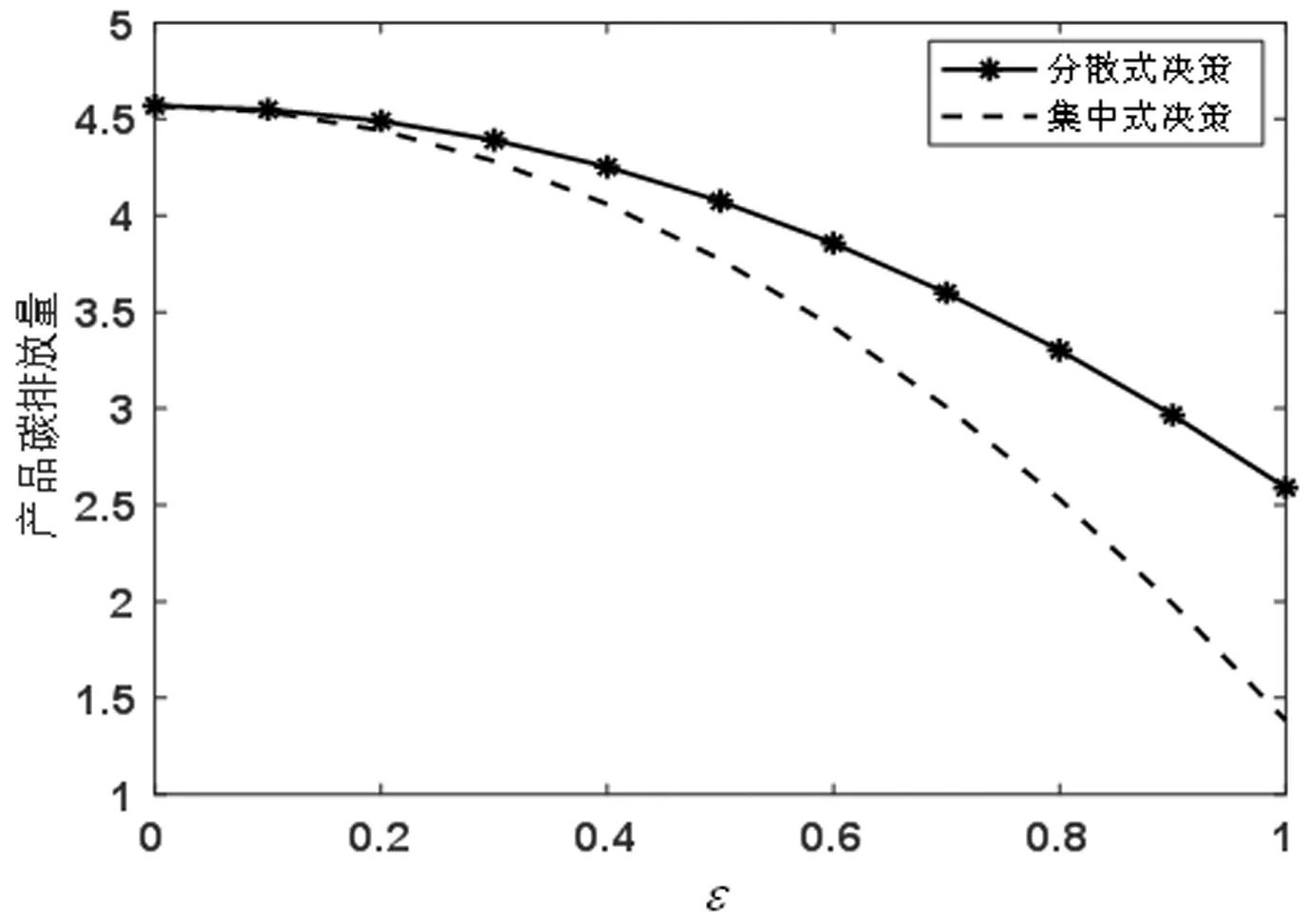
图3 参数ε对产品碳排放量的影响

从图3可知，同一时刻，在分散式和集中式决策下，产品碳排放量均随着产品碳排放量对制造商减排努力敏感系数ε的增大而减小，且减小的速度越来越大，表明随着制造商减排努力转化为产品减排量难度的增大，供应链合作减排效果越差。集中式决策下产品碳排放量较分散式决策时得到降低，且相比于分散式决策时，集中式决策下产品碳排放量的降低值随着参数ε的增大而增大，表明制造商减排努力对碳排放量的影响系数越大，供应链的减排效果在集中式决策时的优势越显著。从图4可知，同一时刻，在分散式和集中式决策下，产品碳排放量均随着制造商减排成本系数ηM的递增呈上升趋势，说明供应链长期合作减排的正面效果随着单位减排成本投入的增大而增强。

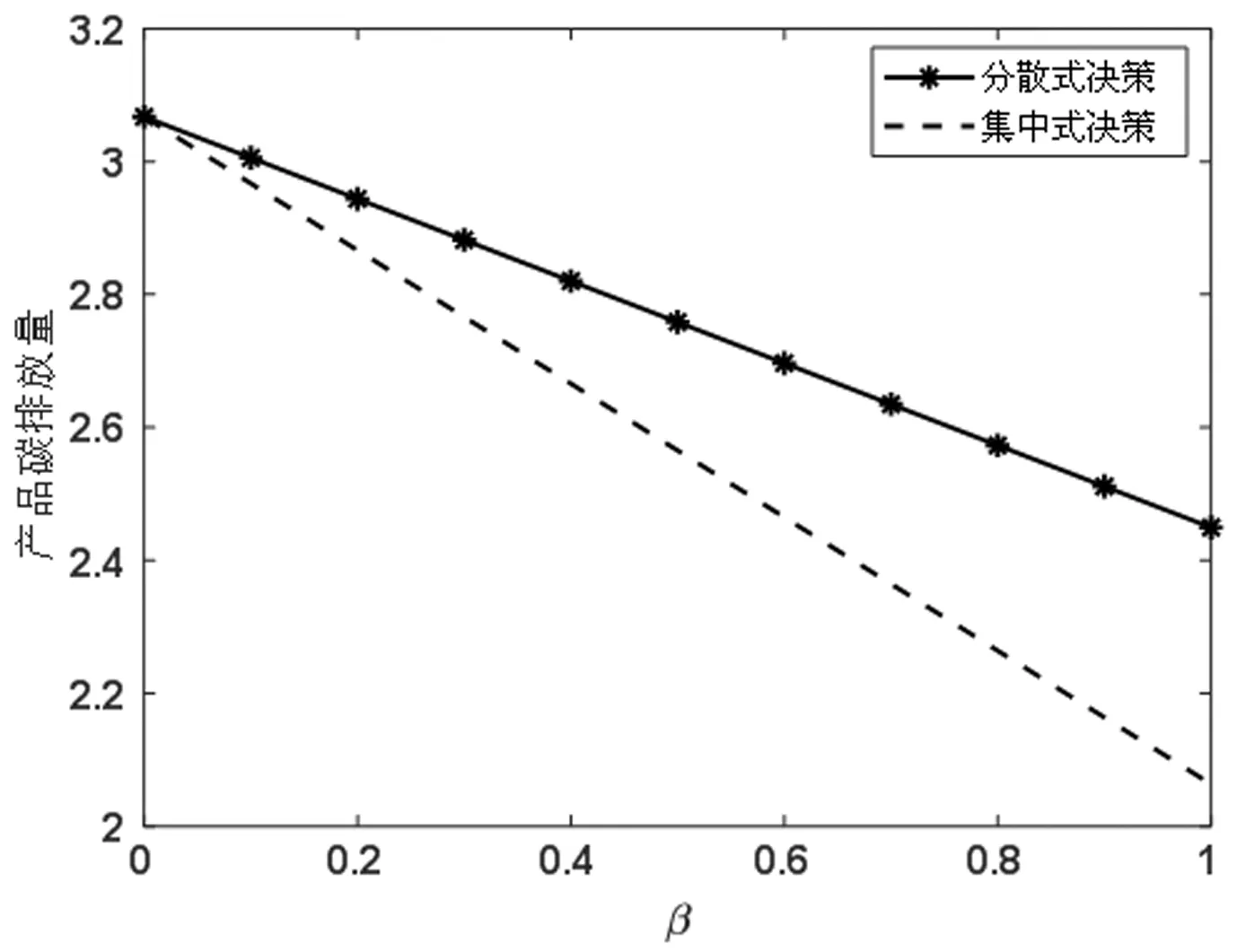
图5 参数β对产品碳排放量的影响

由图5可知，在同一时刻，对分散式和集中式决策而言，产品碳排放量对需求的影响系数β越大，产品碳排放量越小，说明消费者购买低碳产品的意愿越强，产品碳排放量越低；且与分散式决策时相比，集中式决策时产品碳排放量的降低值随着碳排放量对需求的影响系数的增大而增大，表明消费者低碳意识越强，集中式决策下供应链长期合作减排的优势越显著。由图6可知，在集中式决策下，产品碳排放量随着政府奖惩力度k的增大而减小，说明政府可通过增大奖惩力度，提高供应链成员合作减排的效果。

集中式决策下，政府奖惩力度k以及其他参数ω和t对产品碳排放量的影响情况，如图7和8所示。

图7 参数k随着时间t的变化对产品碳排放量的影响

从图7可知，在政府对制造商奖惩力度一定的情况下，产品碳排放量随着时间的递增而递减且逐渐趋于稳定；在一确定时刻时，产品碳排放量随着政府奖惩力度的增大而减小，说明可以采取政府奖惩机制激励企业减排投资的积极性。从图8可知，产品碳排放量随着它的自然增长率ω的增大而增大，且随着政府奖惩力度的增大而减小，说明当产品碳排放量的自然增长率较大时，会在一定程度上阻碍企业减排投入的积极性，此时政府可以通过增大碳排放奖惩力度激励企业进行减排投入。

4 结论

考虑到政府对制造商生产过程中产生的碳排放进行奖惩的情况下，本文从动态视角研究了供应链长期合作减排与低碳宣传问题。考虑到产品碳排放量随时间的推移存在自然增长的情况，且需求受碳排放量和低碳宣传努力的综合影响下，通过构建分散式和集中式微分博弈模型，并对模型进行求解与分析可得结论如下：

(1)分散式和集中式微分博弈情形下产品碳排放量最优轨迹均具有多种敛散情况；在一定条件下，两种情形下产品碳排放量最优轨迹均逐渐递减且趋于稳定值，此时集中式决策下零售商最优低碳宣传努力、产品需求量和供应链总利润较分散式决策时都有所提高，而产品碳排放量较分散式决策时都有所降低；说明集中式决策时不但兼顾环境而且可提高供应链利润，从而使企业的核心竞争力得到提高。

(2)随着碳排放量对制造商减排努力的敏感性以及碳排放量对需求的影响性的增大，产品碳排放量呈下降趋势；表明碳排放量对减排努力变化越敏感、消费者低碳消费意识越强，则供应链具有越好的合作减排效果。

(3)随着制造商的减排成本系数以及产品碳排放量自然增长率的增大，碳排放量呈上升趋势；表明供应链成员的单位减排成本投入越高，阻碍其自身的减排积极性，产品碳排放量上升。而当企业已投入的减排设备越容易自然老化(碳排放量自然增长率越大)时，供应链纵向合作减排效果越差；此时可通过实施政府奖惩政策降低制造商生产过程中的碳排放，且奖惩力度越大，供应链合作减排效果越好。 本文侧重研究企业低碳宣传投入、减排投入以及政府奖惩措施对供应链企业合作减排效果和利润的影响情况。但是未考虑除低碳宣传外的其他促销手段，且未考虑多个竞争性制造商参与减排，今后值得对这方面进行深入研究。