考虑损失厌恶行为与谈判破裂的Rubinstein谈判博弈研究

冯中伟， 谭春桥

(1.河南理工大学 能源科学与工程学院,河南 焦作 454000； 2.中南大学 商学院，湖南 长沙 410083)

0 引言

Rubinstein谈判[1]是一种处理两人之间如何进行利益分配的非合作博弈方法。无破裂风险与理性参与人是Rubinstein谈判两个突出的特征。然而，无破裂风险并不能准确地刻画现实的谈判过程，因为在现实的谈判问题中谈判破裂随时会发生。谈判破裂的原因无外乎两种：一种是参与人对漫长的谈判过程感到厌烦，愤而退出谈判；另一种是第三方的出现。前者如朝鲜退出朝核六方会谈事件；后者如高通收购恩智浦的提案由于未获得中国同意而致使该并购终止。另一特征——理性参与人亦有其局限性，因为人们更倾向于最小化其损失，而不是最大化其收益[2～5]。在谈判过程中，如果过去某谈判阶段的出价高于当前谈判阶段的出价，那么参与人会拒绝当前谈判阶段的出价，因为当前谈判阶段的出价发生了损失(相对于过去某谈判阶段较高的出价)。这是所谓的“损失厌恶”现象。

Kahneman和Tversky与1979年提出了损失厌恶的思想，他们认为决策者的心理参考点能够影响其决策时的风险态度，从而导致了决策者的非理性决策。当面对比参考点低的收益时，人们往往表现出损失厌恶的态度；且损失导致效用的减少大于所得导致效用的增加，即面对同样的损失或获得，人们对损失更敏感。这些心理特征被Kahneman和Tversky称之为损失厌恶。相关实验研究显示：损失厌恶行为在谈判中扮演着重要作用，如Bazerman等[6]在谈判实验的过程中发现，因为人们具有损失厌恶行为，人们更易于对获得财产达成一致，而不是损失财产。Neale和Bazerman[7]以及Neale等[8]得到了相似的结论。为了将损失厌恶引入Rubinstein谈判博弈中，本文采用Shalev[9]提出的损失厌恶模型。在Shalev的损失厌恶模型中，参与人的偏好由基本效用、非负的损失厌恶参数以及参考点三者刻画；如果参与人的所得低于参考点，那么其效用等于基本效用减去负效用，其中负效用等于损失乘以损失恶参数。自从Shalev提出线性的损失厌恶模型，该损失厌恶模型受到学者的广泛关注，并在许多研究损失厌恶行为的文献中得到应用[9,10]。

相关的研究主要分为两类：固定参考点与内生参考点[11～13]。

目前在谈判问题中研究谈判破裂与损失厌恶影响的文献并不多。Binmore等[11]首先在Rubinstein谈判博弈中引入谈判破裂风险的思想，并探讨了与纳什谈判解之间的关系。然而，文献[11]在对谈判博弈展开研究时并未考虑参与人的损失厌恶行为。为研究损失厌恶对谈判结果的影响，Shalev[12]假定参考点是内生的，在两人Nash谈判引入了损失厌恶行为。Driesen等[13]在文献[12]的基础上研究损失厌恶对n人Nash谈判的影响。Driesen等[14]在Rubinstein谈判中引入了损失厌恶行为，假定参考点等于过去谈判阶段被拒绝的最高出价，研究损失厌恶对Rubinstein谈判博弈的影响。

通过文献研究发现，考虑损失厌恶行为的Rubinstein谈判博弈的相关研究存在如下特点：1)相关文献假定参考点是内生的。然而在某些实现的谈判中，参考点可能是外生给定的。例如，已参加了一家公司招聘的求职者应聘第二家公司时，该求职者会以第一家公司的薪资待遇为参考，与第二家公司进行薪资谈判。2)相关文献未考虑谈判破裂的情形，这限制了其在实际谈判问题中的应用。因此，本文考虑谈判具有破裂风险且参与人具有损失厌恶行为的Rubinstein谈判博弈，在参考点是外生的情形下，寻找该谈判博弈的子博弈完美均衡，研究谈判破裂概率与损失厌恶行为对该均衡解的影响。

1 模型构建

1.1 具有谈判破裂风险的Rubinstein谈判博弈

参与人1和2针对大小为1的“馅饼”如何划分展开谈判，所有可能的结果集为

Z=:{(z1,z2)∈R2|z1+z2=1,z1,z2≥0}

在时刻t∈T={Δ,2Δ,3Δ,…}(其中Δ为两次连续出价之间的时间间隔)谈判发生。令Todd={Δ,3Δ,…}和Teven={2Δ,4Δ,…}分别表示奇数时刻集合与偶数时刻集合。在时刻t∈Todd，参与人1出价(z1,z2)∈Z，参与人2决定是否接受该出价。在时刻t∈Teven={2,4,…}，参与人2出价，参与人1决定是否接受出价。如果出价(z1,z2)被接受，谈判结束，参与人i(i=1,2)所得份额为zi。如果出价被拒绝，那么谈判可能破裂，也可能继续到下一时刻，令谈判破裂的概率为p，则谈判继续的概率为1-p。如果谈判破裂，参与人1和2的支付为零，如果谈判一直进行，参与人的支付依然为零。令δ=exp(-βΔ)为参与人的贴现因子，其中β>0贴现率。如果t时刻参与人i所得份额为zi，那么参与人i的支付为δtzi。

1.2 损失厌恶

在1.1节描述了具有谈判破裂风险的Rubinstein谈判博弈，本节假定参与人具有损失厌恶行为。为刻画参与人的损失厌恶行为，假定参与人i(i=1,2)的份额zi的基本效用等于zi，低于参考点ri∈[0,1]的份额zi视为损失，相应的效用随着损失厌恶系数λi≥0的增大而减小。根据Shalev的损失厌恶模型[15]，参与人i评估份额zi的效用为

wi(zi,λi,ri)=(1+λi)zi-λimax{ri,zi}

(1)

由(1)式给出的效用函数与Tversky和Kahneman提出的价值函数是相似的。(1)式保留了价值函数的损失厌恶性质。对于(1)式，损失厌恶系数λi越大，意味着参与人i的损失厌恶水平越高。

尽管文献[12～14]研究了参考点内生的情形，但内生的参考点具有其局限性，因为在某些情形下参考点是外生的。例如，已参加了一家公司招聘的求职者参加应聘第二家公司时，该求职者会以第一家公司的薪资待遇为参考，与第二家公司进行薪资谈判。因此，本文假定谈判过程中参考点是外生的，并且假定参与人1和2的参考点小于或等于参与人的出价。否则参与人的出价总是被对方拒绝，谈判永远无法达成一致。

2 子博弈完美均衡的构建

为了构建子博弈完美均衡，考虑子博弈完美均衡满足如下性质：

性质1(无延迟) 无论参与人何时出价，其均衡出价总是被另一个参与人接受。

性质2(稳定性) 在均衡中，无论参与人何时出价，该参与人总是进行相同的出价。

以此改善自身的效用。因此

(2)

相似的，在偶数时刻，有

(3)

(4)

(5)

联立等(4)式和(5)式，得

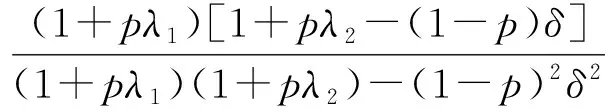
(6)

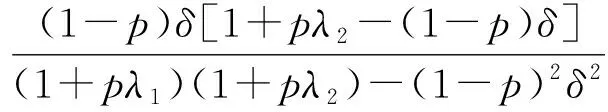
(7)

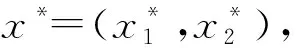
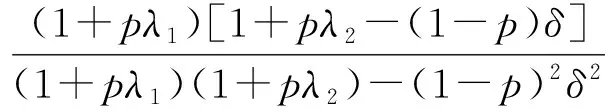
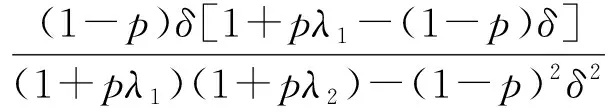
证明给定参与人2的策略(命题1中描述的策略)，证明参与人1的策略(命题1中描述的策略)是最优反应。

对于任意奇数时刻，参与人1出价z=(z1,z2)。存在三种情形：

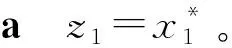
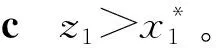
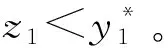
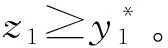
相似的，给定参与人1的策略(命题1中描述的策略)，证明参与人2的策略(命题1中描述的策略)是最优反应。证毕

如果λ1=λ2=0，那么x*=(1/[1+(1-p)δ],(1-p)δ/[1+(1-p)δ])，这是参与人是完全理性时的子博弈完美均衡出价。

如果λ1=λ2>0，那么x*=((1+pλ)/[1+pλ+(1-p)δ],(1-p)δ/[1+pλ+(1-p)δ])。

因为(1+pλ)/[1+pλ+(1-p)δ]>1/[1+(1-p)δ]。因此，参与人1受益于参与人2的损失厌恶行为。

令i=1,2。所有以参与人i开始出价的子博弈都是同构的。令Gi表示参与人i开始出价的子博弈。在任意时刻t∈T，令Mi=sup{zi:在子博弈Gi中存在一个子博弈完美均衡，在该均衡中参与人i的支付为zi}

mi=inf{zi:在子博弈Gi中存在一个子博弈完美均衡，在该均衡中参与人i的支付为zi}，其中M1和m1是在任意子博弈G1中任意子博弈完美均衡分配给参与人1的份额的上确界与下确界；M2和m2是在任意子博弈G2中任意子博弈完美均衡分配给参与人2的份额的上确界与下确界。

为证明命题1中所描述的策略是惟一的子博弈完美均衡，需要通过引理1～3建立M1、m1、M2和m2之间的关系。

引理1在具有损失厌恶行为与谈判破裂风险的Rubinstein谈判博弈中，存在

1)m1≥[1+pλ2-(1-p)δM2]/(1+pλ2)。

2)m2≥[1+pλ1-(1-p)δM1]/(1+pλ1)。

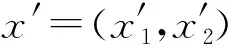
因此，对于任意的出价x=(x1,x2)，有x1≥[1+pλ2-(1-p)δM2]/(1+pλ2)换言之，m1≥[1+pλ2-(1-p)δM2]/(1+pλ2)。

相似的，可得m2≥[1+pλ1-(1-p)δM1]/(1+pλ1)。证毕

引理2在具有损失厌恶行为与谈判破裂风险的Rubinstein谈判博弈中，存在

1)m1≤[1+pλ2-(1-p)δM2]/(1+pλ2),M1≥[1+pλ2-(1-p)δm2]/(1+pλ2)。

2)m2≤[1+pλ1-(1-p)δM1]/(1+pλ1),M2≥[1+pλ1-(1-p)δm1]/(1+pλ1)。

证明如果m1>[1+pλ2-(1-p)δM2]/(1+pλ2),那么存在参与人2的出价z=(z1,z2)使得m1>[1+pλ2-(1-p)δz2]/(1+pλ2),这与m1的定义相矛盾，因此m1≤[1+pλ2-(1-p)δM2]/(1+pλ2)。

相似的，如果M1≤[1+pλ2-(1-p)δm2]/(1+pλ2),那么存在参与人2的出价z=(z1,z2)使得M1<[1+pλ2-(1-p)δz2]/(1+pλ2),这与M1的定义相矛盾，因此M1≥[1+pλ2-(1-p)δm2]/(1+pλ2),同理可证m2≤[1+pλ1-(1-p)δM1]/(1+pλ1)与M2≥[1+pλ1-(1-p)δm1]/(1+pλ1)。证毕

引理3在具有损失厌恶行为与谈判破裂风险的Rubinstein谈判博弈中，存在

1)M1≤[1+pλ2-(1-p)δm2]/(1+pλ2)。

2)M2≤[1+pλ1-(1-p)δm1]/(1+pλ1)。

证明在任意的子博弈G1中，在博弈的第一轮谈判中，参与人1出价z=(z1,z2)。如果参与人2拒绝参与人1的出价，那么博弈继续的情况下，在子博弈G1的第二轮谈判中，参与人2至少可以获得支付m2。因此在任意的子博弈完美均衡中，参与人2拒绝任意的出价z=(z1,z2)使得(1+λ2)z2-λ2max{r2,z2}<(1-p)δ[(1+λ2)m2-λ2max{m2,r2}]-pλ2max{r2,z2}。即:z1>[1+pλ2-(1-p)δm2]/(1+pλ2)。因此如果参与人1和2在第一轮谈判中达成一致，那么参与人1的支付不超过[1+pλ2-(1-p)δm2]/(1+pλ2)。

另一方面，如果参与人1的出价被拒绝，那么博弈以参与人2的出价y=(y1,y2)开始，记为G2。在博弈G2的任意子博弈完美均衡中，参与人1和2的均衡支付总和等于1，即y1+y2=1，这意味着y1≤1-m2。因此参与人1的支付不超过(1-p)δ(1-m2)。

综上所述，参与人1的支付不超过max{[1+pλ2-(1-p)δm2]/(1+pλ2),(1-p)δ(1-m2)}。因为max{[1+pλ2-(1-p)δm2]/(1+pλ2),(1-p)δ(1-m2)}=[1+pλ2-(1-p)δm2]/(1+pλ2),所以参与人1的支付不超过[1+pλ2-(1-p)δm2]/(1+pλ2)。因此，M1≤[1+pλ2-(1-p)δm2]/(1+pλ2)。

同理可得M2≤[1+pλ1-(1-p)δm1]/(1+pλ1)。证毕

定理2在具有损失厌恶行为与谈判破裂风险的Rubinstein谈判博弈中，命题1中描述的均衡策略是唯一的子博弈完美均衡。

证明如果定理2成立，则有

(8)

根据引理1～3，可得

M1=[1+pλ2-(1-p)δm2]/(1+pλ2)

(9)

m2=[1+pλ2-(1-p)δM2]/(1+pλ2)

(10)

M2=[1+pλ1-(1-p)δm1]/(1+pλ1)

(11)

m2=[1+pλ1-(1-p)δM1]/(1+pλ1)

(12)

联立(9)～(12)式，可得(8)式。

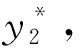
3 子博弈完美均衡的分析

本部分针对损失厌恶参数λ1和λ2以及谈判破裂的概率p对子博弈完美均衡进行敏感性分析。然后分析当p→0时均衡支付的收敛性，并将所建立的模型扩展至更一般的情形，即参与人1和2具有不同的贴现因子δ1和δ2，分析当两次连续出价的时间间隔Δ→0时，均衡支付的收敛性，并建立该极限均衡与非对称Nash谈判解的关系。

3.1 子博弈完美均衡的敏感性分析

根据定理1可知，谈判的结果为

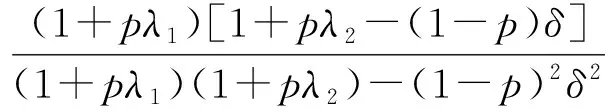
针对参与人1的均衡支付，求关于损失厌恶参数λ1的一阶偏导数

(13)

求关于损失厌恶参数λ2的一阶偏导数

(14)

因此，参与人1的均衡支付与自身的损失厌恶水平呈负相关关系，与参与人2的损失厌恶水平呈正相关关系。对于参与人2的均衡支付，存在相似的结论。

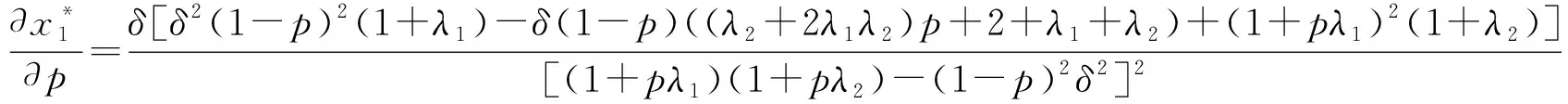
(15)

如果(1+λ2)/(1+λ1)>δ，那么参与人1的均衡支付随p的增加而增加；如果(1+λ2)/(1+λ1)<δ，那么存在临界值p*使得参与人1的均衡支付随p∈(0,p*]的增加而减少；随p∈(p*,1)的增加而增加。

3.2 子博弈完美均衡的收敛性

首先分析当谈判破裂的概率p→0时，均衡支付的收敛性。

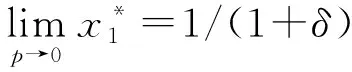
(16)

(16)式是经典的Rubinstein谈判博弈的结果。换言之，当谈判破裂的概率p→0时，具有损失厌恶行为与谈判破裂风险的Rubinstein谈判博弈结果收敛于经典的Rubinstein谈判博弈结果。

当参与人1和2具有不同贴现因子时，参与人i的贴现因子记为δi=exp(-βiΔ)，其中i=1,2，βi为参与人i的贴现率。等式(2)和(3)转化为

(17)

(18)

根据(17)和(18)式，可以得到满足性质1和2的子博弈完美均衡，该均衡是唯一的。参与人1和2的均衡出价分别为

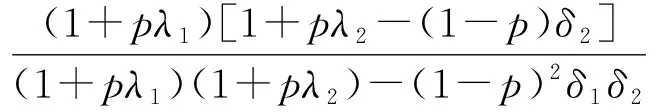
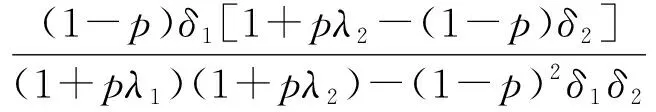
为了分析当Δ→0时子博弈完美均衡的收敛性，根据文献[15]，当Δ→0时，谈判破裂的概率p→0；比值p/Δ存在，且当Δ非常小时，p/Δ=τ，其中τ>0。因此，可得

同理，可得

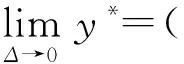
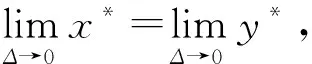
容易验证∂α/∂λ1<0和∂α/∂λ2>0。因此参与人1的议价能力与λ1呈负相关关系，与λ2呈正相关关系。同理，可推断参与人2的议价能力与λ1呈正相关关系，与λ2呈负相关关系。

对α求关于τ的一阶偏导数，得

如果β1/β2>(1+λ1)/(1+λ2)，那么∂α/∂τ>0，这意味着参与人1的议价能力随着τ的增加而增加；如果β1/β2<(1+λ1)/(1+λ2)，那么∂α/∂τ<0，这意味着参与人1的议价能力随着τ的增加而减小。

4 算例分析

为了更清楚地说明损失厌恶参数与谈判破裂风险对子博弈完美均衡的影响，本节通过数值分析进行说明。

具有损失厌恶行为的参与人1和2，针对如何分配1单位收益的问题进行交替出价谈判。谈判结果如定理1中所述。为简化，只分析损失厌恶参数以及谈判破裂风险对参与人1均衡支付的影响。令δ=0.6，p=0.2，损失厌恶参数λ1与λ2对参与人1均衡支付的影响如图1所示。令δ=0.6,λ1=14,λ2=2。谈判破裂概率p对参与人1均衡支付的影响如图2所示。

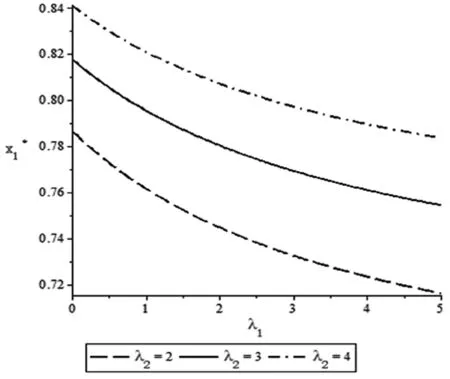
图1 λ1与λ2对参与人1均衡支付的影响

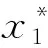
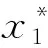
5 结论

Rubinstein基于期望效用理论研究了交替出价谈判博弈，然而现实的谈判问题中，谈判破裂的可能性随时发生；而且大量研究表明参与人可能表现出损失厌恶的行为特征。基于此，本文研究了具有损失厌恶与谈判破裂风险的Rubinstein谈判博弈。构建子博弈完美均衡，通过假设子博弈完美均衡满足无延迟性与稳定性两条性质，证明了该均衡的唯一性。通过对子博弈完美均衡进行关于损失厌恶与谈判破裂概率的敏感性分析，发现参与人受益于对手的损失厌恶行为，而因自己的损失厌恶行为遭受损失；均衡结果与谈判破裂概率之间的关系取决于贴现因子与参与人的损失厌恶水平。进一步发现当出价的时间间隔趋于零时，极限均衡结果收敛于非对称的Nash谈判解。本文研究的谈判博弈模型不仅丰富了谈判理论，而且更符合实际的谈判情形，结果具有更强的解释力，因而具有更强的理论价值与应用价值。本文通过假设子博弈完美均衡满足无延迟性与稳定性两条性质，证明子博弈完美均衡是唯一的，但是当子博弈完美均衡不满足这两条性质时，是否依然具有唯一性，有待进一步的研究。