随机波浪力连续场的降维模拟

吕康玄，刘章军

(1.三峡大学 土木与建筑学院，湖北 宜昌 443002；2.武汉工程大学 土木工程与建筑学院，湖北 武汉 430074)

海洋工程结构在其建设与服役过程中，可能遭受波浪、风、地震及海流等多种灾害作用，而波浪力是海洋工程结构的主要控制荷载之一。一般地，考虑到波浪力具有显著的时空动态特性，工程中通常采用连续随机场理论来描述随机波浪力。国内外学者多以Morison 方程[1]为基础研究波高谱与波力谱的关系，该理论认为波浪力可视为由未受扰动波浪场产生的拖曳力和惯性力组成。1958 年Borgman[2]对拖曳力进行了线性化处理，形成了线性化波浪力分析系统。1967 年Borgman[3]又将线性化的Morison 方程与谱分析相结合，从而建立了波高谱与波力谱的联系。1992 年俞聿修[4]从方差谱密度变换的角度给出了波力谱的类似形式，并基于P-M 谱对质点水平速度均方根值予以简化，其计算结果与原谱误差较小。以上方法多是从激励响应的角度，利用传递函数直接刻画了波高谱与波力谱之间的关系。而在波浪力数值模拟方面，Han 等[5]采用P-M 谱和Morison 方程建立了随机波浪力计算模型，并以海上柔性塔结构为例进行验证。Mardfekri 等[6]基于线性不规则波理论对海洋随机波浪进行了模拟，同时结合Morison 方程对单桩基础波浪荷载进行计算，提出了概率需求模型。武昕竹等[7]基于Fluent 软件对直立圆柱聚焦波浪进行了数值模拟。

上述随机波浪力的生成多以Monte Carlo 方法为基础，往往需要大量的随机抽样，计算量大，且难以形成完备的概率集。文献[8-9]从数学建模角度引入随机函数的约束，实现仅用1～2 个随机变量便可精确模拟离散状态下波浪力随机过程。为此，本文在推导随机波浪力的功率谱密度函数时，引入随机函数思想，并结合FFT 算法实现了仅用1 个随机变量便可精确模拟波浪力随机过程，且生成的代表性波浪力样本具有完备的概率集，从而可结合概率密度演化理论[10-11]对连续波浪力作用下的结构动力响应与可靠度进行精细化分析。

1 随机波浪力的谱密度

随机波浪力的谱分析法是利用波浪力的频率响应函数，由已知的波高谱推求作用于建筑物上的波浪力谱。本文将从平稳随机过程自相关函数的角度，对波高谱与波浪力谱之间的关系进行分析，进而导出随机波浪力的谱密度。

根据Morison 方程，单个小尺度直立桩柱上的随机波浪力是由包含速度项的拖曳力和包含加速度项的惯性力两部分组成：

式中： KD=0.5CDρD ， KI=0.25CIρπD2， CD和 CI分别为拖曳力系数和惯性力系数，根据《港口与航道水文规范》（JTS 145—2015），可取CD=1.2，CI=2.0； ρ为 海水密度； D 为桩柱直径；u (z,t)和 a (z,t)分别是水质点的水平速度和水平加速度，它们都是零均值的平稳随机过程，其功率谱密度函数[12]分别为：

式中：Sη(ω)为 波浪随机过程η (t) 的功率谱密度，即波高谱；z 是 以海底为坐标原点的竖向坐标；ω和 k 分别为频率和波数，它们之间满足弥散关系ω2=gktanh(kh)， 其中g 为 重力加速度， h为海水深度。

根据Borgman 的线性化处理[2]，得到：

式中：σu(z)为 水平速度过程u (z,t)的均方差，即：

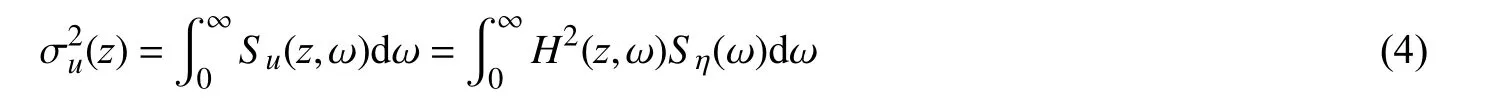
将式（3）代入式（1）中，得到随机波浪力的等价线性表达式：

考察随机波浪力的自相关函数，对于任意位置z 处的波浪力随机过程，其自相关函数为：

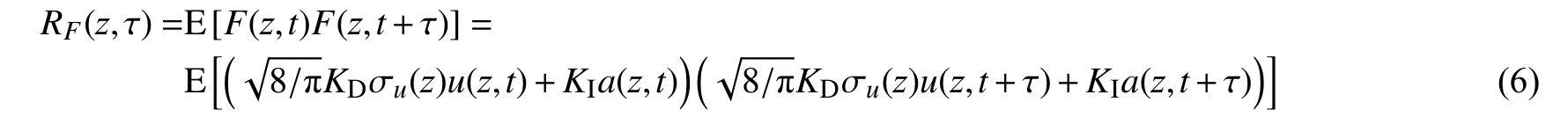
式中：τ 为时间间隔。E[·]表示取均值，根据平稳随机过程与其均方导数在同一时刻t 上总是互不相关的理论，可得：

根据自相关函数与功率谱密度函数之间的关系，得到：

式（8）为任意位置坐标z 处的波浪力功率谱密度函数。因此，随机波浪力是一个零均值的平稳随机过程，可以直接应用随机过程的谱表示法来模拟任意给定位置z 处的波浪力过程，从而实现随机波浪力连续场的高效模拟。

2 基于源谱表达的降维模拟

由于任意给定位置坐标z 处的波浪力是一个零均值的实平稳随机过程，根据平稳随机过程的谱表示理论，其源谱表达式为：

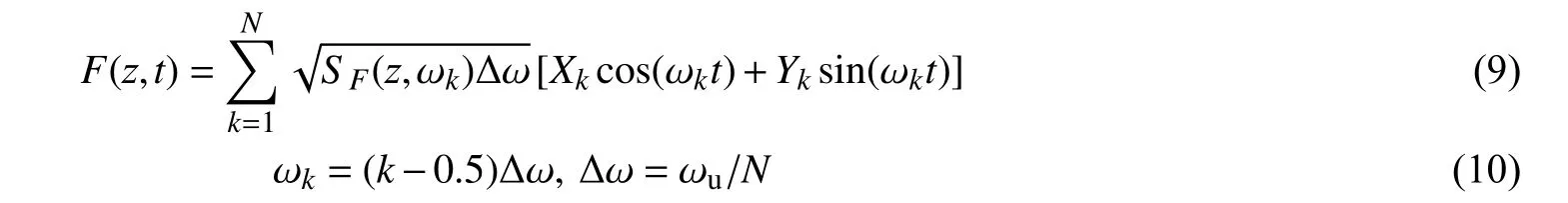
式中： ωk为第k 个离散点的频率； ∆ω 为频率步长； N 为频率截断项数； ωu为 截断频率；{ Xk,Yk}为一组标准正交随机变量，满足以下基本条件：

式中： δjk为Kronecker 记号。

如果直接假定式（9）中的标准正交随机变量集 {Xk,Yk}为一组相互独立的标准高斯随机变量，则式（9）就是所谓的非确定性幅值谱表示法，此时波浪力连续场的随机度为 2N，这种高维的随机度问题，对于非线性随机动力学是一个挑战。为此，考虑到随机变量集 {Xk,Yk}仅 需满足式（11）的基本条件，其概率分布未知，因此可以引入随机函数，实现随机波浪力连续场的降维模拟。首先，定义一组标准正交随机变量集为基本随机变量 Θ的正交函数：

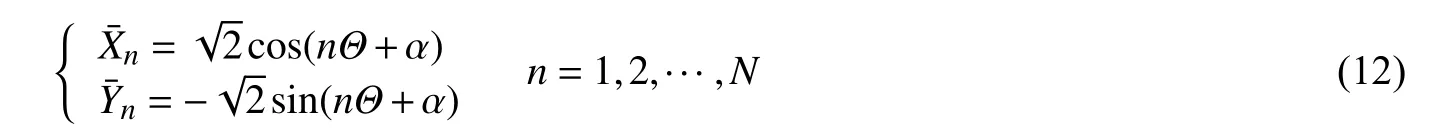
式中： Θ为基本随机变量，服从( −π,π)上 的均匀分布； α为 任意确定性参数，通常可取α =π/4。

其中，ϕk(Θ)为 基本随机变量 Θ的函数，其表达式为：

为保证模拟精度，定义任意给定位置坐标z 处波浪力过程的截断误差为：

一般地，ε (N)≪1， 对于随机波浪力连续场的模拟，本文建议ε (N)≤0.001。

在小学语文教学过程中运用经典诵读对于课堂教学效率与教学质量的提高、小学生阅读能力与写作能力的提升等方面具有重要的促进作用。综上所述，在小学语文教学中运用经典诵读是促进学生语文综合素养养成的重要途径。

3 随机波浪力连续场的FFT 算法

为进一步提高模拟效率，本文将FFT 算法[14]应用于随机波浪力连续场的模拟中。首先，将式（13）改写成如下形式：

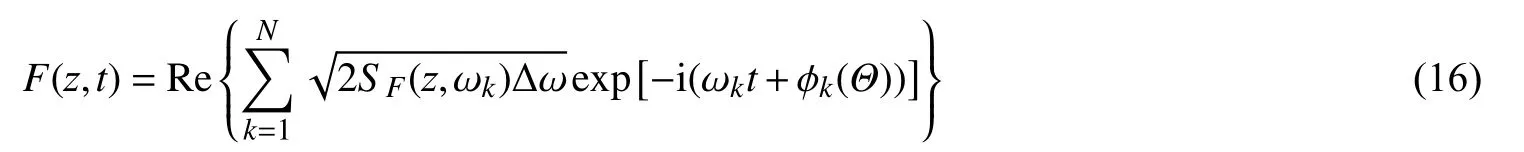
式中：R e[·]表 示取实部，i为虚数单位。

将时间t 进行离散，取时间步长为 ∆t，离散步r=1,2,…,2N, 则式（16）可进一步写成：

其中

为避免随机过程模拟失真，频率步长 ∆ω满足如下要求[15]：

在FFT 算法中，通过构建频率步长和时间步长之间的联系，能够将频率求和与时间离散同步进行，因而可极大地提高随机波浪力连续场的模拟效率。

4 数值算例

为了进一步阐述本文方法的有效性，以某一单个小尺度直立圆柱桩所受的随机波浪力进行分析。现以桩底为原点，海底平面水平方向为 x轴 ，竖直方向为 z轴，建立如图1 所示的坐标系。

式中：无因次常数µ =8.1×10−3，β =0.74； 重力加速度g =9.81 m/s2； v19.5表示海面上19.5 m 高度处的平均风速。

对于Pierson-Moscowitz 谱，式（4）可近似地简写为[4]：

其中， H1/3为1/3 有效波高，可按下式计算：

数值算例中具体参数如下：圆桩直径3 m，海水深24 m，海水密度为1 025 kg/m3，模拟持时1 000 s，平均风速16.24 m/s，频率截断项数1 024，FFT 变换点数2 048，频率步长0.006 28 rad/s，时间步长0.488 s，计算最大截断误差为2 .72×10−13。

为生成随机波浪力的代表性样本集合，首先需要对基本随机变量 Θ在 (−π,π)上 选取代表性点集其中 nsel为代表性点的数量（本文中 nsel=200 ），并计算每一个代表性点 θi的赋得概率 Pi。显然，所有代表性点的赋得概率之和为了说明本文方法的有效性，分别采用降维模拟方法和Monte Carlo 方法生成200 条随机波浪力样本，计算得到均值误差、标准差误差及模拟时间分别为0.059%(5.750%)，3.43%(3.94%)和11.97 s(12.07 s)。可见，降维模拟方法的均值误差远小于Monte Carlo 方法，标准差误差也略小于Monte Carlo 方法，表明降维模拟方法具有较高的模拟精度。此外，在模拟效率方面，降维模拟方法也略优于Monte Carlo 方法。

图2 给出了降维模拟方法与Monte Carlo 方法生成的第100 条随机波浪力样本函数（以 z=17 m 为例）。由图2 可知，上述两种方法生成的波浪力样本函数在幅值、波长等方面具有相似性，且均具有零均值平稳随机过程的基本特征。

图2 随机波浪力的样本函数Fig.2 Sample functions of random wave force

图3 绘出了随机波浪力在时间和空间两个维度上的分布，其中从z=0.01 m 起，取高度间隔为0.01 m，利用本文方法生成2 400 个桩柱位置处的随机波浪力代表性样本，并取各桩柱位置处的第1 条代表性样本绘制而成。从图3 可知，沿着桩柱的高度方向，波浪力的幅值逐渐增大，且在靠近海平面位置处波浪力幅值增长的速率加快；而在时域方向，波浪力表现出显著的零均值特征和平稳特征。

图4 为模拟的均值及标准差与目标值比较（以z=17m 为例）。从图4 可以看出，模拟的均值、标准差均与目标值一致。图5 给出了 z=17 m 处随机波浪力的自相关函数比较。

图3 不同高度处波浪力代表性时程三维图Fig.3 3-D figure of representative time-histories for wave force at different heights

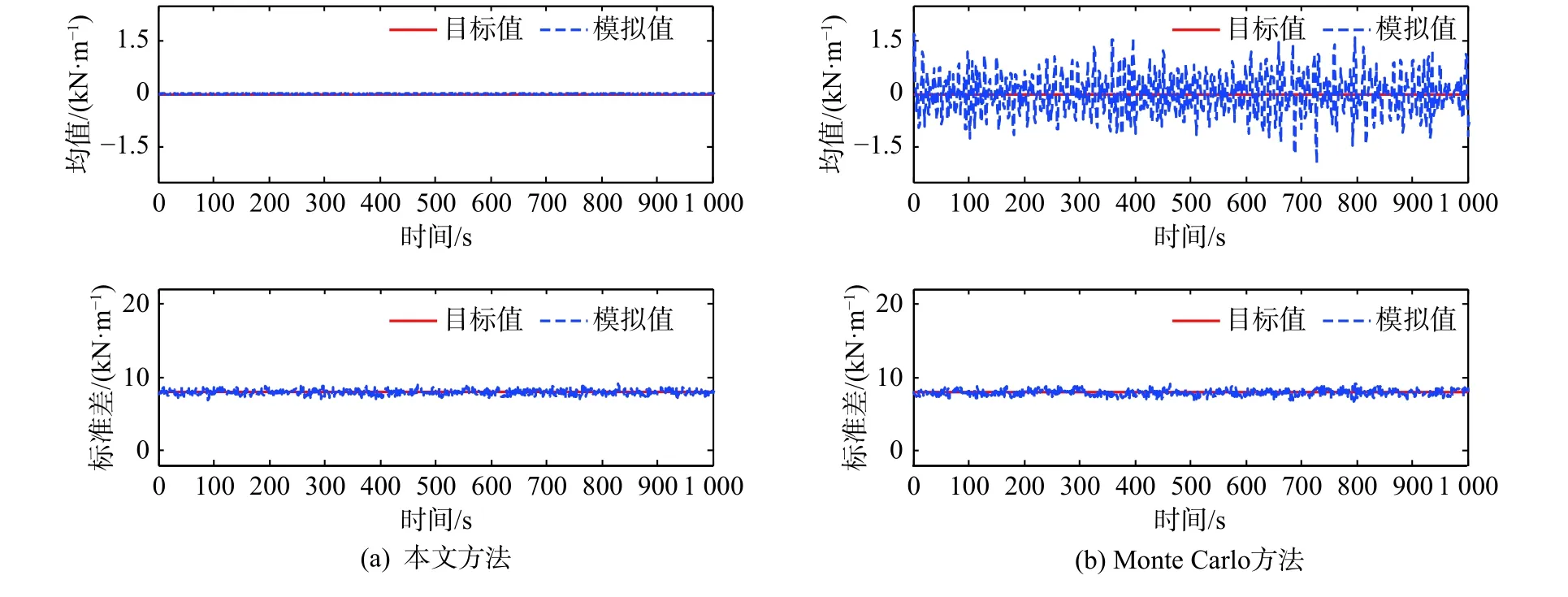
图4 z =17 m处均值及标准差比较Fig.4 Comparison of mean and standard deviation atz=17 m

图5 z =17 m处自相关函数比较Fig.5 Comparison of auto-correlation functions atz=17 m

图6 为z1=17 m 和 z2=21 m之间的互相关函数比较，其中自（互）相关函数均进行了无量纲处理。显然，自相关函数和互相关函数的模拟值与目标值几乎完全拟合，进一步说明了降维模拟方法的有效性。

图7 进一步给出了本文方法与Monte Carlo 方法关于相干函数的比较。图中以 z1=17 m 和 z2=21 m处的两个随机波浪力过程为例，在有效频率0.4～2.8 rad/s范围内，计算其相干函数的模拟值和目标值。从图7可见，在有效频率范围内，模拟的相干函数值在目标值上下波动，且比Monte Carlo 方法的结果更接近于目标值，表明本文方法的模拟精度更高。

图6 z1=17 m 和z2=21 m处互相关函数比较Fig.6 Comparison of cross-correlation functions between z1=17 m andz2=21 m

图7 z1=17 m 和z2=21 m处空间相干函数比较Fig.7 Comparison of spatial coherence functions between z1=17 m andz2=21 m

5 结 语

本文利用线性化的Morison 方程，从平稳随机过程自相关函数的角度推导出随机波浪力的功率谱密度函数。同时，在平稳随机过程的源谱表达基础上，结合随机函数的降维思想，建立了随机波浪力连续场的降维模型。研究表明，该降维模型具有以下特点：

（1）利用任意高度处随机波浪力的功率谱密度函数，实现了用1D-1V 平稳随机过程的谱表示理论模拟2D-1V 随机波浪力连续场的目的。本质上，本文方法是一种连续的方法，可以对任意高度处的随机波浪力进行快速模拟，避免了传统离散方法对于模拟点数量和位置的限制。

（2）基于随机函数的降维思想，实现了仅用1个基本随机变量即可精细地模拟随机波浪力连续场。与Monte Carlo 方法相比，本文方法生成的代表性样本能够构成一个完备的概率集，在模拟效率和精度方面也略高于Monte Carlo 方法。