复杂河道边界对滑坡涌浪周期的影响

王梅力，祖福兴，徐绩清，王平义，韩林峰

(1.重庆交通大学 国家内河航道整治工程技术研究中心，重庆 400074；2.重庆交通大学 建筑与城市规划学院，重庆 400074；3.重庆市交通规划勘察设计院，重庆 400074)

滑坡涌浪是滑坡体滑入江河湖海后，将所携带能量在水体中进行充分转换而激起的巨大波浪。滑坡涌浪是滑坡的次生灾害，但对涌浪生成区域和传播区域所造成的灾害非常巨大，有时甚至超过了滑坡本身[1-4]。河道型水库滑坡涌浪的一个显著特点就是河道边界对涌浪传播的作用。当滑坡涌浪传播到达河道边界时，部分涌浪被反射而形成反射波，而反射波与相继而来的入射波会发生叠加，叠加后的波高会很大，往往对河道中的船舶及岸边的建筑造成二次灾害。而河道的边界往往是非常复杂的，河道岸边的坡度各不相同，引起涌浪的反射率不同，形成的反射周期也会不同；直线河岸与曲线河岸会影响波浪的反射角度，反射波的方向会不同，不同的平面曲率和圆弧角度都会影响反射波周期。

目前国内外有关河道边界对滑坡涌浪周期的研究较少，Law 等[5]定性地对滑坡涌浪的传播规律进行了研究，结合试验数据分析推导出滑坡涌浪的传播距离和衰减程度成反比的规律；Risio 等[6-7]建立了圆形岸坡的库区滑坡涌浪模型，以此为基础研究了圆形岸坡涌浪的爬高规律，对滑坡涌浪的三维流场进行了深入研究；王育林等[8]对峡谷型河道的危岩崩滑所产生的静态和动态破坏进行了分析，对滑坡给水工建筑物、航道及航行船舶带来的危害进行了论述；胡小卫[9]考虑到库岸滑坡的多发性与危害性，通过研究水库滑坡成因和产生涌浪的各方面影响因素，以三峡水库为依托，建立了水槽概化模型，通过控制富裕水深、有效接触面积和滑坡坡度3 个因素，计算滑坡涌浪的各项特性；杨飞鹏[10]采用数值模拟方法，研究了在两种截面形状以及含有弯道情况下滑坡涌浪的传播与衰减规律；谢海清等[11]利用FLOW-3D 计算仿真工具建立了数值模型，用于对狭窄型库区河道的滑坡涌浪的产生、传播进行模拟研究，对滑坡产生的初始浪高和传播过程中的浪高衰减规律进行了公式拟合；黄筱云等[12]利用FLOW-3D 计算流体力学软件，建立了数值模型模拟滑坡体沿着斜坡下滑后产生涌浪以及传播的过程，用以研究V 型河道中产生的滑坡涌浪的爬高及传播特点。本文基于FLOW-3D 计算流体力学软件建立三维滑坡涌浪数值模型，模拟分析滑坡体入水点位于河道直线段、弯道凸岸顶点、弯道凹岸顶点情形下，复杂河道边界对滑坡涌浪周期的影响规律，对深入揭示滑坡涌浪传播特性及其灾害防控具有重要的意义。

1 数值模拟研究方法

本文采用的水动力学控制方程是连续性方程和不可压缩黏性流体运动的Navier-Stokes 方程，将流体视为不可压缩黏性流体，即：

流体的动量守恒定律由运动方程（N-S 方程）来描述，即：

式中：ρ 为流体密度（kg/m3）；Ax，Ay，Az分别代表流体在x，y，z 方向单元面内流体可流过区域的面积分数；u，v，w 分别为x，y，z 方向上的速度分量（m/s）；VF为单元内流体可流动区域的体积分数；Gx，Gy，Gz分别为流体在x，y，z 方向上的质量力加速度（m/s2）；fx，fy，fz分别为流体x，y，z 方向上的黏滞力加速度（m/s2）。

FLOW-3D 中的紊流模型包含普朗特混合长度模型、k-ε 方程模型、LES 模型、ε 方程模型、RNG k-ε 模型5 种紊流模型来模拟紊流。本文采用RNG k-ε 紊流模型[13]计算涌浪的产生和传播。采用有限差分法对控制方程进行离散。

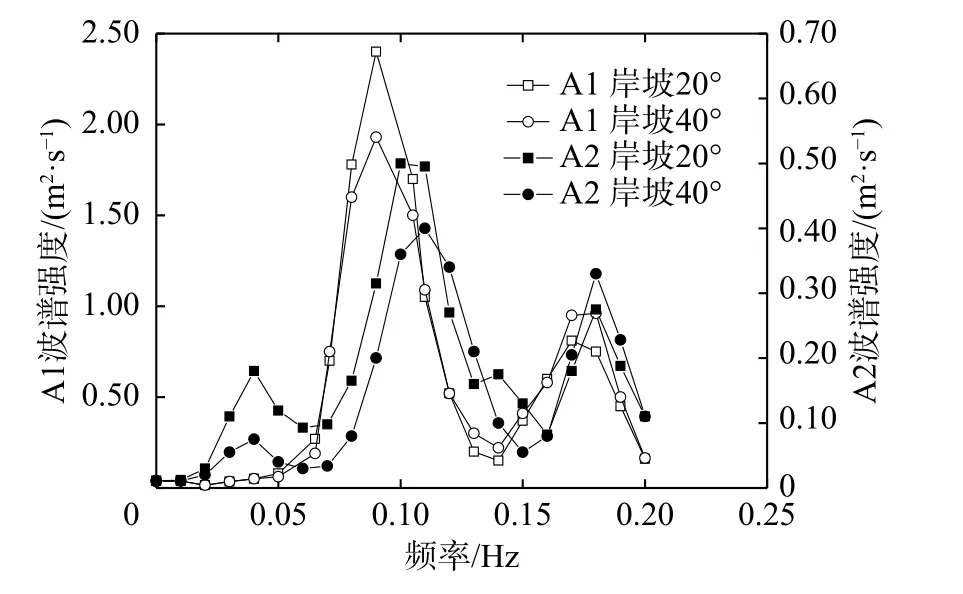
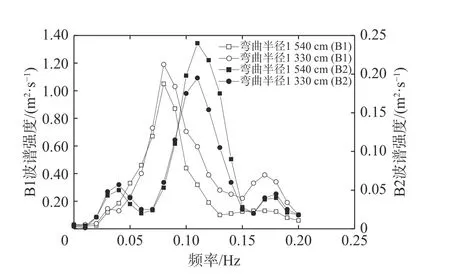
VOF 法是一种处理复杂自由表面的有效方法，其基本思想是：在任何一个计算区域内，水和气体的体积分数之和为1，定义F 为计算区域内水占区域的流体分数，在FLOW-3D 中，对于某个计算网格单元而言：F=1表 示计算网格单元内充满水体， F=0表 示计算网格单元内充满气体， 0

2 模型的建立与验证

2.1 模型的建立

选取与长江三峡库区万州某河段原型一致的物理模型[14]。以试验中的1 个工况为例，物理模型尺寸为560 m（河宽）×51.8 m（水深），对岸岸坡为20°。河道凹岸弯曲半径为1 120 m，河道凸岸弯曲半径为560 m，河道弯曲角度为90°，滑坡面倾角选取40°。滑坡体尺寸选取70 m×35 m×14 m。构建的河道和滑坡体三维模型如图1(a)所示。模型采用六面体结构化网格，在滑块落水处采用渐变网格加密，x 方向网格最小尺寸0.1 m，最大0.2 m；y 方向网格尺寸均为0.1 m；z 方向尺寸均为0.1 m，如图1(b)所示。

图1 滑坡涌浪数值模拟三维模型及网格划分Fig.1 3D model and mesh of landslide surge numerical simulation

网格块包含的区域为计算区域，由于该网格块为长方体，因此6 个面都需要给定边界条件，该区域上表面为自由表面，采用压力边界条件，给定水面压力p=1.013×105Pa；由于物理模型试验是在静水中进行，因此其余表面边界条件采用无滑移壁面WALL 条件，水工建筑物视为混凝土材质，糙率为0.014。

2.2 模型验证

以物理模型试验结果[14]对数值模拟结果进行验证。选择在顺直河道进行模型试验，河道实际水位取145 m，对应河道实际水深51.8 m，滑坡面倾角选择40°，滑坡体尺寸选取70 m×35 m×14 m，波高测点共布置16 个，如图2 所示。各测点物理试验换算成原型的结果与数值模拟试验结果对比见图3。

图2 凸岸滑坡涌浪测点平面布置（单位：m）Fig.2 Layout plan of swell measuring points of convex landslide (unit: m)

从图3 可以看出：数模计算结果与物模实测结果的最大偏差为4.94%，平均偏差为4.06%。说明FLOW-3D对滑坡涌浪的产生及传播的模拟具有较高精度，可用于复杂边界对滑坡涌浪周期的影响研究。

3 河道边界对滑坡涌浪周期的影响

3.1 岸坡坡度对滑坡涌浪周期的影响规律

为了模拟分析岸坡坡度对滑坡涌浪周期的影响规律，选取滑坡体处河对岸岸坡坡度为20°和40°进行对比。以图2 滑坡入水点向对岸做垂线，在垂线上靠近滑坡入水点处设置A1 测点（对应图2 中1#测点），在垂线上靠近对岸坡脚处设置A2 测点（对应图2 中5#测点）。A1 测点靠近滑坡入水点，此处的涌浪周期主要受入射波控制，反射波起次要作用。A2 测点靠近河对岸岸坡坡脚处，此处的涌浪周期主要受反射波控制，入射波起次要作用。试验完成后，提取A1 测点和A2 测点随时间的水位变化值，利用傅里叶自相关离散型光谱频率函数[15]，通过Matlab 编程，绘制A1 测点和A2 测点频谱图（图4）。

从图4 可以看出，入射波起主导作用的A1 测点，包括两个控制波周期，即主控制波周期T11（T11=1/0.09=11.11 s）和辅控制波周期T12（T12=1/0.18=5.56 s）。反射波起主导作用的A2 测点，包括3 个控制波周期，即T21（T21=1/0.04=25.00 s），T22（T22=1/0.11=9.09 s）和T23（T23=1/0.18=5.56 s），3 个控制波周期中T22的波谱强度最大。A2 测点的T23周期和A1 测点的T12周期相同，涌浪波谱强度前者比后者低，说明A2 测点的T23周期的涌浪是由A1 测点的T12周期的涌浪传播衰减而来。而A2 测点的T21和T22周期的涌浪是由A1 测点的T11周期演变而来。A1 测点的T11周期的涌浪到达对岸岸坡后分成了两部分：一部分爬高后反射回来，经爬高反射后造成这部分周期延长，就成为了A2 测点的周期为T21的波浪；另一部分破碎后反射回来，经破碎反射后造成这部分周期缩短，就成了A2 测点的周期为T22的波浪。对比20°和40°两种不同的岸坡坡度，前者的破碎后反射波浪较后者的大，表明岸坡坡度越小，涌浪破碎数量越多。

图4 不同岸坡坡度作用下A1 及A2 测点频谱Fig.4 Spectra of point A1 and point A2 under the action of different bank slope angles

3.2 弯曲河道凹岸对滑坡涌浪周期的影响规律

3.2.1 凹岸平面曲率对滑坡涌浪周期的影响规律

选取凹岸弯曲半径分别为1 330 和1 540 m，即平面曲率1/1 330 和1/1 540 进行对比试验。滑坡入水点选取弯道凸岸中间点临水处，以滑坡入水点向对岸做垂线，在垂线上靠近滑坡入水点处设置B1 测点，在垂线上靠近对岸坡脚处设置B2 测点。利用前述方法绘制1#和2#测点频谱图（图5）。

从图5 可见，入射波起主导作用的B1 测点，包括两个控制波周期，即主控制波周期T11（T11=1/0.08=12.50 s）和辅控制波周期T12（T12=1/0.18=5.56 s）。反射波起主导作用的B2 测点，包括3 个控制波周期，即T21（T21=1/0.04=25.00 s），T22（T22=1/0.11=9.09 s）和T23（T23=1/0.18=5.56 s），3 个控制波周期中T22的波谱强度最大。B2 测点的T23周期和B1 测点的T12周期相同，涌浪波谱强度前者比后者低，说明B2 测点的T23周期的涌浪是由B1 测点的T12周期的涌浪传播衰减而来。而B2 测点的T21周期和T22周期的涌浪是由B1 测点的T11周期演变而来。B1 测点的T11周期的涌浪到达对岸岸坡后分成了两部分：一部分爬高后反射回来，经爬高反射后造成这部分周期延长，就成为了B2 测点的周期为T21的波浪；另一部分破碎后反射回来，经破碎反射后造成这部分周期缩短，就成了B2 测点的周期为T22的波浪。对比平面曲率1/1 330 和1/1 540 的凹岸河道边界，两者的最大主控制波周期均是由T11（T11=1/0.08=12.50 s）变化到T22（T22=1/0.11=9.09 s），表明不同平面曲率的凹岸河道边界，对涌浪周期的影响是相同的，均是整体性略微缩短。

3.2.2 凹岸圆弧角度对滑坡涌浪周期的影响规律 选取凹岸圆弧角度分别为30°和90°进行对比试验。B1 测点和B2 测点的位置同3.2.1，利用前述方法绘制B1 测点和B2 测点频谱图（图6）。

图5 不同凹岸平面曲率作用下B1 及B2 测点频谱Fig.5 Spectra of point B1 and point B2 under the action of plane curvature of different concave banks

从图6 可以看出，入射波起主导作用的B1 测点，包括两个控制波周期，即主控制波周期T11（T11=1/0.09=11.10 s）和辅控制波周期T12（T12=1/0.18=5.56 s）。反射波起主导作用的B2 测点，包括3 个控制波周期，即T21（T21=1/0.04=25.00 s），T22（T22=1/0.1=10.00 s）和T23（T23=1/0.18=5.56 s），3 个控制波周期中T22的波谱强度最大。B2 测点的T23周期和B1 测点的T12周期相同，涌浪波谱强度前者比后者低，说明B2 测点的T23周期的涌浪是由B1 测点的T12周期的涌浪传播衰减而来。而B2 测点的T21周期和T22周期的涌浪是由B1 测点的T11周期演变而来。B1 测点的T11周期的涌浪到达对岸岸坡后分成了两部分：一部分爬高后反射回来，经爬高反射后造成这部分周期延长，就成为了B2 测点的周期为T21的波浪；另一部分破碎后反射回来，经破碎反射后造成这部分周期缩短，就成了B2 测点的周期为T22的波浪。对比圆弧角度为30°和90°的凹岸河道边界，两者最大的主控制波周期均是由T11（T11=1/0.09=11.10 s）变化到T22（T22=1/0.1=10.00 s），表明不同圆弧角度的凹岸河道边界，对涌浪周期的影响是相同的，均是整体性略微缩短。

图6 不同凹岸圆弧角度作用下B1 及B2 测点频谱Fig.6 Spectra of point B1 and point B2 under action of different concave bank arc angles

3.3 弯曲河道凸岸对滑坡涌浪周期的影响规律

选取凸岸圆弧角度分别为60°和90°进行对比试验。将滑坡入水点由凸岸中间坡脚临水处移至凹岸中间坡脚临水处，以滑坡入水点向对岸做垂线，在垂线上靠近滑坡入水点处设置C1 测点，在垂线上靠近对岸坡脚处设置C2 测点。同前述方法，绘制C1 测点和C2 测点频谱图（图7）。

从图7 可以看出，入射波起主导作用的C1 测点，包括两个控制波周期，即第一控制波周期T11（T11=1/0.08=12.50 s）和第二控制波周期T12（T12=1/0.2=5.00 s）。反射波起主导作用的C2 测点，包括3 个控制波周期，即T21（T21=1/0.04=25.00 s），T22（T22=1/0.11=9.09 s）和T23（T23=1/0.18=5.56 s）。涌浪到达对岸岸坡后，由于凸岸边界的特殊性，受到的影响异常激烈。但总的来说分成了两部分：一部分爬高后反射回来，经爬高反射后造成这部分周期延长；另一部分破碎后反射回来，经破碎反射后造成这部分周期缩短。

图7 凸岸作用下C1 及C2 测点频谱Fig.7 Spectra of point C1 and point C2 under convex bank action

4 结 语

（1）选取与长江三峡库区万州某河段为原型一致的物理模型，基于计算流体力学FLOW-3D 软件，建立了滑坡涌浪三维数值模型，经与物理模型试验验证符合性较好。按照滑坡入水点位于河道直线段、弯道凸岸顶点、弯道凹岸顶点3 种工况，计算模拟分析了复杂河道边界对滑坡涌浪周期的影响规律。

（2）靠近滑坡入水点的涌浪周期主要受入射波控制，反射波起次要作用；靠近滑坡体对岸岸坡坡脚处的涌浪周期主要受反射波控制，入射波起次要作用。对比20°和40°两种不同的岸坡坡度，前者的破碎后反射波浪较后者的大，表明岸坡坡度越小，涌浪破碎数量越多。

（3）不同平面曲率的凹岸河道边界，对涌浪周期的影响相同，均是整体性略微缩短。不同圆弧角度的凹岸河道边界，对涌浪周期的影响也均是整体性略微缩短。

（4）由于凸岸边界的特殊性，涌浪到达对岸岸坡后，总体上分成了两部分：一部分爬高后反射回来，延长了波周期；另一部分破碎后反射回来，这部分的波周期缩短。