三峡枢纽下游引航道水力波动叠加效应研究

程 龙，李 云，安建峰

(1.南京水利科学研究院 通航建筑物建设技术交通行业重点实验室，江苏 南京 210029；2.河海大学 水利水电学院，江苏 南京 210098)

水利枢纽运行过程中因流量变化引起的河道和引航道中的水位波动属于典型的河渠非恒定流现象[1]。三峡枢纽兼具防洪、发电及航运等功能，建有升船机、船闸等通航建筑物。为满足防洪、发电需求，枢纽在运行过程中切换运行工况，下泄流量变幅和变率较大，从而引起河道、引航道中波流运动[2-3]。引航道内的波流运动易导致升船机承船厢附近水面波动较大，水位变化速率较快，不仅会降低升船机运行效率，而且会对船舶的安全航行、升船机承船厢对接以及承船厢误载水深控制等产生不利影响[4-5]，直接关系到升船机的运行安全性和通过能力，对其展开深入细致研究意义重大。

枢纽非恒定流水力波动的相关研究发展迅速。针对三峡枢纽下游引航道非恒定流的研究，主要有原型观测、模型试验和数值模拟等方法[1,6-7]。对于河势复杂的天然河道中重力长波运动的模拟，通常情况下一维非恒定流计算模型已能满足计算精度和效率要求。其中，基于显式格式的特征线数值算法和基于偏心差分格式的Preissmann 四点隐式差分算法在计算模拟中应用最为广泛。

本文针对三峡枢纽下游引航道水力波动问题，考虑葛洲坝枢纽的反调节作用，重点研究三峡枢纽下游引航道水力波动叠加规律以及水力要素对波动特性的影响。

1 工程概况

三峡升船机布置在三峡枢纽左岸永久船闸的右侧，其下游引航道宽80～90 m，长2 700 m，在距离船闸下闸首1 100 m 处与船闸引航道汇合后共用一条引航道连通长江主河道。升船机引航道与船闸引航道的两个盲端，具有显著的“盲肠”效应，枢纽泄洪、电站日调节、船闸泄水及下游葛洲坝枢纽反调节对三峡枢纽下游引航道内水力波动影响较大。

三峡枢纽调度原则为兴利调度服从防洪调度、发电调度与航运调度相互协调并服从水资源调度；葛洲坝水利枢纽调度任务为对三峡枢纽日调节下泄的非恒定流进行反调节。两坝间最大通航流量为56 700 m3/s，三峡枢纽下游通航水位73.8～62.0 m，葛洲坝坝前水位变化范围一般控制在66.5～63.0 m。三峡枢纽的运行调度原则，仅针对三峡船闸的运行要求制定。然而升船机运行对引航道水位波动幅值控制要求更加苛刻，现有的调度原则即便在通航允许的流量和水位范围内，也很难满足不大于0.5 m/h 的水位变率限制。故而本文旨在明确引航道波动机理，揭示枢纽运行条件下的水力波动叠加规律，以便在今后的运行调度中实现波动预警和安全调控。以三峡-葛洲坝两坝间主河道及三峡下游引航道为研究区域进行数值模拟研究（图1）。

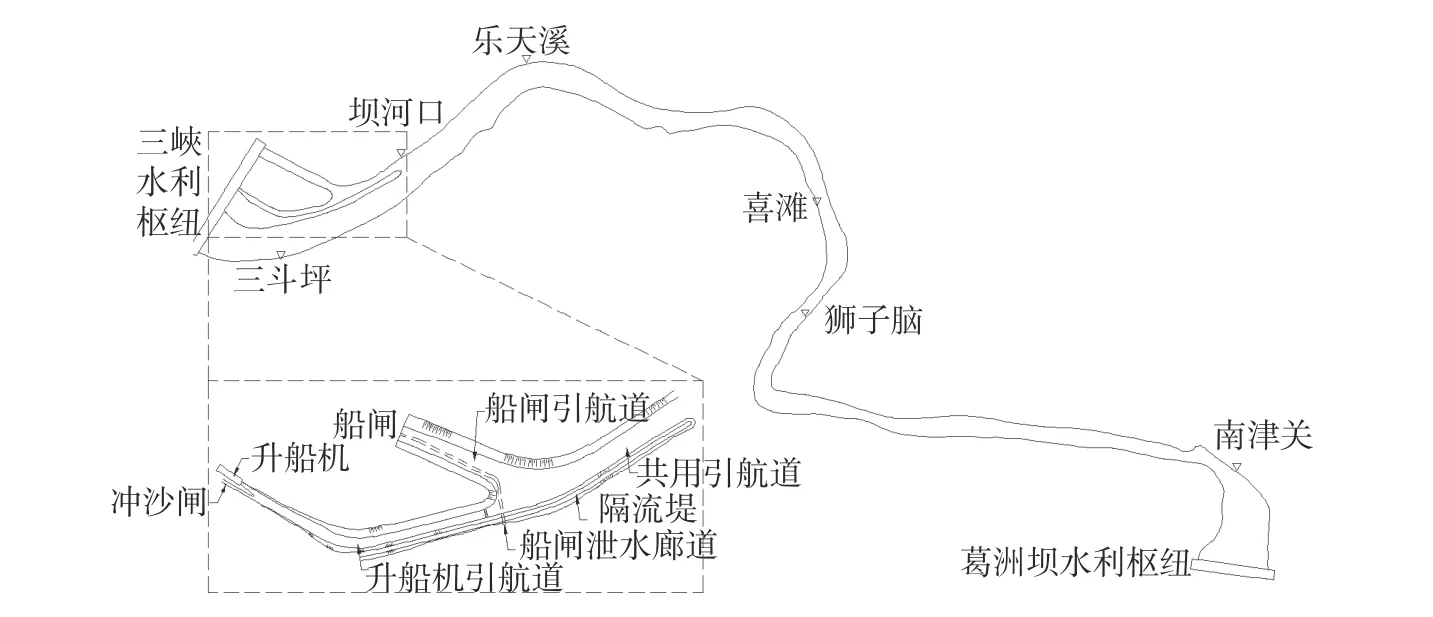
图1 研究区域示意Fig.1 Schematic diagram of study area

2 数学模型

2.1 控制方程和数值算法

一维明渠非恒定流基本方程包括连续方程和动量方程。

连续方程：

动量方程：

式中：B 为水面宽度；z 为水位；Q 为流量；x 为流程；q 为旁侧入流单宽流量；t 为时间；A 为过水断面面积；g 为重力加速度；J 为水力坡度。

控制方程是非线性双曲型偏微分方程，采用Preissmann 四点隐式差分格式将控制方程离散为代数方程组，求其数值解。Preissmann 四点隐式差分格式逼近为：

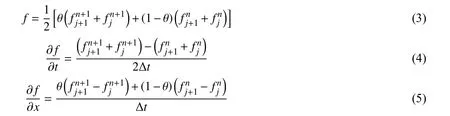
式中：f 为任意函数；j，j+1 为沿空间（x）方向节点；n，n+1 为时间（t）方向节点；θ 为时间权重因子，当θ≥1/2 时，计算无条件稳定。

2.2 计算区域与边界条件

计算区域为三峡-葛洲坝两坝间主河道及三峡下游引航道（图1）。综合考虑数值计算条件和提高计算精度的需要，计算域差分离散断面间距取为5 m，共有计算断面7 700 个。对河道和引航道的转弯点、交汇点、盲端等典型断面，共设置38 个控制点，输出流量、水位等水力要素。

上游边界（三峡枢纽）给定离散的流量数据，下游（葛洲坝枢纽）边界条件视研究工况而定，可给定离散的流量或水位数据。对于盲端边界，则以流量为零作为边界条件，对于引航道分岔或交汇点，以支路总水头相等作为控制条件。

2.3 模型率定和验证

模型参数的率定主要考虑糙率的取值。糙率的取值对计算结果中河道比降影响较大，但对于波动的相对波高及其变率影响较小。本文关注点主要是后者，故在糙率取值时，参考了三峡-葛洲坝两坝间水情信息以及文献资料中所载的河道比降，两坝间各河段的平均综合糙率一般在0.028～0.033。根据水情实测数据与计算所得河道比降对比验证，取河道平均综合糙率为0.03，计算准确度能够满足研究需要。

通过三峡-葛洲坝两坝间水情信息数据对数学模型进行验证，如图2 所示。图2（a）为边界条件，图2（b）为该边界条件下升船机下闸首水位波动的原型观测和数学模型计算结果对比。

图2 数学模型计算结果与原型观测结果对比Fig.2 Comparison of the results of mathematical model calculation and prototype observation

由图2 可知，基于Preissmann 四点隐式差分格式的数学模型计算结果与原型观测数据总体趋势一致，小振幅波动周期基本一致。这说明数学模型对模拟两坝间非恒定流作用下的引航道水位波动具有较好的精度，可以用于引航道及河道水位波动特性的模拟研究。

3 引航道水力波动叠加规律

应用上述数学模型，计算如下工况引航道口门及升船机下闸首水位波动过程：河道初始流量5 000 m3/s，葛洲坝坝前初始水位63.0 m，三峡枢纽流量在30 min 内线性增加2 000 m3/s，葛洲坝枢纽分别取流量不变和敞泄（敞泄时流量变化方式与三峡枢纽相同），计算结果见图3。分析计算结果可见，当下游枢纽流量不变时，水位波动过程由枢纽流量调节引起的泄水推进波及河道涨水波动过程组成；当下游枢纽敞泄时，可以看作河道涨水为零，即水位波动由泄水推进波和振荡衰减过程组成。

进一步分析图3 可知，引航道口门的波动过程与河道波动过程相同，主要由两坝间净流量所引起的平均涨水过程和以其为平衡轴的振荡过程叠加而成。升船机下闸首水位波动过程则表现为引航道口门波动过程和引航道内往复波流的叠加。鉴于此，定义参数如下：引航道口门相对水深 he=ze−ze0，引航道口门水位相对波动 ∆he=ze−，升船机下闸首相对水深 hl=zl−zl0，升船机下闸首水位相对波动∆hl=hl−he。其中： ze和 ze0分别为引航道口门水位及其初始值；为引航道口门平均水位； zl和 zl0分别为升船机下闸首水位及其初始值。

图3 计算工况水位过程线Fig.3 Hydrograph of the calculated working condition

河道水位振荡过程（引航道口门水位波动过程滤去河道平均涨水过程）呈现明显的振幅逐渐衰减的正弦波特性，波动周期约1.4 h。引航道内往复波流（升船机下闸首水位波动过程中滤去引航道口门水位波动过程）同样表现为振幅逐渐衰减的正弦波特性，波动周期约0.67 h。当葛洲坝枢纽敞泄时，两坝间净流量为零，平均涨水过程线斜率为零，其他特性与以上描述相同。

同理，当上游枢纽下泄流量小于下游枢纽时，两坝间水位持续下降，河道波动过程主要由两坝间净流量所引起的平均落水过程和以其为平衡轴的振荡过程叠加而成，波动叠加的其他规律相似。

4 水力要素与波动特性的响应关系

由式（1）和（2）可知，影响波动特性的水力要素主要有河道糙率、河道基流、初始水位、上游枢纽流量变幅和变率。对于三峡枢纽下游引航道内的波动而言，河道糙率是确定的，而枢纽流量变率由枢纽运行方式决定，现有运行方式也是确定的。由于流量变幅较大时，河道涨、落水过程对波动坦化作用较强，故引航道及河道相对波动很小，水位变化过程主要取决于涨落水速度。计算结果表明，流量变幅大于4 000 m3/s 时，相对波动第一幅值与变幅为2 000 m3/s 时的相差不大，波动衰减速率更快。因此，本文仅就河道基流和初始水位的影响进行详细阐述，且由于减流量与增流量在规律上是相似的，故本文以增流量为例进行研究。

4.1 河道基流影响

数值计算的边界条件和初始条件：河道初始流量5 000～40 000 m3/s，三峡枢纽流量30 min 线性增加2 000 m3/s，葛洲坝坝前初始水位63.0 m，葛洲坝枢纽分别取流量不变和敞泄。

葛洲坝枢纽流量不变的情况下，计算结果（图4）显示，不同基流条件下，引航道口门及升船机下闸首水位波动趋势基本一致。基流越小，引航道口门及升船机下闸首水位变化趋势越陡，说明河道平均涨水过程随基流增加而减小。另外，计算结果也表明基流对波动幅值影响不大。

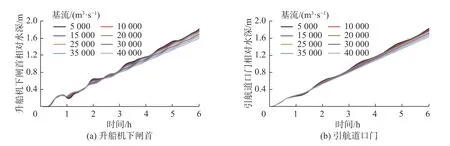
图4 不同基流条件下的水位波动Fig.4 Fluctuation of water level under different base flows

引航道口门水位相对波动幅值 Ae和升船机下闸首水位相对波动幅值 Al随基流的变化（图5）显示，二者的变化趋势可由指数函数表示：

式中：Ax为波动幅值（ Ae或 Al）；a，b 为与水力要素有关的系数。

图5 不同基流条件下水位相对波动幅值变化Fig.5 Changes of relative water level fluctuation amplitude under different base flows

葛洲坝枢纽敞泄的情况下，水位相对波动幅值同样满足式（6）的函数关系。上述各种情况下，式（6）中系数的取值与基流 Q0的关系见表1。

表1 不同基流条件下相对波动幅值变化规律Tab.1 Change law of relative fluctuation amplitude under different base flow conditions

4.2 初始水位影响

数值计算的边界条件和初始条件：河道初始流量5 000 m3/s，三峡枢纽流量30 min 线性增加2 000 m3/s，葛洲坝坝前初始水位63.0～66.5 m，葛洲坝枢纽分别取流量不变和敞泄。

葛洲坝枢纽流量不变的情况下，引航道口门水位相对波动幅值 Ae和升船机下闸首水位相对波动幅值Al随初始水位的变化如图6。初始水位对引航道口门水位相对波动影响不大。但是，初始水位对升船机下闸首相对波动幅值有一定影响，波动衰减速率也随初始水位增加而降低。

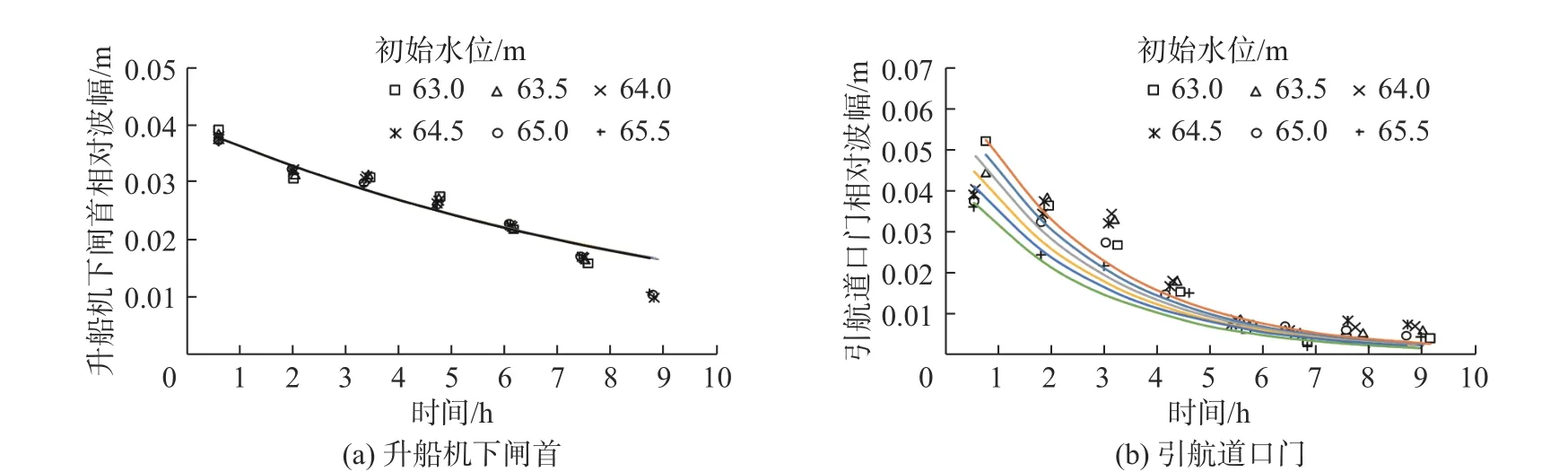
图6 不同初始水位条件下水位相对波动幅值变化Fig.6 Changes of relative water level fluctuation amplitude under different initial water levels

葛洲坝枢纽敞泄的情况下，计算结果显示的规律与葛洲坝枢纽流量不变时相似。两种情况下，相对波动幅值变化均满足式（6）的函数关系，系数与初始水位的关系见表2。

表2 不同初始水位条件下相对波动幅值变化规律Tab.2 Change law of relative fluctuation amplitude under different initial water levels

5 水力波动过程回归分析

结上所述，引航道口门和升船机下闸首的相对波动幅值随时间的变化关系均满足式（6）。在下标中用字母e 和l 区分引航道口门和升船机下闸首的参数，用字母s 和c 区分葛洲坝枢纽流量固定不变和敞泄时的参数。对波动衰减特性中的系数a 和b 进行回归分析。对引航道口门处水位波动，得到： aes=0.04，bes=−2×10−5Q0；aec=0.15，bec=−3×10−5Q0−0.1。 对升船机下闸首水位波动，得到：als=4×10−6Q0−0.01z0+0.695，bls=6×10−6Q0−0.41；alc=2×10−6Q0−0.027 4z0+1.879 3，blc=−0.35。

因为引航道口门水位波动过程是河道平均涨落水过程与其相对波动的叠加，且相对波动波形与正弦波一致，故葛洲坝枢纽流量不变和敞泄时引航道口门水位波动过程可表示为：

式中：c 为流量调节速率；k 为小时涨水速率； ωe=πC/L ，L 和C 为河道长度和平均波速； ta为流量调节时间；∆Q为流量变幅。

类似地，升船机下闸首水位波动过程是引航道口门水位过程与其相对波动的叠加，且相对波动波形与正弦波一致，故葛洲坝枢纽流量不变和敞泄时引航道口门水位波动过程可表示为：

式中：ωl=πCl/Ll， Ll和 Cl为引航道长度和平均波速。

根据式（7）～（10），计算得到三峡初始流量5 000 m3/s，葛洲坝坝前初始水位63.0 m，三峡枢纽流量在45 min内线性增加3 000 m3/s，葛洲坝流量不变（5 000 m3/s）和敞泄（流量过程与三峡枢纽一致）情况下引航道口门及升船机下闸首水位波动过程，并与相应工况的数值模拟结果进行对比，如图7 和8 所示。

图7 引航道口门相对水深变化过程回归分析与数值计算结果对比Fig.7 Comparison of results between regression analysis and numerical calculation of changing process of relative depth at approach channel entrance

图8 升船机下闸首相对水深变化过程回归分析与数值计算结果对比Fig.8 Comparison of results between regression analysis and numerical calculation of changing process of relative depth at lower head of ship lift

由图7 可知，葛洲坝流量不变时，引航道口门水位波动、升船机下闸首水位波动的数值计算结果和回归分析结果吻合度很好，两处的相对水深最大差别分别不超过0.04 和0.06 m。这说明滤波方法能有效计算出两处的水位波动过程。根据图8，葛洲坝敞泄时，波动起始阶段，由于泄水推进波作用，引航道口门水位上升时间大于1/4 周期，故图中波动回归分析时以统一周期计算会使该时段水位过程与计算结果有一定差异；升船机下闸首水位波动的数值计算结果和回归分析结果吻合度良好。

应用数学模型和式（7）～（10）的回归结果，对两坝间不同基流、不同流量差以及三峡枢纽不同流量变幅的情况进行了计算，结果发现：两坝间净流量不大于2 000 m3/s 时，升船机下闸首水位波动小时变幅均小于0.5 m，各工况能满足升船机运行要求，当净流量为3 000 m3/s 时，涨水过程中约60%的时间可满足升船机运行要求，但当净流量超过4 000 m3/s 时，整个涨水过程均超出升船机运行要求。

基于以上结果，在两枢纽联合调度时，应尽量控制两坝间净流量不超过2 000 m3/s；另一方面，当流量变幅超过2 000 m3/s，可采用升船机对接实时预警措施，利用口门区水位波动情况实时预报升船机下闸首波动情况[8]；还可考虑通过在引航道设置工程措施降低波动对升船机运行的影响。

6 结 语

本文就三峡枢纽下游引航道水力波动叠加问题进行了研究，得到结论如下：

（1）从明渠非恒定流基本方程出发，建立了Preissmann 四点隐式差分格式的数学模型，并结合原型观测资料进行验证，结果表明该数学模型对模拟两坝间非恒定流作用下的引航道水位波动具有较好的精度。

（2）研究了引航道波动叠加规律，引航道口门的波动过程主要由两坝间净流量所引起的平均涨水过程和以其为平衡轴的振荡过程叠加而成，升船机下闸首水位波动过程则表现为引航道口门波动过程和引航道内往复波流的叠加，河道水位振荡过程和引航道内往复波流均呈现振幅逐渐衰减的正弦波特性。

（3）分析了河道基流和初始水位对波动特性的影响，引航道口门、升船机下闸首水位相对波动幅值的衰减过程基本符合指数规律。

（4）通过回归分析，给出了葛洲坝枢纽流量不变和敞泄时三峡枢纽下游引航道口门和升船机下闸首的水位波动过程表达式，能有效获得枢纽非恒定流作用下引航道水位波动过程，具有较高的模拟精度。

（5）在两枢纽联合调度时，应尽量控制两坝间净流量不超过2 000 m3/s；当流量变幅超过2 000 m3/s，可采用升船机对接实时预警措施，利用口门区水位波动情况实时预报升船机下闸首波动情况；还可考虑通过在引航道设置工程措施降低波动对升船机运行的影响。