内部裂缝缺陷对混凝土断裂性能的影响

王思瑶，胡少伟

(1.南京水利科学研究院，江苏 南京 210029；2.武汉大学 水利水电学院，湖北 武汉 430072)

混凝土是现代土木工程中主要的建筑用材，因其自身特性及其各种因素引起的缺陷，对混凝土结构的安全性能有着重要影响[1-2]。裂缝作为混凝土结构内部最常见的缺陷会影响结构的力学承载性能。因此，研究混凝土材料中裂缝缺陷对断裂特性的影响具有重要意义。

断裂力学应用于分析混凝土材料断裂过程以来，带裂缝的混凝土试件包括中央带缺口的三点弯曲梁[3-4]、带初始裂缝的楔入劈拉试件[5-7]以及紧凑拉伸试件[8]随即成为主要的混凝土材料断裂力学性能测试试件。20 世纪80 年代，徐世烺与Reinhardt 等提出了双K 断裂模型[9-11]，模型通过引入混凝土材料的起裂和失稳韧度描述裂缝在混凝土材料中断裂的全过程，并提出测试水工混凝土断裂韧度的一般方法[12]。该测试方法被广泛用于工程中混凝土材料断裂力学行为的测试。

近年来，一些学者对缺陷影响材料断裂力学行为进行了研究。胡少伟等[13]利用内部预制孔洞缺陷的楔入劈拉试件分析了混凝土断裂力学测试试验中试件内部缺陷对其断裂力学测试结果的影响，认为当裂缝经过缺陷时会降低相关参数，当其远离缺陷区域时，则影响较小。胡少伟等[14]对含多条预置裂缝的混凝土三点弯曲试验梁的断裂过程进行了测试，试验结果得到次缝对试件测试中的结果具有重大影响。孙国有等[15]将细观空洞的扩张与I-II 复合型裂缝相结合并推导出其相应的断裂参数。

本文基于混凝土梁的三点弯曲断裂试验，在试件内部构建不同参数的贯穿裂缝缺陷，通过试验获得的断裂特征曲线结合双K 断裂模型计算获得其断裂参数与断裂能，并对计算结果进行对比分析，从而得到混凝土试件内部含裂缝缺陷及缺陷参数对断裂测试结果的影响。

1 试验概况

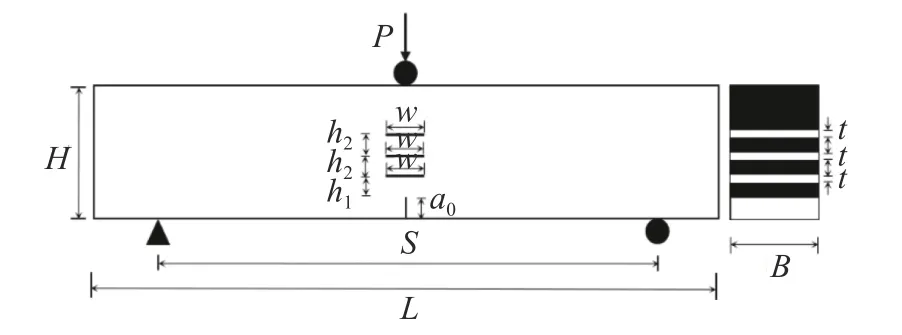
图1 试件尺寸Fig.1 Dimension of specimen

试验设计了10 组共30 个标准三点弯曲梁试件(S/H=4)，试件尺寸均为L×H×B=1 000 mm×200 mm×120 mm，其中含有n 个水平裂缝缺陷，试件形式如图1 所示。图中h1为边缘裂缝尖端至第1 个内部裂缝缺陷中心的距离，h2为两相邻内部裂缝缺陷的距离，其中内部裂缝缺陷中心均在边缘裂缝延长线上，w 为内部裂缝缺陷的长度，a0为边缘缝高度（本试验中设为40 mm），混凝土三点弯曲梁试件的裂缝设计参数见表1。

试件采用的混凝土由42.5 普通硅酸盐水泥、最大粒径为20 mm 的石灰岩碎石和天然河砂配制而成，配合比为水泥∶砂∶石∶水=1∶1.225∶2.485∶0.440。混凝土混合料在振动下浇注到木模中，试件边缘预制缝以及内部裂缝缺陷分别采用厚3 mm、一端为30°V 型和两端均为30°V 型的不锈钢板预埋，钢板在初凝后终凝前拔出。混凝土标准立方体试件28 d 龄期抗压强度、抗拉强度、杨氏模量和泊松比分 别 为：fc=46.7 MPa，ft=3.46 MPa，e=33.0 GPa 和μ=0.2。

混凝土三点弯曲梁试件的断裂测试试验在20 t电子伺服万能压力机上进行，试验现场装置如图2所示，试验中压力机的垂直加载速率小于10 N/s，试验加载前进行预加载以确保仪器及测试传感装置的准确连接。试验中所有试验数据采用DH5902 动态数据采集仪采集，采集的试验数据包括：由压力传感器获取的外加垂直荷载、由竖向位移计获取的试件中心竖向位移、由夹式引伸计获取的竖缝口张口位移、由应变片获取的竖缝裂尖应变和横缝上端应变（图3）。

表1 试件设计参数Tab.1 Design parameters of specimens

图2 试验装置Fig.2 Test device

图3 应变片分布Fig.3 Distribution of strain gauges

试件的破坏形态和断裂路径如图4 所示。可见水平裂缝缺陷在裂缝扩展路径上，且裂缝穿过水平裂缝缺陷后仍保持I 型的断裂模式扩展路径。

图4 试件断裂路径Fig.4 Fracture path of specimens

2 混凝土三点弯曲梁断裂性能参数计算方法

2.1 断裂参数计算方法

根据文献[9-11]，并结合《水工混凝土断裂试验规程》（DL/T 5332—2005）计算三点弯曲梁试件的断裂韧度。

式中：P 为外加荷载值；W 为试件支座间梁的自重，由试件总重量乘以S/L 计算得到；S 为试件两支座间的跨度；a 为裂缝长度；H，B 和L 分别为试件的高度、厚度和长度。

根据双K 断裂准则[11]，计算混凝土起裂韧度Kini时，仅需将起裂荷载Pini和边缘预制缝长度a0代入上述公式即可；计算混凝土失稳韧度Kun时，将失稳荷载Pun和临界有效裂缝长度ac代入上述公式即可。其中，ac按下式计算：

式中：h0为钢片刀口厚度；E 为计算弹性模量；Dmc为临界裂缝张口位移，即试件P-Dm曲线中峰值荷载Pmax所对应的值。其中，E 按下式计算：

式中：ci为试件初始Dm/P 值，由P- Dm曲线上升直线段上任一点的Dm和P 计算可得。

2.2 断裂能计算方法

根据三点弯曲梁试验测得的荷载-位移全过程曲线，采用RILEM(国际材料和结构试验室联合会)推荐的公式[16]计算混凝土的断裂能。

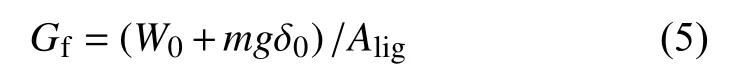
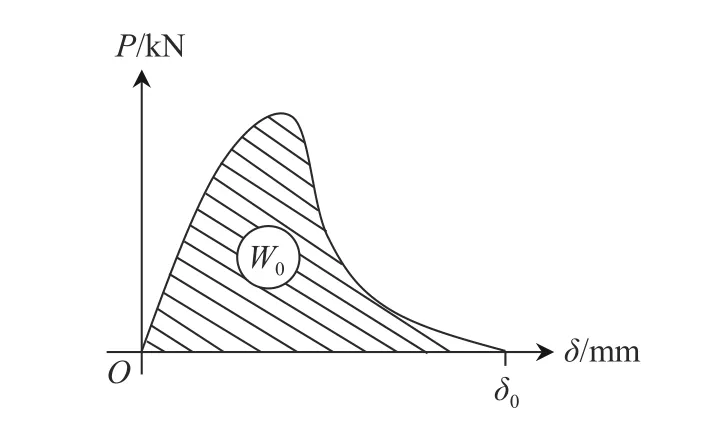
图5 P-δ 曲线Fig.5 P-δ curves

式中：W0为荷载-位移（P-δ）曲线下所围图形的面积（图5）；δ0为梁完全断裂时的加载点位移；m 为支座间梁的质量；g 为重力加速度，取为9.81 m/s2；Alig为混凝土梁断裂带在垂直于梁轴平面上的投影面积。Alig按下式计算：

式中：H 和B 分别为梁的高度和厚度；a0为边缘缝高度；n 为水平裂缝缺陷数量；t 为水平缺陷厚度。

3 水平裂缝缺陷对混凝土断裂性能的影响

3.1 水平裂缝缺陷长度对混凝土断裂性能的影响

图6 不同水平裂缝长度P- Dm 曲线Fig.6 P- Dm curves of different horizontal crack lengths

图6 给出了混凝土梁内部含不同长度水平裂缝缺陷的P-Dm曲线。可见，各组试件的P-Dm曲线规律相似，并且与无缺陷梁的曲线相似，即试件的断裂过程依然呈现出典型的三阶段式，分别为线弹性阶段、稳定扩展阶段和失稳扩展阶段。第1 阶段，混凝土梁中未出现裂纹，荷载与裂缝口张开位移呈线性关系；第2 阶段，随着荷载的增大，混凝土梁开始出现微裂纹并且形成断裂过程区，裂缝的张口位移增加速度加快，裂缝稳定扩展，P-Dm曲线呈非线性增长；第3 阶段，混凝土梁达到极限承载能力，试件中裂缝迅速扩展最终导致其完全断裂失效，在P-Dm曲线上表现为荷载突然降低同时张口位移迅速增加。由测得的P-Dm曲线，曲线峰值前的线性段至非线性段的拐点对应的荷载为起裂荷载Pini（同时也是预制缝尖端P-ε 曲线上应变最大值对应的荷载值），峰值对应的荷载以及裂缝口张开位移分别为失稳荷载Pmax和临界张口位移Dmc，同时根据式(1)～ (6)计算可得起裂韧度、失稳韧度以及断裂能。图7 给出了计算所得的断裂参数随水平裂缝长度的变化。随着水平裂缝缺陷长度从60 mm 增至120 mm，测试的混凝土梁起裂荷载Pini保持约为6 kN 不变，起裂韧度约为1 MPa·m1/2保持不变，而试件的失稳荷载Pmax从8.39 kN减到6.87 kN，减小了18.1%，失稳韧度从2.08 MPa·m1/2降至1.65 MPa·m1/2，降低约20%；断裂能Gf从85.29 N/m 降至70.43 N/m，降低了17.4%。计算结果表明，试件内部的水平裂缝缺陷对混凝土三点弯曲梁试件的起裂荷载和起裂韧度影响较小，但会加速试件失稳，并且水平裂缝的长度越长，裂缝扩展过程进入失稳破坏阶段越早。由试验测得的Pini/Pmax从0.72 增大到0.88 可知，水平裂缝缺陷的存在及其长度的增大使得断裂测试中试件断裂过程中的脆性也进一步增大。

图7 断裂参数随水平裂缝长度变化曲线Fig.7 Fracture parameters versus horizontal crack lengths

3.2 水平裂缝缺陷位置对混凝土断裂性能的影响

图8 给出了含不同位置水平裂缝试件的P-Dm曲线。由图8 可知，各组试件的P-Dm曲线呈相似规律，也与无水平裂缝缺陷试样的结果相似，各组试件的断裂过程表征出线弹性、裂缝稳定扩展和裂缝失稳扩展阶段。图9 给出了计算所得的断裂参数随水平裂缝位置的变化。由图9 可知，由于水平裂缝位置不同，断裂参数有所差异，具体表现为：水平裂缝缺陷位置h1从80 mm 降至20 mm，试件的起裂荷载Pini保持在6.05～6.11 kN，计算获得的起裂韧度保持在0.93～1.06 MPa·m1/2，而测得的失稳荷载Pmax从9.04 kN 降至7.45 kN，减少约17.6%，失稳韧度从2.09 MPa·m1/2减小到1.71 MPa·m1/2，约减小18.2%，试验测得断裂能Gf从86.59 N/m 降至66.26 N/m，减小约23.5%。试验结果表明水平裂缝缺陷与边缘预制缝尖距离h1越小，Pmax和越小，试件中裂缝进入失稳扩展阶段越快。又由Pini/Pmax从0.67 增大到0.82 可知，水平裂缝缺陷的存在及其距离h1的减小，试件的脆性不断增大，测得的断裂参数也越小。

图8 不同裂缝位置P-Dm 曲线Fig.8 P-Dm curves of different horizontal crack locations

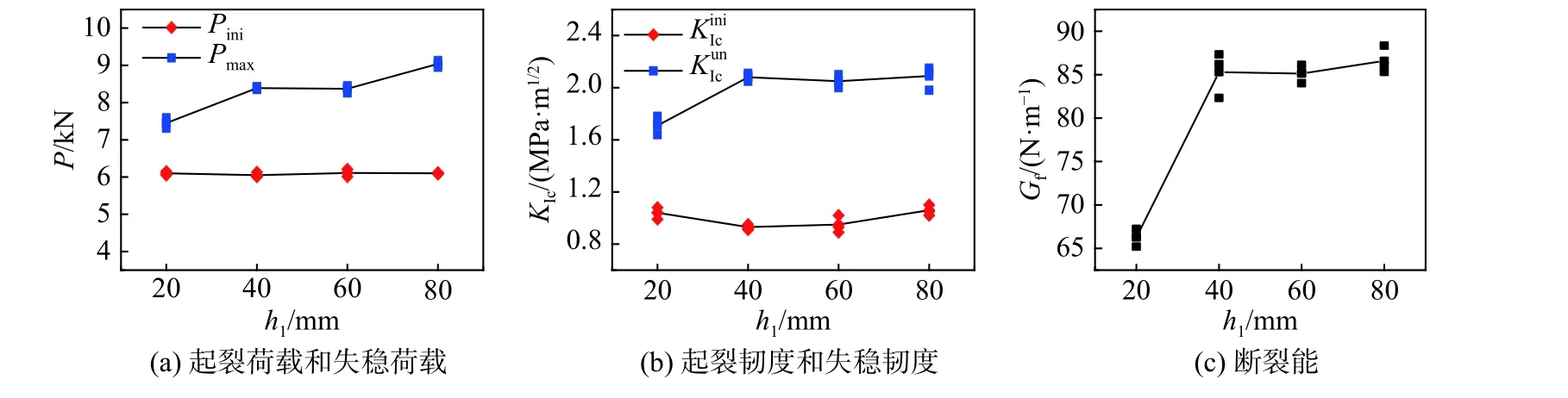
图9 断裂参数随水平裂缝位置变化曲线Fig.9 Fracture parameters versus horizontal crack locations

3.3 水平裂缝缺陷数量对混凝土断裂性能的影响

图10 给出了含不同水平裂缝缺陷数量的试件的P-Dm曲线。由图可知各组试件的P-Dm曲线呈相似规律，各组试件的断裂过程仍分为3 个阶段。图11 给出了计算所得的断裂参数随水平裂缝数量的变化。随着水平裂缝缺陷数量由0 增加至3，试件的起裂荷载Pini为5.94～6.05 kN，起裂韧度为0.93～1.09 MPa·m1/2，而试件的失稳荷载Pmax从9.11 kN 减到6.39 kN，失稳韧 度从2.15 MPa·m1/2降 至1.68 MPa·m1/2，降 低 了21.9%，断裂能Gf从88.5 N/m 降至70.45 N/m，降低20.4%。试验结果表明，由于水平裂缝缺陷的存在及其数量的增多，Pmax和均减小，Pini/Pmax从0.66 增大到0.93，试件更早进入失稳断裂过程，混凝土试件的脆性也不断增大。

图10 不同裂缝数量P-Dm 曲线Fig.10 P-Dm curves of different numbers of cracks

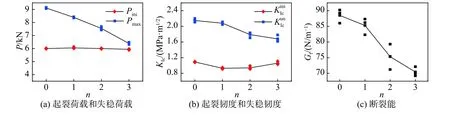
图11 断裂参数随水平裂缝数量变化曲线Fig.11 Fracture parameters versus number of horizontal cracks

4 结 语

试验设计了含不同类型水平裂缝缺陷的混凝土梁的三点弯曲断裂试验，主要研究不同长度、位置及数量的水平裂缝缺陷对混凝土断裂性能的影响。依据试验中测得的P-Dm曲线以及相关试验数据计算得到含不同裂缝缺陷混凝土断裂参数与断裂能，对比分析不同参量试件的测试结果，得到以下主要结论：

（1）混凝土内部的水平裂缝缺陷对三点弯曲梁试件的起裂荷载和起裂韧度测试结果影响较小，但是对失稳荷载和失稳韧度的测试结果影响较大。

（2）对含60，80，100 和120 mm 长度的水平裂缝缺陷的混凝土三点弯曲梁试件进行测试，结果表明断裂韧度和断裂能随裂缝缺陷长度的增加而降低，且裂缝长度由60 mm 增至120 mm 时，失稳韧度降低约20%，断裂能降低约17.4%。

（3）对距边缘预置缝缝尖20，40，60 和80 mm 水平裂缝缺陷的混凝土三点弯曲梁试件进行测试，结果表明断裂韧度和断裂能随裂缝缺陷距离的降低而降低，且距离位置由80 mm 减至20 mm 时，失稳韧度降低约18.2%，断裂能降低约23.5%。

（4）对含不同数量水平裂缝缺陷的混凝土三点弯曲梁试件进行测试，结果表明断裂韧度和断裂能随着裂缝缺陷数量的增加而降低，且裂缝数量由0 增加至3 时，失稳韧度降低约21.9%，断裂能降低约20.4%。

（5）裂缝缺陷长度、位置和数量对混凝土断裂测试结果具有显著影响，后续研究还需对裂缝缺陷的宽度、角度等参数作进一步分析。同时，针对含裂缝缺陷的楔入劈裂试件和紧凑拉伸试件的断裂测试结果需进一步进行试验研究分析。