基于RBF 代理模型和粒子群算法的水交换优化研究
戚 蓝,郑诗豪,,张丛林
(1.天津大学 水利工程仿真与安全国家重点实验室,天津 300072;2.中国科学院 科技战略咨询研究院,北京100910)
随着经济社会的发展,良好的水环境日益成为人民群众美好生活的重要需求,而良好的水交换,有助于改善海湾、港口、人工岛、湖泊等水域的水体质量和周边的生态环境。因此,开展水交换的研究、寻找提高水交换能力的措施和更加优化的换水方案,是十分必要的。目前的相关研究主要分以下两个方面:一是针对近岸海洋水域,如海湾、港口、人工岛等,已有研究选取水体交换周期[1]、半交换时间[2]、水体交换率[3]、纳潮量[4]等指标,定量分析研究区域内水交换的效果。且研究发现通过增加研究区域与外海的水交换通道,有助于增强水交换能力[5]。二是针对天然和人工湖泊,已有研究发现通过引水置换的工程措施,能显著改善西湖[6]、玄武湖[7]等湖泊的水环境,且引水水位差越大,水交换效果越好[8]。由此可见,引水置换是一种改善水环境的有效方法,且提高水位落差后水交换的效果明显。总体来看,已有研究取得了大量成果,但还有待进一步完善,主要体现在:一是目前研究中,通过增大引水差实现引水置换,从而改善水环境的方法实质是增大引水量,但对正常蓄水位固定(即引水量固定)的水域是否可行有待研究。二是已有研究大部分采用数值模拟[9-10]的方法开展研究,计算效率较低,且人为改变参数范围的局限性较大。
本文拟在已有研究的基础上,提出一种新的技术手段用以开展水交换优化研究,并以实际工程为例,验证本文所提方法在水交换优化研究方面的可行性和优越性。
1 研究方法
代理模型技术能够有效代替复杂的数值模拟分析,而智能算法可用于求解代理模型,在参数范围内寻找模型的最优解。因此,本文试图建立基于代理模型的水交换优化模型,通过智能算法寻优,从而求解出水交换的最优方案,并以某人工岛游艇别墅区港池初拟方案为例,对上述方法进行验证,从而得出最终结论。
1.1 RBF 代理模型
RBF 代理模型对于非线性复杂问题,泛化能力强、收敛速度快,是较为常用的代理模型。RBF 网络是单隐层的前向网络,由输入层、隐含层和输出层构成,隐层节点激活函数为径向基函数,包括高斯函数、反射Sigmoid 函数和逆多二次函数。如果RBF 神经网络输入训练样本为Xk时,网络第j 输出神经元的实际输出为[11]:

式中:x 为输入变量;y 为输出变量;N 为隐层神经元个数; ω为权重系数; Ø(r)为径向函数;r 为待测点x 与数据中心 ci之间的欧氏距离。
1.2 粒子群算法
常用的智能优化算法如遗传算法、粒子群算法、模拟退火算法、神经网络算法等,可用于求代理模型的最优解。其中粒子群算法运行速度快,实现性好,广泛应用于水利工程优化问题。高学平等[12]运用粒子群算法,成功求解相邻梯级泵站调水最优方案;郭玉雪等[13]等通过粒子群算法,求解梯级水库联合防洪补偿调度模型,从而拟定了梯级水库联合补偿调度原则。
粒子群算法通过模拟鸟类的觅食过程,完成问题优化过程。在该算法中,粒子在每一次迭代中通过跟踪两个“极值”完成更新:(1)个体极值(pb),粒子本身找到的最优解;(2)全局极值(gb),全种群目前找到的最优解。粒子i 将按照式(2)、(3)更新自己的速度和位置:

式中: vi(t) 为第i 个粒子在t 时刻的速度; xi(t)为第i 个粒子在t 时刻的位置;c1,c2为学习因子,通常取2;r1,r2为[0,1]上随机数;ω 为惯性因子。
1.3 数值模拟
MIKE21 是由丹麦水利学研究所(DHI)开发的平面二维数学模型,用于模拟河湖、海湾及海洋波浪、泥沙等。模型是基于三向不可压缩和Reynolds 值均布的Navier-Stokes 方程,并服从于Boussinesq 假定和静水压力的假定,二维非恒定浅水方程组为:

动量方程为:
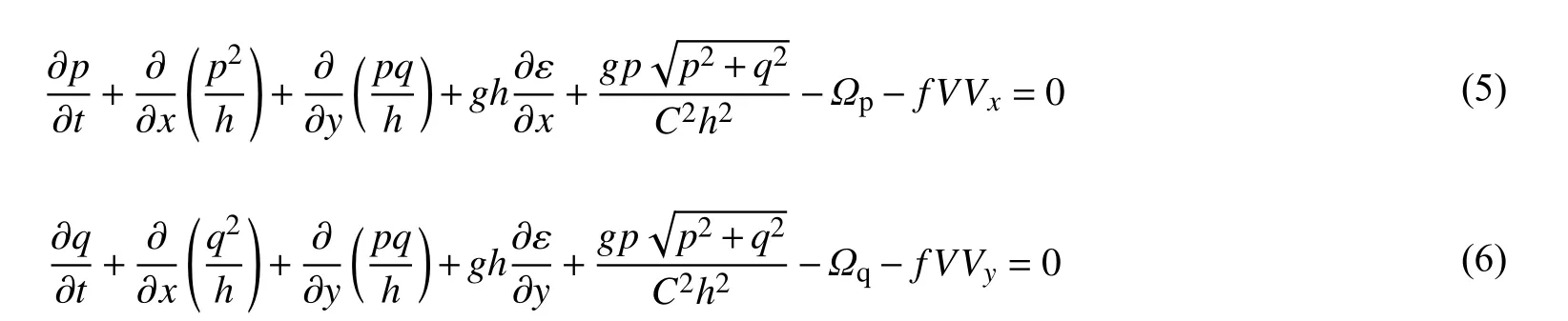
对流扩散方程为:
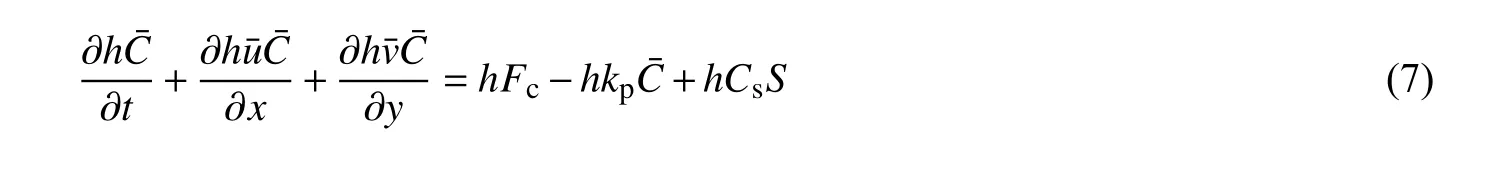
其中水平扩散项表示为:

采用溶解性保守物质A 作为示踪剂,不考虑物质A 的降解、絮沉等其他因素,仅考虑物质A 的对流扩散作用,以反映研究区域内的水交换程度。假定研究区域内原有水体中物质A 的初始含量为100%,引入海水使研究区域内水位上升,外海中物质A 的含量为0,新旧水体发生掺混,通过水体内物质A 的含量变化,从而反映出水交换的程度。
2 算例验证
2.1 研究区域
研究区域为某人工岛南端的游艇别墅区港池。该人工岛呈双鱼环抱圆形,半径840 m,规划面积2.2 km2,其中填海形成陆域面积1.8 km2,形成岸线11.7 km。该岛由东、西两个半岛及中心岛组成,由北向南设置一条内河道,游艇别墅区港池位于该岛西南方向。内河道南端布置双线船闸,闸室有效长度23 m,闸室有效宽度8 m,两侧边墩宽6.5 m,中墩宽12 m。具体布置见图1。游艇别墅区港池低水位1.0 m,正常蓄水位2.5 m,通过船闸与外海进行水交换。初拟换水方案为当外海水位上升至1.0 m 时打开船闸引水,当水位上升至2.5 m 时关闭闸门,使港池内水位和外海水位同步上升。本次研究依据外海潮位资料,改变船闸闸门开启时间,从而获取不同的引水落差。
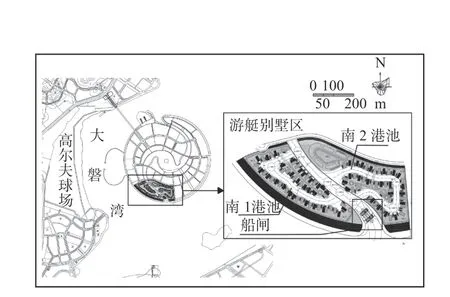
图1 人工岛和游艇别墅区示意Fig.1 Artificial island and yacht villa area
2.2 样本选取与计算
合理选取引水方案样本,利用MIKE21 水动力和对流扩散模型计算每个样本,样本结果用于建立和验证基于RBF 代理模型的水交换优化模型。
2.2.1 样本选取 根据外海潮位资料,影响引水方案的两个重要参数为开闸门的时刻和引水时长,开闸时间范围为13:00 至15:00,引水时长范围为0~120 min。主要考虑引水结束时港池内平均水位能否达到正常蓄水位2.5 m、平均污染物浓度能否明显下降且在港池内分布均匀。如果输入变量数为x,则构建RBF 代理模型至少需要2x+1 个样本[12]。在此基础上,本文按照初选样本、构建RBF 代理模型、增加样本优化模型的顺序,最终以10 min 为开闸门时间间隔,引水时长以20 min 叠加,并且在水位变化快的位置增设样本点,共选取46 个样本方案。其中训练样本和测试样本按照7∶3 的比例随机划分,共包含33 个训练样本和13 个测试样本。
2.2.2 数学模型及网格划分 根据人工岛地形资料,提取地形坐标和边界坐标,按1∶1 建立人工岛整体模型如图2 所示,共生成三角形网格9 338 个。在此基础上,从中提取出位于人工岛内河道南端的游艇别墅区港池的独立模型,并对独立模型网格进行加密如图3 所示,共生成三角形网格6 939 个。

图2 人工岛整体模型Fig.2 Artificial island overall model

图3 港池独立模型Fig.3 Harbor independent model
2.2.3 边界条件 人工岛整体模型和港池独立模型的开边界均指定为水位过程,由于工程所在区域为缓流区,涨潮平均流速为0.38~0.46 m/s,落潮平均流速为0.32~0.34 m/s,潮流动力较弱,因此可忽略潮流对内外水交换的影响,仅考虑由水位差产生的水流动力。引水时边界水位变化过程根据平均高潮位潮型设定,潮位资料见表1[14],其他边界均设置为陆地边界。

表1 潮位资料Tab.1 Tidal level data
2.2.4 数学模型验证 由于缺少游艇别墅区港池的实测资料,参考已有研究,利用人工岛物理模型试验6 个点位的实测流速资料[15],验证人工岛整体数学模型。由于游艇别墅区港池独立模型是从整体模型中提取而得,因此可间接对游艇别墅区港池独立模型进行验证。人工岛内河道对称布置6 个测点如图4所示,利用各测点物理试验得到的最大流速,与数值模拟结果进行比较(见表2)。为了评价模型的性能,本文采用由Wilmott 提出的统计学方法[3]对数学模型的实效性进行评价,该方法计算式如下:

式中:Ea为实测值与计算值之间的偏差;M 为模拟值;D 为实测值;为实测平均值;N 为样本个数。该评价指标中Ea的值位于[0.65,1.00]时表示数学模型精度极好。经计算,各测点数值模拟最大流速与实测值吻合较好,Ea=0.995 说明该模型对人工岛内河道水动力模拟情况良好,游艇别墅区港池独立模型可以用于本研究中样本的计算。
2.3 模型参数设置
RBF 网络输入变量为开闸时间和引水时长,而输出变量为引水结束后港池内平均水位。本研究由于样本数量有限,且为了尽可能得到最佳逼近值,故采用正则化RBF 网络,其网络隐层节点数等于输入的样本数,并将所有输入的样本设为径向基函数的中心,各径向基函数取统一的扩展常数。函数选用高斯函数,该函数具有形式简单、径向对称、光滑性好等优点[16],表达式为:

图4 测点布置Fig.4 Measuring point
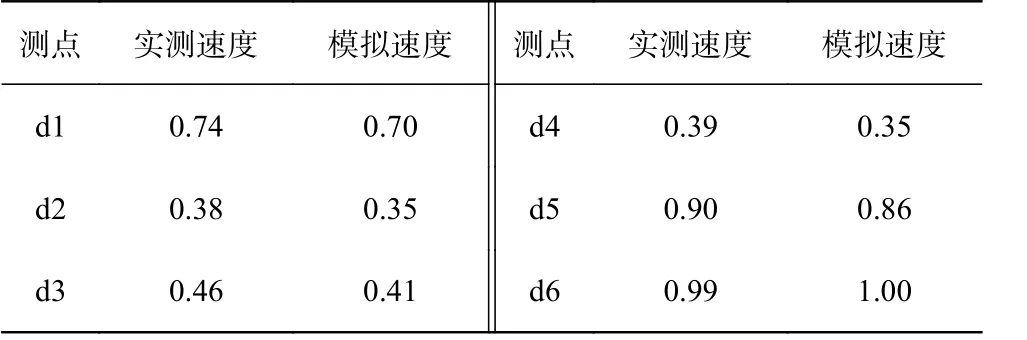
表2 人工岛内河道各测点最大流速统计Tab.2 Maximum flow rate statistics of various measuring points in rivers in artificial islands 单位:m/s

式中:r 为待测点x 与数据中心 ci之间的欧氏距离; σ为扩展常数,其取值与样本数量和散布特性有关,本文令其等于基函数中心与样本集输入模式之间的平均距离[16]。
2.4 粒子群算法参数设置
不同引水方案的最终目的相同,即引水结束后港池内平均水位为2.5 m,因此粒子群算法的寻优目标为求模型输出值与2.5 之间差值绝对值的最小值,故设置适应度函数见式(11)。而在样本计算时发现,在引水结束后港池内平均水位达到2.5 m 这一条件下,引水时长越短,港池内新旧水体之间掺混效率越高,水交换越显著。因此,约束条件为引水时长最短。

式中:f 为适应度函数值;abs 为求(y −2.5)的绝对值;y 为基于RBF 代理模型的水交换优化模型的输出值。
利用粒子群算法求解基于RBF 代理模型的水交换优化模型,待优化变量为模型的输入值,即开闸门时间和引水时长,开闸时间参数范围为13:00—15:00,引水时长参数范围为0~120 min。参数包括最大迭代次数、粒子个数、惯性权重系数、学习因子,结合已有研究的参数设置[17-19],本文粒子群算法的参数设置分别为:最大迭代次数100,粒子个数50,惯性权重0.9,学习因子c1和c2均取2。
3 结果分析
3.1 样本计算结果
基于MIKE21,利用水动力和对流扩散模型,分别计算46 个样本方案下,对应的引水结束时港池内平均水位,最高、最低水位和引水结束后污染物平均浓度。由于在计算样本时发现,在引水结束后的46 h 内,新旧水体掺混较为剧烈,港池内不同位置的污染物浓度变化较快,而在46 h 后水交换趋缓,因此选取引水结束后46 h 污染物平均浓度作为样本的一个输出指标。样本计算结果见表3。
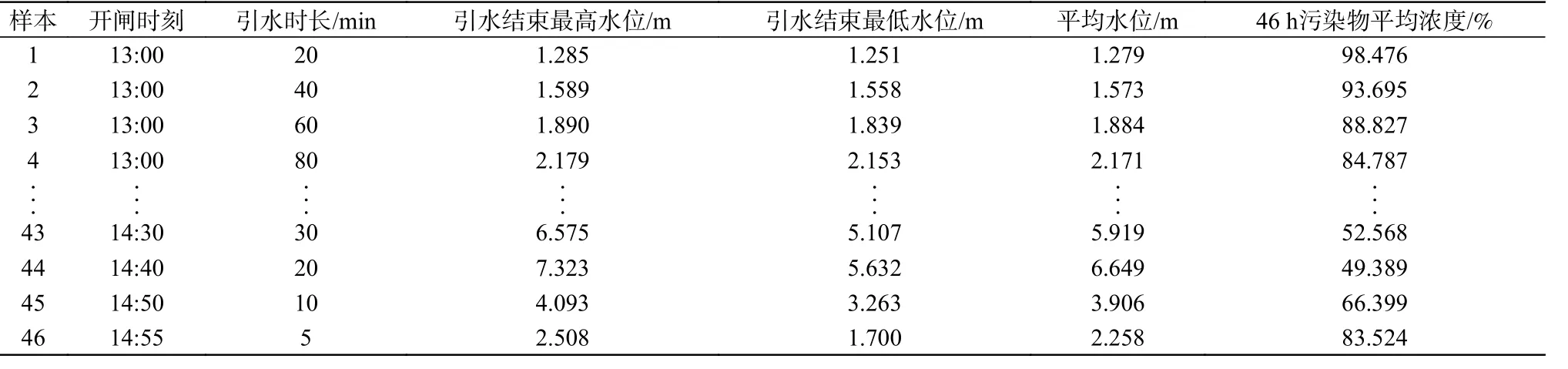
表3 引水方案样本及数值模拟结果Tab.3 Water diversion scheme and numerical simulation results
为消除不同数据之间量纲不同的影响,提高RBF 代理模型的计算精度,需要将RBF 代理模型的输入参数(闸门开启时间、引水时长)和输出参数(引水结束后港池内平均水位)3 个指标进行数据归一化处理,归一化到[−1,1]区间内。
3.2 水交换优化模型构建结果
基于RBF 代理模型,建立不同引水方案下开闸时间和引水时长与引水结束后港池内平均水位的响应关系。17 次迭代的均方误差达到0.000 9<0.001 0。而测试集平均水位与预测结果的相关性分析如图5 所示,预测值与真实值的R2为0.956 99,说明二者之间相关性较好,证明基于RBF 代理模型的水交换优化模型精度较高。
在基于RBF 代理模型的水交换优化模型成功构建后,RBF 代理模型一次抽样所需的时间量级为秒,而利用MIKE21 计算一个样本所需时间约3~4 h。相较传统的数值模拟方法,基于RBF 代理模型的水交换优化模型大大提高了计算效率。
3.3 粒子群算法优化结果
本文基于RBF 代理模型建立不同引水方案与最终港池水位的响应关系,利用粒子群算法,在RBF 代理模型输入参数的取值范围内寻找适应度函数的最小值,最优适应度值变化曲线见图6,最终得到适应度函数最小值为0.000 3。此时对应的RBF 代理模型输出值为2.500 3 m,输入参数为14:54开闸门,引水时长362 s。将此方案代入水动力和对流扩散模型计算,得到该方案下引水结束后港池内平均水位为2.495 2 m,平均水位相对误差为0.20%,说明基于RBF 代理模型的水交换优化模型精度较高,可以寻找到引水方案参数范围内的最优方案。
该研究区域初始引水方案为在潮位上升至1.0 m时打开闸门引水,潮位上升至2.5 m 时关闭闸门(即样本6),游艇别墅区港池水位和外海水位同步上升,引水时长120 min。而通过本文所提方法得到的最优方案引水时长仅需362 s,大大提高了水交换的效率。如图7 和8所示,最初方案引水结束46 h 后,南1、南2 两个港池内不同位置的污染物浓度仍很不均匀,尤其是南1 港池的西北拐角处、南2 港池靠近内河道位置的水体污染物浓度依旧接近100%,说明上述位置的水体还未和新引进水体发生交换,水交换的效率较差。而在最优方案下,引水结束后经过46 h,新旧水体掺混效率更高。南1、南2 两个港池内各个位置的污染物分布均匀,经过1 次引水浓度基本已经下降至70%,水体更新更为显著。
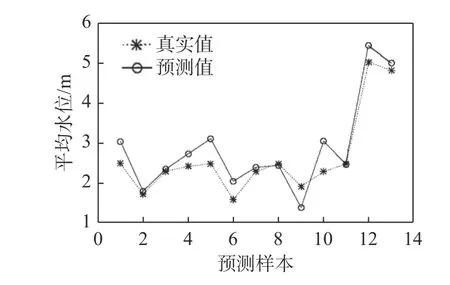
图5 测试集平均水位与预测结果相关性分析Fig.5 Correlation analysis between average water level in test set and prediction results

图6 每代最优适应度值变化曲线Fig.6 Optimal fitness value curve for each

图7 初始方案引水结束46 h 污染物浓度Fig.7 Concentration of pollutants after the initial water diversion scheme for 46 h

图8 最优方案引水结束46 h 污染物浓度Fig.8 Concentration of pollutants after the optimal water diversion scheme for 46 h
4 结 语
仅靠传统的数值模拟方法开展水交换研究,难以获取最佳水交换方案,且计算成本高、耗时长。本文提出基于RBF 代理模型和粒子群算法的水交换优化方法,并以某人工岛游艇别墅区港池初拟方案为研究对象,验证该方法的可行性和优越性。
(1)为构建基于RBF 代理模型的水交换优化模型,首先根据资料确定参数区间,选取46 个方案样本,利用MIKE21 水动力和对流扩散模型,对每个样本进行数值模拟计算;然后用选定的46 个样本,构建并验证基于RBF 代理模型的水交换优化模型;最后采用粒子群算法对基于RBF 代理模型的水交换优化模型求解,得到最优换水方案。
(2)利用上述方案研究某人工岛游艇别墅区,构建的基于RBF 代理模型水交换优化模型的预测值与真实值之间的R2=0.956 99,相关性较强;通过粒子群算法得到最优引水方案,将该方案代入水动力和对流扩散模型进行求解,与粒子群算法求解RBF 代理模型结果进行比较,相对误差为0.20%。证明模型精度高,且通过粒子群算法能获取参数区间范围内的最优方案。
(3)基于RBF 代理模型的水交换优化模型1 次计算所需时间量级为秒,而传统的数值模拟方法1 次计算所需时间量级为小时,证明基于RBF 代理模型的水交换优化模型计算效率较高。

