新型超高压爆破片安全泄放装置的结构设计及密封性能研究

杨 超,惠 虎,顾雪铭,黄 淞,周忠强

(1.华东理工大学 机械与动力工程学院，上海 200237；2.上海华理安全装备有限公司，上海 201108)

0 引言

伴随着现代化工业和科学技术水平的持续进步，压力容器行业的设计、制造水平得到了突飞猛进的发展。近几年，压力容器不断朝着极端化、高参数化、轻量化和大型化的方向发展，其中超高压容器的应用日趋广泛，它是聚乙烯生产、食品高压加工、人造水晶等行业不可或缺的关键设备，因此，超高压容器已逐渐被当做一门综合性很强的专业学科[1-3]。

根据超高压容器自身的特点，其内部的工作压力较高，当设备发生紧急情况时，容器内部的压力和温度变化时间很短，为防止其发生超压爆炸，需要在反应装置中安装超高压爆破片安全泄放装置。因此，超高压爆破片安全泄放装置作为超高压容器的最后一道安全屏障，起着至关重要的作用。爆破片安全泄放装置是一种由爆破片和夹持器等零部件组成的非重闭式压力泄放装置，在设定爆破温度下，爆破片两侧压力差达到预定值时，爆破片即刻动作[4]。爆破片安全泄放装置发展至今已有近百年历史，国内外学者对爆破片开展了大量的理论与试验研究。

(1)爆破片变形几何关系的研究。

Gleyzal[5]利用几何关系和物理方程，推导出爆破片发生变形过程中径向应变和周向应变理论公式的雏形；Weil等[6]在Gleyzal的基础上，考虑大应变对变形的影响，采用自然对数法得到双向应变的计算公式；Timoshenko等[7]借助板壳理论，验证了对数应变的几何公式。但是，上述研究都是在小变形的基础上得到的，而爆破片结构的变形属于大变形范畴，因此，Lake等[8-10]利用体积不变法、弧长法和弧线轨迹法，推导出等效应力和等效应变的计算公式。

(2)爆破片设计爆破压力的研究。

高光藩[11]从薄膜曲率和壁厚对极顶处应力的影响出发，提出了一种计算设计爆破压力的半经验公式；金巨年[12]通过试验发现，半经验公式中的抗拉强度和系数的选取都要通过试验获得；王军等[13]假设材料的强化规律为幂次强化，并考虑塑性大变形因素，对设计爆破压力的计算公式进行了修正；随后，傅建等[14-15]利用有限元数值模拟和试验的方法，进一步验证设计爆破压力的计算公式。

(3)温度对爆破片影响的研究。

吴泽炜等[16]提出爆破压力随温度的变化而变化，并推导出温度折减系数的计算公式；赵保頔等[17-18]通过开展大容积钢制无缝气瓶整体火烧工况的分析研究，得到不同爆破片泄放装置在火烧环境下的响应规律。

(4)爆破片不同的结构对爆破性能影响的研究。

胡兆吉等[19-21]对正拱形刻槽爆破片、平板环向开缝型爆破片和双爆破片结构的爆破性能开展了性能试验及理论研究工作。

综上所述，前人虽然对爆破片开展了各种各样的研究工作，但都是对基于薄膜理论的中、低压爆破片提出的，对于厚径比大于1/30～1/20的超高压爆破片，国内外学者对其研究很少，对其整体结构的设计更少。本文针对超高压爆破片安全泄放装置，提出新型的设计结构，并通过数值模拟和试验的方法，验证新结构密封性能及爆破性能的合理性和可靠性。

1 新型超高压爆破片安全泄放装置

GB 567.3—2012《爆破片安全装置 第3部分：分类及安装尺寸》[4]的范围中明确提出：本部分适用的爆破片安全装置中爆破片爆破压力不大于500 MPa，且不小于0.001 MPa。GB 567.3—2012中虽然将爆破片的设计爆破压力提高到100 MPa以上，但通过与相关爆破片厂家交流后得知，由于其密封性能和可靠程度无法保证，GB 567.3—2012中提到的爆破片与夹持器的结构类型无法满足100 MPa以上的超高压工况。因此，针对超高压容器的使用工况，国内开发了一种断裂型安全泄放装置——爆破帽，这种帽式爆破装置的优点是爆破帽破裂后，泄爆通过面积大，泄放物料的阻力小，缺点是爆破帽的机械加工与测量都比较困难，为了回收帽顶，防止其伤及周边人员，需要一个较大的锻件，不仅安装不便，而且加工也比较费时。

本文提出的3种新型超高压爆破片安全泄放装置(分体式、焊接式、悬浮式)可以避免上述缺点。

1.1 分体式超高压爆破片安全泄放装置

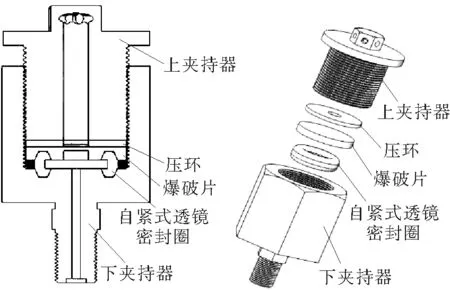
分体式超高压爆破片安全泄放装置是由上夹持器、压环、爆破片、自紧式透镜密封圈和下夹持器组成，如图1所示。

分体式超高压爆破片安全泄放装置的结构主要有如下设计特点。

(1)超高压爆破片安全泄放装置内部的连接方式参考ASME B1.1—2003《Unified Inch Screw Threads》，分别将上、下夹持器设计为UN A/B螺纹，通过UN螺纹将爆破片、压环和自紧式透镜密封圈进行相互配合，不仅能满足超高压工况下的剪切强度要求，而且安装方便。

(2)在自紧式透镜密封圈的内侧开设密封槽，利用密封圈圆弧的线密封和密封槽的自紧型式来确保超高压爆破片安全泄放装置的密封性能。

(3)在爆破片承压的一侧开设梯形沟槽，当爆破片与自紧式透镜密封圈相互配合时，不仅可以起到很好的密封作用，还可避免爆破片在承受超高压的工况下发生抽边现象而影响设计爆破压力的准确性。

(4)上部的夹持器开设放散孔，这样不仅可以满足容器安全泄放量的要求，还可以将爆破片爆破后产生的意外碎片收集到放散孔中，避免伤及周边人员。

1.2 焊接式超高压爆破片安全泄放装置

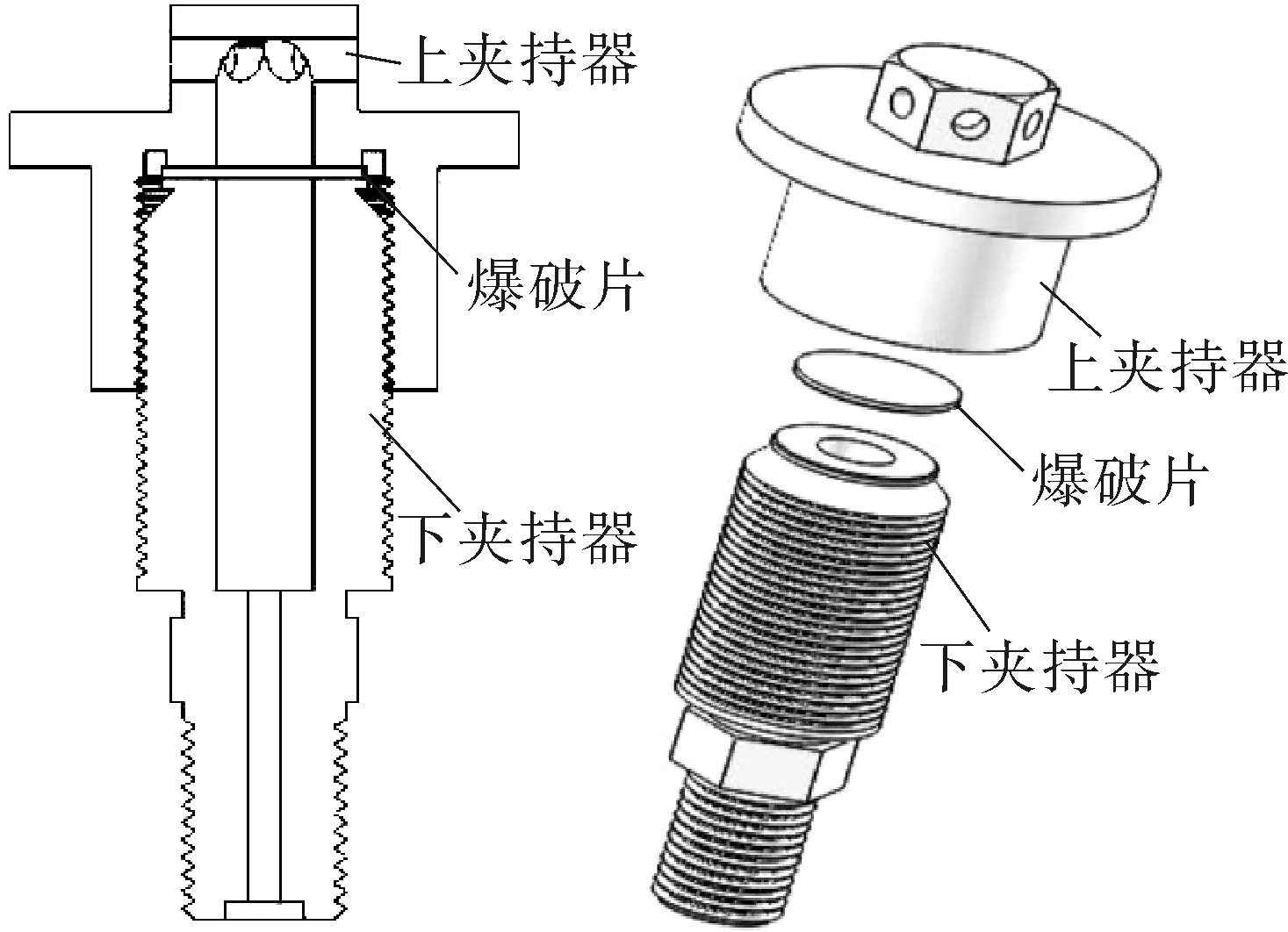
焊接式超高压爆破片是由上夹持器、爆破片和下夹持器组成，如图2所示。

(a)结构图 (b)实物图

(a)结构图 (b)实物图图1 分体式超高压爆破片安全泄放装置

(a)结构图 (b)实物图图3 悬浮式超高压爆破片安全泄放装置

焊接式超高压爆破片安全泄放装置的结构主要有如下设计特点。

(1)为避免焊接过程中产生的热量影响爆破片的爆破性能，因此将爆破片与下夹持器采用特殊方式进行焊接,不仅能够确保焊接强度，而且还能确保不改变爆破片的爆破性能。

(2)为达到节能减耗的目的，当爆破片爆破后，将下夹持器与爆破片焊接的部分切割掉，再将新爆破片与下夹持器进行焊接后可继续使用，这对于节约能源和降低成本具有十分重要的意义。

(3)此结构适用于各种超高压容器的结构尺寸，安装方便，不仅可以采用螺纹连接，而且还可以采用法兰连接，方便可靠。

1.3 悬浮式超高压爆破片安全泄放装置

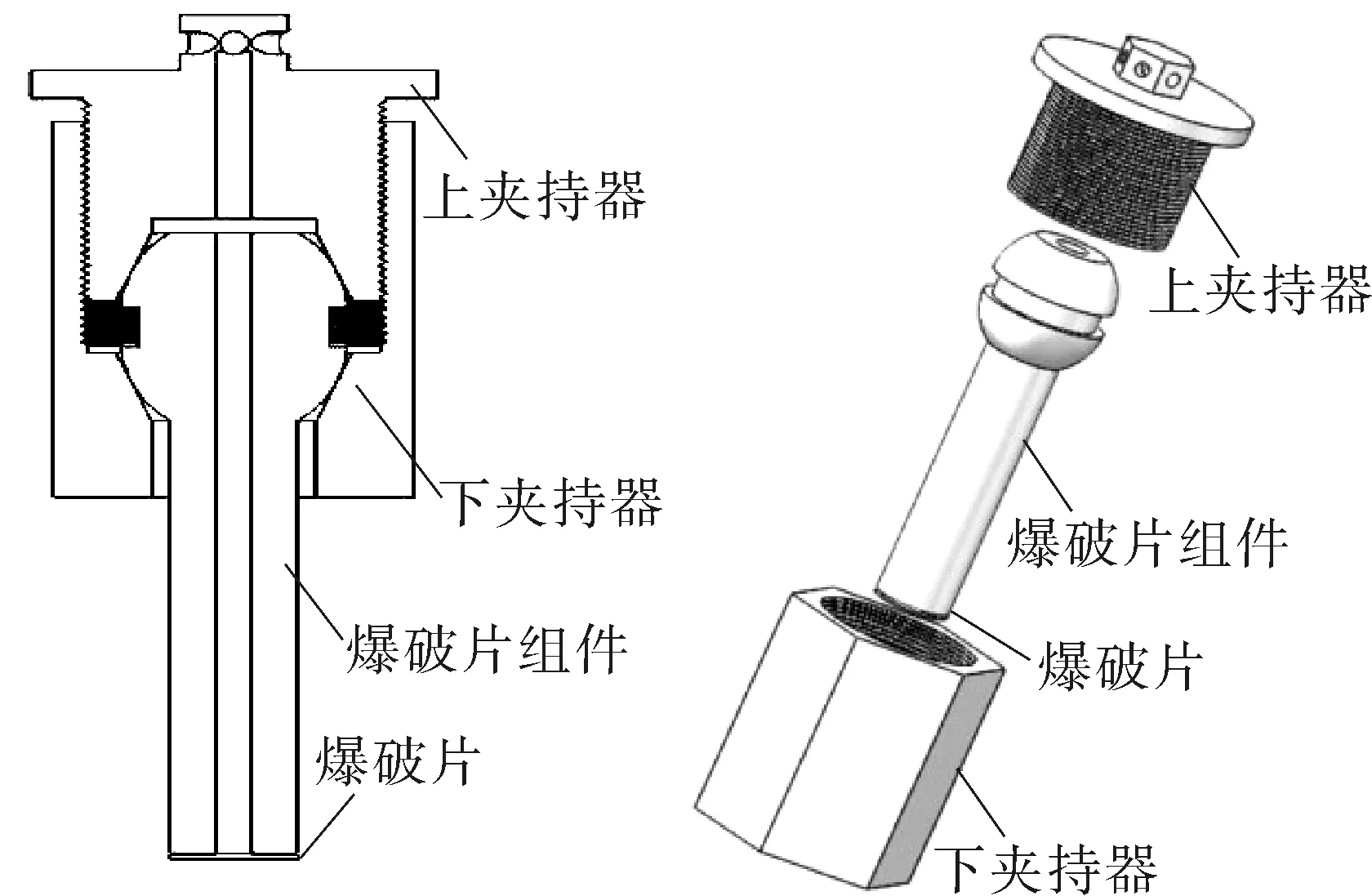
悬浮式超高压爆破片是由上夹持器、爆破片、爆破片组件和下夹持器组成，如图3所示。

悬浮式超高压爆破片安全泄放装置的结构主要有如下设计特点。

(1)自紧式透镜密封圈和泄放管道设计为一体式，然后将爆破片与其底部采用特殊方式进行焊接,形成爆破片组件，此结构不仅能够起到很好的密封作用，而且还能保持良好的爆破性能。

(2)当爆破片安全泄放装置与超高压容器进行连接时，将爆破片组件的下半部分沉入超高压容器，悬浮在容器内部，这样不仅避免由于外力作用破坏安全泄放装置的外伸部分，而且还节省容器外部的空间。

(3)为达到节能减耗的目的，当爆破片爆破后，将爆破片组件与爆破片焊接的部分切割掉，再将新爆破片与爆破片组件进行焊接后可继续使用，这对于节约能源和降低成本同样具有十分重要的意义，如图4所示。

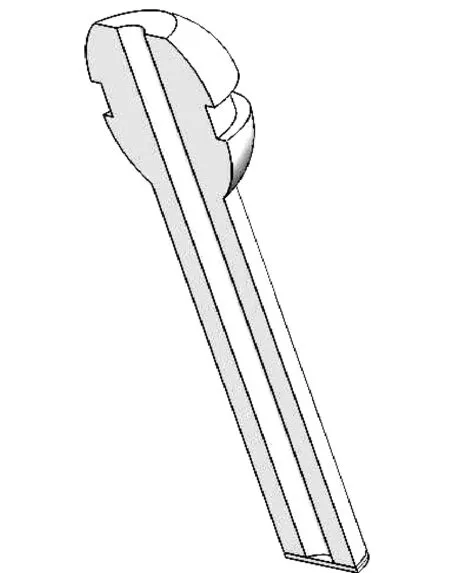
图4 爆破片组件和爆破片组焊剖面

(4)此结构适用于各种超高压容器的结构尺寸，安装方便，不仅可以采用螺纹连接，而且还可以采用法兰或焊接连接，方便可靠。

2 爆破片安全泄放装置密封结构的理论及数值分析

由于超高压容器的操作条件复杂，除了容器内部压力极高外，其压力、温度的波动变化，都将给超高压爆破片安全泄放装置的密封设计带来极大的考验，密封结构作为超高压爆破片安全泄放装置一个重要的组成部分，其结构强度及密封性能决定了超高压容器能否正常工作。以试验的方法验证超高压爆破片安全泄放装置的密封性能是最直观的做法，但考虑到超高压爆破片的爆破压力过高、危险性较大，在不能准确预测超高压爆破片密封结构的密封性能及结构强度可靠的前提下，无法随意开展超高压爆破片密封性能的试验工作。随着电子计算机的快速发展、普及，以及有效的大型ANSYS有限元分析软件的问世，可采用理论研究与有限元数值分析相结合的方法获得超高压爆破片密封结构的结构强度及密封性能，可大大节省人力和财力，在理论计算结果较为成熟的基础上开展后续的试验工作，是确保试验顺利进行，以及设备和人员安全的基础保障。由于焊接式爆破片安全泄放装置的密封性能安全可靠，本节可不考虑，分体式和悬浮式爆破片安全泄放装置均采用自紧式透镜密封圈的型式进行密封，由于分析方法一致，因此本节对分体式爆破片安全泄放装置的自紧式透镜密封圈的密封性能进行重点讨论。

2.1 密封结构壁厚的确定

自紧式透镜密封环厚度的确定是密封结构的前提条件，若厚度较薄，则初密封较好，但在较高的压力条件下，则会造成密封圈弯曲失效或强度破坏；若厚度较厚，则有可能影响初密封，因此，本节首先对自紧式透镜密封环厚度的确定展开研究。自紧式透镜密封圈的受力模型如图5所示，图中σz表示经向应力，σθ表示周向应力，σr表示径向应力。由于自紧式透镜密封圈径厚比较小，所以密封圈在工作过程中可看作两端有加强作用的厚壁圆筒，为三向应力状态。密封圈内任意点微元体承受内压载荷时的受力模型如图6所示。

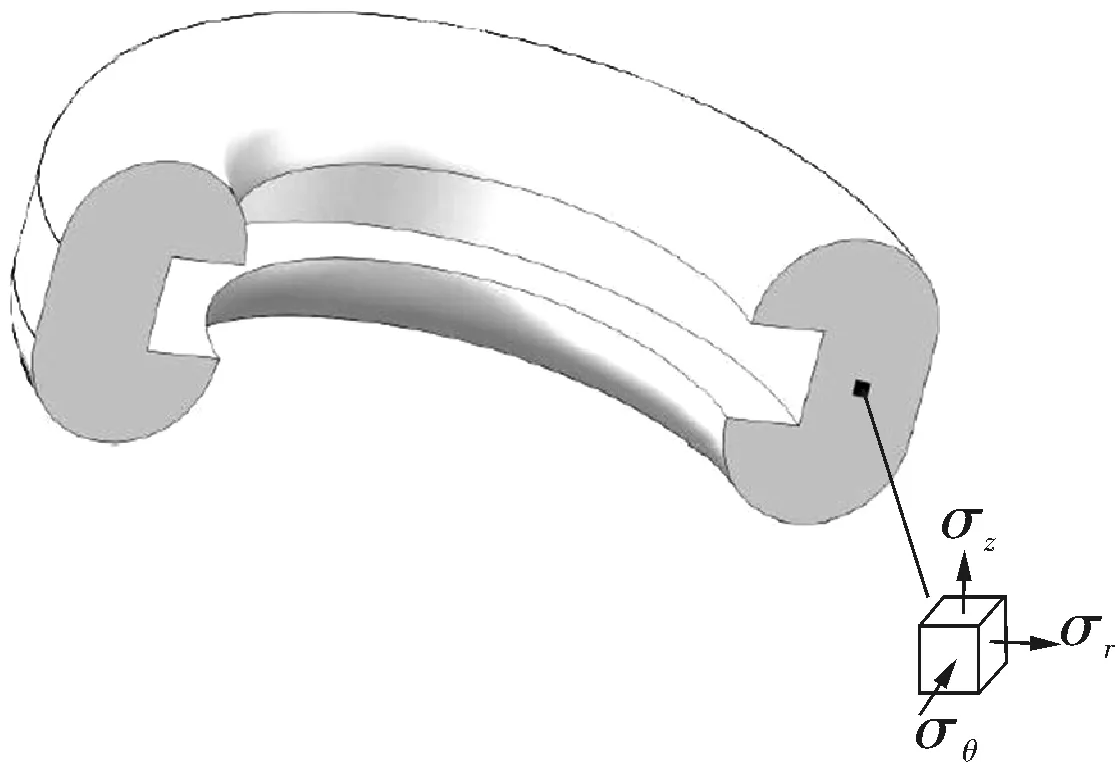
图5 密封圈模型

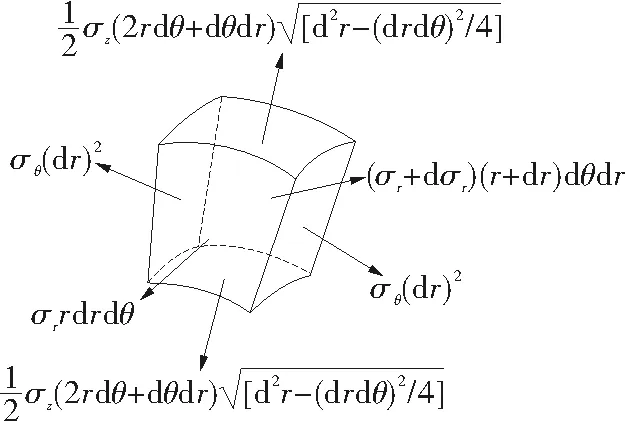
图6 微元体受力模型

根据微元体的受力状态，建立厚度方向的平衡方程：

(σr+dσr)(r+dr)drdθ-σrrdrdθ

(1)

式中r——介于密封圈内半径和外半径之间任一点的半径，mm。

对上式进行拆分，略去高阶无穷小及同类项，得到下式：

(2)

借助Mises屈服条件公式及拉美公式：

(3)

(4)

式中r1,r2——密封圈的内半径和外半径，mm；

P——内压，MPa。

可得到密封圈外缘壁厚的计算公式：

(5)

式中σy——材料实际测量得到的屈服强度，MPa。

2.2 密封结构数值模拟分析

2.2.1 材料特性试验

自紧式透镜密封圈在承压过程中，牵扯到双重非线性问题——几何非线性和材料非线性。对于材料非线性，从试样局部产生塑性屈服开始，材料的应力-应变关系就不属于线弹性本构方程，必须采用非线性的弹塑性本构关系。针对材料的非线性，在ANSYS前处理模块中选用多线性等向强化模型，在输入材料弹性模量和泊松比的同时，还要录入材料的真应力-应变曲线。材料的真应力-应变曲线可通过式(6)获得，且如图7所示。

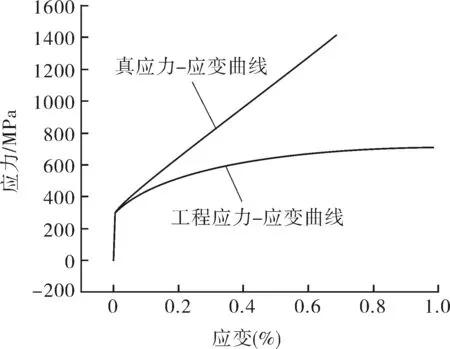
图7 材料本构关系

εt=ln(1+ε)σt=σ(1+ε)

(6)

2.2.2 非线性力学分析模型

自紧式透镜密封圈为轴对称结构，另外，密封结构的边界条件如接触状态、介质压力、约束等也符合轴对称条件，因此将有限元分析的三维模型简化为二维轴对称模型，如图8所示。在划分单元网格时，采用二维四节点实体单元Plane 182，在接触单元的选择上，由于上、下夹持器刚度比密封圈的刚度大很多，属于典型的刚体-柔体接触类型，因此分别选择Targe 169和Conta 172单元进行模拟。

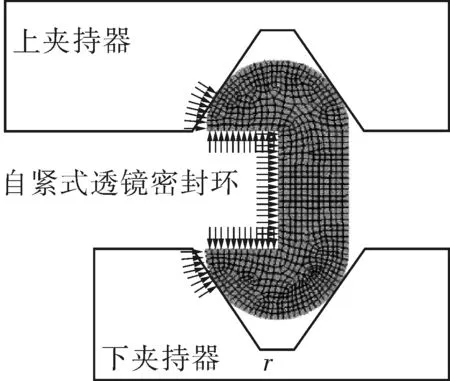
图8 数值模拟模型

在形成密封的过程中，自紧式透镜密封圈与上、下夹持器的接触区域采用拉格朗日乘子法，此算法作为独立的自由度进行计算，避免了穿透位移带来的误差，并且也无需定义接触刚度，能够很好的避免穿透问题带来的计算误差。在设计过程中对自紧式透镜密封圈表面的粗糙度指标要求在0.6 μm以下，要求较高，因此摩擦系数取0.1，为避免计算过程中造成太多的迭代次数或不收敛，计算允许穿透的系数取0.1。

2.2.3 载荷边界条件

在整个模拟过程中，为防止夹持器发生移动和旋转，限制上夹持器的所有自由度；为模拟夹持器对爆破片的夹紧力，给定爆破片下夹持器沿Y方向的位移为0；由于采用部分建模方式进行模拟，因此对爆破片的边缘施加对称载荷。同时，对自紧式透镜密封圈的内侧施加对应的压力载荷。

2.2.4 结构强度的研究分析

本节根据式(5)得到直径为34 mm，承受的介质压力分别为100,150,200,250 MPa下所对应的密封圈壁厚，其尺寸分别为5,9,12,16 mm，并对其建模进行数值模拟分析，由于篇幅有限，本节展示出了其中4个模拟结果，如图9所示。

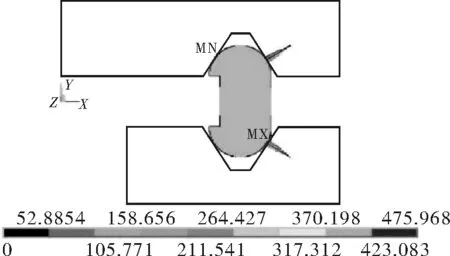
自紧式透镜密封圈的应力分析根据第四强度理论，运用Mises等效应力进行分析，结果表明：应力水平最高的位置出现在密封圈与上、下夹持器接触的部位，如图9(a)(c)所示，其对应的最大应力分别为370,524 MPa。如图9(b)(d)所示，材料首先在密封结构与上、下夹持器的接触区，以及密封槽内的应力集中区域进入屈服阶段，此后随着外载荷的增大，塑性区域向外扩展，但大部分材料仍处在弹性阶段，说明密封圈整体未进入塑性状态，其强度完全能够承受对应的介质压力，甚至更高的载荷水平。因此，可验证按照式(5)得到的自紧式透镜密封圈的壁厚能够满足强度要求。

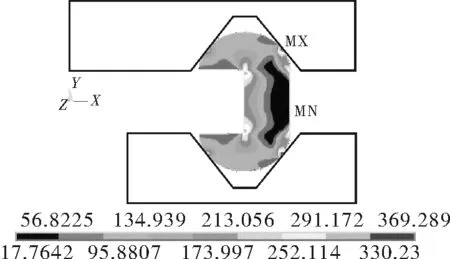
(a)应力云图(P=100 MPa)

2.2.5 密封性能的研究分析。

本节将研究自紧式透镜密封圈内密封槽的宽度和高度对密封面上最大接触压力的影响，以及密封面上的最大接触压力与介质压力之间的关系，如图10所示。由于密封圈上的接触压力与夹持器上的接触压力为作用力与反作用力，因此，本文在使用时均表示密封圈与夹持器接触面上的接触压力，并且是密封圈内侧面上的接触压力。

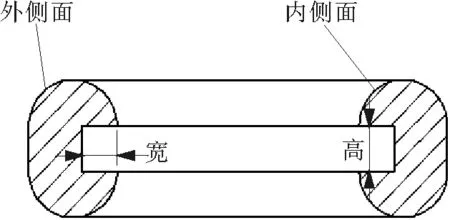
图10 密封槽的结构

(1)密封失效的判断准则。

在ANSYS中，需要采用密封失效准则来判断密封效果的好坏，其中密封失效准则包括挤出量判据、最大剪切应力判据和最大接触压力判据。挤出量判据是针对非金属材料而言，由于自紧式透镜密封圈为金属材料，在承压过程中密封圈材料不会被挤入密封间隙中，因此挤出量判据不适用于本密封结构。另外，本文重点对密封圈的自紧结构进行研究，暂不考虑材料的抗剪切能力，而最大接触压力判据可以更直观地反映密封面上的接触压力与介质压力之间的关系，以此对比密封性能的好坏，因此选择最大接触压力判据作为自紧式透镜密封圈密封效果的判断依据。最大接触压力的判据表达式如下：

Pc>P

(7)

式中Pc——接触压力，MPa;

P——介质压力，MPa。

(2)接触压力随密封槽高度变化的关系。

本节根据上文得到的密封圈在分别承受100,150,200,250 MPa介质压力下的壁厚，取其密封槽的宽度与各自的壁厚相等，其密封槽的高度H在4～30 mm的范围内，每2 mm取一个值作为密封槽的高度，共设置了14个尺寸，并完成了相应的有限元分析。由于篇幅有限，本节示出了其中4个模拟结果(见图11)，用以展现在不同密封圈尺寸和介质压力条件下，其密封面上接触压力的分布。

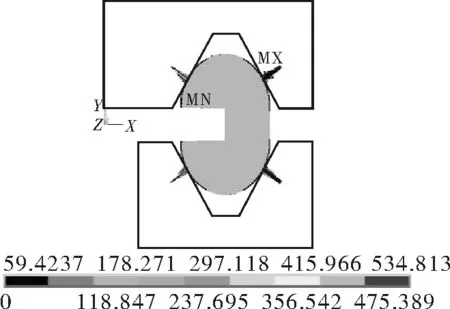
(a)P=150 MPa，H=6 mm

由图11可以看出，当介质压力分别为100,150,200,250 MPa时，自紧式透镜密封圈内侧与夹持器表面的接触压力均大于各自的介质压力，达到了自紧式密封的效果。

由图12可以看出，自紧式透镜密封圈密封槽高度的变化对接触压力没有太大的影响，随着密封槽高度的变化，其密封性能保持不变。但由图13可以看出，随着密封槽高度的变化，其Mises应力逐渐变大。因此，在确保加工精度的前提下，其密封槽的高度越小其应力水平越小。

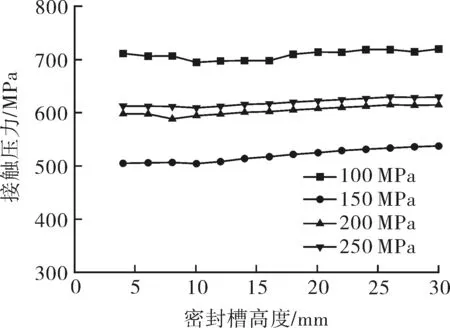
图12 接触压力随槽高的变化曲线

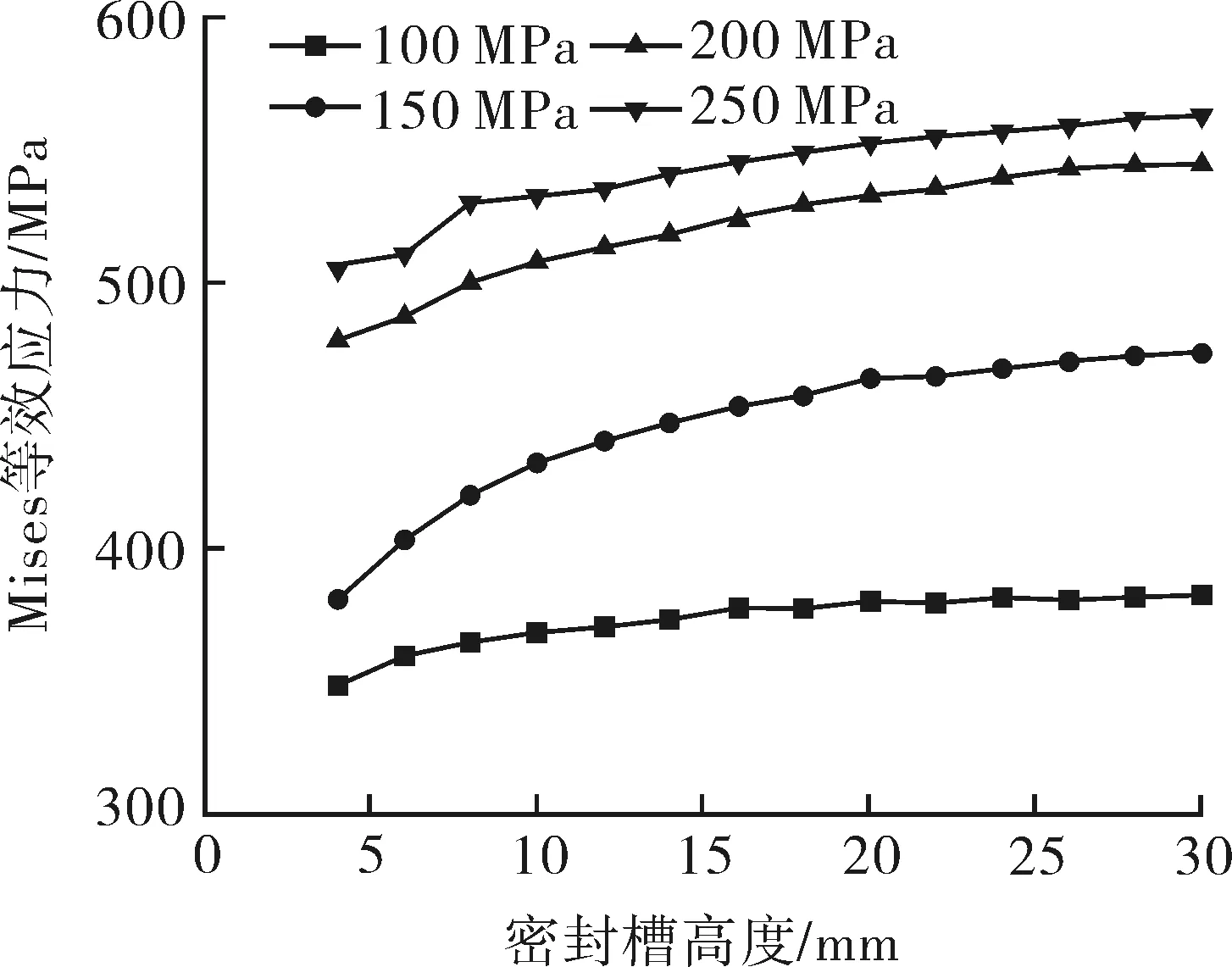
图13 Mises应力随槽高的变化曲线

(3)接触压力随密封槽宽度变化的关系。

在上文计算结果的基础上，设置介质压力在100,150,200,250 MPa下密封槽的高度分别为6,10,12,18 mm，其密封槽宽度W见表1。

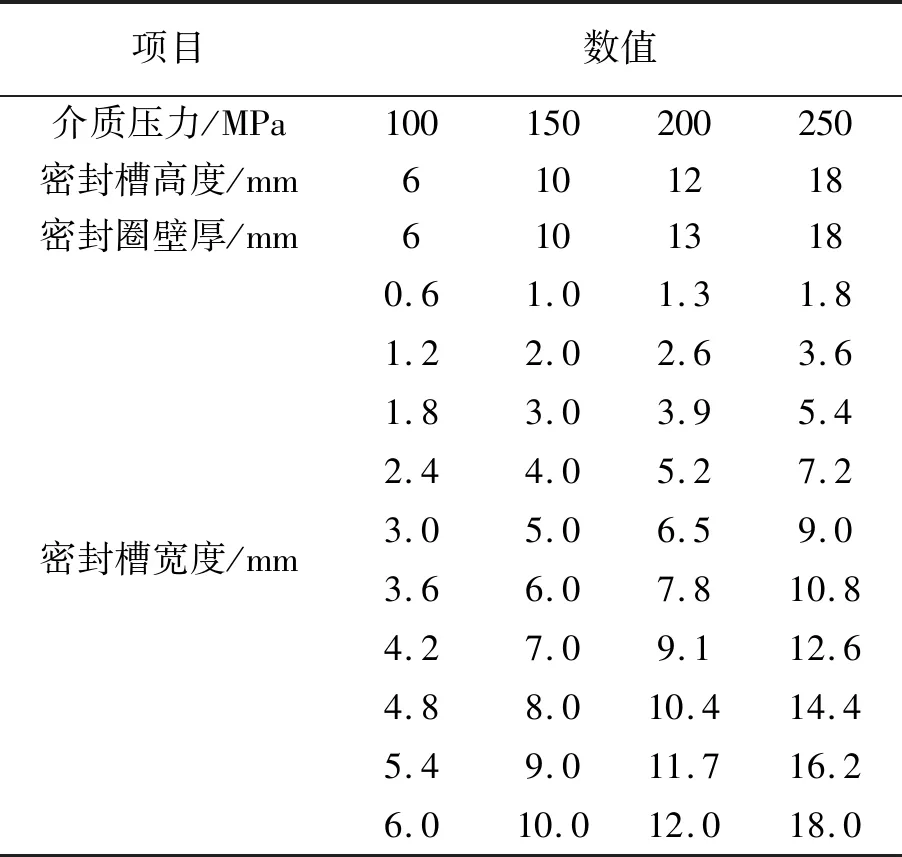
表1 自紧式透镜密封圈密封槽尺寸

由于篇幅有限，本节仅示出了介质压力在100 MPa时的4个模拟结果(见图14)，用以展现密封圈在不同密封宽度下，其密封面上接触压力的分布情况。

由图14(a)(b)可看出，介质压力定为100 MPa时，其内侧面上的接触压力均为0，虽然外侧面上的接触压力都在300 MPa以上，能够起到密封作用，但自紧式透镜密封圈内侧面上未起到任何自紧的效果。由图14(c)(d)可以看出，随着密封槽宽度的不断增加，密封圈内侧面上的接触压力呈现逐渐升高的趋势，说明密封圈的内侧面与夹持器表面随着压力的上升紧密压合，其接触压力均在300 MPa以上，自紧式透镜密封圈能够起到自紧的效果，并且其密封效果显著增加。接触压力随密封槽尺寸的变化曲线见图15。可以看出，接触压力与介质压力相等的点全都落在密封槽宽度与密封圈壁厚比值在0.60～0.65的范围内，说明当自紧式透镜密封圈密封槽的宽度与密封圈壁厚的比值取0.65以上的范围时，其接触压力将大于介质压力，自紧式透镜密封圈可以起到较好的自紧效果。

(a)W=1.2 mm

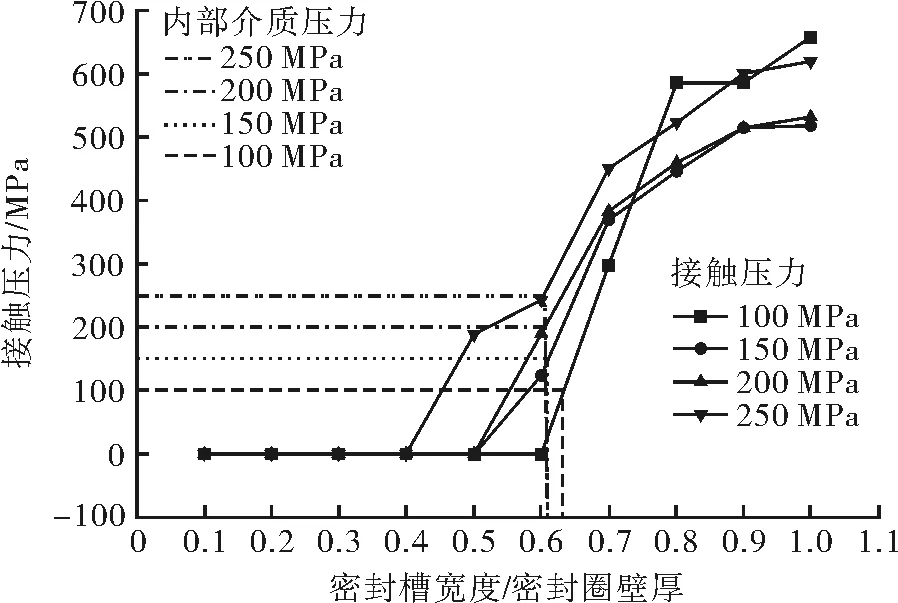
图15 接触压力随密封槽尺寸的变化曲线

3 超高压爆破片安全泄放装置的试验研究

由于悬浮式超高压爆破片安全泄放装置需要借助超高压容器才能开展试验工作，实验室条件有限，因此本节只针对分体式和焊接式超高压爆破片安全泄放装置开展相应的试验研究，验证新型超高压爆破片的密封性能和爆破性能。

3.1 实验平台的搭建

实验平台主要由Haskel气动增压泵、Autoclave高压阀、高压压力表、调压阀过滤器等部件组成，实验平台原理图如图16所示。

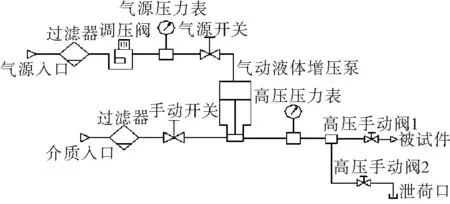
图16 实验平台原理

3.2 试件的制备

本文制备了分体式超高压爆破片安全泄放装置和焊接式爆破片安全泄放装置的试验试件，分别如图17,18所示。

图17 分体式爆破片安全泄放试件

图18 焊接式爆破片安全泄放试件

3.3 密封性能试验

将制备的分体式爆破片安全泄放装置的试件安装到试验系统中，对其开展密封性能试验工作，分别在50,100,150,200 MPa的介质压力下进行保压，保压一段时间，得到试验曲线如图19所示。

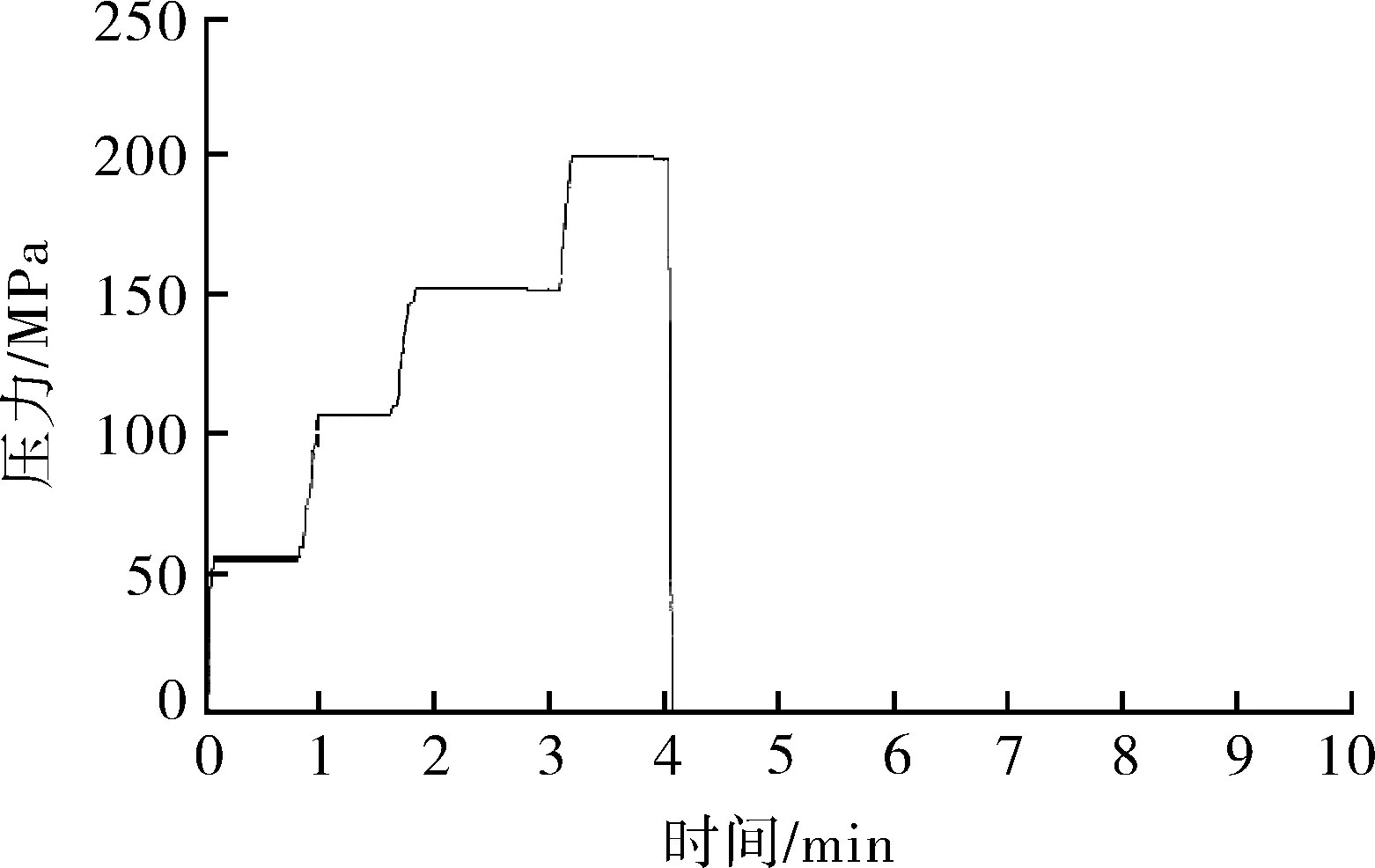
图19 保压试验曲线

通过上述试验可知，自紧式透镜密封圈在不同介质压力下的密封性能均良好，且强度可靠，未发生任何变形。

3.4 爆破性能试验

由于悬浮式爆破片安全泄放装置需借助超高压容器进行爆破试验，但目前的试验条件无法满足试验要求，因此本节只针对分体式和焊接式超高压爆破片安全泄放装置进行爆破试验，如图17，18所示。试验温度为常温，试验介质为水，试验结果如表2所示。根据试验结果可知，两种结构型式的爆破压力非常相近，均可满足正常超高压环境下的使用工况。

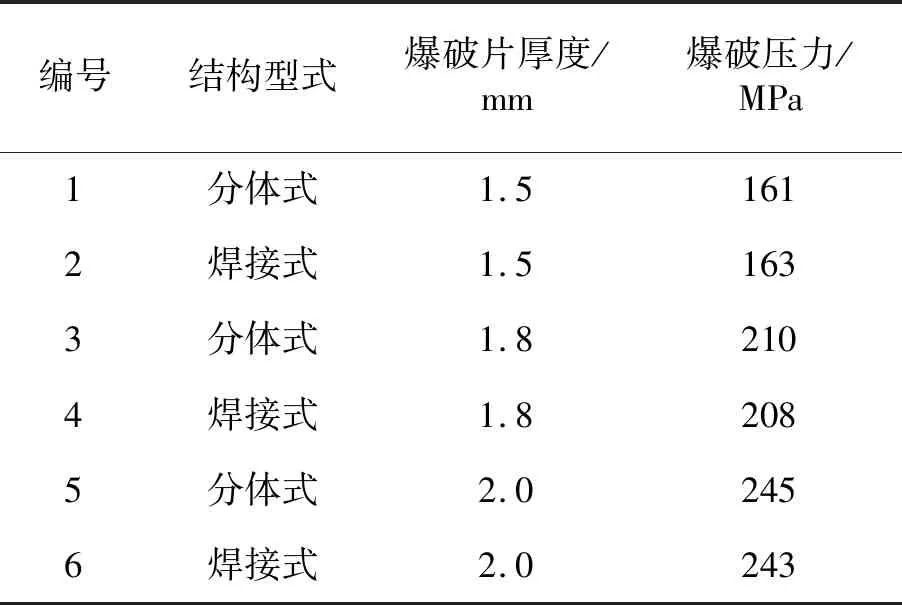
表2 超高压爆破片安全泄放装置爆破试验结果

爆破后的超高压爆破片如图20所示。出现此种破坏的原因是超高压爆破片安全泄放装置内没有放置带有圆角的压环，而是将爆破片直接与上夹持器直接接触，而上夹持器的内角为直角，因此爆破片与上夹持器内直角接触的区域为高应力集中区，从而出现剪切破坏。

(a)分体式焊破片 (b)焊接式爆破片

图20 试验后的超高压爆破片

4 结论

本文对超高压爆破片安全泄放装置的设计结构、密封性能及爆破性能进行分析研究，得到如下结论。

(1)提出了3种新型超高压爆破片安全泄放装置的设计结构：分体式、焊接式和悬浮式。

(2)借助Mises屈服理论和有力矩理论，得到了自紧式透镜密封圈壁厚的计算公式。

(3)利用ANSYS有限元数值模拟分析法，进一步验证了自紧式透镜密封圈在不同的介质压力下，其强度完全满足设计要求。

(4)利用ANSYS有限元数值模拟中的拉格朗日乘子算法，并借助最大接触压力的判断准则，得到了自紧式透镜密封圈密封槽尺寸的确定方法。

(5)搭建了超高压爆破片爆破实验平台，通过对分体式和焊接式超高压爆破片安全泄放装置开展的试验研究工作，不仅验证了自紧式透镜密封圈的强度和密封性能，还验证了超高压爆破片安全泄放装置新型结构的爆破性能。