考虑应力集中效应下钢带缠绕增强复合管爆破性能分析

陈 伟,唐夏焘,陈 长,陈兴阳,白 勇

(1.浙江省特种设备科学研究院,杭州 310020;2.浙江省特种设备安全检测技术研究重点实验室,杭州 310020;

0 引言

接头(管道连接器)作为整个管网主要组成部分，在管网系统中占有重要位置，但接头又是整个管网系统最薄弱的环节，理论上整个管网系统中接头的数量越少，则管道服役可靠性越高[1]。

目前，工业界和学术界对于管道接头的研究主要集中于分析接头在外载荷下的力学性能以及改进接头结构以满足特定工况要求。Zou等[2]分析了钢管用单搭接头在扭转载荷下的力学性能，通过不同理论构建了接头受力的力学模型，并将分析结构分别与试验数据对比，以选取最优模型。Cheng等[3-4]设计了一种内嵌压电陶瓷的智能接头，通过压电效应及逆压电效应，嵌入的压电陶瓷片可作为传感器和执行器来减轻接头内部的应力集中效应，该团队基于一阶剪应变原理建立了接头理论模型，并将分析结论与有限元数据对比，结果显示，改变压电陶瓷中的电场可有效优化接头内部剪应力的分布。Lees[5]通过试验，分析了玻璃纤维缠绕增强复合管的接头在内压和拉伸组合载荷下的力学性能，分析结果显示，接头最具代表性的工况是纯拉伸载荷下其性能变化趋势。Lotsberg[6]结合实际工况，分析了管网中多种结构在外载荷作用下的应力集中系数(Stress Concentration Factor,SCF)，包括因制造误差引起的平板对焊处的应力集中系数、不同外径的管道对焊处的应力集中系数、不同壁厚的管道对焊处(变径处)的应力集中系数，以及具有初始椭圆度的直缝焊接钢管在受到弯曲载荷作用时的应力集中系数。

钢带缠绕增强复合管内压测试显示，部分情形下爆破点在靠近接头的部位，在此情形下可认为接头所引起的应力集中效应影响了管道的整体变形状态。针对该情形，本文基于薄壁壳理论，推导内压载荷下靠近接头部位的管壁中增强层的位移-应变表达式，并分析应力集中效应对管道强度的影响。

1 管道接头结合处的应力集中系数

钢带缠绕增强复合管的结构主要包括内层高密度聚乙烯(HDPE)层(用于输送介质以及隔绝来自介质的腐蚀)、外层HDPE层(用于隔绝来自外部环境的冲击并保护中间增强层)、中间螺旋缠绕的钢带增强层。管道接头与接头之间通过螺栓法兰连接，接头与管道之间通过接头内外套筒之间带锯齿腔压紧管壁而形成稳固连接，其结构如图1所示。

图1 钢带缠绕增强复合管扣压式接头结构示意

文献[7]采用经典弹性力学模型分析钢带管在内压载荷下的力学性能，其描述的管道爆破试验中爆破点远离接头，可认为爆破处的管壁不受应力集中效应的影响，试验数据与经典弹性力学模型分析结果较为吻合。Lotsberg[6]分析了带有加强环的单层钢质管在内压载荷作用下的破坏形式，该破坏形式考虑了加强环处的径向位移不连续所造成的应力集中效应。

本文分析对象为带有扣压式接头的管道，对管壁中应力集中系数的定义方式为：(1)确定在达到爆破压力时远离接头端的管壁中钢带层因管壁膨胀引起的主轴应力σ1，该区域中管壁的变形均匀，无需考虑应力集中效应的影响；(2)确定在爆破压力下靠近接头端管壁中钢带层中因管壁膨胀引起的主轴应力σ2。则应力集中系数定义为：

(1)

2 钢带层等效压力

在复合管的整体径厚比偏大时，增强层中的单层钢带才能被当成薄壁壳结构。对于受到内压P的复合管，钢带层所承担的等效内压需重新计算。对于6层结构的钢带缠绕增强复合管，其中第k层内外表面的压力分布如图2所示。则该层增强层中与Lotsberg[6]计算单层钢质管中内压对应的等效压力表达式见式(2)，由该层的径向力平衡条件可得到式(3)。

p=σk-1-σk

(2)

(3)

式中t——第k层的平均厚度，mm；

l——沿轴向固定长度，mm；

σθ——第k层环向应力，MPa。

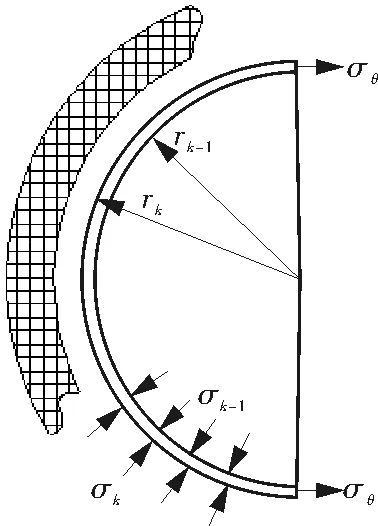
σk-1表示来自相邻内层对该层沿径向向外的挤压应力；σk表示来自相邻外层对该层沿径向向内的挤压应力[8]

图2 增强层内外表面压力分布示意

通过求解式(3),可求得p与σθ之间的关系：

(4)

式中k——管道截面层数，k=1～6。

式(4)即为某层增强层的钢带中等效内压的表达式，该式将被作为整体引入下文的分析中。

3 管壁位移-应变关系

假设接头为不可发生变形的刚性结构，接头在管道端部将管道六自由度全部约束而形成类似固支约束的边界条件。根据薄壁壳理论，管壁在内压载荷下的径向变形公式[9]为：

(5)

其中：

式中D——管壁中钢带的抗弯刚度,N/m，

υxθ,υθx——x-θ,θ-x方向泊松比；

w——管壁挠度，即管壁径向变形量。

对于某一段长度固定且两端带有扣压式接头的钢带缠绕复合管，如果其接头之间的有效长度l满足：l>2π/β，即可认为管道一端接头的约束导致管道在内压载荷下的形变不会影响到管道另一端接头对管道约束所造成的变形[10-12]，则管壁径向变形量表达式为：

(6)

在管道接头结合部建立笛卡尔坐标系，其中x沿管道轴向，y沿管道径向，如图3所示。假设管道体内不存在质量力且接头为刚性材料，则可认为靠近接头部分的管壁的径向位移为0[13-14]。

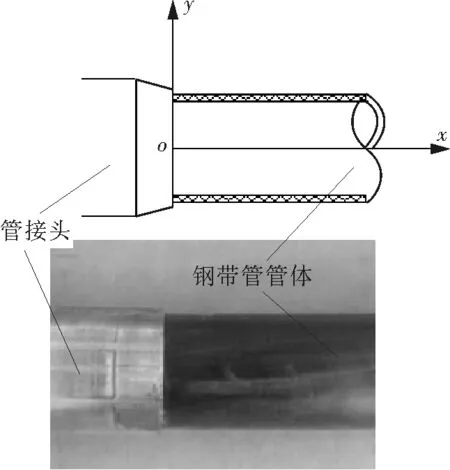
图3 管道端部笛卡尔坐标系

对于带有多层增强层的复合管，采用上节中推导的等效内压表达式(4)表示某单层增强层内表面压力，则考虑应力集中效应下管道第k层增强层环向应力与其径向位移之间的关系表达式为：

(7)

式(7)中，x和r分别为自变量，可知在该理论模型中管道增强层的径向位移不仅与该增强层的半径有关，亦和所考虑的点的轴向位置有关，即在内压载荷下钢带层径向位移会随轴向位置的变化而变化[15-16]。图4所示的算例表明，受内压载荷且端部全约束的管道其径向位移会沿轴向变化。在管道接头的结合处位移为0，随着x增大、管道的径向位移快速上升达到峰值，然后随着x增大、其径向位移又逐渐下降至平缓。位移峰值出现的位置靠近管道与接头的结合处。对于同种管材、不同载荷情形下，其径向位移亦不相同，压力越大、管道径向位移越大，且位移峰值的位移也略微不同[17]。

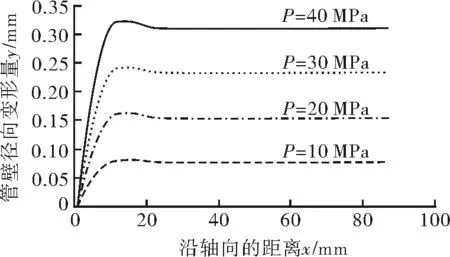
图4 不同内压载荷下管壁径向变形趋势

管道环向应变仅与其管道径向位移及管径有关，当管径确定后，管道环向应变与管道径向位移成正比。因此靠近接头部位的管壁，其环向应变也会存在峰值，该处应力最大，即为应力集中点。选取最内层增强层中钢带的主轴应力作为管道破坏的判据[18]，将式(7)中的变量r作为常量而仅考虑管壁变形沿轴向的变化，对式(7)求导并令其导数为0，求得位移最大点的位置。对式(7)赋值k=1并结合求导结果，可得到最内层增强层中钢带的最大径向位移ur(x)。假设管道的长度足够长，则可以认为在x趋于无穷处(远离接头处)的管壁的变形不受接头引起的应力集中效应影响，此处管壁位移规律服从文献[18]中描述的常规弹性力学模型。

算例中的管道半径为31 mm，管壁厚度为0.5 mm，管道长度假设为无限长对式(7)求极限，得到无穷远处管壁的径向位移表达式：

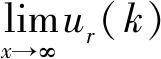
+sinβx)-1]

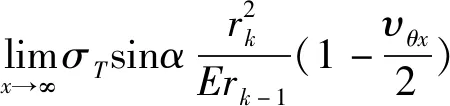
×[e-βx(cosβx+sinβx)-1]

(8)

式中σT——钢带沿缠绕方向的拉伸应力，即主轴应力。

不考虑应力集中效应的弹性力学解法,其假设管道沿轴向各点处的径向变形均匀连续，当最内层钢带中的环向应力到达强度极限后认为管道破坏，前期有很多关于采用此方法计算均质管、纤维增强复合管以及钢丝增强复合管的爆破应力的文献，且当爆破点位于远离接头部位时，计算值与试验值能较好符合。但是文献[18]中也提到考虑应力集中效应的管道的破坏形式是：爆破点靠近接头部位(如图5所示)。更精确而言，带有刚性扣压式接头的复合管在内压载荷下管壁的变形如图6所示。

图5 内压试验中管道的破坏点部位

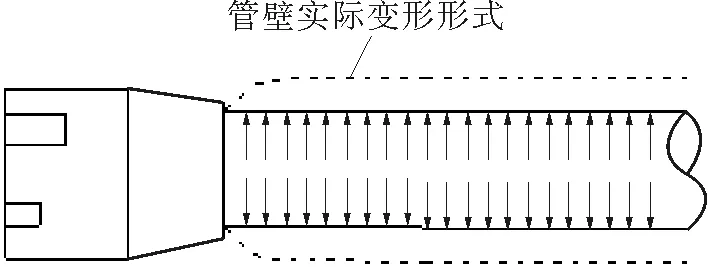
图6 加载内压后管壁变形示意

考虑到管壁的位移-应变的轴对称特性，结合式(8)，远离接头处管壁的环向应变表达式为：

(9)

式(9)揭示了考虑应力集中效应后管道的爆破压力与远离接头处管壁的应变之间的对应关系，由于远离接头处的管壁的径向位移-应变不受应力集中效应影响，可用式(9)替换经典弹性力学模型(不考虑应力集中模型)中的环向应变表达式，当σT逐渐趋近钢带的极限强度时，计算得到的内压值即为考虑应力集中效应下的管道爆破压力。

4 实例分析

4.1 实例分析1

算例1为2英寸(5.08 cm)4层增强层钢带管。采用本文提出的模型计算图5中所示管道的爆破压力，管道材料力学性能参数见表1，几何参数见表2。

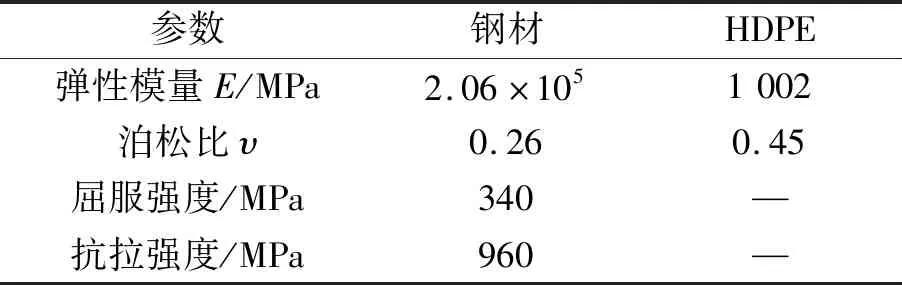
表1 管道材料力学性能参数

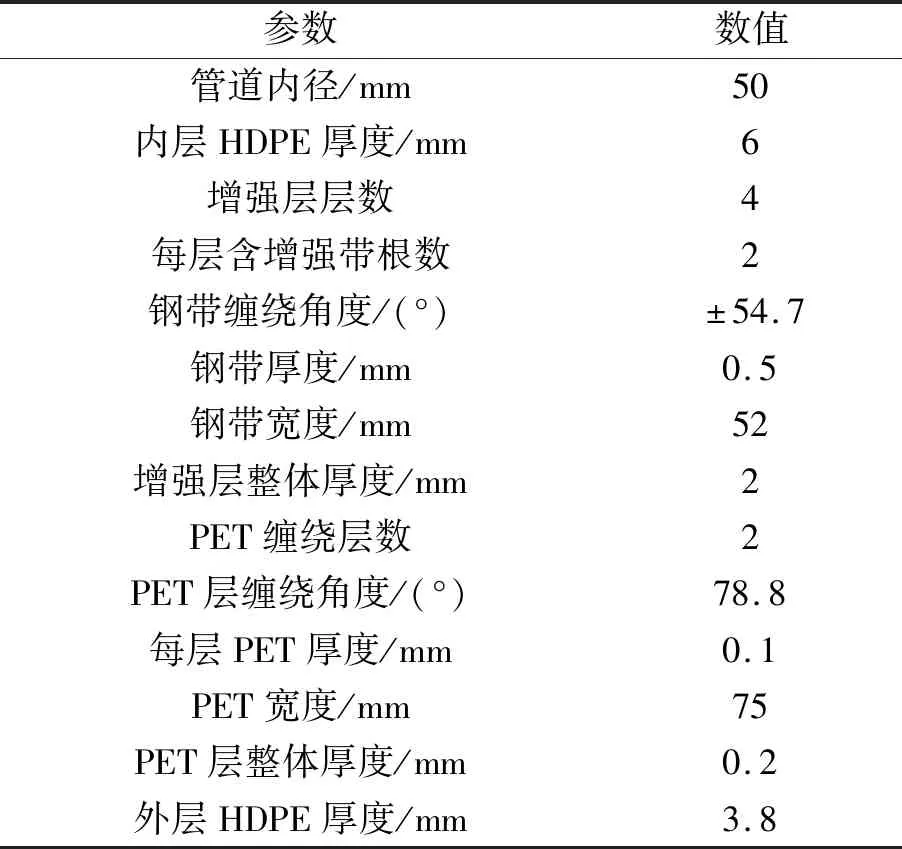
表2 2英寸(5.08 cm)4层增强层钢带缠绕增强复合管几何参数

试验过程中管道压力加载曲线如图7所示，可见管道爆破压力约为40.3 MPa。按照式(9)定义，当钢带主轴应力达到强度极限时管壁偏轴环向应变为0.002 826，偏轴环向应变-加载内压的关系如图8所示，则对应的计算所得爆破压力值为38.35 MPa。

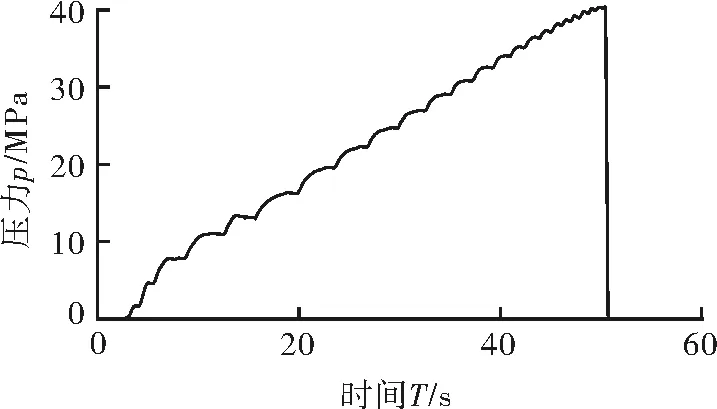
图7 2英寸(5.08 cm)4层增强层钢带管内压测试压力加载曲线

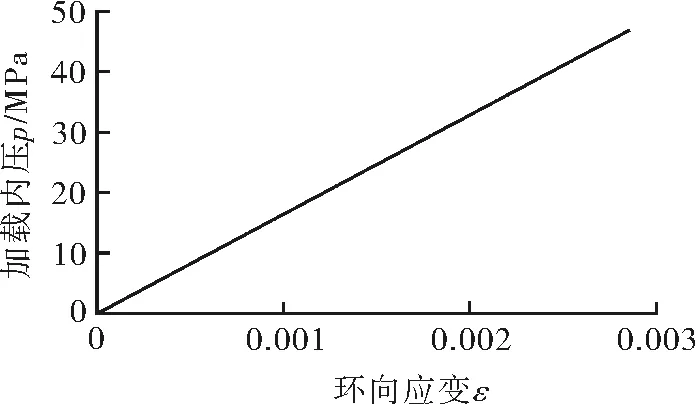
图8 加载内压-管壁环向应变关系曲线

表3列出了不考虑应力集中效应的经典弹性力学模型和考虑应力集中效应的模型所计算的管道爆破压力与试验爆破值的对比。可以看出，考虑应力集中效应之后，所计算的管道爆破值比试验值小约4.0%，结果偏保守；不考虑应力集中效应，计算爆破值比试验爆破压力的平均值大6.2%。

表3 考虑/不考虑应力集中效应情形下2英寸(5.08 cm)4层增强层管道爆破压力与试验值对比

本例中考虑应力集中效应时,靠近接头处钢带上的主轴应力为960 MPa，远离接头端管壁中不受应力集中效应影响的点的主轴应力为585.32 MPa，故应力集中系数为：

(10)

4.2 实例分析2

算例2为2英寸(5.08 cm)6层增强层钢带管,其力学性能参数见表1,几何参数与2英寸(5.08 cm)4层增强层钢带管几何参数(见表2)类似，不同之处在于其增强层为6层。试验过程中管道加压曲线见图9，爆破后管道及爆破点位置见图10。

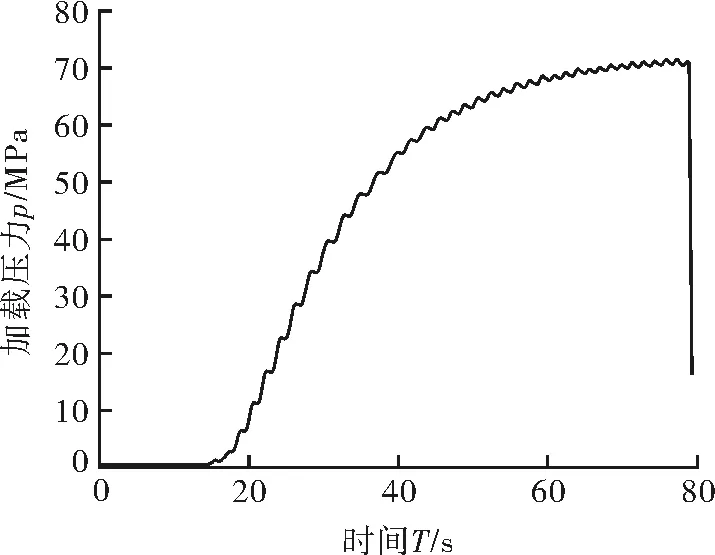
图9 2英寸(5.08 cm)6层增强层钢带管内压测试加载曲线

图10 2英寸(5.08 cm)6层增强层钢带管爆破位置

由图10可看出，爆破后管道中钢带断裂方向垂直于钢带缠绕方向，各增强层的扭矩不均使管道沿轴向扭转一定角度，从而导致外层HDPE的撕裂方向为斜切口。爆破点靠近接头位置，说明存在应力集中现象，接头的存在影响了管道的爆破压力。承受内压载荷的钢带增强层撕裂方向垂直于缠绕方向，外层HDPE亦被撕开，破口为基本垂直于管道轴向方向的斜切口。文献[19-20]中研究了超高压管式反应器端部结构的应力场分布，指出对于采用过盈配合的端部结构，其边缘存在较高的局部轴向拉应力。本文分析实例中扣压式接头通过外扣内挤的方式与管壁形成固定连接，其端部结构类似过盈配合。同时，由于管道中钢带的螺旋缠绕特性，受内压的管道具有强烈的轴向扭转趋势。在较高的局部轴向拉应力和轴向扭转趋势综合作用下，外层HDPE产生基本垂直于管道轴向方向的斜切口。分别采用经典弹性解法和考虑了应力集中效应的解法计算得到的管道爆破压力对比见表4。可以看出，对于受内压载荷的2英寸(5.08 cm)6层增强层钢带管，当爆破点在靠近接头部位时，采用不考虑应力集中的理论方法计算得到的爆破压力为78.46 MPa，比试验值70.56 MPa大11.2%；采用考虑应力集中效应解法得到的爆破压力为65.62 MPa，比试验值小7.0%。管道爆破时，不受应力集中效应影响区域的增强层上环向应力为501.18 MPa，则应力集中系数为：

表4 考虑/不考虑应力集中效应情形下2英寸(5.08 cm)6层增强层钢带管爆破压力与试验值对比

(11)

总体而言，采用经典弹性力学方法计算得到的管道爆破压力大于试验值；而考虑应力集中效应后计算的管道爆破压力小于试验值，结果偏保守。二者形成的压力区间可用于初步评估管道的抗内压性能。同时6层增强侧管道的应力集中系数大于4层增强层管道的应力集中系数，说明增强层的整体径厚比对管壁内的应力集中效应影响较显著，且径厚比越小、应力集中效应越明显。

5 结论

本文基于薄壁壳理论，分析了内压载荷下应力集中效应对管道强度的影响，并提出了一种考虑应力集中效应的管道爆破压力的计算模型，解释了管道爆破试验中爆破点靠近接头部位的原因。通过与经典弹性力学模型(不考虑应力集中效应)对比可知，在爆破点靠近接头的情形下采用该模型计算的钢带管的爆破压力值更接近试验爆破压力值，从而验证了该模型的适用性。得到结论如下。

(1)计算得到带有扣压式接头的2英寸(5.08 cm)4层增强层钢带管的应力集中系数为1.64；2英寸(5.08 cm)6层增强层钢带管的应力集中系数为1.92，说明带有扣压式接头的钢带管中应力集中效应会随着管道径厚比的减小而逐渐增大。

(2)通过该模型计算的管道爆破压力小于试验结果，而通过经典弹性力学模型计算的管道爆破压力大于试验结果，二者形成的压力值区间可为钢带管生产单位和施工单位初步评估其抗内压性能提供一定参考。