Gorenstein X-内射复形类的稳定性

于春艳，魏宝军，张文汇

(重庆师范大学涉外商贸学院 数学与计算机学院,重庆 合川 401520)

对C(R)中的任意复形

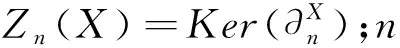
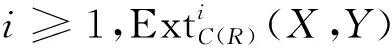
设A是R-模类(R-模的复形类)。称A是投射可解类,如果A包含投射模类(投射复形类),并且对A中任意正合序列0→X′→X→X″→0,若X″∈A,则X′∈A⟺X∈A。称A是内射解类,如果A包含内射模类(内射复形类),并且对A中任意正合序列0→X′→X→X″→0,若X′∈A,则X″∈A⟺X∈A。称Abel范畴中的序列L是HomC(R)(A,-)正合的，如果对任意A∈A,复形HomC(R)(Α,L)正合。

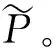
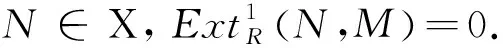
类似于内射复形的定义,我们首先引入X-内射复形的定义。

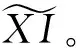
注记1(1)由[10,注记2.1.4]知内射模是X-内射模，但X-内射模不一定是内射模,因此结合定义1知内射复形是X-内射复形，但X-内射复形不一定是内射复形;

(2)X-内射复形类关于直积封闭;

(3)当X=Mod(R)时,X-内射复形即是内射复形;当X是有限表示复形类时,X-内射复形即是FP-内射复形(见文献[11,定义2.4])。

定义2[10]称R-模M是GorensteinX-内射模,如果存在R-模的正合序列

使得

(1)对任意i∈Z,Ii∈J;

(2)M≅Ker(f-1);

(3)对任意X-内射R-模G,序列HomR(G,)正合。

记GorensteinX-内射R-模类为GXI。

注记2(1)由[10,例2.5.2]知,内射R-模是GorensteinX-内射R-模;

(2)由[10,注记2.5.3]知,GorensteinX-内射R-模类关于直积封闭;

(3)由[10,定理2.5.7]知,GorensteinX-内射R-模类是内射可解类。

GorensteinX-内射复形的定义及性质

类似于Gorenstein内射复形的定义,我们给出GorensteinX-内射复形的定义。

定义3 称复形G是GorensteinX-内射复形,如果存在复形的正合序列

使得

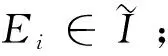
(2)G≅Ker(μ-1);

(3)对任意X-内射复形L,HomCR(L,E)正合。

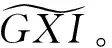
例1(1)每个内射复形是GorensteinX-内射复形.事实上存在复形的正合序列

…→I→I→…,

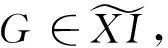
(2)一般地讲,GorensteinX-内射复形是Gorenstein内射复形。设G是GorensteinX-内射复形。由GorensteinX-内射复形的定义,存在内射复形的正合序列

…→G1→G0→G-1→G-2→…,

使得G≅Ker(G-1→G-2),并且对任意X-内射复形X,上述序列是HomC(R)(X,-)正合的。因为内射复形是X-内射复形,所以G是Gorenstein内射复形。例如,当X是有限表示模类时,由[8,注记2.2]知GorensteinFP-内射复形一定是Gorenstein内射复形。

注记3 若Ⅱ=…→I1→I0→I-1→I-2→…是内射复形的正合序列,并且对任意X-内射复形G,HomC(R)(G,Ⅱ)正合,则由对称性知序列Ⅱ中所有微分的象、核与余核都是GorensteinX-内射复形。

GorensteinX-内射复形类的一些基本性质。

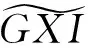
证明 由内射复形类关于直积封闭可得。

以下引理给出了任意复形是GorensteinX-内射复形的一个等价刻画。

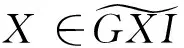
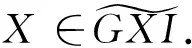
Ⅱ=…→I1→I0→I-1→I-2→…,

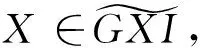
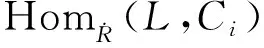
注意到存在(层次可裂的)正合序列

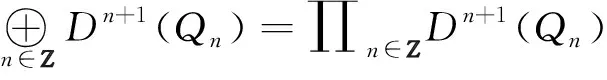
因为η是两个满同态的合成,所以η是满同态。因此有交换图

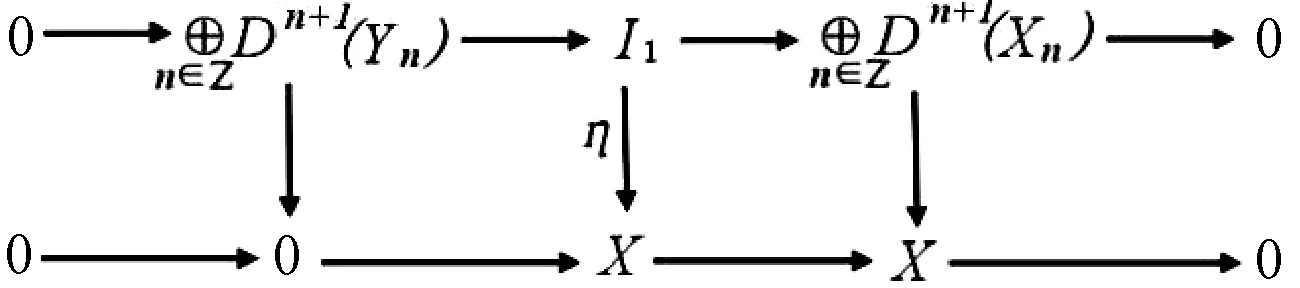
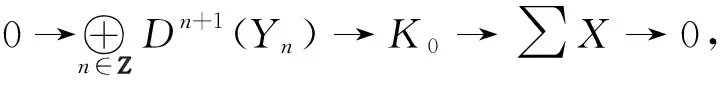
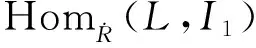
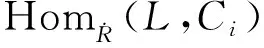
粘合,并且取d1=δη.

以下给出GorensteinX-内射复形的一些基本性质。

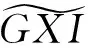
0→HomR(Lt+n,X)→HomR(Lt+n,Y)→

HomR(Lt+n,Z)→0,

进而有复形的正合序列

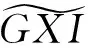
由以上结论可知,GorensteinX-内射复形类具有和Gorenstein内射复形类相似的一些性质。接下来,我们再研究GorensteinX-内射复形类的稳定性。

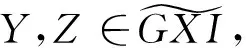
证明 ⟹显然。

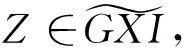
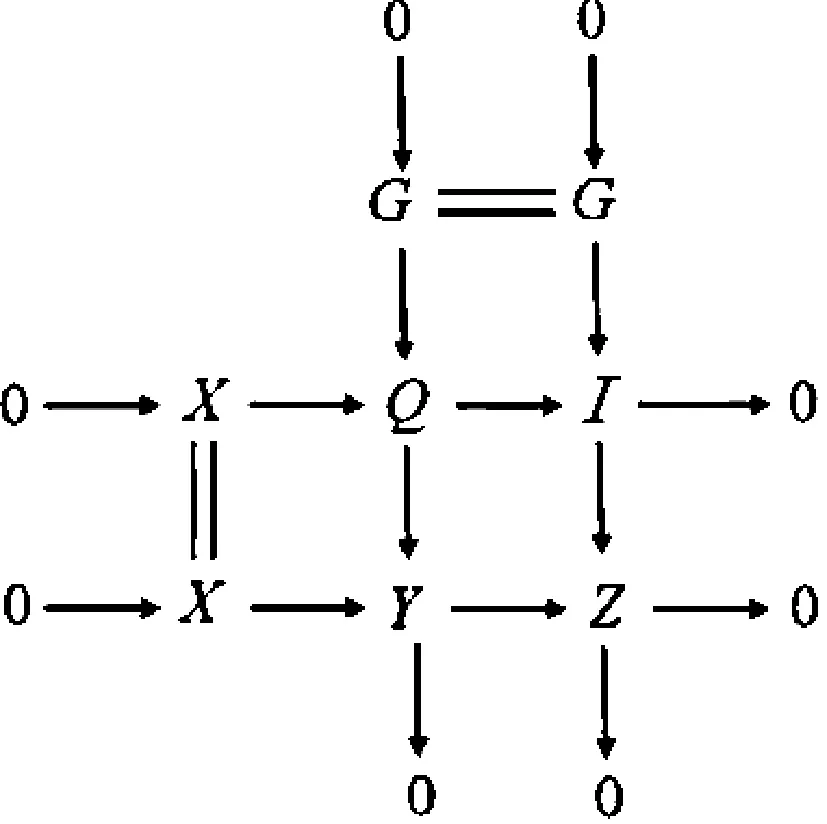
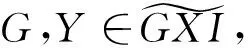
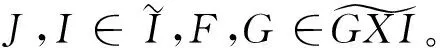
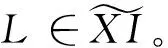
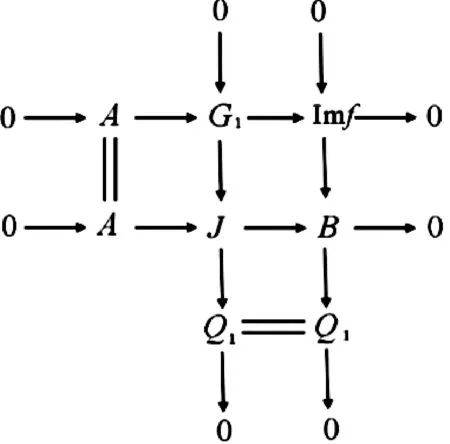
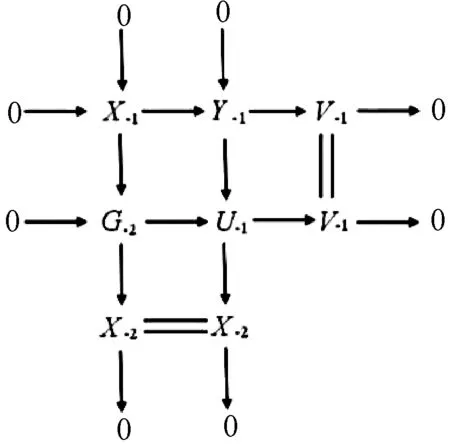
由第三列和正合序列0→Imf→G0→X→0知,有下列推出图：

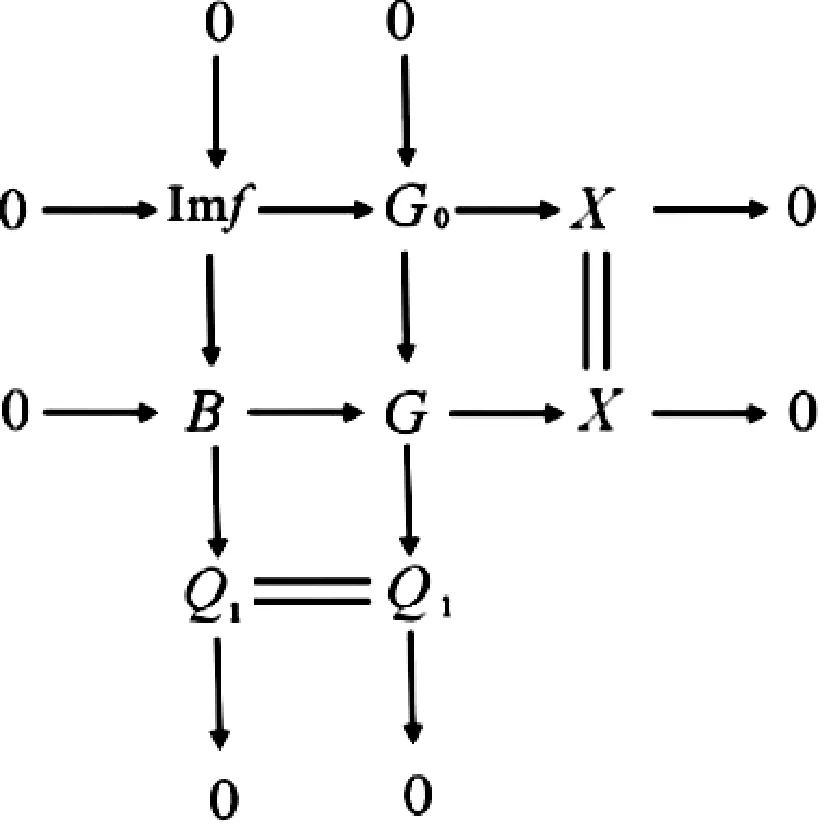
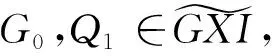
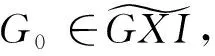
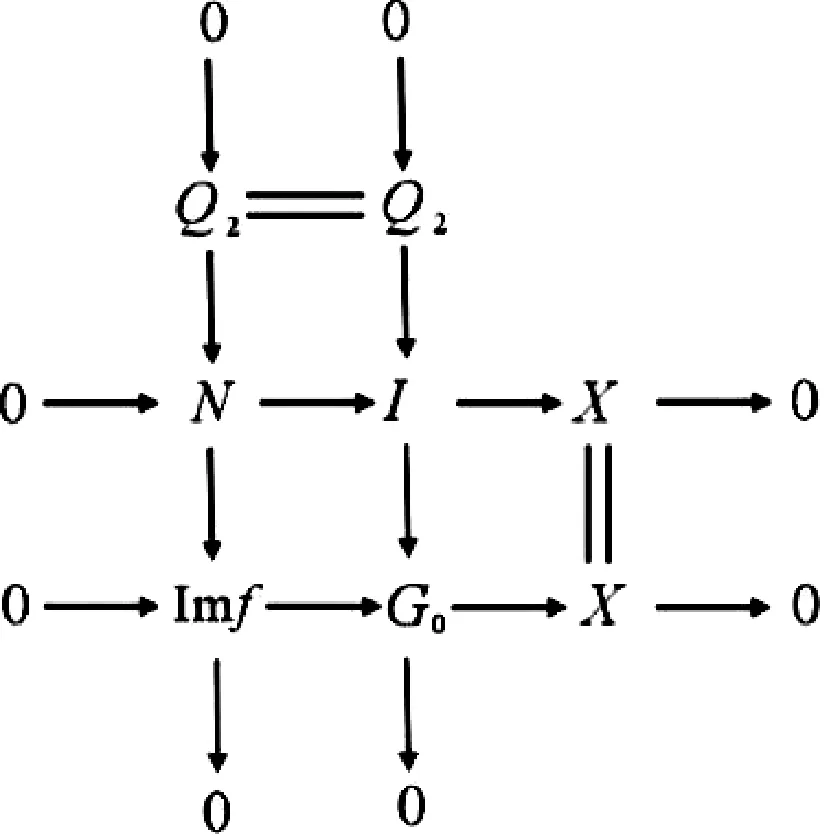
考察该图中的第一列和正合序列0→A→G1→Imf→0的拉回图

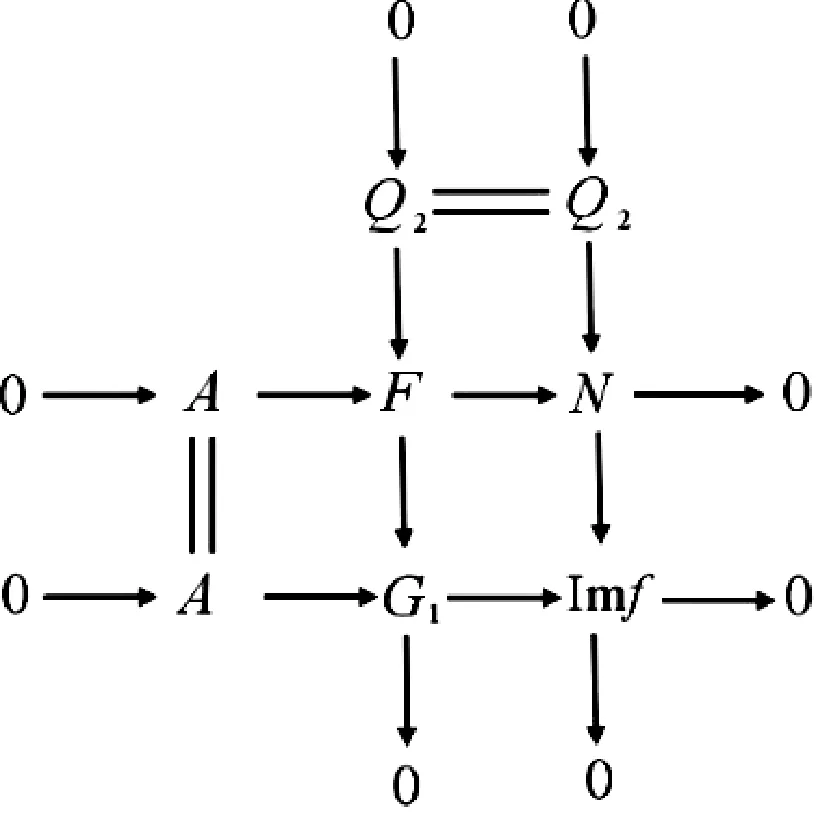
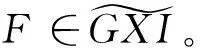
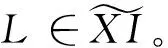
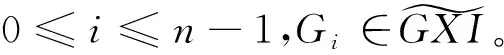
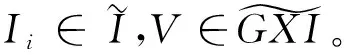
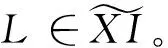
证明 (1)对n进行归纳。

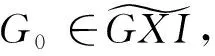
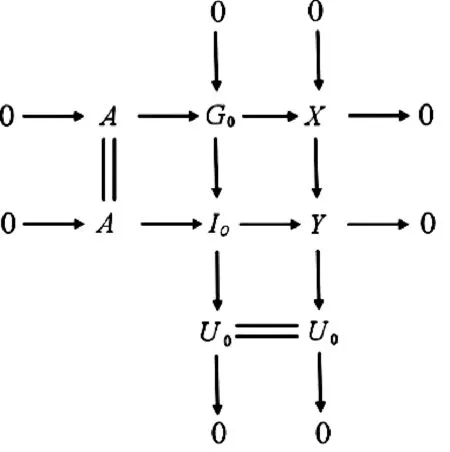
得所需的正合序列0→A→I0→Y→0和0→X→Y→U→0。

设n≥2且有正合序列

0→A→Gn-1→Gn-2→…→G1→G0→X→0,

0→A→Gn-1→Gn-2→K→0,

0→K→Gn-3→…→G0→X→0。

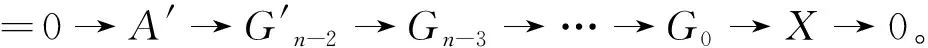
对复形的正合序列P重复此过程,由归纳假设知,存在正合序列

0→A′→In-2→In-3→…→I1→I0→X→0,

0→X→Y→U→0。

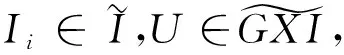
0→A→In-1→In-2→…→I1→I0→Y→0。

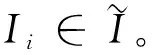
(2)类似于(1)可证。

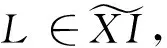
最后,有了以上性质的支持,我们得到利用定义GorensteinX-内射复形的方法构造出的复形仍然是GorensteinX-内射复形。

定理1 设X∈C(R),则X是GorensteinX-内射复形当且仅当存在GorensteinX-内射复形的正合序列

证明 ⟹设X是一个GorensteinX-内射复形。由定义3知存在内射复形的正合序列

…→G1→G0→G-1→G-2→…,

使得X≅Ker(G-1→G-2)且对任意X-内射复形G,上述序列是HomC(R)(G,-)正合的。因为内射复形是X-内射复形,并且X-内射复形是GorensteinX-内射复形,所以正合序列G即是GorensteinX-内射复形的正合序列。

⟸设存在HomC(R)(L,-)正合的GorensteinX-内射复形的正合序列

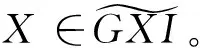
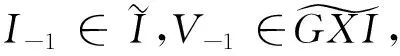
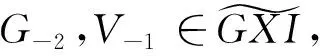
0→X→I-1→I-2→…,(*)

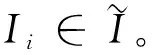
…→I1→I0→X→,(**)

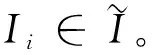
…→I1→I0→I-1→I-2→…,