基于超声变幅杆纵弯复合椭圆振动系统的计算

蒙永红，贺西平，赵海军，王金霞

(1.兰州理工大学 技术工程学院通识教育中心，甘肃 兰州 730050；2.陕西师范大学 物理学与信息技术学院，陕西 西安 710119)

近年来，在工业、国防、农业、环保和城市建设等各行各业，功率超声技术发展迅速，提高了工作效率和产品质量，将该技术用到生活中已经成为不可阻挡的趋势。超声加工作为功率超声的应用，是目前在特种加工中的常用加工技术[1-3]。其工作原理主要是通过换能器产生振动，经过变幅杆的放大，再传递至工具杆，以不断辅助冲击磨料而对工件表面进行加工。我国最早研制的设备是用于对深孔的加工，清华大学[4，5]、北京航空航天大学[6，7]、陕西师范大学[8，9]等国内高校在超声变幅杆在超声加工技术领域的应用方面都做了理论和实验性的探究。北京航空航天大学张德远等人对二维超声椭圆振动加工技术进行了研究，证明了椭圆超声加工不仅能够降低工件表面的粗糙度，而且能降低切削力，节省加工成本[10]。陕西师范大学贺西平教授对超声换能器和超声加工做了专题性介绍[11]。

超声变幅杆作为超声振动系统的重要部分，自从郎之万超声换能器被研制成功后，超声变幅杆也被研究者们提出，他们将超声变幅杆与换能器连接，以获得更高的能量[12]。20世纪中叶，随着超声技术的发展，开始出现了不同类型的超声变幅杆。80年代我国超声学者林仲茂编写了关于超声变幅杆方面的专著，系统地介绍了有关超声变幅杆方面的知识，时至今日依旧是广大超声学研究者们参考的重要资料，为初学者们提供了很好的基础教材。同期，考虑到超声变幅杆接负载的情况，有学者分析了带负载时超声变幅杆的特性。随着超声加工技术的不断发展，单一的超声变幅杆及超声变幅杆的纵振动已经无法满足技术的要求，复合型的超声变幅杆就被设计出来。2016年，贺西平教授研究了具有夹角型的超声变幅杆，可以实现纵振动方向的改变。随之，扭转振动超声变幅杆[13]、弯曲超声变幅杆振动[14]、纵弯复合超声变幅杆[15]以及纵扭复合超声变幅杆[16]等开始被研究。

超声椭圆振动系统是超声椭圆振动加工的核心部分。超声椭圆振动加工具有超声纵向振动和超声弯曲振动加工的共同优点，且分离效果明显，在超声加工过程中能够实现刀具、工件和切屑三者的完全分离，能够降低切削力，减少切削热等。超声椭圆振动一般是通过两个或以上的单向振动复合而成的，可以有纵-弯复合、双弯曲复合、纵-扭复合等多种组合形式，不同的加工要求需要不同的振动系统[17-18]。

本文计算了换能器-圆柱和换能器-阶梯超声变幅杆弯曲振动、纵振动频率相同时输出端为复合椭圆振动系统的尺寸。设定换能器的频率是20kHz，画出纵向振动和弯曲振动的谐振曲线，最终可根据曲线的交点计算出纵-弯同频共振时杆的相关几何尺寸，最终设计出所需的超声椭圆振动系统。为了验证设计的正确性，利用有限元软件仿真了超声椭圆振动系统。结果表明，在固有频率为20kHz时，可以实现超声振动系统纵向振动和弯曲振动复合成超声椭圆振动。

1 超声换能器的设计

超声换能器是超声加工系统的重要组成部分，超声换能器能够实现电能与机械能之间的相互转换，具有较高的收发灵敏度和能量转化效率，且使用的频率范围较宽。压电陶瓷片在高功率工作中容易发生断裂，为了能给压电陶瓷片施加一定的机械强度预应力，使用预应力螺栓将超声换能器的前后盖板和压电陶瓷片接在一起，使陶瓷片在压缩状态下工作，防止陶瓷片断裂。本文设计的超声换能器频率为20kHz，图1为换能器的结构简图。换能器的材料为45#钢，几何尺寸分别如表1所示。

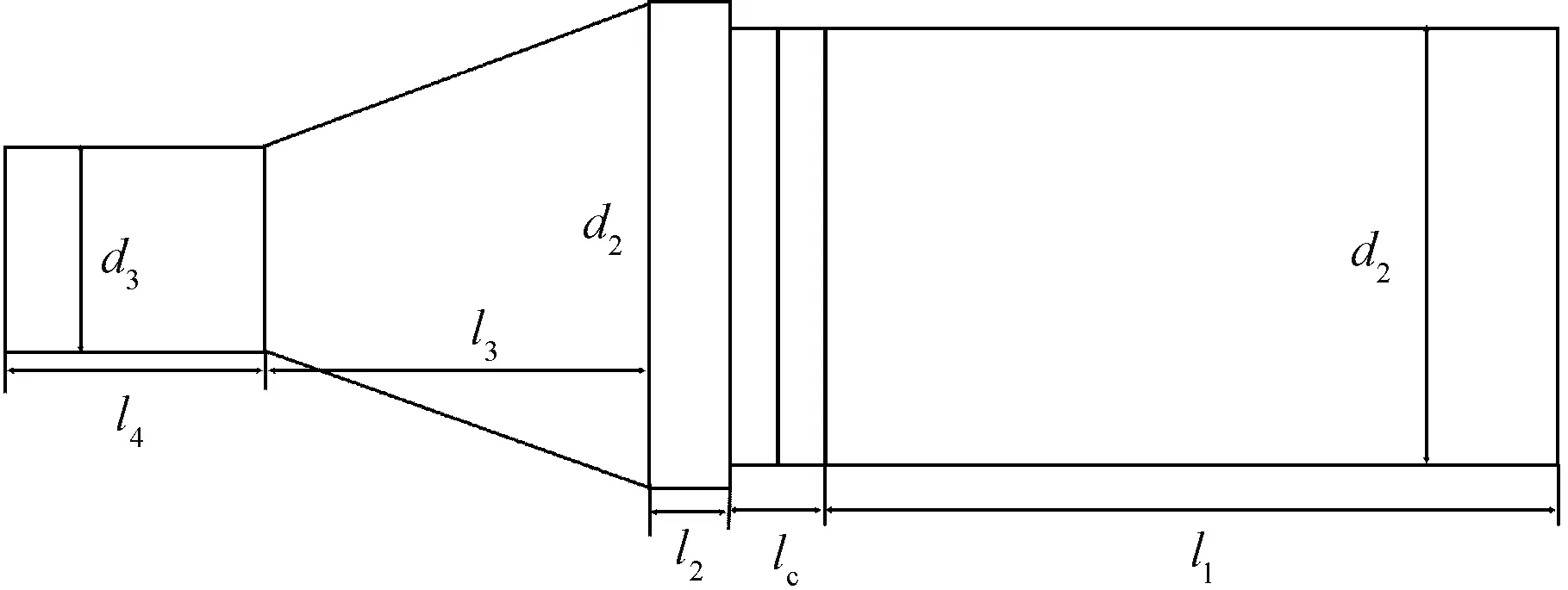
图1 超声换能器结构简图

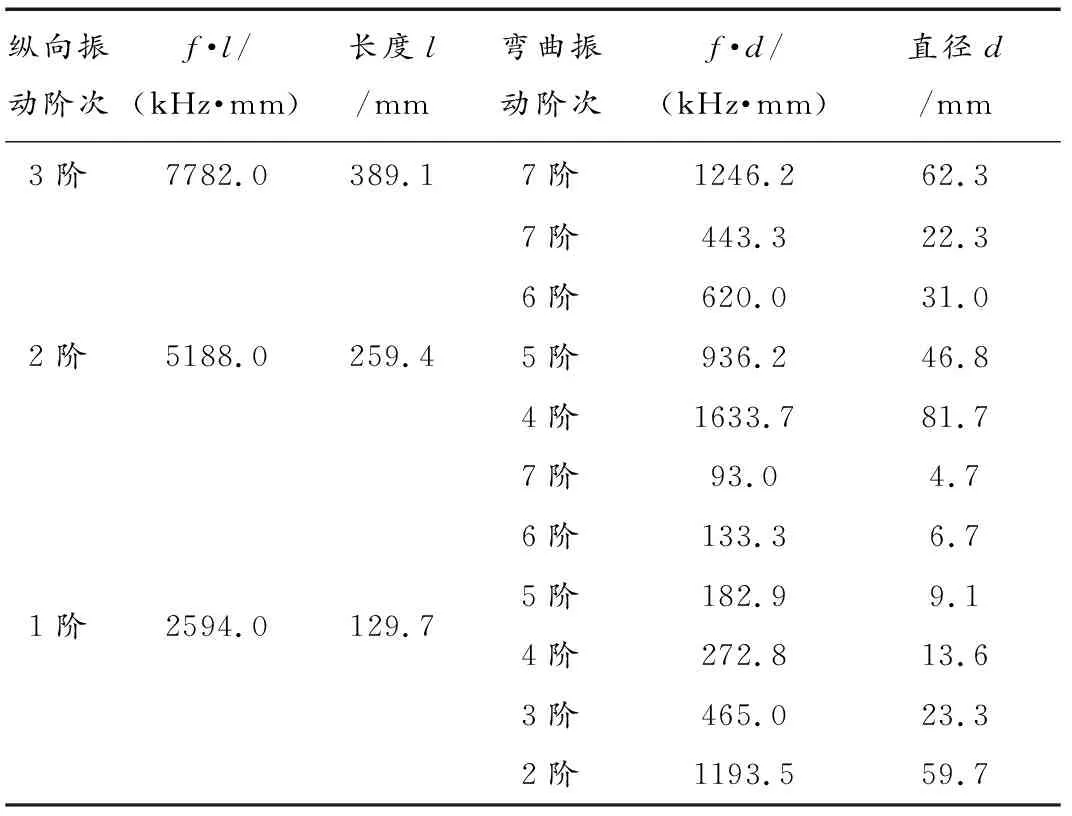
表1 变幅杆的特征参数

2 换能器-圆柱变幅杆纵弯复合椭圆振动系统的计算

对于圆柱形超声变幅杆，纵向振动频率方程

(1)

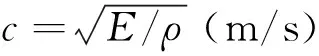
由Timoshenko杆理论得，圆柱形超声变幅杆的弯曲振动频率方程是

sh(γl)cos(γl)=0

(2)

C=ρA1/EI1。

其中ρ是材料的密度，A为横截面的面积，E为杨氏模量，I为转动惯量，ω为角频率，G为剪切模量。

通过对圆柱形超声变幅杆的纵向振动方程和Timoshenko理论变幅杆的弯曲振动方程的推导，计算在共同的超声振动频率时变幅杆的几何尺寸，确定超声振动系统能够实现超声纵弯复合型的超声椭圆振动。变幅杆纵向振动与弯曲振动的几何关系尺寸如图2所示。

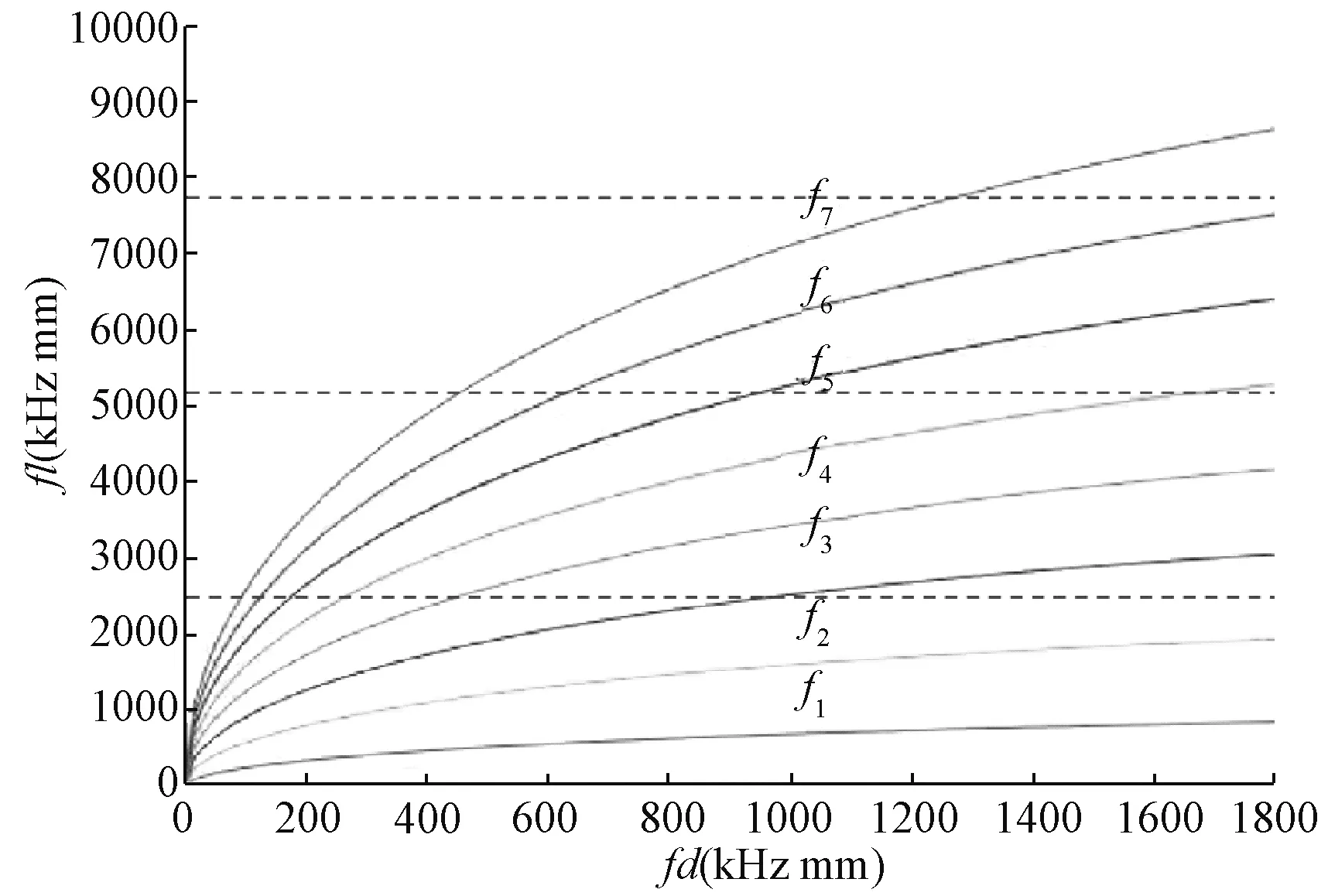
图2 圆柱形变幅杆纵、弯振动的谐振曲线

图2为圆柱形超声变幅杆纵弯谐振的频率曲线图，图中虚线表示杆的纵向振动，曲线表示杆的各阶弯曲振动。纵坐标表示变幅杆的频率和杆的长度的乘积，横坐标表示变幅杆的频率和直径的乘积。分别取纵向振动和弯曲振动谐振曲线的交点坐标值，如表2所示。

表2 纵弯复合超声椭圆振动系统参数

根据表2的计算可得圆柱形超声变幅杆纵向振动和弯曲振动在同频时变幅杆的几何尺寸，我们选择纵向和弯曲的振动阶次分别是n=2和n=6。即圆柱形超声变幅杆的长度为260.0mm，直径为30.0mm。则振动系统的几何参数如表3所示。

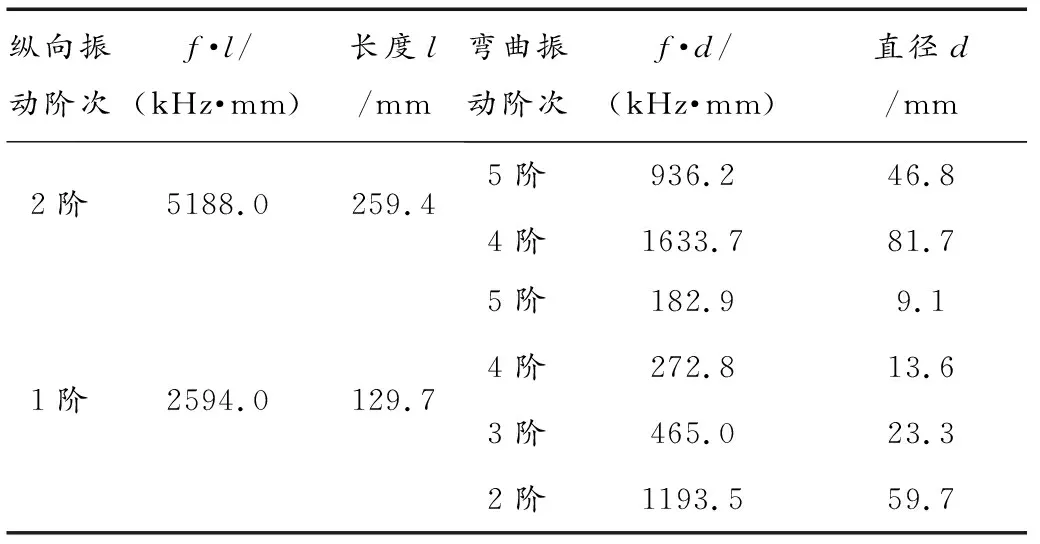
表3 纵弯复合超声椭圆振动系统参数

采用有限元软件建立纵-弯复合超声椭圆振动模型，考虑压电陶瓷材料的特性，用Solid 187和Solid 5单元分别对材料为45#钢和PZT-4的压电陶瓷进行单元划分。图3是超声椭圆振动的模型图,图4和图5分别为超声振动系统纵振动频率f=22061Hz和弯曲振动频率f=21933Hz。

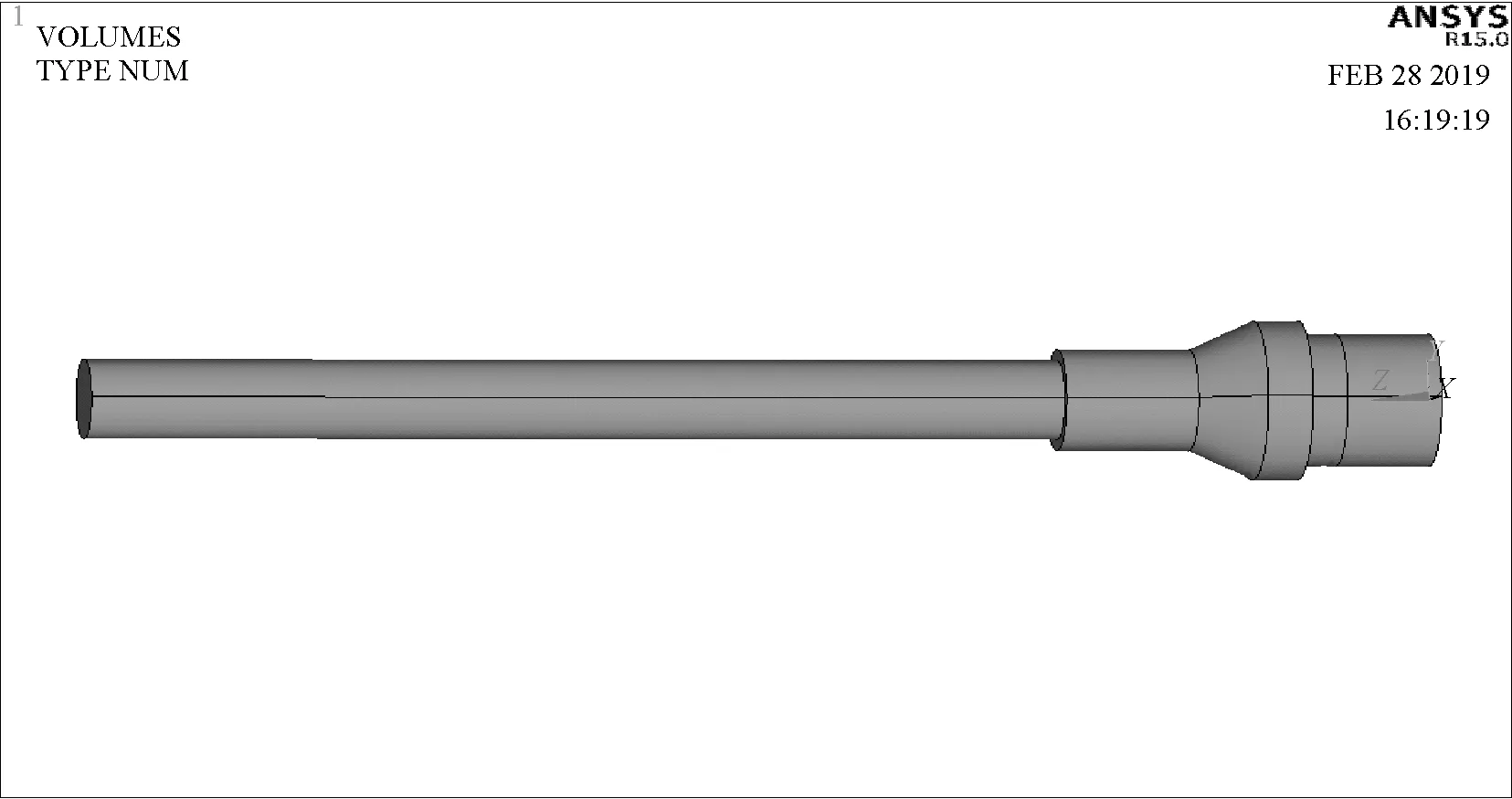
图3 超声椭圆振动的模型图

图4 f=22061Hz第2阶超声纵振动系统振型

图5 f=21933Hz第6阶超声弯曲振动系统振型

对纵弯超声椭圆振动系统的有限元仿真结果可知，设计的换能器-圆柱超声椭圆振动系统，在频率20kHz时，可以实现纵振动和弯曲振动复合成椭圆振动。

3 换能器-阶梯变幅杆纵弯复合椭圆振动系统的计算

如图6所示，基于对圆柱形超声变幅杆的超声椭圆振动的设计，在此基础上保持换能器的几何尺寸不变，计算阶梯形超声变幅杆的几何尺寸。

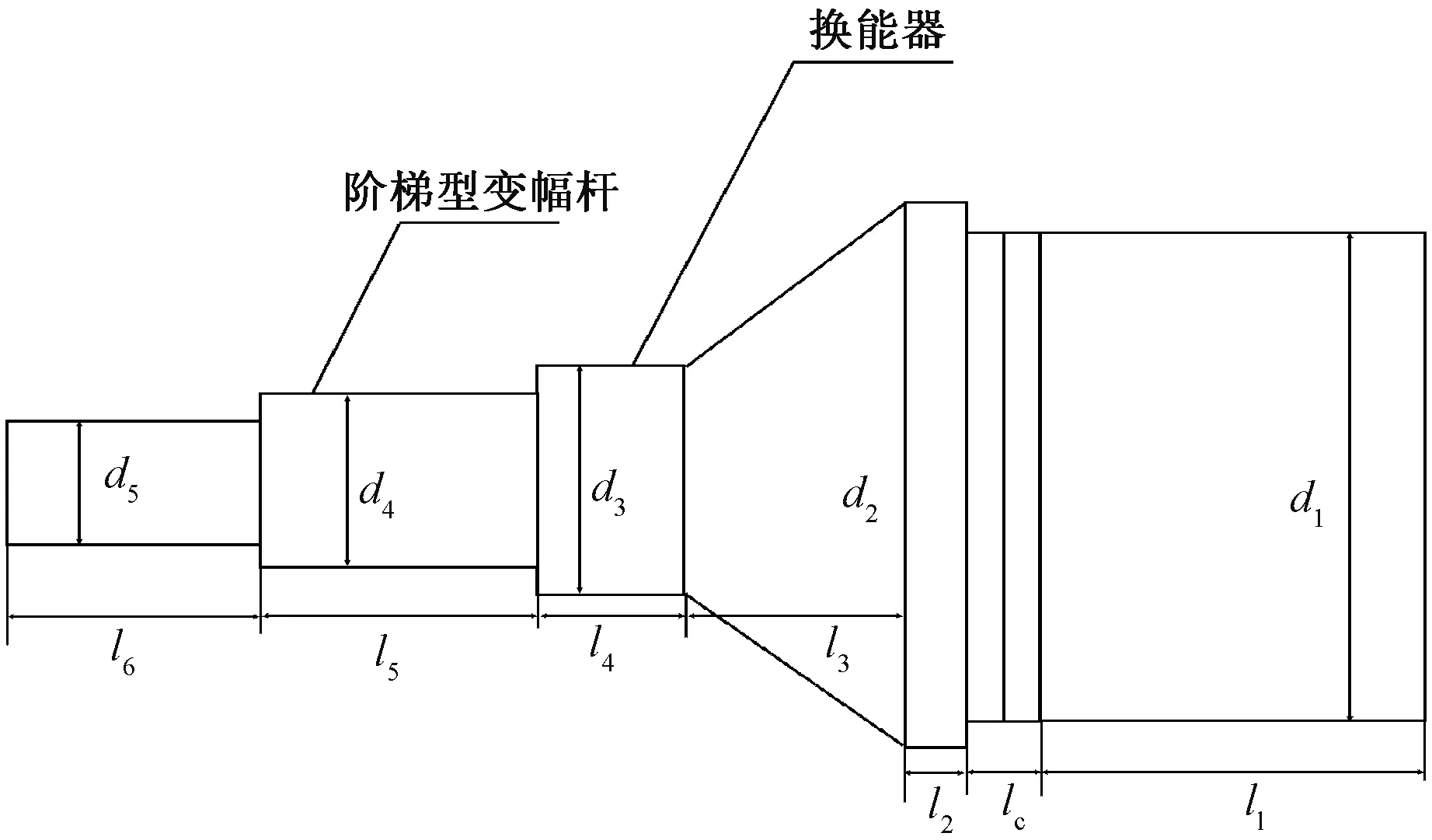
图6 超声振动系统结构

图7为阶梯形超声变幅杆纵弯谐振的曲线，分别取纵向振动和弯曲振动谐振曲线的交点坐标值，如表3所示。

图7 阶梯形变幅杆纵向振动、弯曲振动的谐振曲线

根据表3的计算可知阶梯形超声变幅杆纵向振动和弯曲振动在同频时变幅杆的几何尺寸。同理，我们选择纵向和弯曲的振动阶次分别是n=1和n=3。则杆的直径大小为d=23.0mm，长度为l=130.0mm。最终得系统的几何尺寸如表4所示。

表4 纵弯超声振动系统的尺寸

采用有限元软件计算纵-弯复合超声椭圆振动系统，用Solid 187和Solid 5单元分别对材料为45#钢和材料为PZT-4的陶瓷网格划分。图8和图9分别是超声振动系统纵向振动频率f=20554Hz和弯曲振动频率f=19917Hz。

图8 f=20554Hz第1阶超声纵振动系统振型

图9 f=19917Hz第9阶超声弯曲振动系统振型

通过有限元软件对超声椭圆系统建模、网格划分和加载求解等过程，最终计算的其对纵弯超声椭圆振动系统的有限元仿真结果可知，第一阶纵振动频率f=20554Hz，第九阶弯曲振动频率f=19917Hz，结果如图9所示。结果证明，设计的换能器-阶梯超声椭圆振动系统，在频率20kHz时，得能够实现纵振动和弯曲振动复合成椭圆振动。

4 结论

本文设计了纵-弯复合型超声椭圆振动系统。在换能器的频率是20kHz时，计算超声变幅杆在此频率时纵向振动和弯曲振动的长度和直径，得到超声变幅杆的几何尺寸，设计了超声椭圆振动系统，并利用有限元软件仿真计算超声椭圆振动系统。结果表明，在频率为20kHz时，可以实现超声纵向振动和超声弯曲振动复合成椭圆振动系统，理论计算结果与有限元计算结果误差较小，从而验证了理论设计是正确的。此理论设计方法为纵弯复合型超声椭圆振动系统的设计提供了依据，同时在超声加工领域难加工的硬脆性等材料上有一定的利用价值。