不同储能对多时间尺度风电消纳特性对比研究
普智勇,张冬蕊,尹学卫,王 骁,窦体春
(1.中广核新能源投资(深圳)有限公司云南分公司,云南 昆明 650000; 2.哈尔滨工业大学 电气工程系,黑龙江 哈尔滨 150001)
随着环境问题及能源结构问题的日益严峻,电力行业逐步加大了清洁能源的发展力度[1]。风电作为近年来大力发展的新能源之一,由于其典型的波动性和间歇性,给电力系统运行及稳定带来了新的挑战。储能装置由于可以实现对电力系统实时不平衡能量的吸收或支持,在新能源电力系统中具有非常广阔的应用前景[2]。其中,电池储能和超级电容储能均具有快速响应的特点。不同的是,超级电容储能具有较高的功率密度和较低的能量密度;而电池储能具有较高的能量密度和较低的功率密度[3-5]。此外,电池储能装置的使用寿命受其充放电深度影响较大,而超级电容的循环寿命受其运行方式的影响较小[6]。因此,对比研究两种储能系统的不同性能,对充分、高效、经济地利用不同储能装置进行风电消纳具有重要的意义和价值。
与此同时,风电功率可以视作不同时间尺度的分量叠加[7]。根据这个特点,可以结合不同时间尺度的风电功率特性及不同储能系统的特点,探究不同储能对多时间尺度风电消纳的特性,对储能参与新能源消纳策略的制定提供参考和指导。
针对混合储能系统与多时间尺度风电功率消纳问题,国内外学者从控制策略,时间常数选取等方面进行了研究。文献[8]采用离散傅立叶变换和经验模态分解的方法,实现了对实时风电功率的分解,提出了一种微电网混合储能容量配制方法;文献[9-10]基于综合能源系统基本网络结构,从经济性角度对多元储能系统进行了规划;文献[11]基于电热混合储能原理,以对弃风功率的最大化消纳为目标,提出了一种微电网运行策略。目前针对电池及超级电容储能系统对风电功率消纳问题的研究大多停留在优化调度层面,缺少对两种储能系统内部的精细化建模,无法反映储能系统或装置实时的电压和功率波动信息。因此,本文基于电池和超级电容储能系统的工作原理及内部结构,对两种储能系统进行细致的数学模型刻画,在此基础上,研究储能系统在消纳多时间尺度风电功率过程中的动态表现,对储能系统特性的研究和评估具有实用性的价值和意义。
本文从适用性和经济性角度,基于电池和超级电容储能工作原理建立数学模型,探究了对不同时间尺度风功率消纳过程中,两种储能的电压、功率及能量变化过程,对两种储能对多时间尺度风电功率消纳特性进行了对比分析和评估。
1 储能系统数学模型
基于电池和超级电容储能工作原理建立电池和超级电容储能系统模型,在建模过程中进行以下假设[12]:
(1)忽略环境影响因素,如环境湿度、环境温度等外部因素对模型内部元件的影响,认为设定模型参数不随充放电过程的进行而发生变化;
(2)忽略个体间差异,认为所有元件单体是完全一样的。
1.1 电池储能系统模型
电池储能单体通过串并联的方式组成电池储能系统模型[12]。本文采用等值电路法建立电池单体模型,如图1所示[13]。
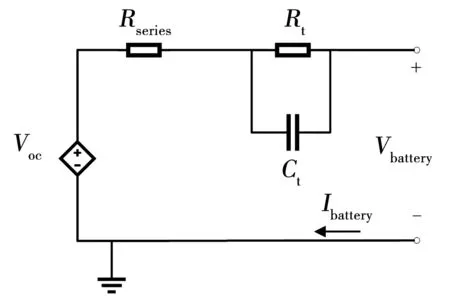
图1 电池储能单体模型
其中,Vbattery和Ibattery代表电池两端的电压与电流;Rt、Rseries和Ct分别代表电池内部的电阻与电容参数;Voc代表电池的开路电压。模型内部参数如表1所示。
对应的电池单体传递函数为
(1)
本文考虑128个电池单体通过串并联的方式组成用于风电功率消纳的电池储能子模块(额定功率20.48kW)。根据风电功率及容量需求,可以适当确定一定数量的子模块以及其连接的方式。
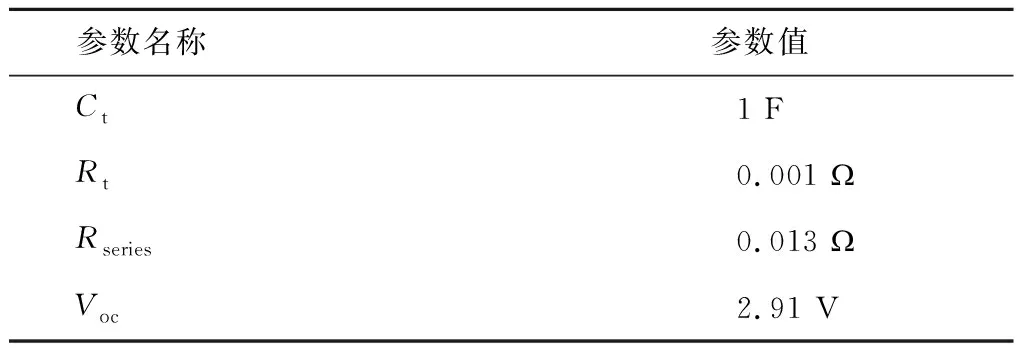
表1 电池模型内部参数
1.2 超级电容储能系统
类似地,超级电容储能系统也是由若干个超级电容储能子系统组成的。超级电容单体通过串并联的连接方式组成超级电容储能子系统。超级电容储能单体模型如图2所示。

图2 超级电容储能单体模型
其中,超级电容端电压和端电流分别为Vsc和Isc;R0-R2、C0-C2分别为对应的电阻和电容参数。超级电容储能单体模型参数如表2所示。超级电容单体对应传递函数为
(2)
本文考虑超级电容储能子模块共由800多个超级电容储能单体组成,总电容为56.8 F,额定电压为199.8 V,总容量为293 Wh。
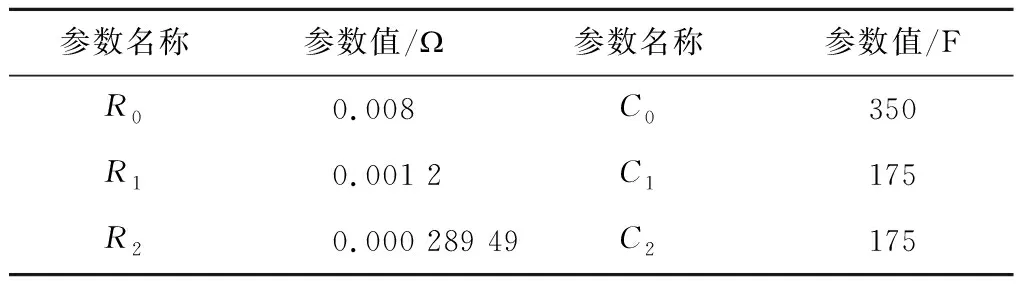
表2 超级电容模型内部参数
基于电池和超级电容单体模型,结合储能系统内部单体串并联关系,应用戴维南电路等效原理,可以对电池和超级电容储能系统的传递函数进行推导,在Matlab/Simulink软件平台搭建用于风电功率消纳过程分析的储能系统数学模型。
2 风电功率的重构
可以应用于风电功率的多时间尺度特性研究的非平稳信号处理方法很多,如EMD(经验模态分解法)是其中应用较广泛的一种[14]。
本文采用某风电场实测数据,应用EMD方法,对该60 MW风电厂功率进行分解。该风电场24小时功率及其幅频特性曲线如图3所示。
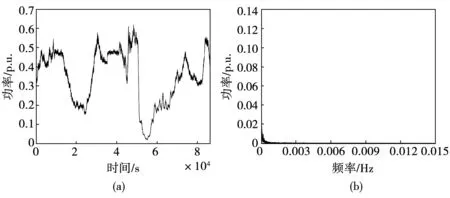
图3 原始风电功率及其幅频特性曲线
以中心频率为基准,对风电功率进行重构。将风电功率按照中心频率高低依次重构为高频分量——中心波动频率高于0.016 Hz,即波动周期为1 min以下的功率分量;中频分量——中心波动频率范围在0.000 278~0.016 Hz,即波动周期为1 min至1 h范围内的功率分量;低频分量——中心波动频率小于0.000 278 Hz,即波动周期在1 h以上的功率分量。经过分解与重构后,如图4至图6所示,是时域和频域内不同分量的特点。

图4 高频分量功率及幅频特性曲线
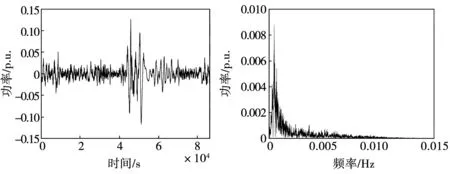
图5 中频分量功率及幅频特性曲线

图6 低频分量功率及幅频特性曲线
风电功率的波动展现出多时间尺度的特性,即风电功率由高频、中频、低频波动分量共同构成。随着中心波动频率的减小,风电功率的波动幅度逐渐升高。不同频率的波动分量展现出了不同的波动特性将影响不同储能系统的动态表现。
3 应用实例
相较于其他类型的储能设备,电池和超级电容储能的响应速度快,可以及时响应快速波动的功率扰动,且由于其储能成本相对高昂,不适合用于大幅度低频功率波动的风电消纳。因此,综合考虑两种储能的技术特点及经济性,仅使用电池和超级电容储能消纳风电的中高频扰动分量。
首先,对比研究两种储能吸收快速波动的风电功率分量的表现。功率、电压、能量响应曲线分别如图7至图9所示。

图7 高频信号下电池(左)及超级电容(右)功率曲线
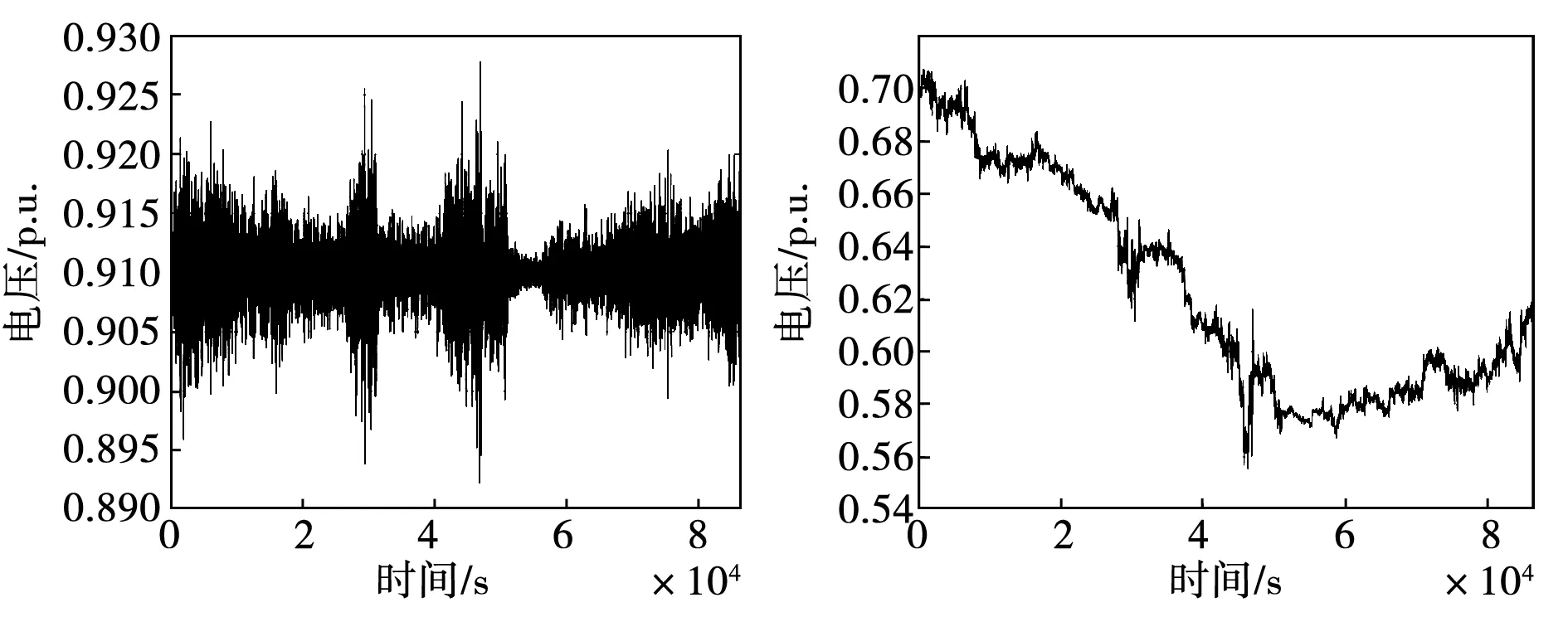
图8 高频信号下电池(左)及超级电容(右)电压曲线

图9 高频信号下电池(左)及超级电容(右)能量曲线
在消纳高频风电波动分量过程中,由于高频分量对应的功率需求幅值较小,电池和超级电容均可以及时跟随风功率波动,且其能量偏移具有类似的趋势。但由于超级电容能量密度的限制,超级电容能量偏移幅值远大于电池。在高频功率波动下,电池和超级电容处在不断地小幅度充放电工况中,电池的电压在开路电压附近上下波动,这一行为会对电池的寿命造成较大的影响。而对于超级电容来说,其使用寿命受充放电方式等因素影响微乎其微。
其次,对比研究两种储能吸收中等速度波动的风电功率分量时的表现。两种储能的功率、电压、能量响应曲线分别如图10至图12所示。
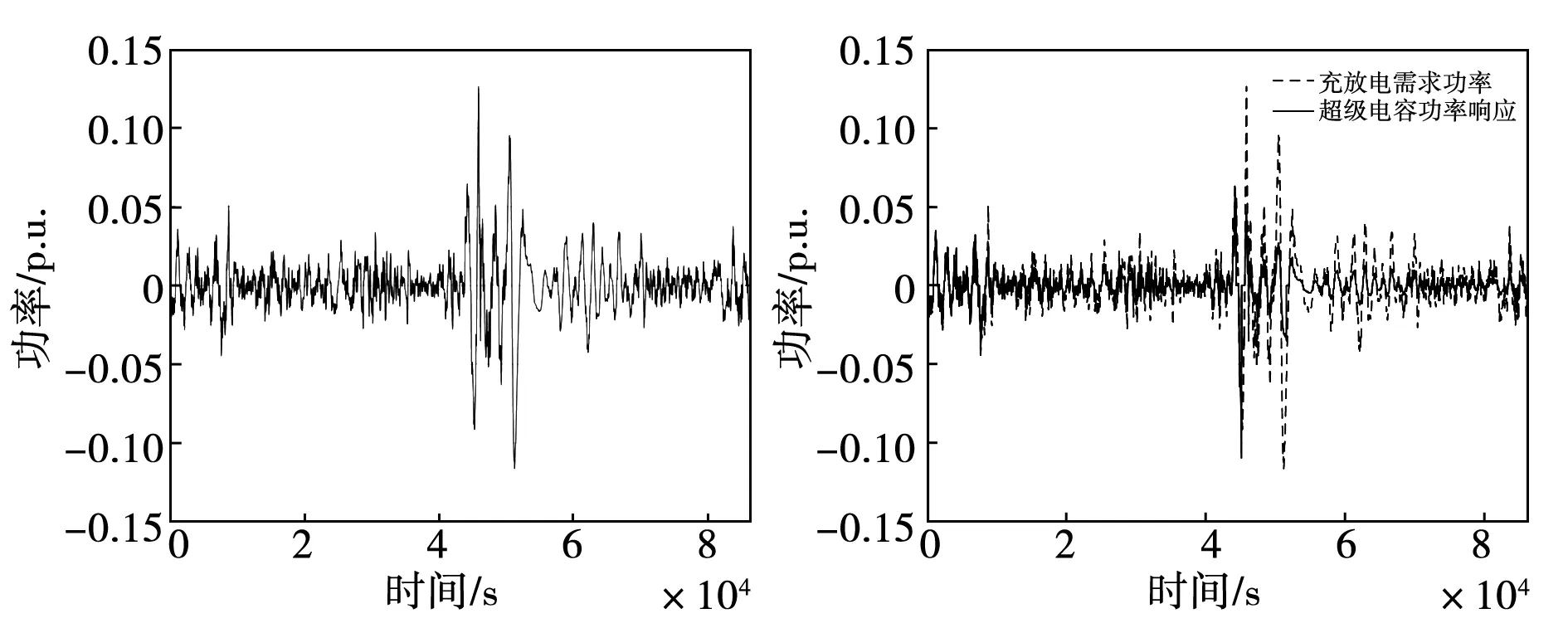
图10 中频信号下电池(左)及超级电容(右)功率曲线

图11 中频信号下电池(左)及超级电容(右)电压曲线
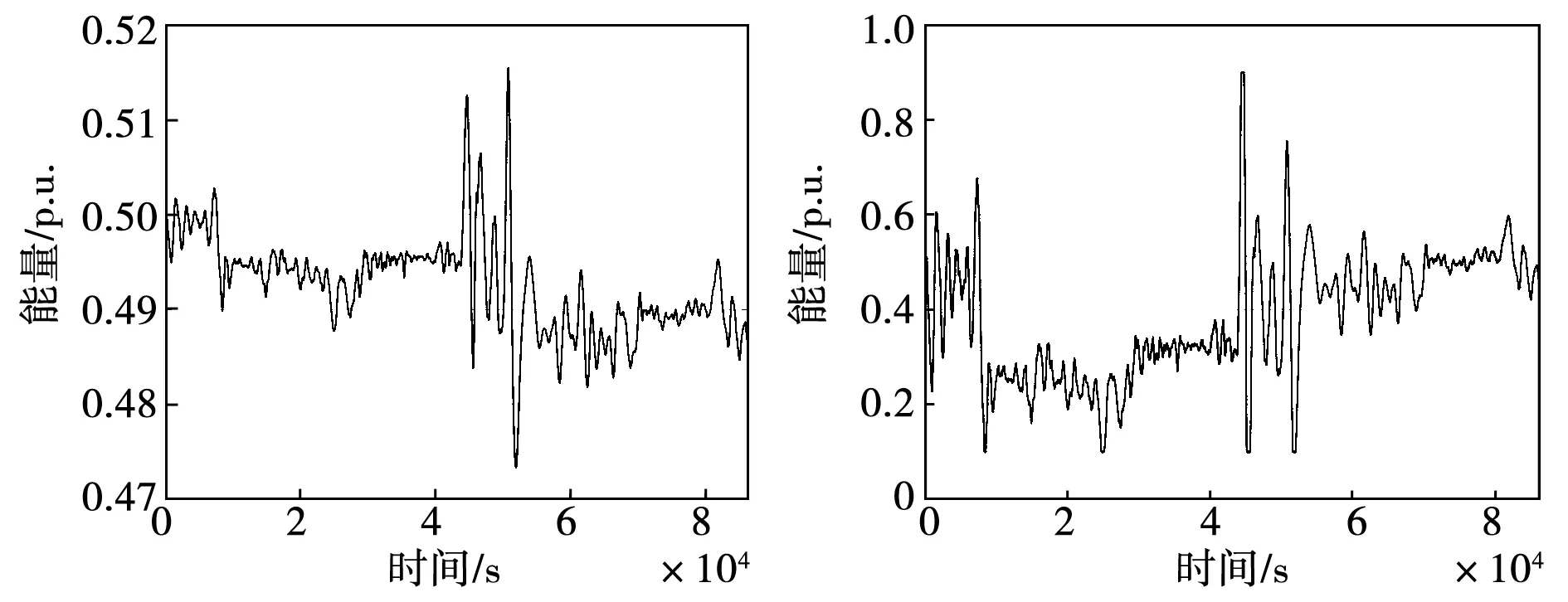
图12 中频信号下电池(左)及超级电容(右)能量曲线
在消纳中频波动风电功率的过程中,超级电容出现了因能量密度限制,无法跟踪风电功率波动的情况。在频繁较大幅度放电的工况下,超级电容多次出现放电至最小允许容量的情况,在此过程中仅能响应充电功率需求,而相比之下,由于电池储能的能量充足,仍可以实时跟踪风电消纳的功率需求。
在此基础上,由于电池储能使用寿命受充放电方式影响较大,采用雨流计数法对消纳高频及中频风电功率过程中电池的偏移曲线进行数据提取和压缩,得到单次充放电次数与充放电深度关系如图13所示[15]。在高频功率波动影响下,电池充放电次数多且深度小;在中频功率波动影响下,电池充放电次数较少且深度大。在高频扰动下,电池寿命的折损程度更高,经济性较差。
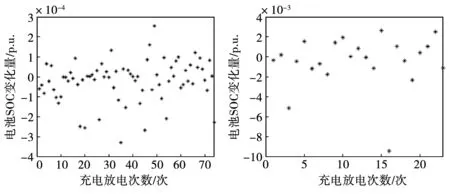
图13 高频(左)和中频(右)信号下电池充放电深度
由以上结果,在实际风电消纳过程中,从经济性角度首先应避免电池储能频繁小幅度充放电工况对其使用寿命造成影响;其次,从风电消纳效果角度,应避免超级电容进行较大功率波动幅度的充放电工况,以避免其因能量密度不足造成的完全充放电现象。因此,在风电功率消纳过程中,可以考虑让超级电容储能响应系统中的波动幅度较小的高频分量,而让电池响应波动频率较小的中频分量,以充分利用不同储能系统的工作特性和特长,达到风电的经济安全消纳目的。
4 结论
(1)将风电功率重构为高、中、低频三部分。其中波动频率高的成分幅值较小,反之较大。
(2)电池储能由于其使用寿命受充放电方式影响较大的局限性,应在工作中避免小幅度充放电的工况频繁产生,从经济性角度更适用于中频段风电功率的消纳。
(3)超级电容储能因其能量密度较小的特点,适用于消纳高频波动的风电功率。在充分利用其功率密度特点的基础上,可以避免能量不足的情况产生。

