中国可再生能源消费与经济增长实证分析
李鹏雁,许文秀
(1.哈尔滨工业大学 人文社科与法学学院,黑龙江 哈尔滨 150001; 2.湖州师范学院 求真学院,浙江 湖州 313000)
0 引言
中国经济的高速增长,对于能源的需求越来越大,而传统化石能源的不可再生性和高污染性已使其不再占有优势[1]。相比之下,可再生能源具有开发潜力大、清洁、可循环再生等多重优点。各国越来越重视可再生能源的研究开发,不断完善相关法律法规,改善政策环境[2]。目前,我国已成为全球最大的节能、利用可再生能源的国家,这对我国经济发展意义重大。
能源消费、可再生能源消费和经济增长关系的研究,许多专家学者在不同时间段、不同区域使用的方法、得出的结论不尽相同。Nicholas使用ARDL边界测试这种较新的方法对坦桑尼亚1971~2006年间的能源消耗和GDP的因果关系进行了研究,得到两变量间有着长期稳定均衡关系且能源消费可以拉动GDP增长的结论[3]。Seyyedeh Fatemeh Naser同样使用该方法,探究所有经合组织国家可再生能源消费对经济增长的影响,发现能够通过提升能源使用效率来促进经济增长[4]。陈操操以北京市1980~2008年间的数据,借助协整检验、VECM模型格兰杰因果关系检验对北京市能源消费和实际GDP间的关系进行了研究[5]。张优智利用1980~2011年间的经济数据,在构建若干个各不相同的STR模型的基础上,分析出能源消费和经济增长间具有长期动态非线性关系,而且两个变量间存在显著的区间转制动态特点[6]。从现有的文献看,大部分是对能源消费和经济增长两个变量间关系的探究,可再生能源消费与经济增长关系的分析较少,而本文正是从这个点着手展开研究。
1 数据的选择和处理
本文使用的是我国1978~2017年的GDP、可再生能源消费量的经济数据,其来自于国家统计局网站及相关年份的《中国统计年鉴》,为了消除通货膨胀因素的影响,须借助CPI指数对名义GDP进行一系列处理得到分析所需的实际GDP数据。同时,对实际GDP、可再生能源消费量进行了自然对数处理,表示为lnGDP、lnne,避免变量时间序列的性质发生变化,有助于促使变量时间序列趋势线性化,得到平稳的时间序列,同时可以解决模型中可能会出现的异方差问题。实证分析所需数据的详细处理方式如下:
本文以1978年的居民消费价格指数为基准,即CPIt(1978年=1),将1978~2017年的上年=100的CPI指数数据,按照以下公式:CPIt(1978年=1)=CPIt-1(1978年=1)*CPIt(上年=100)/100,算出各年以1978年为基期的CPI指数。接着将根据当期市场价格计算得到的国内生产总值(即名义国内生产总值)数据,按照公式:实际国内生产总值=名义国内生产总值/CPIt(1978年=1),算出相应年份的实际国内生产总值数据。可再生能源消费量数据的选择:可再生能源包括风能、太阳能等能源,本文先选取相关年份的能源消费总量数据和可再生能源消费占能源消费总量的比重值数据,从而算出所选区间内每年我国可再生能源消费量的数值(单位:万吨标准煤)。
2 实证研究
2.1 建立向量自回归(VAR)模型
VAR模型不同于基于经济理论反映变量间关系的传统计量经济方法,它能对变量间动态联系做出一个严谨缜密的说明,广泛应用于变量间关系的研究之中。本文建立包含实际GDP、可再生能源消费(ne)两个变量的二元VAR模型。接着为模型选择一个最优滞后阶数,表1中第一行是进行最优滞后阶数选择所依据的几个方法,星号对应着每种标准所选择的最优滞后阶数,可以看到,上述方法中绝大多数都选择2作为最优滞后阶数,故模型最佳滞后阶数为2。
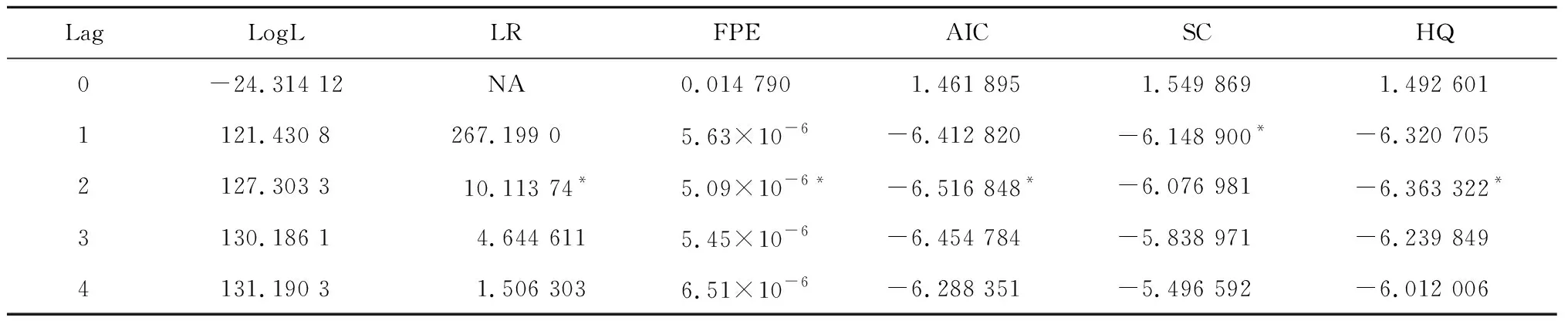
表1 滞后阶数选择
借助Eviews 8.0软件得到VAR模型:
lnGDPt=1.563lnGDPt-1-0.023lnnet-1-0.607lnGDPt-2+0.076lnnet-2-0.004+μ1tR2=0.999 041 R2=0.998 924
lnnet=0.221lnGDPt-1+0.955lnnet-1-0.014lnGDPt-2-0.180lnnet-2+0.086+μ2tR2=0.997 025 R2=0.996 665
可以看到,VAR模型的拟合效果良好,两个内生变量方程的可决、调整可决系数都在99%以上。可再生能源消费对经济增长的影响,第一期是负的0.023,第二期是正的0.076,影响有所增强。从整体来说,可再生能源消费是促进实际GDP增长的一个重要因素,两个经济变量间存在相关关系。
2.2 序列平稳性检验
在时间序列的分析中,首先应对所使用序列的平稳性进行检验。本文使用ADF检验法。
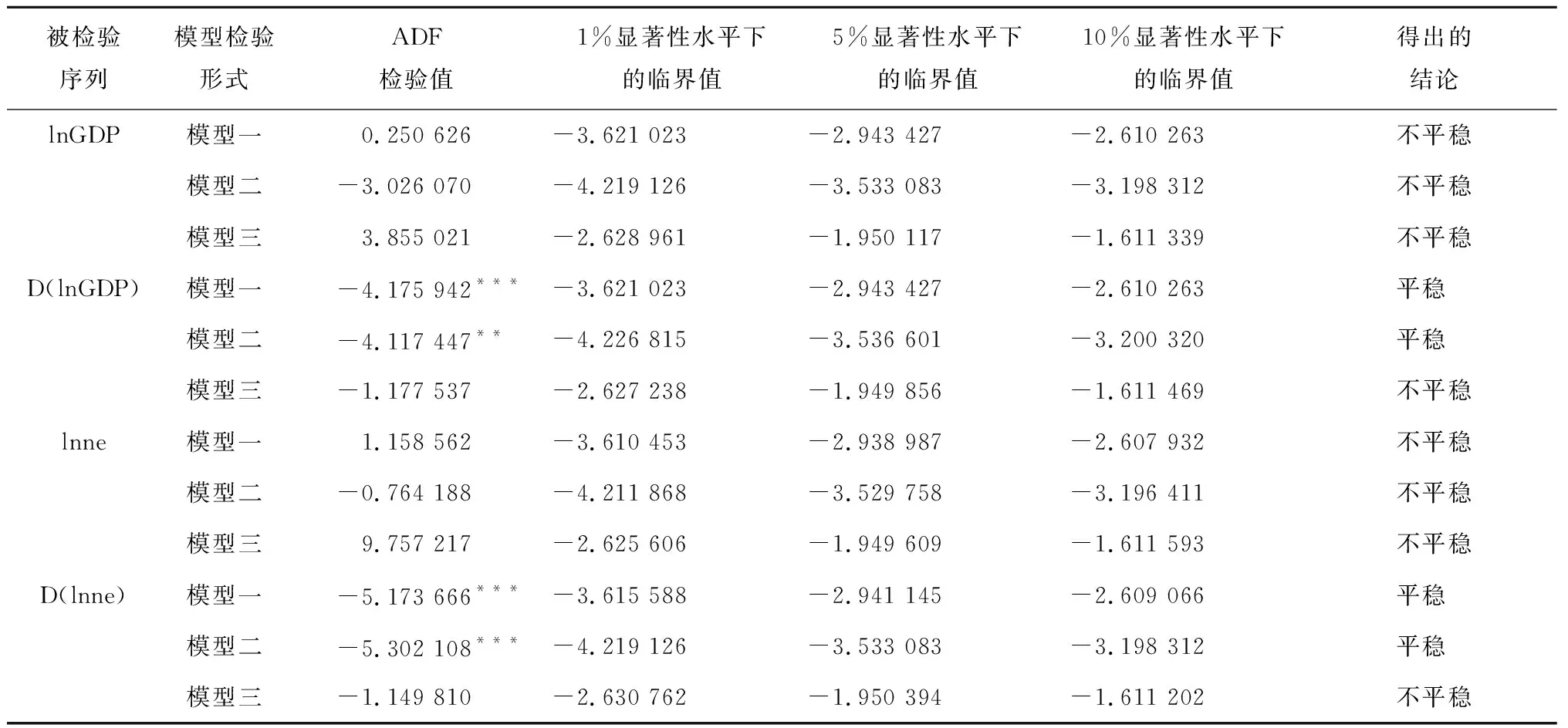
表2 实际国内生产总值、可再生能源消费的ADF单位根检验结果
ADF单位根检验中,显著性水平是指犯错误的概率。由表2可知,在常数项与线性时间趋势项三种不同的检验模型下,对数变换后的实际GDP、可再生能源消费量的水平序列的ADF单位根检验值均大于1%、5%、10%显著性水平下的临界值,此时应接受零假设,即这两个变量对数变换后的水平序列都有单位根,为非平稳序列。接下来对这两个宏观经济变量的自然对数序列做一阶差分处理,得到D(lnGDP)、D(lnne)两个一阶差分序列,然后对其进行单位根检验,可以看到,模型一中,序列的ADF检验值都比1%显著性水平下的临界值要小,此时接受备选假设。lnGDP、lnne序列均是经过一次差分后就平稳了,故这两个序列均是一阶单整序列,满足协整检验的要求。
2.3 协整检验
尽管lnGDP、lnne序列本身是非平稳的,但是两个序列的线性组合却有可能将趋势项的影响互相抵消掉,成为一个平稳的时间序列,即两者间具有长期稳定均衡关系。本文检验实际GDP与可再生能源消费间的协整关系,选择约翰森检验法[7]。该法是以VAR模型为基础检验回归系数的方法,适用于两个或多个变量的协整关系检验。前面已构建了最优滞后阶数(p=2)的VAR模型,下面是对实际GDP、可再生能源消费自然对数序列进行约翰森最大似然协整关系检验的结果。

表3 迹检验

表4 最大特征值检验
宏观经济变量间协整关系的数目要根据特征根迹检验及最大特征值检验的结果来确定。从检验“变量间不存在协整关系”的原假设开始,由表3和4可知,检验结果中迹检验值为19.486 72,大于5%显著性水平下的临界值(18.397 71),最大特征根值为17.770 52,也比对应的5%显著性水平下的临界值(17.147 69)要大,此时应接受备选假设;接着检验“变量间至多有一个协整关系”的原假设,对应的迹检验值(1.716 198)比5%显著性水平下的临界值(3.841 466)小,最大特征根值为1.716 198,小于5%显著性水平下的临界值(3.841 466),故接受至多存在一个协整关系的原假设。由此可知两个宏观经济变量间存在1个协整关系。
2.4 建立向量误差修正(VECM)模型
协整关系仅反映了变量间的长期关系,是一个静态的体系,不能反映变量短期波动对被解释变量的影响。而实际GDP与可再生能源消费之间具有长期稳定均衡关系,故能继续构建VECM模型探究变量短期波动的影响。由表1知,无约束的VAR模型最优滞后阶数是2,因此将VECM模型滞后区间设成“1 1”,下面得到VECM模型的估计结果。
VECM模型:
ecmt=lnGDPt-0.445lnnet-4.635-0.058trend
D(lnGDPt)=-0.271ecmt-1+0.748D(lnGDPt-1)-0.031 D(lnnet-1)+0.022+0.000 16trend
R2=0.469 085 R2=0.404 731
D(lnnet)=0.411ecmt-1-0.001D(lnGDPt-1)+0.0595D(lnnet-1)+0.062 3+0.001trend
R2=0.278 161 R2=0.1906 66
VECM模型给出了协整方程;而且建立了将误差修正项当做回归量的一阶差分VAR模型,对应着VECM模型中的几个内生变量方程。得到的VECM模型的可决系数很高,是0.469 085,调整的可决系数是0.404 731,说明模型的拟合效果很好;得到的协整关系方程:ecmt=lnGDPt-0.445lnnet-4.635-0.058trend,从中可以看到,可再生能源消费增加一个百分点时,实际GDP将增加0.445个百分点[8]。由此可以看到,可再生能源消费对实际GDP增长起着非常重要的作用。
短期内,实际GDP、可再生能源消费量的变动是经济变量短期的变动和变量间长期稳定均衡趋势共同作用的结果,而短期变量间的均衡关系偏离系统长期稳定均衡关系又导致了经济变量短期的变动。
从短期内实际GDP增长的角度看,VECM模型中等式右端一次差分项系数依次是0.748、-0.031,其中D(lnGDPt-1)的系数0.748表示上一期实际GDP的增长率增加一个百分点时,当期实际GDP增长率将增加0.748个百分点;D(lnnet-1)的系数-0.031表示上一期可再生能源消费量的增长率增加一个百分点时,当期实际GDP增长率将下降0.031个百分点,这种情况实际是极有可能存在的,尽管短期内增加可再生能源消费,但在实际资本存量、劳动力投入以及包括政策因素等在内的其他影响实际GDP的各因素的共同作用下,下一期实际GDP有可能增加也有可能减少,即使相比上期增长了,那增长率也有可能下降,即可再生能源消费对实际GDP的弹性值(-0.031)为负的情况出现。
对于误差修正项的系数即调整系数,若其比零小,说明误差修正项对实际GDP的增长起到正向作用,反之则起负向作用,这里误差修正项的系数为-0.271,则系统对于实际GDP的增长有增强作用,即短期变量间的均衡关系偏离长期均衡时,模型会以-0.271的调整力度将其从不均衡状态调整到均衡状态。
2.5 格兰杰因果关系检验
上述分析可知:实际GDP、可再生能源消费间具有长期稳定均衡关系,因此,可以直接对两者进行格兰杰因果关系检验,结果如下。

表5 格兰杰因果关系检验
由表5可以看到,在对零假设“lnne不是lnGDP的格兰杰原因”的检验中,滞后一到七期中,对应的P值均比0.05大,即在95%的置信水平下,应当接受零假设;而在滞后八、九、十期中,对应的P值均比0.05小,即在95%的置信水平下,应当拒绝零假设。总体来看,短期内,可再生能源消费不是实际GDP变动的格兰杰原因,长期范围内,可再生能源消费是经济增长的格兰杰原因。
对零假设“lnGDP不是lnne的格兰杰原因”的检验中,其中滞后一期和二期中,对应的P值比0.05小,即在5%的显著性水平下,应拒绝零假设;而在滞后三期到十期中,对应的P值均大于0.05,即在5%的显著性水平下,应接受零假设。因此,从整体来看,可认为短期内,实际GDP是可再生能源消费的格兰杰原因,长期内,则实际GDP不能促进可再生能源消费增长。
2.6 脉冲响应函数
研究某个内生变量对于来自误差项的冲击的响应,可以通过脉冲响应函数图反映出来。
由图1可知,当期给可再生能源消费一个正向标准差大小的冲击后,实际GDP并没有立刻作出反应,而在第一期末第二期初,实际GDP对可再生能源消费冲击的反应才开始表现出来,表现为较小的负向反应,反应从第二期开始到第九期呈逐渐增强趋势,达到一个最大响应值,并在以后保持稳定水平[9]。

图1 lnGDP、lnne对各变量一个标准差冲击的响应
图1中,可再生能源消费对实际GDP一个标准差大小的正冲击的反应从当期末第二期初开始表现出来,最初为较小的负向反应,从第二期至第十期呈明显增强趋势,达到一个较高的水平后,保持稳定水平。
通过比较可发现,实际GDP一个标准差大小的正冲击对可再生能源消费的正向作用要明显大于后者一个标准差大小的正冲击对前者的影响,即经济增长对可再生能源消费的影响更大。
2.7 方差分解
方差分解可得到每个随机扰动的贡献程度,进而对不同结构冲击的重要程度做出评价。
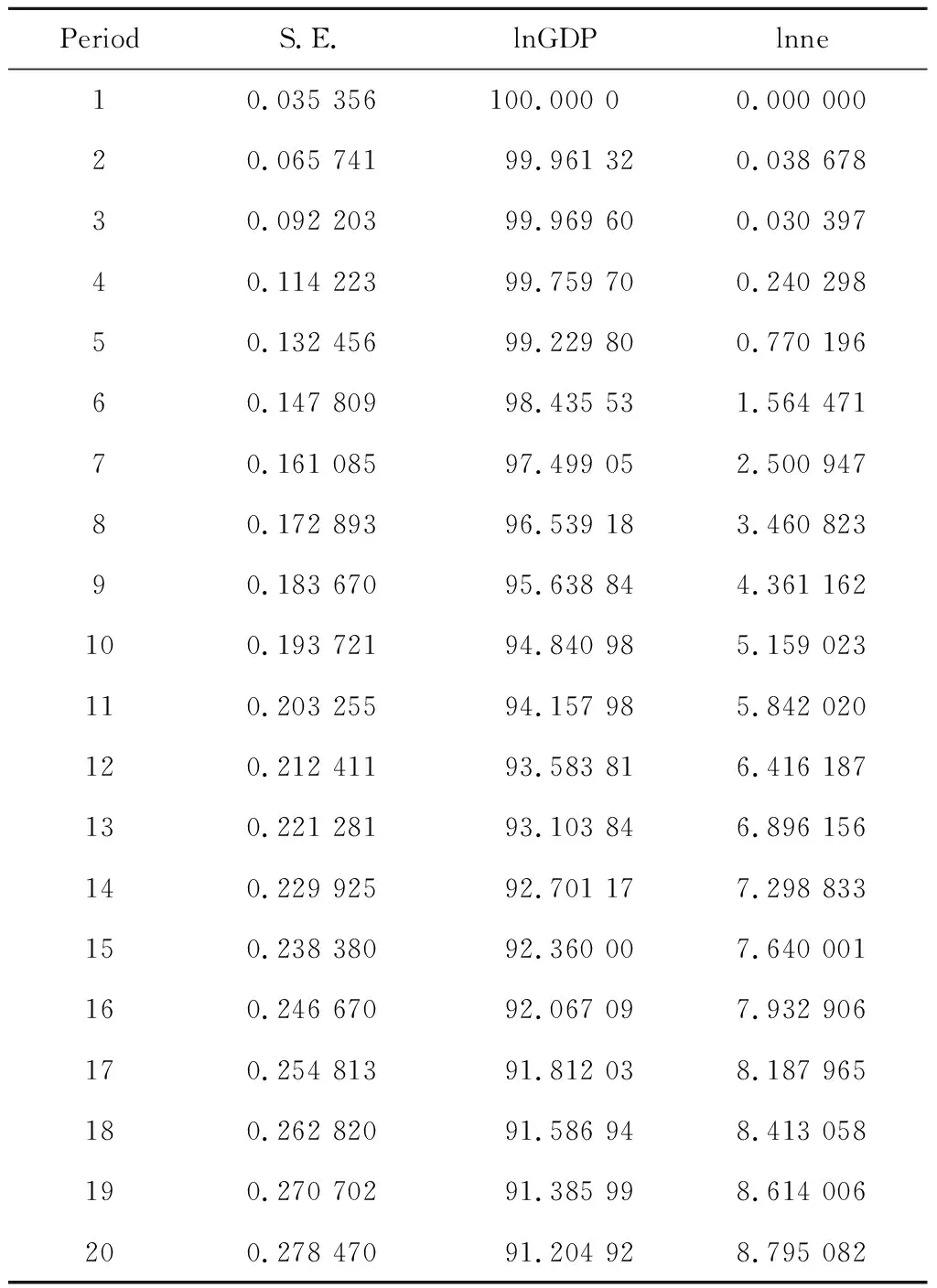
表6 lnGDP的方差分解结果
表6反映了实际GDP、可再生能源消费变动对实际GDP变动的影响程度。可以发现:实际GDP的变动,受自身误差项的冲击的影响很大,但随着时间的推移,这种影响在逐渐减弱,从第一期的100%降到第二十期的91%;可再生能源消费变动对实际GDP变动的影响程度从总体上来说是比较大的,呈现持续增长的趋势,第二十期达8.8%。总体来说,可再生能源消费是促进经济增长一个重要因素。
3 可再生能源发展的政策建议
通过上述分析可知,可再生能源消费对经济增长起着重要的拉动作用。在未来,可再生能源消费是大势所趋。因此,应进一步推进可再生能源产业发展,本文从增加市场需求、提高技术水平、降低开发利用成本、完善相关政策法规角度提出了政策建议。
3.1 推动可再生能源市场的实际需求
必须从源头出发解决市场需求不足的问题,让公众认可可再生能源,切实体会到使用可再生能源产品给自身带来的益处。比如,可以先在非再生能源利用中弊端已经明显显露出来的城市设立试点,如北京,北京多从内蒙古购买火电,火力发电带来了严重的污染问题,而若从风力资源充足的内蒙古买风电,既可推动当地风电产业快速发展、风能的开发利用,又使北京、石家庄沙尘暴上游的风力风速减小,缓解了这些城市的沙尘暴问题,使当地居民受益。与此同时,政府部门可以制定政府采购的导向政策、适当采取强制性的配额制措施、在最大程度上给购买者税收和价格方面的优惠或补贴。
3.2 加大技术研发投入 提高科技发展水平
当前经济呈下行趋势,加之可再生能源投资本身风险很大,许多企业将减少相关技术的研发投入。因此,不能再单靠市场的力量,政府要提供大力支持,加大科研资金投入力度;制定合理科学的科研规划;加快寻找与太阳能、生物质能等可再生能源开发利用密切相关的新技术;对现有的科研资源进行整合,提倡由科研能力领先的企业、科研院所、高校实验室通力合作共同完成技术研究任务;加强和各国的人才交流,充分实现优势互补[10]。
3.3 进一步完善相关产业政策及制度体系
政府部门应进一步完善可再生能源产业发展的管理及决策机制,促使相关部门之间高效合作、科学决策;有条件的话,设立一个专门负责可再生能源开发利用的机构,负责开发利用中的管理、决策、监督等事务。另外,政府部门应继续致力于完善可再生能源设备、产品的标准体系,检测认证制度及违规严惩制度,从而进一步完善我国可再生能源交易市场的准入制度和监查制度,促进市场不断趋向合理化。

