特质波动率存在性及其影响研究
——基于沪深A股
李 欣
(安徽工业大学,安徽 马鞍山 243000)
一、引言及文献回顾
传统的投资组合理论认为,只有系统性风险需要得到风险补偿,而像特质波动率等非系统性风险可以通过投资组合消除,不需要风险补偿。然而现实的金融市场并不是完全有效市场,由于卖空限制,风险偏好和信息不对称等原因,有一部分非系统性风险无法分散,会影响投资者的预期收益水平,而部分无法分散的风险与预期收益之间的负相关关系被称为特质波动风险。基于Fama-French三因素模型,结合我国股票市场的实际,用流通市值比代替账面市值比对我国沪深A股特质波动风险的存在性进行研究。
特质波动风险对于资产组合预期收益的作用,不同的学者之间存在分歧,一部分学者认为特质波动风险与股票的预期收益率成正相关关系。Black,Jensen和Scholes(1972)通过实证研究发现特质波动率影响股票的预期收益,这与资本资产定价模型中的非系统性风险不影响收益的结论相悖[1]。Merton(1987)认为,由于信息不对称和投资者信息分析能力水平的差异,投资者更倾向于投资于自己所熟知的证券,并期望更高的风险溢价。Merton从供求的角度说明了特质波动率和股票预期收益之间存在正相关关系[2]。Goetzmann&Kumar(2004)经过研究发现,由于投资者的教育经历和风险偏好等各种现实因素的限制,投资者不可能通过充分的投资组合对特质波动率进行有效的分散,因此对于无法分散的特质波动率,投资者期待更高的风险补偿,即Goetzmann等认为特质波动率和预期收益率之间存在正向的比例关系[3]。也有一部分学者认为特质波动率与股票预期收益成负相关关系,即股票市场存在“特质波动率之谜”。Ang et al.(2006,2009)基于 Fama-French 模型,研究美国股票市场的特质波动率,发现特质波动率和股票的预期收益之间存在明显的负相关性,而且这种相关性在加入多个风险控制因子后并没有减弱,说明这种负相关性是普遍存在的[4][5]。Guo和Savickas(2010)利用CAPM模型,发现特质波动率和股票收益横截面存在负相关关系[6]。影响特质波动风险的原因主要有两个,其一是私有信息。Lee等(2002)公司信息透明程度是影响股价波动的重要原因。信息越透明,股票特质波动越大,反之股价中含有更大的噪声信息,股票特质波动小[7]。其二是错误定价。Boehme(2009)股票市场更多的体现乐观主义的信息,而忽视了悲观主义的信息,导致了股票价格被高估[8]。我国学者对于股市的特质波动风险的研究主要从卖空限制和异质信念两方面入手进行。杨华蔚和韩立岩(2009)经过实证研究发现,由于中国股票市场缺乏卖空限制,股价更多的体现乐观投资者的行为,导致收益率被高估,这是形成特质波动率的重要原因[9]。李竹薇(2014)利用HP滤波法发现,特质波动率对股票截面收益的作用在不同的期限有不同的表现,在长期,特质波动率与股票收益成正比例关系,在短期,特质波动率与股票收益成反比例关系[10]。刘维奇和邢红卫等(2014)基于Fama-MacBeth三因子模型,对我国股市“特质波动率之谜”的存在性进行研究,发现投资者对于某些股票的偏好是形成特质波动率的主要原因[11]。熊和平和刘京军等(2018)基于分位数回归模型对我国沪深A股进行研究,发现在不同的分位数水平上,特质波动率和股票预期收益之间呈现不同的相关性,在低分位水平下特质波动率与股票预期收益呈负相关关系,而在高分位水平下特质波动率则与股票预期收益之间呈显著正相关关系[12]。本文选取2006年1月至2019年3月上海和深圳证券交易所的所有上市A股为研究样本,利用Fama-French三因子模型对我国特质波动风险的存在性进行研究,发现我国A股市场不存在“特质波动率之谜”,特质波动风险对于股票截面收益的影响是正向的,而这种相关性不受其他因素的影响。
二、数据来源和模型设定
(一)样本来源和数据处理
本文以上海证券交易所和深证证券交易所所有上市A股为研究对象。由于我国于2005年进行了全面的股权改革。所以本文的样本区间为2007年1月至2019年3月。共159个样本数据。为了降低非流通股票在加权过程中的影响,本文所有数据都进行总市值加权处理,所有数据均来自锐思数据库。
样本选取如下:ST、*ST由于股价波动幅度过大,予以剔除,同时剔除已经停牌退市的股票;以中国人民银行公布的三个月定期存款利率进行月度处理后的数据为无风险利率。为保证数据的有效性,只保留月交易量大于等于10天的股票数据。
本文以投资组合的月超额收益率作为被解释变量,投资组合的月超额收益率等于投资组合的月收益率减去月无风险利率。其中月度无风险利率按照中国人民银行公布的三个月定期存款利率经折算后得到的同期月存款利率。所有数据分别按照市值规模以及账面市值比各分为五组,交叉分组共25组,市场溢价因子(MKT)通过股票市场投资组合的月超额收益率衡量,具体公式为:

(其中RMT是市场累计月收益率,RFT是通过央行公布的三个月定期存款利率月处理数据进行计算。)
将上海和深圳所有上市A股按照市值的大小分为两组,大市值组合(B)和小市值组合(S);根据账面市值比分为三组,高账面市值比(H),中等账面市值比(M)和低账面市值比(L)。分组完成后,计算 SMB(小规模市值投资组合减去大规模市值投资组合)和HML(高账面市值比的投资组合减去低账面市值比的投资组合)。
具体公式如下:
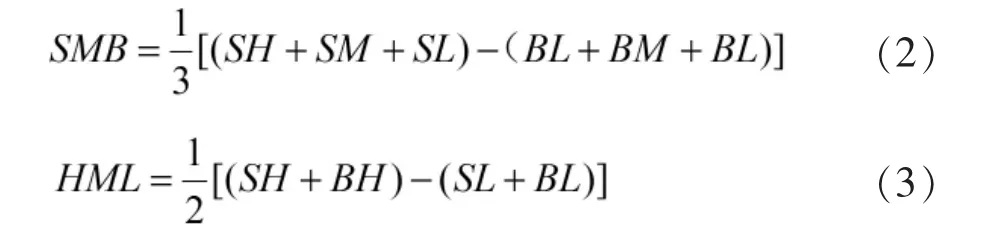
本文基于Fama-French三因子模型,以回归结果的残差项的标准差作为特质波动率的代理变量,回归方程如下:
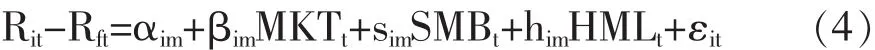
(其中Rit为股票i在考虑现金红利再投资情况下,在第m月t日的回报率,Rft是在第m月t日的无风险利率,MKTt、SMBt和HMLt分别代表在第m月t日的市场风险溢价因子、规模因子和价值因子。αim、βim、sim和him是股票i在m月常数项、市场风险溢出因子、规模因子和价值因子的回归系数。εit是股票i在t日的回归残差。)
特质波动率通过Fama-French三因子模型回归的残差计算:

(N是股票i在第m月的交易天数。std(εit)是股票i在m月回归残差的标准差。)
(二)控制变量的选取
异质信念:交易量和换手率是衡量异质信念的常用指标,但是由于交易量在不同规模的上市公司之间存在较大差异,所以本文以股票的月换手率衡量异质信念。
反转效应:周琳杰(2002)[13]基于深沪两市1995-2000年的股票交易数据,研究发现为期一个月的动量策略的超额收益显著优于其他期限的策略。所以本文以持有期前一个月的累计收益作为衡量股票翻转效应的指标。
市盈率:市盈率是衡量上市公司股票价值的有效指标。
(三)Fama-Macbeth截面回归
以股票的超额收益率作为被解释变量,以特质波动率、三因子回归的系数和上述控制变量作为解释变量,具体回归方程如下:
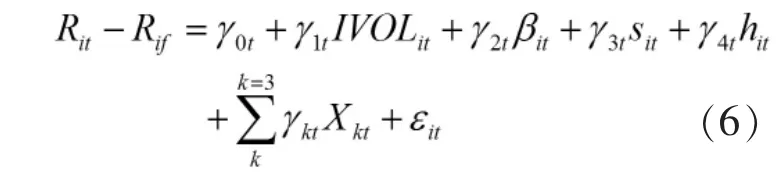
三、实证结果
首先对25组不同市值和账面市值比的超额收益率进行描述性分析。如表1所示,在同一规模的投资分组中,账面市值比越高的组合,其月超额收益率的均值越高。在同一账面市值比的分组中,月超额收益率的均值随着规模的增大而下降。由此可见,规模大小对月超额收益率有负向影响,而账面市值比对月超额收益率有正向的影响。同时,在同一账面市值比的组合中,月超额收益率的标准差随着规模的增大而下降,说明低账面市值比相较于高账面市值比有更大的风险。

表1 25组超额收益率的描述性统计
如表2所示,在总市值加权的条件下,三因子都是正向指标,市场溢价因子和规模因子表现为左偏,账面市值比因子表现为右偏。规模因子对股票市场的平均溢价最大,为1.05%。账面市值比因子的均值最小,为0.20%。市场溢价因子的波动幅度最大,其标准差为8.64%。
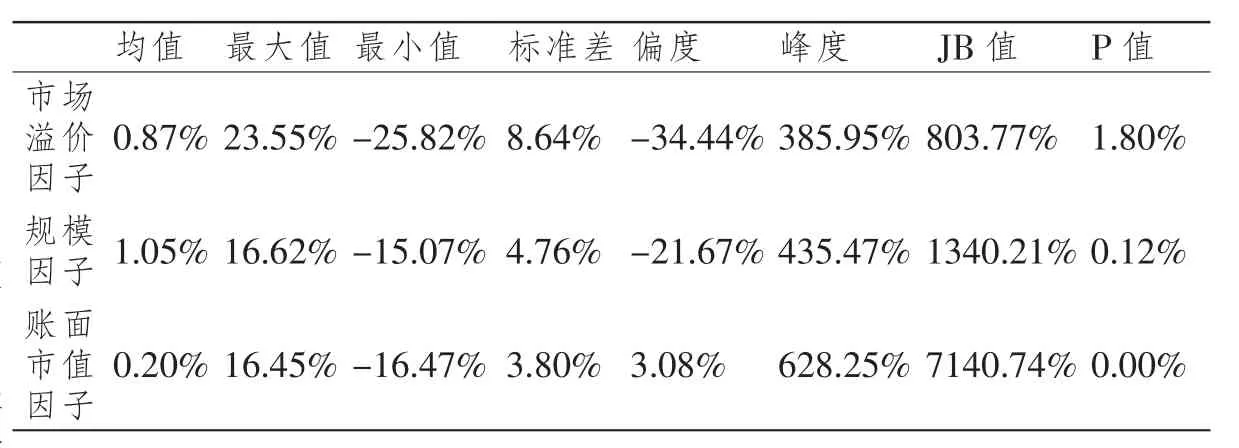
表2 三因子的描述性统计
如表3所示,市场溢价因子和规模因子以及账面市值比都是正相关关系,而规模因子和账面市值比因子是负相关关系。虽然账面市值比和规模因子表现为负相关,但是两者的相关系数是最大的,其绝对值为0.326。

表3 三因子的相关性
如表4(1)所示,市场溢价因子的系数(β)在不同的规模因子和账面市值比的组合中,均稳定在1左右,表明市场溢价因子并没有因为规模因子和账面市值因子的加入而被削弱。同时在所有的组合中,市场溢价因子都在1%的水平下显著。
如表4(2)所示,除最大规模因子分组外,其他组合中的规模因子的系数(s)均为正数,说明规模因子与超额收益率之间基本呈现正相关的关系。而在最大规模因子分组中,除与最高账面市值比组合的系数在10%的水平下显著,其他四组均不显著,可以忽略不计。验证了Fama-French三因子关于规模因子与超额收益率成正比的假设。同时可以看出在同一账面市值比的分组下,随着规模因子的增大,其系数会降低。
如表4(3)所示,除个别组合外,账面市值比因子的系数均为负数,说明超额收益率随着账面市值比的增加而减小。这与Fama-French三因子模型关于账面市值比喻超额收益率成正比的假设相悖。而且在不同的规模因子下,都有表现不显著的账面市值比。
由于我国存在账面美化的成分,可能导致账面市值比失真的现象,所以本文以流通市值比代替账面市值比,进行三因子回归。

表4 多元线性回归结果(1)βim
首先对规模因子和通市值比进行相关性检验,结果如表5所示,规模因子和流通市值比的相关系数为负,与规模因子和账面市值比的相关系数的方向一致,且规模因子和流通市值比的相关系数为-0.018,显著小于规模因子和账面市值比的相关系数。

表5 规模因子和流通市值比的相关性
如表6所示,选择账面市值比的情况下,只有市场溢价因子的回归系数是显著的,而规模因子和账面市值比因子均不显著。而在选择流通市值比的情况下,规模因子在5%的水平下显著,市场溢价因子和流通市值比在1%的水平下显著。所以选择流通市值比作为三因子模型的因子,比选择账面市值比因子更加适合我国股票市场的实际情况。
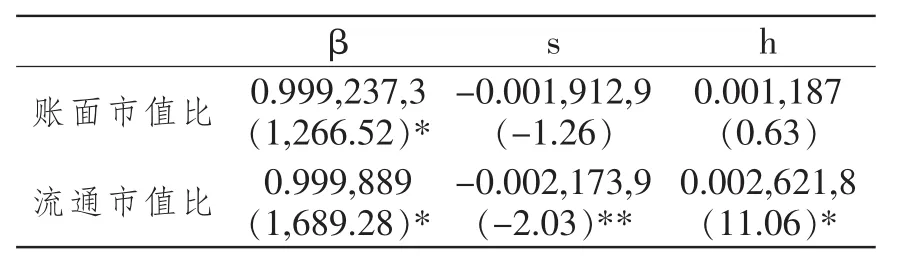
表6 账面市值比和流通市值比较分析
在进行截面回归之前,先进行前期的相关检验。如表7所示,在7个维度下,特征值均不为0,而且条件指数均除了第7个维度外,特征值均小于30,说明变量之间不存在共线性问题。
如表8所示,P值等于0.000,8,显著小于0.05,拒绝原假设,不存在异方差问题。
如表9所示,BG检验的P值为0.008,4,在1%的显著性水平下拒绝原假设,即序列存在自相关问题。
由于序列存在自相关问题,本文用Newey-West来进行修正。如表10所示,特质波动风险、市场溢价因子、规模因子和流通市值比因子都在1%的水平下显著。特质波动风险、市场溢价因子和流通市值比因子与股票的月超额收益率表现为负相关的关系,规模因子与股票的月超额收益率表现为正相关的关系,而这种关系并没有因为加入换手率、前一个月的累计收益和市盈率而发生改变。说明他们对于股票截面收益的影响是稳健的,不受外部效应的影响。
四、结论
本文利用我国A股市场的月股票数据为样本,对我国股票市场特质波动风险对股票截面收益的影响进行分析,并检验了其稳健性。以经过月处理的三因子回归残差为特质波动风险,利用Fama-MacBeth对特质波动风险和股票的月超额收益率进行回归分析,研究结果发现,两者存在显著的正相关性。说明我国A股市场不存在“特质波动率之谜”,随后加入卖空限制、反转效应和市盈率三个控制变量后,发现对特质波动风险的回归系数基本没有影响。所以我国特质波动风险对股票超额收益率的影响是正向的,且这种正相关性不受外部因素的影响。

表7 共线性检验
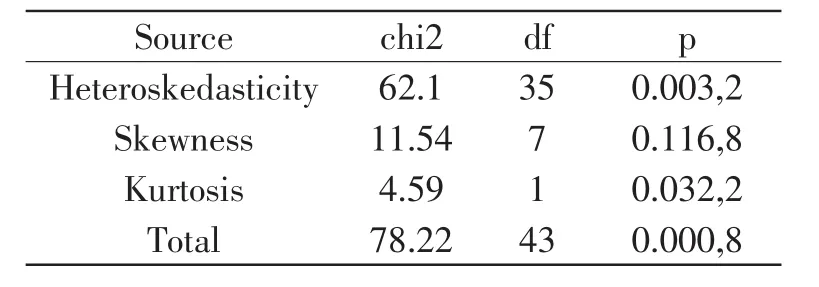
表8 异方差检验

表9 自相关检验
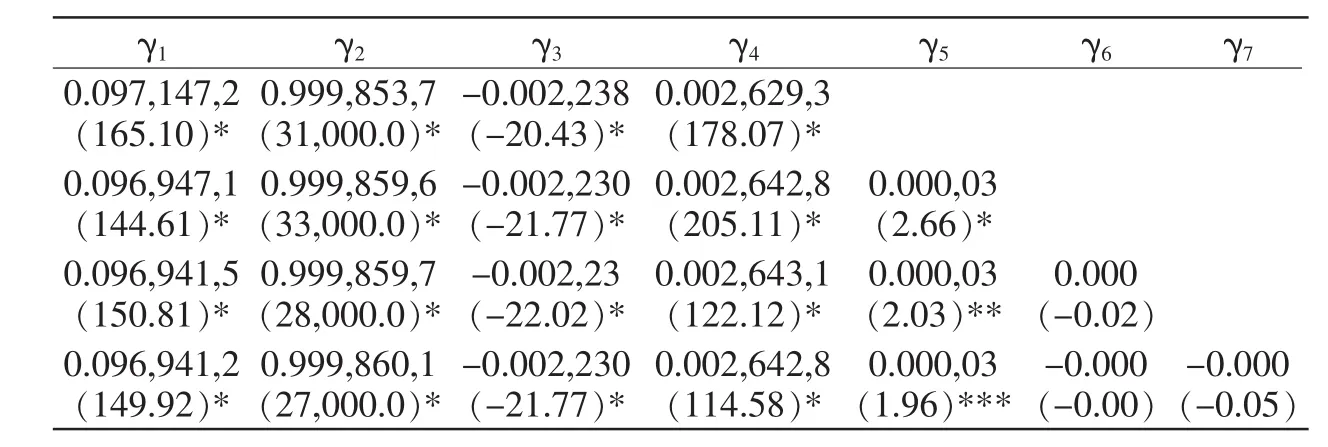
表10 Fama-Macbeth截面回归结果

