波高对波纹管涡激振动特性的影响研究

肖阳宏，李 磊，张兆德，柳振海

（1.浙江海洋大学船舶与海运学院，浙江舟山 316022；2.中国能源建设集团浙江省电力设计院有限公司，浙江杭州 310012）

大量实验和数值研究表明，研究钝体流动理论和应用对解决工程实际问题具有重要作用，尤其是圆柱体结构。BEARMAN[1]，WILLIAMSON，et al[2]，以及JIMÉNEZ-GONZÁLEZ[3]都有对圆柱结构的流固耦合问题进行探讨，流体绕流圆柱结构，会发生边界层分离，导致涡旋脱落从而引起涡激振动问题。当涡旋脱落频率接近结构频率时可能会导致高幅值振荡，这可能会对工程结构造成极大损害，从而导致疲劳破坏。

长期以来，为了减轻这种振动的影响，越来越多的学者进行了大量研究并提出了不同的涡激振动抑制装置。改变普通圆柱体的结构表面形状是常见的被动型控制抑制措施。GAO Yun，et al[4]研究了表面粗糙度对圆柱体涡激振动的影响，比较了具有不同粗糙度的圆柱体升阻力、涡脱频率、振动频率以及位移响应。结果表明，与光滑圆柱相比，粗糙圆柱具有较小的位移响应，较窄的锁定区域和较高的涡流脱落频率。LEE，et al[5]研究了横截面积沿跨度呈正弦变化的圆柱体后面的尾流涡泄，在Re=5×103～2×104之间，实验应用可视化技术测量了两种不同正弦圆柱体后尾流的阻力，平均速度和湍流强度分布，并与相同直径的普通圆柱体进行比较，在Re=104时，其中一种模型的阻力系数降低了约22%。尾流结构在顺流方向上显示出周期性变化。尾流宽度在圆柱体后面的区域中扩展，涡流形成区域变长，涡流引起的波动得到抑制，从而减小了作用在圆柱体上的阻力。但其复杂的表面形状不利于工程实践中的应用。郭廷凯等[6]在数值研究中提出了横截面为波形的另一管桩模型，研究了波纹管桩对升阻力系数的抑制效果。本文针对该波纹管模型，主要研究其波高对涡激振动响应特性的影响，利用CFD 技术进行绕流计算，通过分析升阻力系数及涡旋脱落特性研究波高对该波纹管结构绕流特性的影响规律。结果表明，不同波高的波纹管之间的涡激振动响应特性有着明显的区别。

1 数值建模

本文采用CFD 方法，计算二维波纹管结构的绕流特性，LEI，et al[7]研究表明如果横向边界距离圆柱中心至少8 D，则横向边界不会对全局参数的预测产生重大影响。在Gambit 软件中建立二维流体计算模型并划分网格，计算域如图1 所示，宽度设置为圆柱特征长度D 的30 倍；长度是结构模型特征长度D 的60 倍。圆柱距离左侧边界为15 D，距离右侧边界为45 D，距离上下边界为15 D，近场流域为直径10 D 的圆柱。

LEE，et al[5]，ASSI，et al[8]等对横截面沿跨度呈正弦变化的柱体的涡激振动做了大量研究，但其特有的几何结构生产成本很高，多由3 D 打印技术生产制造。本文提出一种结构简单的波纹管模型，改变普通圆柱横截面形状为波形，保证特征长度D 和波数6 不变，计算5 种不同波高Hw（0.01 D，0.02 D，0.03 D，0.04 D，0.05 D），图2 为波纹管结构示意图。

为了揭示不同波形结构的柱体对流场涡激振动的特性影响，建立各波形结构2 D 网格模型并进行数值计算。在CFD数值模拟中，计算精度和计算速度等问题与数值计算模型网格划分的疏密程度密切相关，网格离散化的精度直接影响数值计算的结果[9]。本研究使用混合型网格，为了提高计算的精度，对波纹管的近场区域使用四边形网格进行细化加密，外部区域对计算精度的影响较小，因此采用三角形网格以便于网格划分且提高计算效率。为了捕捉流动分离及尾流场中的细节问题，采用SST k-ω 近壁湍流模型，该模型要求近壁面的贴体网格需要布置在粘性底层内，使得壁面函数y+≈1。此外，对网格密度及时间步长进行测试得到了不随网格密度变化的升阻力解。对网格以及时间步进行收敛性测试，在波纹管周围划分200 个节点，即网格数量为37 792 个，计算时间步设置为0.005，在保证计算精度的同时提高计算效率。图3 为计算与网格模型，图4 为近场域网格模型，图5 为边界层网格模型。

图1 模型计算域Fig.1 The computational domain

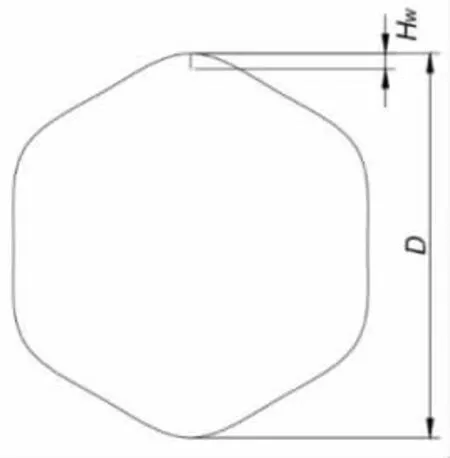
图2 波纹管结构示意图Fig.2 Structural sketch of wavy cylinders

图3 计算域网格Fig.3 Mesh generation of computational domain

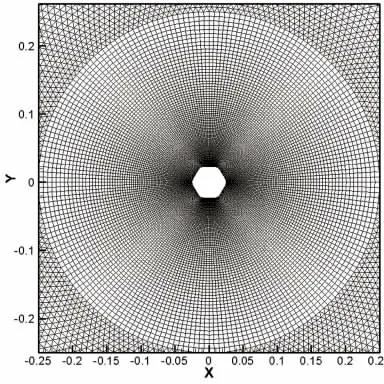
图4 近场区网格划分Fig.4 Mesh generation near the wavy cylinder

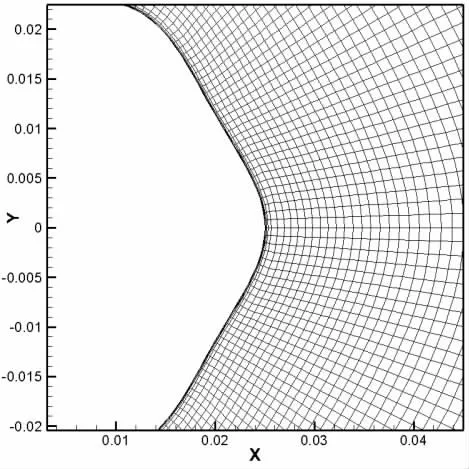
图5 边界层网格划分Fig.5 Mesh generation of boundary layer

计算流场采用Fluent 求解，压力速度耦合选用SIMPLEC 算法，压力项、动量方程、湍流动能、湍流耗散率等离散方法及瞬态项格式均采用二阶迎风格式以获得较准确的解，且绝对稳定。边界条件设置[4]：为保证流体均匀流动，右侧边界设置为速度入口边界，湍动能，耗散率；右侧边界设置为压力出口边界，静压统一设置为0，k=0、ω=0，在上下边界采用壁面边界，壁面剪切力为0；内部圆柱边界设置为无滑移固壁边界条件。

2 计算结果与分析

计算通过改变流速研究波纹管的VIV 特性[10]，计算雷诺数在5 000～6 0000 之间，计算工况如表1 所示。

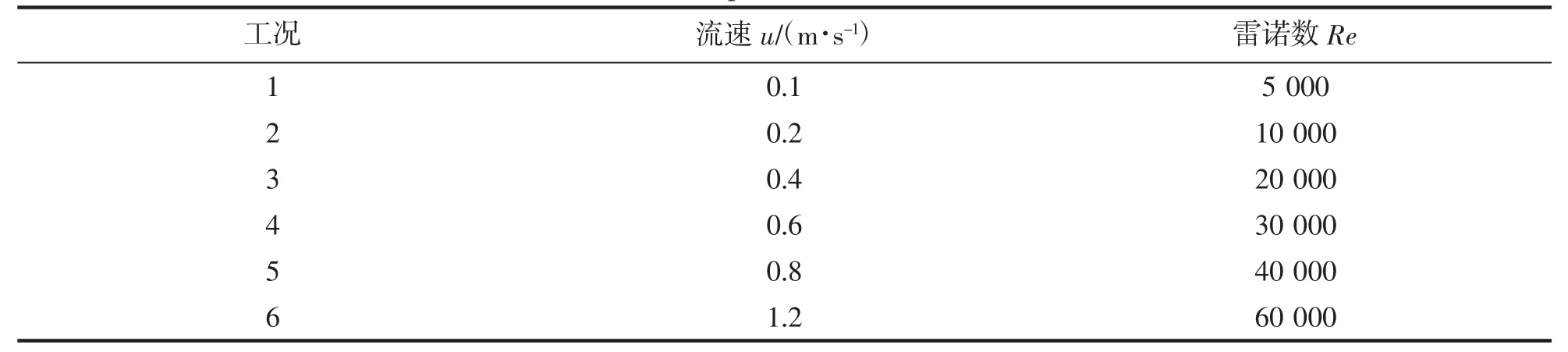
表1 计算工况Tab.1 Computational conditions

2.1 受力特性

对不同工况下的波纹管绕流特性进行研究，确定不同流速下波高对波纹管VIV 的影响特性。图6 给出了不同波高下的波纹管阻力系数均值、升力系数均方根、升力系数幅值随流速增加时的变化规律。

图6 Cd 均值、Cl 均方根、Cl 幅值随流速变化曲线Fig.6 Curves of mean Cd、rms Cl and Cl amplitude with flow velocity

波高为0.01 D 时Cd均值、Cl均方根、Cl幅值随流速增加呈现下降趋势并趋于稳定，对流速的敏感性最高；而在其他波高情况下，Cd均值随着流速增加先降低再升高再缓慢降低，而Cl均方根、Cl幅值随着流速增加先降低再升高并趋于稳定。可以看出，流速在0.4 m·s-1，是一个转折点；当流速大于0.6 m·s-1时，Cd均值、Cl均方根及幅值均变化较小且趋于稳定，对流速敏感性降低。

由于波纹管和圆柱具有明显不一样的表面形状，边界层分离点位置和可能激发的涡旋运动规律均不同，因此波纹管绕流与普通圆柱绕流[11]的升阻力变化呈现出不同的趋势。

为了更好的确定波高对结构VIV 受力特性的影响，图7 给出了不同流速下波纹管阻力系数均值、升力系数均方根、升力系数幅值随波高的变化曲线。

图7 Cd 均值、Cl 均方根、Cl 幅值随波高变化曲线Fig.7 Curves of mean Cd、rms Cl and Cl amplitude with wave height

从图中可以看出，低流速（0.1 m·s-1、0.2 m·s-1、0.4 m·s-1）与高流速（0.6 m·s-1、0.8 m·s-1、1.2 m·s-1）有着明显不同的变化趋势：当流速较低时，Cd均值、Cl均方根、Cl幅值均随着波高增大先降低再升高；当流速较高时，Cd均值、Cl均方根、Cl幅值随着波高增大先升高再降低。而流速为0.4 m·s-1的变化则表现出先升高再降低再升高的趋势。可以看出，波高为0.03 D 时为一转折点。低流速情况下时Cd均值、Cl均方根、Cl幅值均出现降低趋势，而高流速情况对应波高大于0.03 D 时则出现升高趋势。

在低流速情况下，较低波高的波纹管Cl均方根、Cl幅值均低于较高波高，横向受力较小；而高流速情况下，较大波高的波纹管Cd均值、Cl均方根、Cl幅值均小于较低波高的情况，此时较大波高的波纹管对顺流向横流向VIV 响应受力较小。

图8 所示的来流速度为0.4 m·s-1时不同波高波纹管与轨迹曲线，两者之间的轨迹均呈现出“右8”形，与黄色三角轨迹所示的普通圆柱具有相似特征。这一轨迹形状是由于流体经过波形管后段产生回流使得波纹管上下侧产生压力差，从而引起脉动升力和脉动拖曳力，脉动升力的周期为脉动拖曳力的两倍。图中可以明显看出，波纹管上的与轨迹曲线较圆柱体仅限于局部区域，力波动相对于普通圆柱体有着明显的减弱。

2.2 频域特征

圆柱体涡激受力与尾流中的涡旋脱落有关，为了更好的确定涡脱频率，描述普通立管或波形立管流动的涡激振动特征，对柱体涡激受力进行傅里叶计算获得不同波高下的波纹管在不同流速时的振动频率。图9、图10 给出了涡脱频率分别随流速、波高的变化曲线。

图9 表明为波纹管涡脱频率随着流速增加而增加，涡脱频率与流速变化有着近似的线性关系，这与普通圆柱具有相似的频率变化特性；图10 表明，当波高0.05 D 时涡脱频率出现了降低的趋势。上述结果表明在高流速较大波高这一组合工况时对VIV 有抑制效果。

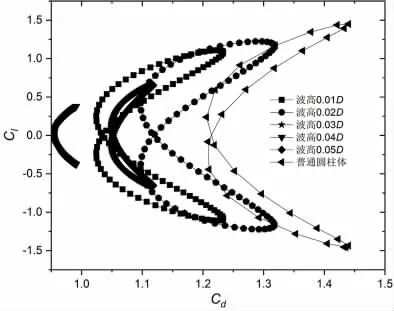
图8 u=0.4 m·s-1 不同波高波纹管Cd 与Cl 轨迹曲线Fig.8 Cd and Cl trajectory curves with different wave heights，u=0.4 m·s-1

图9 涡脱频率随流速变化曲线Fig.9 Curves of fs with flow velocity

图10 涡脱频率随波高变化曲线Fig.10 Curves of fs with wave heights

表2 不同工况下的斯托哈儿数Tab.2 Statistics of Strouhal number under different conditions

GUPTA，et al[12]在论文研究指出St 数与Re 的大小相关，且在亚临界区域（Re≈3×102～3×105），圆柱体St 数均稳定在在0.2 附近。表2 所示当波高大于0.04 D 时，雷诺数大于20 000 这一范围St 数较大，说明在此区域内尾涡的脱落是开始不再规则有序，而当波高为0.05 D 时则又恢复了稳定有序地尾涡脱落形式。因此波纹管结构的斯托哈尔数随着波高的改变而变化。

3 总结

本文提出了一种波纹型柱体模型，开展不同波高对波纹管涡激振动特性问题的数值仿真研究。计算中通过改变流速来探讨波高对波纹管VIV 响应特性的影响规律，包括受力特性、频域特征等。

在雷诺数5 000～6 0000 的范围内，分析比较了不同波纹管结构的涡激振动特性。研究表明，波高为0.05 D 时Cd均值、Cl均方根、Cl幅值随流速增加呈现下降趋势并趋于稳定，对流速的敏感性最高；对于其他波高，当流速大于0.6 m·s-1时，Cl均方根及幅值均变化较小趋于稳定，对流速敏感性降低。不同波高波纹管绕流与圆柱绕流随流速升阻力变化均呈现出不同的趋势；在低流速情况下，较低波高的波纹管Cl均方根、Cl幅值均低于较高波高，横向受力较小；而高流速情况下，较大波高的波纹管Cd均值、Cl均方根、Cl幅值均小于较低波高的情况，此时较大波高的波纹管对顺流向横流向VIV 响应受力较小；涡脱频率与流速变化有着近似的线性关系；波高小于等于0.04 D，雷诺数大于20 000 这一范围St 数较大，说明在此区域内尾涡的脱落是开始不再规则有序。而在较大波高0.05 D 时则又恢复了稳定有序地尾涡脱落形式。