深水网箱的单锚腿系泊系统动力特性分析研究

王绍敏，陶启友，袁太平，黄小华，胡 昱，刘海阳

（中国水产科学研究院南海水产研究所，农业部外海渔业开发重点实验室，广东省网箱工程技术研究中心，广东广州 510300）

深水网箱养殖是近二十年来发展较快且较好的水产养殖产业。目前网箱的系泊主要采用辐射式多点系泊方式，但该系泊方式对施工要求较高，所以对缺乏专业施工装备的养殖者而言存在较高难度。在既定海域中尽可能多的布置网箱是业者追求高经济利润的手段之一，而辐射式多点系泊方式由于安全系泊半径的要求往往会占用较多海域，且水深越深海域占用越大，这些现实问题与矛盾在一定程度上制约了网箱养殖走向深远海。

单点系泊系统主要相对多点系泊系统而言，是实现海洋结构物仅以结构物上某一处或区域为系泊位置而实现锚固的系泊系统。单点系泊系统不仅具备投资小、易于回收、施工简便、工期较短，抵抗恶劣环境优势明显等诸多优点，而且由于其特殊的风标效应给养殖行为带来的生态优势[1]，近些年来引起了业内相关学者的关注。HUANG Chaicheng，et al[2]研究了各种环境载荷条件下单点系泊重力式网箱的结构强度及可靠性；DECEW，et al[3]分析了一种单点系泊的梯形网箱在纯流作用下的动力特性；SHAINEE，et al[4]和XU Tiaojian，et al[5]计算了规则波和水流作用下单点系泊网箱的自潜特性。不难发现，相关研究大多聚焦于养殖网箱本身，而单点系泊系统本体的研究尚未涉及。

在单点系泊系统中，单锚腿系泊系统，简称SALM （single anchor leg mooring）系统是应用较广泛的一类，因此本文依据产业特点专门设计一种单锚腿单点系泊系统，对之展开力学特性研究，并对其与网箱建立时域耦合分析模型，分别研究锚泊线顶端激励、浮筒与底部重量的运动响应，以期为单点系泊深远海网箱产业发展提供科学指导和参考依据。

1 单锚腿系泊系统设计

养殖行为过程中对占海面积小的要求，最终便是要求系泊网箱离开平衡位置的距离短、系泊系统的系泊半径小或者尽可能长的以海底卧链形式呈现。系泊物在水平面偏移量与系泊系统的系泊刚度密切相关，系泊系统的水平刚度主要提供网箱水平方向的恢复力，该恢复力主要通过系泊腿的悬链线自重和预张力提供；而在垂直方向上，恢复力主要依赖于系统顶端浮体自身浮力提供，传统网箱的系泊便是直接将系泊缆索与网箱浮管连接，由浮管的浮力提供垂向恢复力。

为了高效利用海域，本文借鉴软钢臂系泊系统的工作原理，[W 用7]结合利用单锚腿系泊系统中配重缓冲系统与浮筒缓冲系统的各自特点，设计一种符合养殖行业的新型、简易且施工方便的单锚腿系泊装置，设计图如图1 所示。系统由水面浮筒、海床重量1、海床重量2 和船锚通过中间锚链连接组成，其工作原理为：系统工作过程中，网箱因为受到日常环境合力发生位移带动水面浮筒离开初始平衡位置“Ⅰ”，平衡于新位置“Ⅱ”处，此时的状态为钢链B 发生偏转、浮筒吃水增加、重量1 未离开海床；当极限海况情况发生，网箱遭受更高的环境载荷时进一步带动浮筒从位置“Ⅱ”处平衡于位置“Ⅲ”处，此时的状态为钢链B进一步发生偏转、浮筒吃水更大、重量1 离开海床、钢链C 发生偏转但重量2 依旧保持于海床上，维持重量2 持续在海床上的状态以防止对锚产生上拔力而走锚，达到网箱于指定点安全系泊的目的。通过合理的尺寸设计优化，满足水面浮筒与海床重块之间形成一个“柔性缓冲臂”[6]并使系泊系统自带两级刚度，最终实现养殖网箱于各环境条件情况下的系泊要求。

图1 单锚腿系泊系统示意图Fig.1 Schematic diagram of single anchor leg mooring system

2 系泊系统计算

2.1 计算理论

按三维势流理论，流场存在不定常速度势φ，可分解为入射势φI、绕射势φD及辐射势φR，对于系泊系统的浮筒在静水自由面上进行六自由度摇荡时，φ 满足以下定解条件[7]：

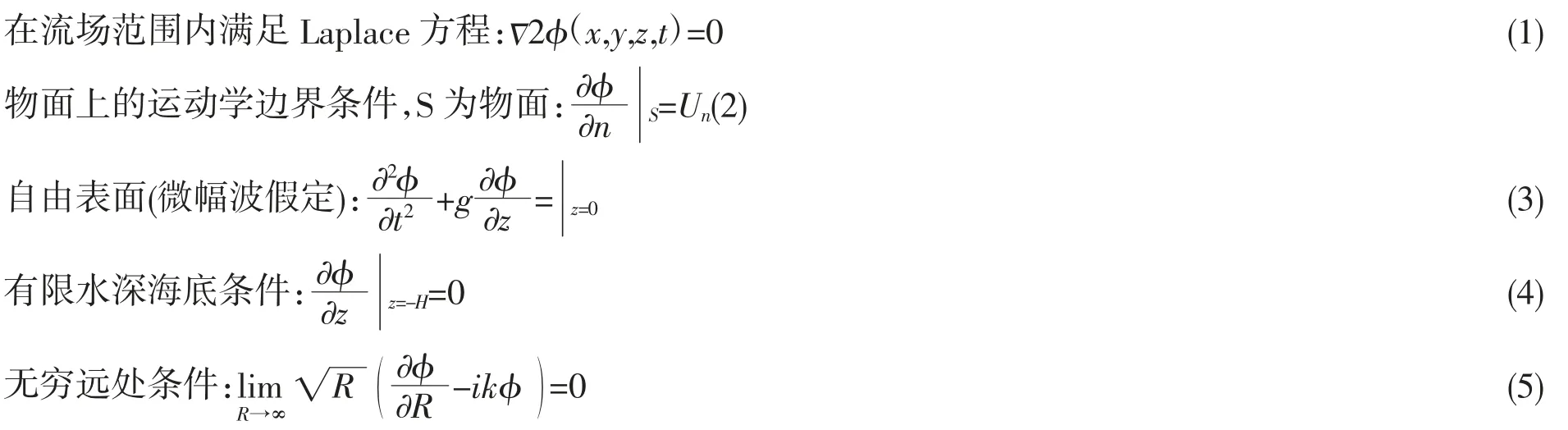
采用GREEN 函数法[8-9]，将上述定解条件下的控制方程变换成边界上的积分方程来进行求解。求得速度势φ 后依据Bernoulli 方程，对流场的压力分布进行求解，即可得到浮筒受到的总体流体作用力，包括波浪激振力、流体反作用力及回复力。其中，波浪激振力由入射势φI和绕射势φD引起的压力积分求得，流体反作用力则由辐射势φR所引起的压力积分得出。由于现有网箱使用海域的水深大多还未超出20 m，为了有效计及浮筒的浅水效应，使用远场法对由速度势引起的二次传递函数QTF（quadratic transfer function）展开计算，求解全QTF 矩阵，以获得浮筒的二阶波浪力。

在分析锚泊线的运动响应时，把锚泊线假定为完全挠性构件，选取单位长度锚泊线，其运动控制方程采用Berteaux[10]提出的公式：

式中：m 为单位长度钢链的质量；V 为钢链速度矢量；T 为钢链中产生的张力；G 为单位长度钢链的重力；Ff为单位长度钢链在受到的流场作用力，流场对钢链的作用力主要由惯性力和粘性力两部分组成，采用Morison 公式计算。

式中，Ff为流场作用力；Δ 为钢链排开流体的质量；af为流体的绝对加速度；Ca为附加质量系数；ar为流体的相对加速度；ρ 为流体密度；Vr为流体的相对速度；Cd为钢链粘性力系数；A 为钢链的迎流面积。

采用快速Fourier 变换，产生波浪激励的时间序列，将已经确定的波浪谱转化到时间域，通过卷积积分的方式以求得相应的一阶和二阶波浪载荷的时间历程，然后采用数值积分求解时域内的运动微分方程，得到浮筒六自由度运动时历。单锚腿系泊系统时域耦合运动基本方程[7，11]为：

2.2 系统刚度计算与实测验证

系泊系统海上实测地点位于我国南海北部放鸡岛海域西侧，平潮水深12.7 m，平均潮差2 m，数据采集系统为100 kN 量程的水密高灵敏度拉力传感器与配套采集系统，由南京凯基特电气有限公司生产，型号为KNW301-PG，精度0.1 kN。传感器设置于浮筒与钢链B 的连接处，采用水面干电池供电，干电池由太阳能板充电，与数据采集系统一起设置于浮筒顶部。系泊系统主要构成部件参数为：水面轻质浮筒（聚脲塑料）体积4.5 m3，底面直径1.5 m，高2.4 m，自重400 kg，；重量1 自重5 760 kg；重量2 自重1 500 kg；锚为大抓力船锚，自重500 kg；钢链B 长11 m，钢链C 长5 m，钢链D 长10 m，钢链B、C 和D 均选用链径φ22 mm的AM2 级有档锚链，破断负荷240 kN。2017 年12 月30 日，等待平潮、微风、有义波高约0.5 m 的天气窗口时展开实测。实测环节，由渔船展开拖带作业实现浮筒沿X 向离开平衡位置进而在钢链B 中产生不同张力，由传感器测量并记录，以获得系泊系统的实测数据。海上实测的时候正处于平潮向落潮发展过程中，而系泊系统为按平潮水位设计，因此低潮位时匀质浮筒会发生歪倒，给实测与数据采集造成困难，同时距离小于2 m 浮筒离开平衡位置过小在风浪中的摇摆频率高，距离大于5 m 已经超出拖带渔船的拖带能力，因此实际获得的数据是水平位移为2～5 m 范围内所对应钢链B 顶端的张力数据。

对实际海域布置的系泊系统水平刚度进行了数值计算，计算结果与实测数据比对情况如图2 所示。实测数据相比于数值计算数据偏小，这是因为：1）可能存在平潮水位水深的实际测量值不够精确，最终选择的12.7 m 大于实际水深；2）系统是以平潮水位设计，实测处于潮水回落时刻，测试海域水深逐渐减小，浮筒吃水减小导致浮筒离开设计的水平平衡位置时，钢链张力值偏小。但是，数值模拟结果和实测值最大相对误差可以接受，如，当浮筒离开平衡位置4.7m 时，锚链张力实测统计平均值为17.9 kN，数值计算理论值为20.75 kN，相对误差为13.75%；同时数值计算值变化趋势与实测值变化趋势基本一致，可认为本研究数值方法具备一定合理性和精度。

图2 水平刚度曲线Fig.2 Horizontal stiffness curves

3 案例数值计算

3.1 计算模型与参数

本研究以文献[12]中的NACA0030 对称翼形网箱为系泊对象，将本文设计的系泊系统与其耦合并展开计算，研究系泊系统钢链B 顶部的张力、浮筒沿环境载荷方向位移、重量1 的垂向位移变化特性关系。依据图1，针对平潮水深为D=15 m、潮差2 m 的养殖海域完善系泊系统的主要构成部件参数，分别为：匀质浮筒底面直径1.5 m，高2.4 m，自重400 kg，初始位置（-24，0，0）；钢链B 长14 m，钢链C 长5 m，钢链D长10 m，钢链均为链径φ 22 mm 的AM2 级有档锚链，破断负荷240 kN；重量1 自重5 760 kg，体积2.3 m3，初始位置（-24，0，-D），重量2 自重1 500 kg，体积0.2 m3；船锚为大抓力锚，自重500 kg；海床为水平、泥沙底质，法向刚度为100 kN/m/m2；耦合系统坐标原点为处于海面的网箱浮管系泊点处，环境载荷沿X 轴正向，养殖海域的环境条件如表1 所示。

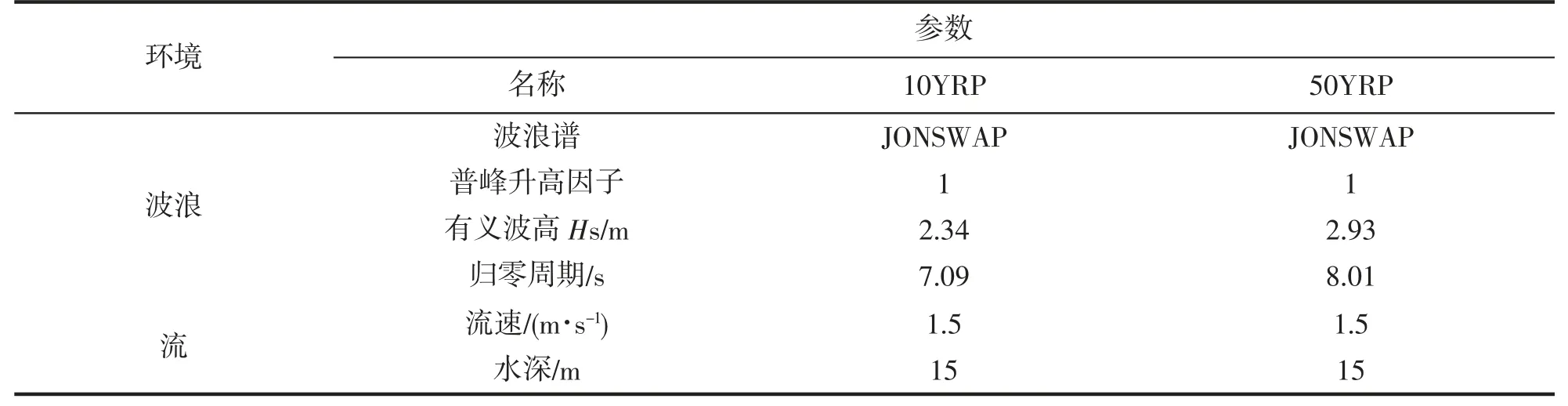
表1 养殖海域环境条件Tab.1 Environmental conditions in cultured sea areas

3.2 计算结果及分析

由于海水潮汐特性会使得水深产生变化，在一个潮时会出现3 个水深：满朝水深、平潮水深和干潮水深，如图1 所示，不同水深情况下钢链B 的张力情况会发生变化；钢链B 的张力除与水深相关，还与其长度有一定关联，浮筒的移动距离与其受力和链长有关联，也会影响重量1 的受力与运动，因此从这些方面展开比较计算，明确环境条件、水深、链长与张力、浮筒位移与重量1 位移之间的关系。

3.2.1 张力与水深、链长的关系

2 种海况与不同组合情况下钢链B 的张力时历曲线如图3 所示，通过图3a）曲线可知，10YRP 海况下张力极值约50 kN，在同等链长情况下，水深越小，张力最大值相反较大，而同等水深情况下，张力最大值随链长增加而减小；通过图3b）曲线可知，50YRP 海况下钢链B 顶端张力极值约55 kN，同等链长情况下，3种水深下张力最大值较为接近，而水深相同链长不同的4 种情况下的张力最大值亦比较接近。

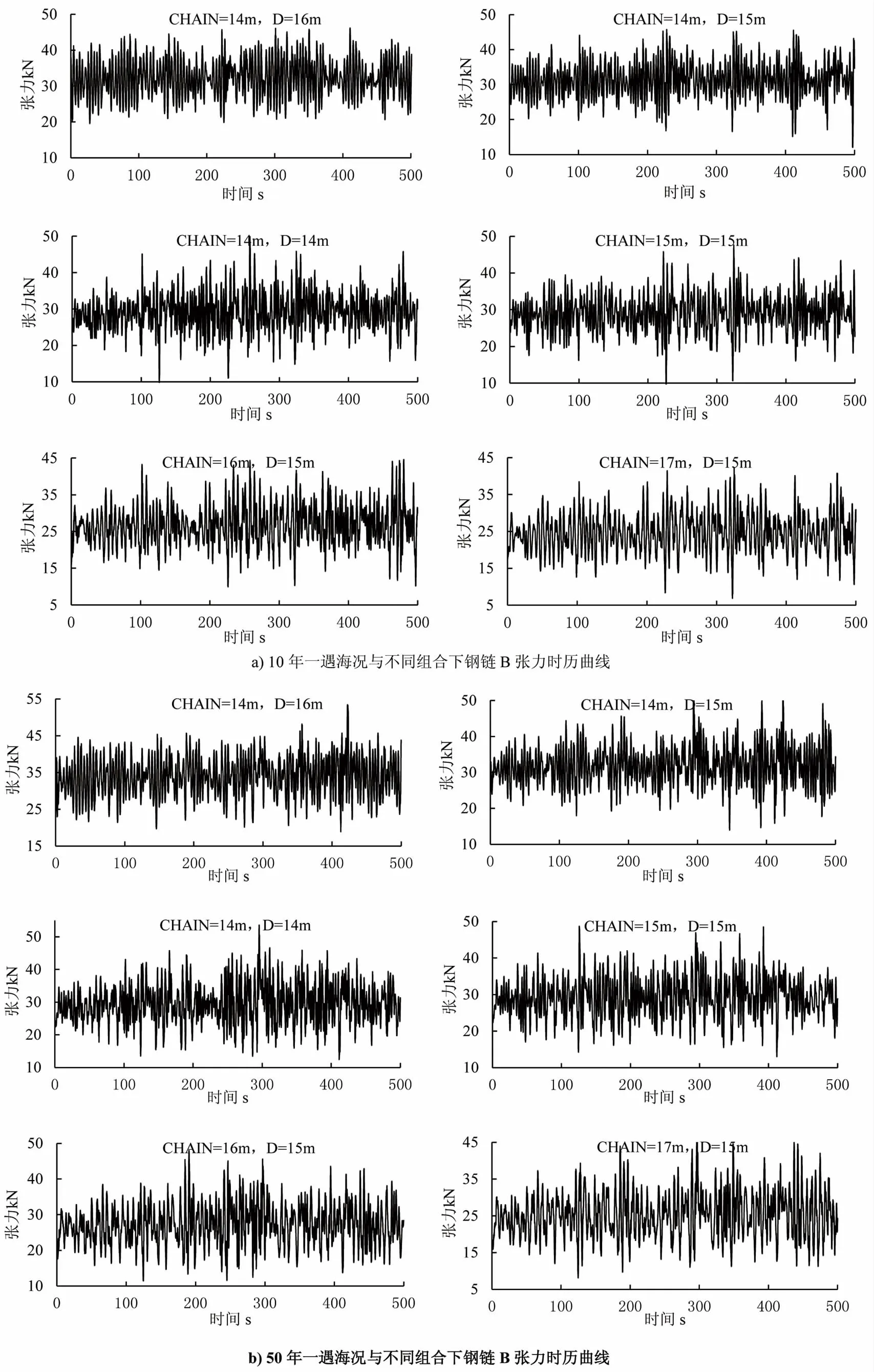
图3 2 种海况与不同组合下钢链B 张力时历曲线Fig.3 Time history of steel chain B tension under two sea conditions with different chain lengths and water depths

对张力时历曲线进行统计分析，分析结果如表2 所示。在链长均为14 m 时，张力的均值、最小值均随着水深变深而变大，而最大值基本呈现减小趋势，除10YRP、D=16 m 情况下的张力最大值46.149 kN 相比较于15 m 水深时的45.733 kN 略有变大，且50YRP 海况下3 个张力最大值非常接近；而当水深一定，张力均值与极值随着链长的增加而逐步减小，除10YRP 海况下，链长15 m 的张力最大值相比14 m 略有增加后，再次随着链长增加而减小；通过张力的总均方差的变化趋势：水深一定，张力总均方差随链长的增加而增加，说明系泊系统的柔性缓冲臂在各海况情况中处于受力张紧状态下较为稳定；链长一定，张力总均方差随水深增加呈现先降后升的趋势，说明在平潮水深15 m 情况下张力值振荡较为平缓。

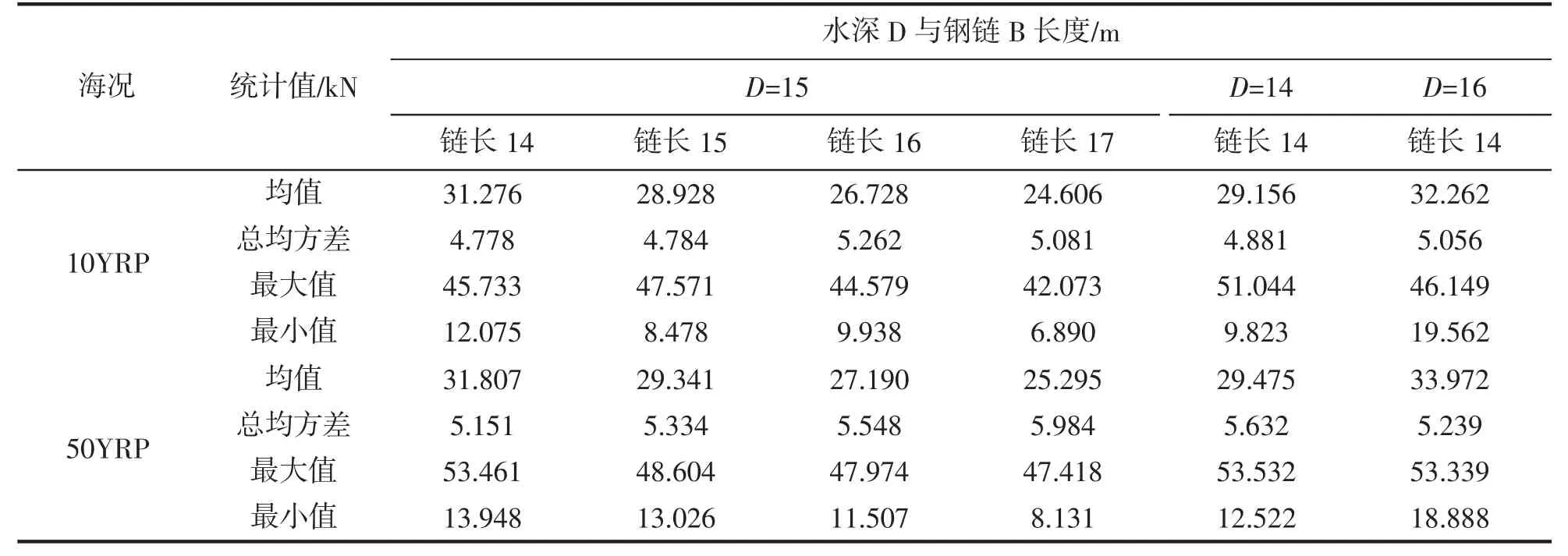
表2 张力统计分析结果Tab.2 Statistical results of tension

通过张力谱的对比，如图4、图5 所示。通过图4a）可知，10YRP 海况、链长14 m 情况下，随着水深的逐渐增加，张力谱从起初的频谱宽0～0.4 Hz 范围且无明显谱峰的情况，逐渐变化为带宽变窄至0.24～0.32 Hz且谱峰峰值变大，直至水深16 m 时的频谱带宽进一步变窄为0.2～0.25 Hz、谱峰峰值变大约为550 kN2/Hz。通过图5a）可知，50YRP 海况、链长14 m 情况下，随着水深的逐渐增加，频谱曲线的变化情况与图4a）有一定的区别。张力谱在水深14 m 时的频谱带宽依旧较宽为0～0.5 Hz，但在0～0.2 Hz 范围内存在较为明显的谱峰，峰值约200 kN2/Hz；水深15 m 时，谱峰峰值向高频区域0.21～0.3 Hz 偏移，峰值略有变大，约240 kN2/Hz，其它频率范围对应的峰值开始减小；水深16 m 时，谱峰峰值带宽区域向低频0.2～0.28 Hz 区域偏移，峰值再次变大，约307 kN2/Hz，其它频率范围对应值在15 m 基础上略有减小。说明钢链长度一定，钢链B 中的张力由低频与波频载荷共同形成，而随着水深增加，低频部分逐渐降低，波频分布逐渐变窄；同时水深15 m 和16 m 两种情况下曲线在0～0.18 Hz 和0.33～0.6 Hz 两个范围内非常接近，因此这两个频率范围内的载荷的影响基本趋于稳定，但其影响不能忽略。

对比图4b）、图5b）可知，随着链长增加，张力谱曲线的频谱峰值先向高频区域发展且低频区域的谱值变大，而后峰值再次向低频区域发展，且峰值逐渐变大，高频区域的谱值逐渐变小。

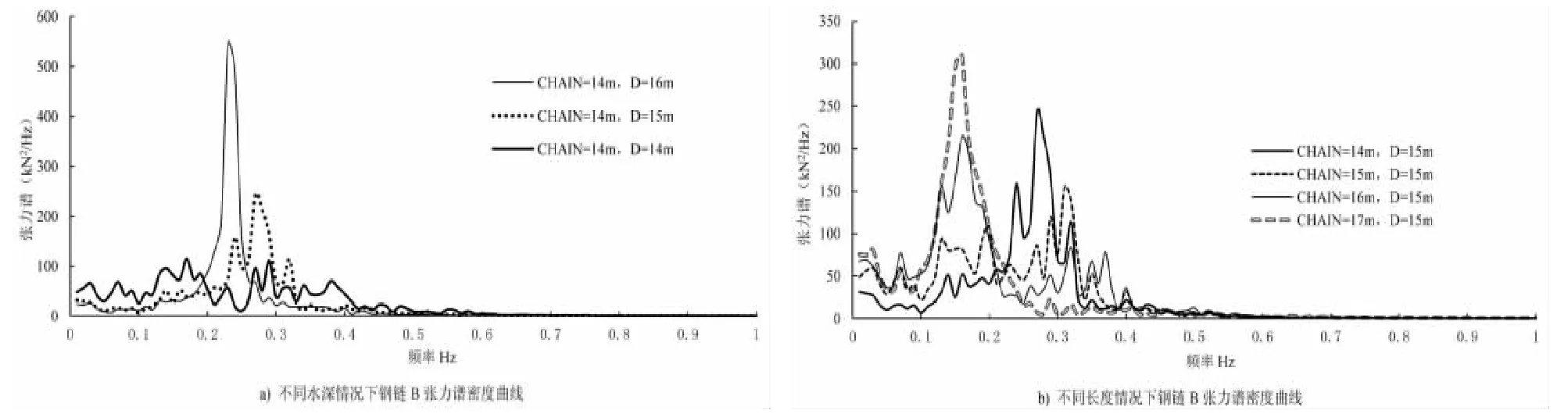
图4 10 年一遇海况与不同组合下钢链B 张力谱密度曲线Fig.4 Tension spectral density curves of steel chain B under 10 YRP sea conditions with different water depths and chain lengths

图5 50 年一遇海况与不同组合下钢链B 张力谱密度曲线Fig.5 Tension spectral density curves of steel chain B under 50 YRP sea conditions with different water depths and chain lengths

3.2.2 浮筒、重量1 运动与水深、链长的关系

浮筒离开初始位置距离的远近直接关系系泊网箱离开初始位置的远近，也是对网箱占用海域面积的直接影响因素。两个海况下浮筒的离开初始位置的情况如图6 所示，结合统计分析结果（表3）可知，设计状态下，随着水深从14 m 增加到16 m，浮筒离开初始位置的距离逐渐减小，这是因为钢链B 中的张力随水深增加逐渐变大，其张力水平方向的分力也变大限制了浮筒离开平衡位置；且均值、极值与均方差均随水深增加而减小。同时，统计结果显示，水深一定情况下，浮筒位移的均值、总均方差与极值均体现出了较明显的规律，随着钢链长度的增加，浮筒离开初始位置的距离亦逐渐增加，链长17 m 时达到最大，约12.6 m。

图6 2 种海况与不同组合下浮筒位移时历曲线Fig.6 Time history of buoy's displacement under two sea conditions with different water depths and chain lengths

表3 浮筒离开初始位置统计分析结果Tab.3 Statistical results of the buoy leaving its initial position

重量1 在遭受钢链B 张力的垂向分力时可能会导致其发生垂向运动而离开海床，该垂向运动的幅度大小直接关系系泊系统中重量2 的受力与运动。通过对重量1 垂向位移时历曲线的统计分析，结果如表4所示，链长一定，水深逐渐变深的情况下，两个海况下重量1 离开海床的距离逐渐变大，最小值为水深14 m 时的14-12.143=1.857 m，最大值为水深16 m 时的16-12.434=3.566 m，且均值、总方差与最大值均为递增趋势，这是因为钢链B 的张力逐渐增大并导致施加于重量1 的作用力增加而引起；当水深一定，链长逐渐变大的过程中，重量1 离开海床的距离也变小，最大值为链长14 m 时的15-12.187=2.813 m，最小值为链长17 m 时的15-13.799=1.201 m，且均值、总方差与最大值均为递减趋势。

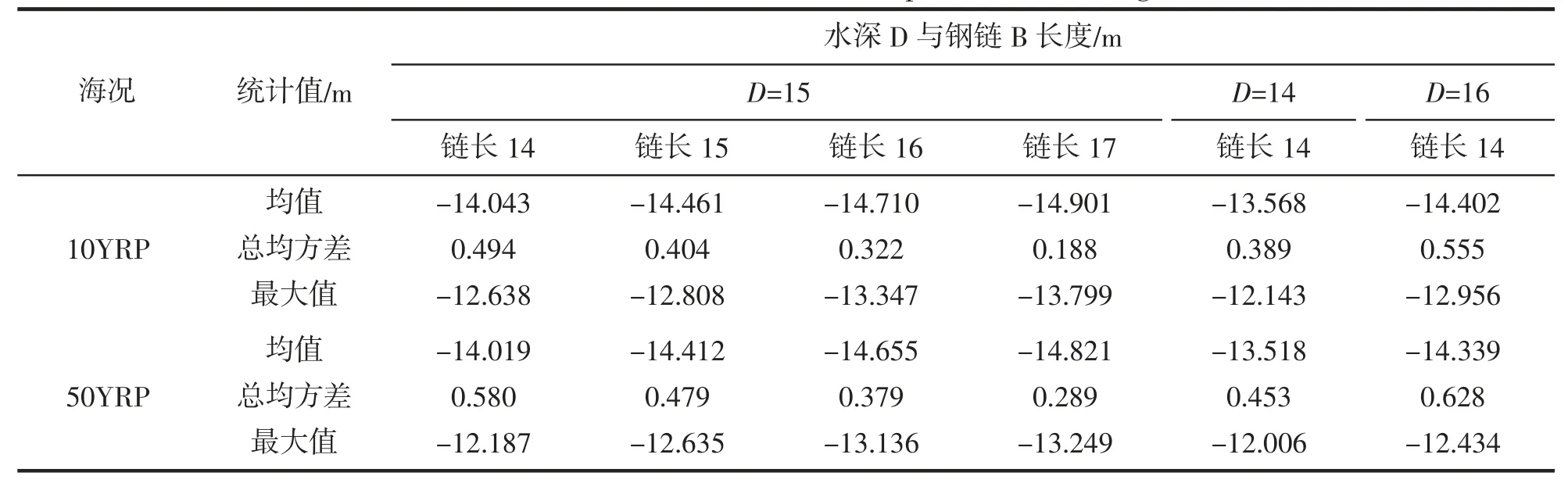
表4 重量1 垂向位移的统计分析结果Tab.4 Statistical results of vertical displacement of weight 1

3.2.3 系泊系统的安全与适用情况分析

10YRP 和50YRP 的两种海况钢链B 内的张力最大值产生于水深14 m、链长14 m 的组合工况中，其值53.532 kN，如表2 所示，由于钢链的破断负荷为240 kN，安全系数可达4.48，系统具备足够的安全性。在链长14 m 情况下，浮筒偏移最大值为水深14 m 时的-14.554 m，如表2，可通过计算知其X 向偏移距离不到10 m，而此时重量1 的离开海床的垂向距离最大为3.566 m，此组合情况下重量2 持续位于海床（限于篇幅，文章并未罗列），确保了钢链C 作为海床卧链防止产生上拔力而走锚。因此综合评判设计状态下的系泊系统，虽然钢链B 中的张力大于链长增加的组合，但仍旧足够安全，且从养殖海域的节约程度而言具有更好的收益，符合当下养殖现状的需求。

总体而言，本文设计的系泊系统，浮筒、重量1、重量2 的外形和尺度选择和钢链B 乃至钢链C 的长度对系统安全有效发挥作用比较重要，其相互间的影响亦比较复杂，特别是水面浮筒的大小和外形会直接关系到钢链B 中张力，如3.2.1 节有关分析，而且其摇荡运动与系统内的受力和寿命都密切相关。鉴于系统水面浮筒波频与低频运动响应对系统整体的重要影响，在锚泊系统的设计中还需要进行更加细致的分析。

4 结论

本文在充分掌握现有养殖网箱系泊系统现状的基础上，结合软钢臂系泊系统的特点，设计出一种自带“柔性缓冲臂”与两级刚度的单锚腿单点系泊系统服务于网箱养殖。通过对系统设计状态下不同水深以及改变系统钢链B 长度情况下各部件的受力与位移变化规律进行计算，分析了浮筒大小和位置对锚泊线阻尼特性的影响，可以得到以下结论：

（1）链长一定情况下，钢链B 中的张力均值虽然随水深增加而增加，但最大值却随水深的增加而减小；水深一定时，钢链B 中张力均值和最大值基本呈现随链长的增加而减小的趋势；各组合下钢链B 的张力均由低频与波频共同作用产生。

（2）水面浮筒离开平衡位置距离随钢链B 长度的增加而增加，随水深的减小而增加；而海床重量1 的垂向位移距离随水深的增加而变大，随链长的增加而减小。

（3）所设计的系泊系统在两种海况下具有较高的安全系数，且不会出现因为锚点的上拔力而走锚的现象，同时浮筒的偏移距离也最小，具备较高的安全性与产业适用性。

（4）由于所有的研究过程中均未对浮筒自身的六自由度响应展开细致分析，其作为该系泊系统的核心部件，自身的运动响应会关乎到水下与其连接部件的设计与安全寿命；同时由于钢链B 中会持续存在一定的预张力，亦会对其连接部件提出更高的要求，建议在后续研究中就两方面展开细致研究。

（5）该系泊系统下，养殖海域的往复流现象会引起网箱发生180°的旋转，若此刻遭遇同向极限海况，还需对系泊系统在本文基础上进行补充与完善，可参照文献[13]中的形式，并据此进行有关研究。