燃气挤压器式辅助动力源起竖装置建模及性能

任玉亮， 高钦和， 周伟， 冯江涛， 刘志浩

(1.火箭军工程大学 导弹工程学院，陕西，西安 710025；2.中国人民解放军96796部队，宁夏，银川 750000)

当前，车载导弹发射系统普遍采用传统液压起竖方式，存在着起竖时间长，装机功率大等问题[1]. 实现导弹快速起竖，探索新型起竖液压动力源成为一个新的研究方向. 液压系统通常采用液压泵作为动力元件. 孙通[2]提出一种基于燃气助力的混合驱动起竖方案，将燃气发生器驱动的燃气作动筒作用于导弹起竖臂末端，完成初始阶段起竖任务，而后采用液压驱动完成后续起竖工作，同样可以实现快速起竖. 由此可见，这种以火药爆炸产生燃气为动力源的驱动装置不仅具有瞬时输出高功率的特性，而且体积小、重量轻，非常适合于空间有限的车载导弹武器系统的起竖装备[3]，具有较高的理论研究价值和广泛的工程应用前景.

目前，在导弹气体挤压式液压动力源起竖领域，已有部分学者开展了相关研究. 张春峰[4]提出一种基于液压蓄能器式辅助动力源的起竖系统，建立了系统的AMESim仿真模型，设计搭建了起竖系统测试试验平台，开展了试验研究，验证了起竖方案的可行性. 冯江涛等[5]研究了基于多级缸执行机构的液压蓄能器起竖方案，建立了起竖系统的仿真模型，针对液压蓄能器初始能量损耗大，效率不高的问题，提出采用高压气瓶驱动方案的分段控制策略，前期采用气体控制提高能量利用率，后期采用液体控制实现快速制动，并进行了试验验证. 邵亚军等[6]提出一种燃气液压混合驱动起竖方案，给出了燃气驱动装置的简化结构，建立了系统的动力学模型，通过遗传算法优化确定了火药结构参数，给出了优化后的起竖速度曲线，可在22.3 s内实现快速起竖，在燃气挤压式起竖方面进行了初步的探索和尝试. 但是，燃气爆炸装置是一个多参数耦合的强非线性系统，且这种燃气挤压式起竖装置中同时存在燃气、油液和机械结构，属于典型的多物理耦合系统，模型的完备性和正确性对研究结果有重要影响. 文献[6]在建模过程中进行了大量的假设和简化处理，但未对模型的合理性进行验证[7-8]. 纵观已有文献，对燃气挤压式起竖装置的研究比较少，已有研究多集中于起竖方案设计、建模和优化，但方案的有效性和模型的正确性均缺乏试验验证.

本文提出一种新型燃气挤压器式辅助动力源快速起竖方案，在建模过程中对文献[6]的建模方法做出改进，考虑液压系统实际结构形式，建立包含液压系统所有元件在内的起竖装置的气、液、机多物理系统耦合数学模型. 在Matlab/Simulink和AMESim中分别建立相关元件仿真模型，实现Simulink/AMESim联合仿真，并通过原理样机试验验证燃气挤压器仿真模型的有效性. 研究了起竖系统的快速性和功率特性，并与传统泵式液压系统进行了对比. 本文提出的起竖方案可大幅提高起竖速度，降低系统装机功率，建立的理论模型及获得的仿真结果可为快速起竖系统的研究提供参考.

1 燃气挤压器式辅助动力源起竖装置结构和原理

1.1 结构组成

燃气挤压器式辅助动力源起竖装置，其原理如图1所示. 在传统液压起竖装置液压动力源的旁路，再并联一路燃气挤压器动力源. 新系统由液压主动力源和燃气辅助动力源两部分组成. 液压主动力源由电机、定量泵、比例溢流阀、比例方向阀和平衡阀组成. 燃气挤压器辅助动力源，其结构示意图如图2所示. 主要由燃气发生器和挤压式油箱两部分组成. 燃气发生器内含固体装药，燃烧产生燃气. 挤压式油箱由内部活塞分隔为燃气腔和油液腔两部分. 其中，燃气腔一侧通过法兰盘与燃气发生器喷管相连，油液腔一侧设置出油口，通过液压阀块与电磁开关阀连接.

1.2 工作原理

燃气挤压器式辅助动力源起竖装置的工作过程分为2个阶段.

① 燃气挤压器供油阶段.

系统起竖前，电磁开关阀8.1和8.2打开，比例方向阀6关闭. 燃气发生器点火装置启动，固体装药迅速燃烧产生大量燃气，经喷管进入挤压式油箱的燃气腔，并通过推力活塞挤压油液腔的油液，当油液压力达到负载启动压力后，燃气膨胀做功，推动活塞运动，油液快速释放，经电磁开关阀8.1进入液压缸无杆腔，推动导弹快速起竖，有杆腔油液经电磁开关阀8.2回油箱. 在此期间，比例溢流阀5设定较低开启压力，定量泵2保持溢流状态.

② 液压泵源供油阶段.

燃气挤压器工作结束后，比例溢流阀5调定压力切换至系统最高压力. 同时，电磁开关阀8.1和8.2关闭，比例方向阀6开启，并调节系统速度，液压主动力源继续推动导弹起竖至90°，实现起竖臂位置精确停靠.

2 燃气挤压器式辅助动力源起竖装置数学模型

2.1 燃气发生器内弹道数学模型

2.1.1基本假设

燃气发生器内部装药燃烧过程比较复杂，为简化问题，本文作以下基本假设[9]：

①燃烧为稳定燃烧，同时忽略点火过程；②燃气在燃烧室和燃气腔的流动均为零维流动，在喷管内部流动为一维准定常等熵流动；③燃气的成分和物理化学性质固定不变，燃气热力学参数均为常量；④燃气视为理想气体；⑤燃烧室热力学过程为绝热过程.

2.1.2燃烧室控制方程

① 装药燃烧方程.

根据固体火药燃烧理论，可知

(1)

式中：μ为燃速，服从指数变化规律；P1为燃烧室压力；a为燃速系数；n为压力指数；Lb为已燃装药长度；Lp为装药总长度.

② 质量守恒方程.

燃烧室内装药的燃烧，一方面随着装药燃烧不断生成燃气，另一方面通过喷管持续向燃气腔注入燃气. 根据质量守恒定律[10]，可得

(2)

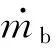
燃气质量生成速率：

(3)

式中：ρp为装药密度；Sb为燃烧面积.

燃气体积变化率：

dV1/dt=Sbμ.

(4)

③ 能量守恒方程.

燃烧室内装药燃烧可视为绝热过程，根据能量守恒原理，可得

(5)

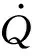
燃烧产生能量：

(6)

式中：ε为燃烧效率；cp为燃气比定压热容；Tp为燃温.

为使燃烧室方程组封闭，补充气体状态方程，可得

P1V1=m1RT1,

(7)

式中R为燃气气体常数.

2.1.3喷管质量流量和热焓注入率控制方程为

流经喷管的燃气有亚声速和声速两种流动情况，喷管质量流量方程为[11]：

(8)

式中：φ为流量修正系数；k为燃气绝热指数；St为喷管喉部面积；P2为燃气腔压力.

通过喷管注入燃气腔的热焓注入率为

(9)

2.2 挤压式油箱数学模型

2.2.1燃气腔控制方程

① 质量守恒方程.

燃气腔的气体变化量取决于喷管质量流量. 根据质量守恒定律，可得

(10)

式中：m2为燃气腔气体质量；ρ2为燃气腔气体密度；V2为燃气腔气体体积.

燃气体积变化率为

dV2/dt=Spvp，

(11)

式中：Sp为挤压式油箱内部活塞面积；vp为活塞运动速度.

② 能量守恒方程.

流入燃气腔的燃气膨胀做功，根据开口系统热力学第一定律，可得

(12)

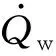
(13)

燃气膨胀对外做功，可得

(14)

同样，为使燃气腔方程组封闭，添加气体状态方程

P2V2=m2RT2.

(15)

2.2.2活塞运动方程

根据牛顿第二定律，可得

mpdvp/dt=P2Sp-PoSp,

(16)

vp=dxp/dt,

(17)

式中:Po为油液腔压力；mp为活塞质量；xp为活塞运动位移.

2.2.3油液腔压力控制方程

根据流体动力学理论，可得

(18)

式中：E为油液体积弹性模量；Vo为油腔体积；qV为阀口流量.

2.3 液压元件数学模型

液压系统中泵、阀和油缸的模型如下.

① 泵流量方程.

qVp=nqd-klPp,

(19)

式中：n为电机转速；qd为泵排量；kl为泄漏系数；Pp为泵输出压力.

② 阀流量方程.

(20)

式中：Cq为流量系数；Ao为阀口面积；Pf为液压缸无杆腔压力；ρo为油液密度；Ps为动力源压力；燃气动力源作用时等于Po,液压动力源作用时等于Pp.

③ 液压缸运动方程.

将液压缸容腔作为一个节点，利用节点容腔法建立压力方程，同时给出液压缸输出作用力方程，可得

(21)

(22)

F=PfAf-PbAb,

(23)

式中：F为液压缸输出作用力；Pf、Pb分别为液压缸无杆腔和有杆腔的压力；qVf、qVb分别为流入和流出无杆腔和有杆腔的流量；Af、Ab分别为无杆腔和有杆腔的面积；Vf0、Vb0分别为无杆腔和有杆腔的初始容积；x、v分别为液压缸活塞杆的位移和速度；l为液压缸行程.

2.4 起竖机构动力学模型

如图1所示，起竖机构构成三角函数关系为

2lOO1lOO2cos(θ+θ0).

(24)

液压缸推动导弹由水平状态转动至竖直状态. 根据欧拉运动方程，可得

mglO Gcos(θ+β),

(25)

式中：J为导弹转动惯量；m为导弹质量；θ为导弹转动角位移；θ0为导弹起竖初始角度；lO G为导弹重心G与转动中心O的距离；β为导弹重心与导弹底端水平位置的角度；ω为导弹转动角速度，其公式如下：

ω=dθ/dt.

(26)

起竖过程中液压缸活塞杆受到的导弹负载力Fload与起竖角位移θ的关系如图3所示. 随着液压缸的伸出，起竖角位移由0变为1.57 rad，导弹负载逐渐减小，在重心过平衡点后，变为超越负载.

3 燃气挤压器式辅助动力源起竖装置联合仿真模型

根据燃气发生器内弹道控制方程式(1)～(9)，在Matlab/Simulink环境下编写燃气发生器内弹道求解程序并利用S函数嵌入到Simulink中；根据挤压式油箱控制方程式(10)～(18)、液压元件控制方程式(19)～(23)和起竖机构运动方程式(24)～(26)，在AMESim中利用液压库、机械库和信号库构建挤压式油箱、液压元件和起竖机构仿真模型. 求解模块和仿真模型建立完成后，以Matlab/Simulink作为联合仿真主环境，将燃气发生器喷管质量流量和挤压式油箱燃气腔压力设为传递变量，利用联合仿真接口Simcenter AMESim co-Sim模块将AMESim构建的挤压式油箱、液压元件和起竖机构仿真模型与Matlab/Simulink搭建的燃气发生器内弹道求解模块进行连接，实现联合仿真.

起竖装置的主要仿真参数如表1所示.

表1 模型中的主要参数

4 联合仿真模型的试验验证

为验证燃气挤压器式起竖原理和联合仿真模型的有效性，设计搭建了原理样机. 限于试验条件，本文主要验证燃气挤压器动力源驱动液压缸活塞杆伸出过程的仿真模型，对应于第2部分中控制方程组(1)～(23)，暂未验证起竖机构的仿真模型，对应于控制方程组(24)～(26). 相应的，燃气发生器结构参数和挤压式油箱的结构参数根据实际试验装置进行了调整，具体见下文.

试验台硬件由燃气发生器、挤压式油箱、液压泵源、液压阀组、液压缸和数据采集、测量、控制系统组成. 燃气发生器体积为780 cm3，喷管喉部直径为10 mm，挤压式油箱直径为63 mm，总长度为1 m，液压管路直径为12 mm，液压缸行程为600 mm. 传感器型号和采集的信号有：使用拉线式传感器LEC-150采集液压缸活塞杆位移，使用压力传感器Asmik采集燃气腔压力，使用压力传感器CS -PT300采集油液腔压力. 测控系统硬件采用美国NI公司的PXI-1044机箱和PXI-6259采集卡，实现信号的采集、放大、滤波和输出，采用LabVIEW软件编写测控程序，完成信号的输入、输出和存储.

系统启动前，通过液压油源向挤压式油箱充油，充油完成后，系统发出指令信号切断油源；完成准备工作后，系统发出点火指令，装药开始燃烧产生燃气膨胀做功推动活塞挤压油液进入液压缸，进而推动活塞杆伸出，伸出到位后，系统完成一次试验.

将液压缸活塞杆位移的试验结果与仿真结果进行对比，如图4所示. 图中同时给出了采用文献[6]模型的计算结果. 从图中可以看出本文仿真模型得到的油缸启动时间约为0.85 s，与试验结果较为符合. 而由文献[6]模型计算得到的启动时间较短，约为0.5 s. 这是因为文献[6]模型忽略了液压系统部分，假定火药爆炸产生的燃气作用力等于负载受到的驱动力，而实际上液压管路和液压阀都不可避免的存在压力损失，燃气作用力必然大于负载受到的驱动力. 因此，会导致系统提前启动. 同理，油缸运动到位时间也较本文仿真和试验结果提前约0.5 s左右. 本文仿真模型得到的位移曲线与试验曲线更为接近. 而由文献[6]模型计算得到的位移曲线在初始阶段波动更大. 这是因为，火药爆炸初期燃气腔内的压力变化迅速，且气体具有很大的压缩性，单纯考虑燃气的模型计算结果势必引起负载运动的波动，随着时间向前推移，逐渐稳定. 而考虑了液压系统的模型，由于液压油体积弹性模量非常大，且不可压缩，对整个系统而言，其本质是增大了系统的阻尼，系统响应则更为稳定.

如上所述，本文仿真计算得到的活塞杆位移结果与试验结果较为符合，其最大误差不超过15%. 经分析，误差是由于驱动过程中，装药燃烧效率、装置密封处存在泄漏、液压缸自身存在摩擦以及与外界存在热交换等因素造成的. 在后续研究中，需要对实验装置的导热性和密封性进行优化设计，并增加活塞摩擦、壁面传热、密封泄漏等过程的模型和装药参数的精确测试，以提供更为准确的试验与仿真结果.

总体上看，通过仿真与试验得到的结果基本一致，验证了起竖原理和联合仿真模型的有效性.

5 起竖系统仿真结果与分析

5.1 起竖性能分析

图5～图8给出导弹起竖过程中燃气挤压器辅助动力源的压力和流量变化曲线. 图9～图10给出导弹运动学参量的响应曲线.

图5是燃烧室和燃气腔压力随时间的变化曲线. 由图可知，燃气发生器点火启动后，装药开始燃烧，燃烧室内压力迅速上升，约0.2 s后即达到平衡压力21.2 MPa，建压完毕. 与此同时，燃气经喷管流入挤压式油箱的燃气腔，随着燃气的不断注入，燃气腔内气体压力同步上升，进而推动活塞运动，挤压油液腔内部的油液，使油液腔压力和液压缸无杆腔压力随之同步上升(如图7所示). 当无杆腔压力达到启动压力时，约0.3 s，导弹开始运动. 此后，随着导弹的加速运动，燃气腔容积迅速增大，导致燃气腔压力上升速度开始减缓，并于大约0.6 s左右达到峰值8.5 MPa，随后开始下降. 当在4 s关闭燃气挤压器时，装药同时燃烧完毕，燃烧室压力迅速下降至燃气腔压力.

图6是燃烧室喷管质量流量随时间的变化曲线. 由图可知，点火启动后，喷管流量迅速上升至稳定流量223.9 g/s. 对比图5中的燃烧室压力曲线发现，喷管质量流量和燃烧室压力正相关. 这是因为，燃气腔压力P2与燃烧室压力P1的比值P2/P1始终小于临界压力比0.553，由方程(8)可知，此时喷管质量流量不受燃气腔压力影响，在装药种类和燃气发生器结构参数确定的情况下，由燃烧室压力唯一确定，并且两者呈正比例关系. 此种工况下，喷管喉部始终处于超声速状态，而保证燃烧室喷管喉部始终处于超声速状态，是燃气驱动装置结构设计的前提条件，这也印证了燃气发生器设计的合理性. 在整个起竖过程中，燃气发生器是作为恒定流量源使用的.

图7是挤压式油箱油液腔和液压缸内压力随时间的变化曲线. 在启动初期，导弹保持静止状态，燃气挤压器输出流量为0(如图8所示)，油液腔和无杆腔处于联通状态，压力始终保持相等并同步上升. 在大约0.3 s时，导弹开始运动，燃气挤压器输出正流量，经电磁开关阀后产生压降，使得油液腔压力大于无杆腔压力.

图8是燃气挤压器输出流量随时间的变化曲线. 由图可知，系统启动后，燃气挤压器迅速输出大流量，并在1.1 s时达到瞬时最大流量，约2 038 L/min. 至3.2 s之前，基本保持在1 750 L/min左右，并最终在4 s内快速完成流量释放.

图9是导弹起竖角速度的时间响应曲线. 由图可知，点火启动后，导弹在燃气挤压器辅助动力源的作用下高速运动，起竖角速度快速上升，在1.1 s时达到峰值速度，约0.28 rad/s. 并且，在燃气挤压器作用的4 s内，平均速度达到0.18 rad/s. 4 s以后，燃气辅助动力源关闭，系统切换至液压泵主动力源继续起竖，平均角速度约0.027 rad/s左右. 对比可见，燃气辅助动力源起竖速度比液压主动力源起竖速度快6倍以上.

图10是导弹起竖角位移的时间响应曲线. 由图可知，导弹起竖臂在燃气挤压器辅助动力源作用的前4 s内即可达到0.72 rad(41°)左右，占全程起竖角度(90°)的46%，接近1/2. 由此可见，基于燃气挤压器式辅助动力源的起竖方案能够实现导弹的快速起竖.

5.2 起竖快速性和功率特性分析

为检验燃气挤压器式辅助动力源起竖系统的性能，将其与传统液压起竖系统进行仿真对比，两套起竖系统的液压参数均取相同的数值. 系统角位移θ和系统功率P随时间的变化曲线如图11和图12所示.

由图11可知，燃气辅助动力系统比传统液压起竖系统速度快，前4 s即可完成无辅助动力源系统29.5 s时的起竖角度，缩短起竖时间25.5 s，起竖快速性提高42.5%. 由图12可知，传统液压起竖系统装机功率为19 kW，满功率溢流；而基于燃气辅助动力源的起竖系统，辅助动力装置满足起竖初期大功率的需求，液压泵主动力源以低功率输出，起竖至一定角度后，负载压力减小，所需功率大幅下降，泵装机功率仅为11.6 kW，比传统液压起竖减少7.4 kW，装机功率降低38.9%.

同时注意到，燃气驱动向液压驱动切换过程中，角速度发生陡变，产生加速度，引起系统不稳定. 其原因可以结合图7系统的压力变化曲线说明如下：燃气驱动结束后，系统压力迅速下降，当切换至液压驱动后，又迅速抬升至负载压力，切换过程中液压缸无杆腔的压力波动会产生振动和冲击，从而引起负载运动不稳定. 在后续研究中，需要采取适当控制策略消除或减小压力波动，保证负载平稳运动.

两种动力源起竖系统主要性能参数对比如表2所示.

表2 两种动力源起竖系统主要性能参数对比

6 结 论

本文提出了一种基于燃气挤压器式辅助动力源的导弹快速起竖方案，建立了包含液压系统在内的起竖装置气、液、机多物理系统耦合数学模型，利用Matlab/Simulink和AMESim软件实现了起竖过程的联合仿真，搭建了系统的原理样机，分析了系统的起竖性能，对比研究了系统的快速性和功率特性，得出以下结论：

① 考虑液压系统的完整模型相比于不考虑液压系统的简化模型，系统在初期的动力学响应波动更小，运动更加稳定. 从起竖系统原理样机的试验结果可以看出，仿真结果与试验结果基本一致，验证了燃气挤压器起竖原理和仿真模型的有效性.

② 从起竖过程看，燃气发生器在毫秒量级内完成建压，喷管喉部始终处于超声速状态，符合燃气发生器结构设计的一般原则，印证了燃气发生器结构的合理性.

③ 新型液压动力源起竖系统可在34.5 s内完成起竖，装机功率仅为11.6 kW，较传统液压起竖系统在快速性上提高42.5%，在装机功率上降低38.9%，大幅提高了起竖装备的起竖速度，降低了系统的装机功率，能够为车载导弹武器发射系统的工程化设计与应用提供理论参考.

④ 燃气驱动向液压驱动切换过程中，角速度发生陡变，液压缸无杆腔压力产生波动，会对系统造成冲击，引起负载运动的不稳定. 在后续研究中，需要开展不同动力源之间平滑过渡切换控制问题的理论研究和试验工作，以确保负载平稳运动.