结合路径标签和数据变异的模糊测试关键数据定位方法

焦龙龙， 罗森林， 刘望桐， 潘丽敏

(北京理工大学 信息与电子学院，北京 100081)

模糊测试是威斯康星大学麦迪逊分校的Takanen等[1]在1988年提出的一种自动化漏洞挖掘方法[2]. 它首先生成大量畸形测试数据，然后监控被测程序处理这些畸形测试数据的过程，最后当被测程序发生异常时，就发现了一个潜在的安全漏洞[3]. 目前主要存在两种模糊测试方法：基于生成的模糊测试和基于变异的模糊测试[4].

基于生成的模糊测试需要利用输入规范来构建输入数据模型. 然而，在没有输入规范或者输入规范极端复杂的情况下，构建模型将是一件非常困难的事情[5]，使基于生成的模糊测试并不能够直接对输入规范未知的程序进行测试. 基于变异的模糊测试通过对原有的测试数据进行变异来生成新的测试数据，能够在没有输入规范的情况下完成测试工作. 由于很多程序并没有对输入进行严格的检测，这种方法同样是一种很有效的测试方法[6].

国内外的研究人员已经对格式未知的输入数据中的关键数据定位问题进行了比较多的研究，主要有人工定位、基于污点分析的定位方法和基于程序执行路径的定位方法.

人工定位是在分析输入数据格式信息的基础上，对其中包含的关键数据进行定位. 人工定位对分析人员的要求比较高，且一般需要比较长的时间. 另外人工定位依赖于格式逆向分析的结果，但是由于程序中使用的混淆、加密等方法，这类逆向分析的代价会变得非常大[7]. 以Samba项目为例，分析人员花费了12年的时间才成功完成SMB的逆向分析工作[8].

污点分析主要可以分为两类：粗粒度污点分析和细粒度污点分析. 粗粒度污点分析中，仅存在污染和未污染两个标签，最终的分析结果只能判断出某个位置是否被污染[9]，不能定位到污染的具体来源，比如陈厅[10]基于粗粒度污点分析实现的分析工具TVM. 细粒度污点分析为输入数据中每一个区域分配了不同的标签. 在分析结果中通过这些标签能够对污染来源进行定位，比如王铁磊[11]、梁晓兵[12]等实现的输入数据分析方法. 污点分析需要利用指令级的插桩来搜集数据，对程序的执行过程影响较大，搜集到的跟踪数据也比较庞大，整体的资源消耗较大. 另外，污点分析过程中，没有考虑程序对输入数据的验证过程，其定位结果存在比较多的误报.

Michal[13]提出一种利用程序执行路径信息对输入数据进行分析的方法. 该方法首先记录程序处理变异输入数据时的执行路径，然后通过分析执行路径的变化并结合输入数据本身的数字特征确定输入数据中各个部分的数据类型. 这种方法考虑了程序执行路径对分析结果的影响，但通过数字特征进行辅助定位的方式使结果中存在比较多的误报.

在使用变异的方式生成测试数据时，变异过程针对的是整个输入空间，而一个程序的输入空间通常是非常大的[14]. 但是，对于一个程序的输入数据而言，其中与安全敏感的危险操作(如内存分配、内存拷贝、字符串操作、含有格式化参数的函数等)相关的关键数据通常是非常少的. 这些关键数据控制着被测程序中的危险操作，对其进行变异具有更大的可能会触发程序中相关的漏洞，有助于提高模糊测试的效率[15]. 在缺乏输入规范的情况下，无法通过格式信息进行关键数据定位. 而现有的关键数据定位方法则存在资源消耗大、误报率高等问题.

针对这些问题，本文提出一种结合路径标签和数据变异的模糊测试关键数据定位方法，该方法通过插桩监控二进制程序处理输入的测试数据的过程，分析输入数据变异前后的处理过程的差异从而对输入数据中与安全敏感操作相关的关键数据进行定位.

1 关键数据定位方法

1.1 原理框架

针对模糊测试关键数据定位中存在的资源消耗大、误报率较高等问题，本文提出一种结合路径标签和数据变异的模糊测试关键数据定位方法，其原理如图1所示. 首先通过静态分析获取二进制程序及其依赖库中危险操作的位置；其次在动态分析的过程中使用动态插桩技术对危险操作进行监控并跟踪被测二进制程序处理输入数据的过程；然后结合输入数据的变异，得到程序处理这些数据的跟踪数据；最后通过分析跟踪数据获取关键数据的位置.

1.2 静态分析

通过静态分析能够对二进制程序中的危险操作进行定位，从而辅助输入数据中关键数据的定位工作. 静态分析包含两方面的工作：分析程序的依赖库；对程序及其依赖库中的危险操作进行定位.

一个程序在执行时通常需要多个动态库的辅助，即程序的依赖库. 这些库中同样会包含一些危险操作. 依赖库的分析可以使用程序文件对应的可执行文件分析工具完成，比如Linux下使用ldd命令即可查看ELF格式的可执行文件的依赖库.

程序中内存分配、内存拷贝、字符串操作、含有格式化参数的函数等容易引起安全问题，对这些代码进行测试有更大的可能发现问题[12]. 因此将这些函数定义为危险操作，主要危险函数如表1所示. 程序执行过程所需的函数信息会记录在程序文件的某个区域(如符号表、导入表)，利用程序逆向分析技术即可通过文件格式信息对这些函数进行定位.

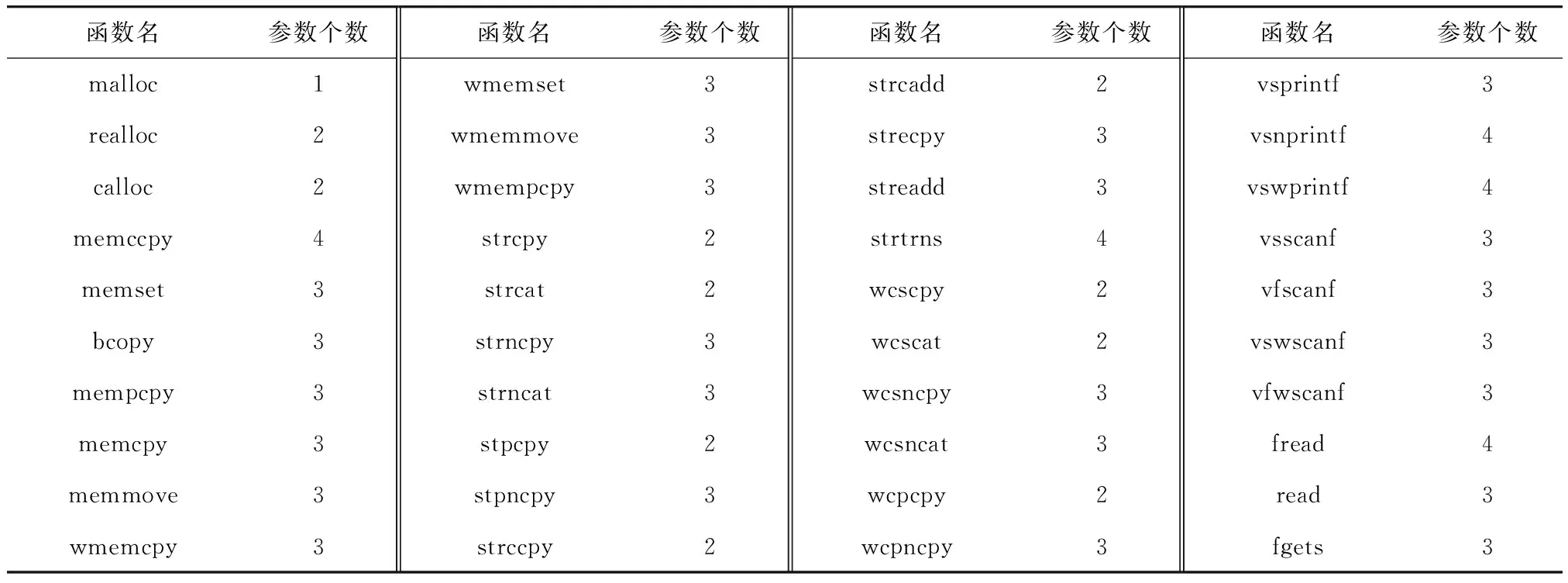
表1 包含危险操作的函数

1.3 动态分析

动态分析部分完成实际的关键数据定位工作，具体过程如下：首先，利用插桩技术跟踪监控被测程序的执行过程以及其中包含的危险操作；其次，记录被测程序对初始输入数据的处理过程以及其中包含的危险操作；然后逐个变异初始输入数据中的每个字节，记录被测程序处理这些变异数据的过程以及其中包含的危险操作；最后通过对比分析输入数据变异前后记录到的程序跟踪数据来进行关键数据定位.

1.3.1数据变异

使用变异操作能够以初始输入数据为模板，生成大量新的输入数据. 变异的过程无需输入数据的规范，适用于各种格式的数据. 假设初始输入数据为X，共包含n字节，当对X中的第k字节使用变异操作m后将得到新的输入数据Xm,k，这样的一次变异过程可以使用一个函数来表示，即Xm,k=m(X,k)(1≤k≤n).

本文方法在关键数据定位过程中主要通过数据变异的方式观察二进制程序执行过程的变化. 定位过程中并不会尝试使用变异的方式遍历整个输入空间，仅利用位翻转的方式依次对X中每一个字节进行轻微变异，将这个变异操作记为mb，那么针对第k字节的变异将得到新的输入数据Xmb,k. 该变异过程同样可以使用一个函数来表示，即Xmb,k=mb(X,k)(1≤k≤n).

1.3.2程序跟踪

程序跟踪主要是监控并记录被测程序的执行过程. 程序执行过程中需要依赖库的支持，因此程序跟踪需要能够同时对程序及其依赖库中的代码执行过程进行监控. 每一个程序及其依赖库都是同一种格式的可执行文件. 使用E表示一个可执行文件，同时假设程序及其依赖库共有w个可执行文件，那么可将这些可执行文件视为集合P={E1,E2,…,Ew}. 可执行文件E的代码可以被划分成很多基本块. 使用B表示一个基本块，同时假设可执行文件Ei的代码可划分为Li个基本块，那么可将Ei视为基本块的集合EBi={Bi,1,Bi,2,…,Bi,Li}.

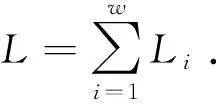
PB=∪EBi={B1,B2,…,BL}.

(1)

程序执行的过程就是按照某种顺序执行集合PB中的基本块，因此执行过程的监控可以转换为监控正在执行的基本块，执行过程的记录则可以转换为记录执行过的基本块序列.

一个基本块B有且只有一个入口和一个出口，在其执行过程中仅会从入口处开始执行并从出口处结束，故使用基本块的入口地址b能够代表一个基本块并且具有唯一性. 利用基本块插桩能够在基本块B的入口处获取到基本块的入口地址b. 因此，基本块的集合PB可以使用基本块的入口地址的集合Pb表示，即PB≡Pb={b1,b2,…,bL}.

使用S代表程序的执行过程，那么当程序执行过j个基本块时，其执行过程可记为一个由j个基本块入口地址组成的序列Sj=(b1,b2,…,bj)，其中∀1≤i≤j∶bi∈Pb.

程序在执行时可能包含多个线程，每个线程均有自己的执行过程，需要分别记录每个线程的基本块序列，使用线程ID区分不同线程的基本块序列，即将线程x的基本块序列记为Sx,j. 综上所述，程序跟踪将得到一个或多个基本块序列，每个基本块序列对应程序中一个线程的执行过程.

1.3.3危险操作监控

对危险操作的监控需要记录危险操作对应的函数的名称、路径标签和参数. 通过静态分析能够得到函数的位置，进而利用动态插桩技术在函数的起始位置处进行插桩，就可以在函数实际执行前记录函数的相关信息.

将某个危险操作D对应的函数名称记为fn. 在动态插桩时，可以从静态分析的结果得到fn的相关信息. 因此可将名称fn的记录工作写入插桩的代码中，在执行到危险操作D时直接进行fn的记录.

假设危险操作D所在的线程x在执行到D时共执行过j个基本块，那么危险操作D对应的执行路径就是Sx,j. 执行路径Sx,j本质上是一个地址序列，可以当作一个基本块入口地址组成的数组来处理，将这个数组通过哈希运算得到哈希值h作为路径标签t. 那么执行到危险操作D时的程序执行路径可使用路径标签t表示.

将哈希运算视为一个函数H(salt,data)，其中salt为计算哈希值时使用的初始值，data为需要计算哈希值的数据. 哈希运算H将一个基本块地址b作为哈希计算的基本单位，设哈希运算H中对一个基本块地址b进行哈希计算的过程为函数HH(salt,b).

当data中只有一个基本块地址b时，直接使用HH进行哈希计算，即h=H(salt,b)=HH(salt,b). 当data中含有多个基本块地址时，设data=Sx,j=(b1,b2,…,bj)，采取依次对每一个基本块进行哈希的方式进行计算，并且将前一个地址得到的哈希值作为下一个地址进行哈希计算时的salt，整个过程如式(2)所示.

(2)

使用上述计算过程，意味着路径Sx,j的哈希值hj可以在执行到基本块bj时，通过前一个路径状态Sx,j-1的哈希值hj-1经过一次简单的哈希计算得出，无需从b1开始进行计算，能够减少许多不必要的计算. 综上，可将Sx,j的哈希值hj作为危险操作D的路径标签t.

函数参数的记录需根据运行环境进行区分. 不同的运行环境下，每个函数的参数有不同的储存方式，通过函数的调用约定可以获取其参数的储存位置. 例如x86平台下主要有cdecl、stdcall和fastcall 3种函数调用约定，所有调用约定中，函数参数均储存在寄存器或线程栈中. 因此，在函数执行前根据调用约定和函数定义读取寄存器和线程栈中的数据即可获取函数参数. 当函数有g个参数时，函数参数可按照从左到右的顺序记为一个参数序列PA=(p1,p2,…,pg). 定义函数gp()为从参数序列PA中获取第k个参数，那么pk=gp(PA,k)(1≤k≤g).

综上所述，对于一个危险操作D，通过危险操作监控将得到D的函数名fn、路径标签t、参数序列PA. 使用一个三元组(fn,t,PA)表示危险操作D的相关信息并将其记为I，即I=(fn,t,PA). 同时分别使用I[0]、I[1]、I[2]代表三元组I中的数据fn、t、PA.

将程序跟踪和危险操作监控的过程抽象为一个函数Trace()，那么一个输入数据X在经过函数Trace()的处理后，将得到一组关于危险操作的跟踪数据，使用集合T表示这组跟踪数据，整个过程如式(3)所示为

T=Trace(P,X)={I1,I2,I3,…}.

(3)

1.3.4跟踪数据分析

设初始输入数据X对应的跟踪数据集合为T0=Trace(P,X)，变异输入数据Xmb,k对应的跟踪数据集合为Tk=Trace(P,Xmb,k)(1≤k≤n).

危险操作D对应的函数为fn，如果函数fn的某个参数来源于输入数据，那么输入数据就能够对这个参数进行一定程度的控制. 输入数据中能够控制危险函数参数的数据就是所要查找的关键数据. 也就是说，如果存在Ia∈T0、Ib∈Tk、c使Ia[0]=Ib[0]、Ia[1]=Ib[1]以及gp(Ia[2],c)≠gp(Ib[2],c)均成立，那么第k字节变异后的输入数据造成了同样位置的相同危险函数的参数发生变化，即第k字节能够控制危险操作的参数，因此将第k字节标记为关键数据. 通过这种方式逐个分析输入数据X中的每一个字节，能够获取到所有符合要求的字节，并得到关键数据的集合SK.

跟踪数据分析的过程可以使用算法1来表示，其中函数GetElement(T,t)(第2行)是从跟踪数据集合T中取出路径标签是t的跟踪数据. 如果以路径标签为键(Key)将跟踪数据集合T0转换为一个哈希表，那么可以将从集合中取数据的操作优化为常数时间，因此每一轮的分析工作耗时将仅与Tk的大小相关. 另外，从算法中可以看出，在定位过程中，需要长期储存的仅有初始输入数据X的跟踪数据集合T0.

算法1跟踪数据分析

输入T0：初始输入数据X的跟踪数据集合

Tk：变异输入数据Xmb,k的跟踪数据集合

SK：关键数据位置集合

输出SK：更新后的关键数据位置集合

1.foreachIainTkdo

2.Ib=GetElement(T0,Ia[1])

3.ifIb!= null do

4.ifIa[0]==Ib[0] do

5.g=Ia[2]中元素的个数

6.forc= 1 →gdo

7.ifgp(Ia[2],c)！=gp(Ib[2],c) do

8.SK=SK∪k

9.returnSK

10.endif

11.endfor

12.endif

13.endif

14.endfor

15.returnSK

2 实验分析

2.1 实验目的和数据源

使用本实验测试本文提出的方法进行关键数据定位时的准确性，并与模糊测试工具AFL[13]中的AFL-Analyze模块进行对比. 使用4个常见的文件处理型程序作为实验中的被测程序：图片格式转换程序ImageMagick convert(IMC)7.0.5-6[16]和XnSoft NCONVERT(XSN)v6.88[17]；ZIP文件解压缩程序UnZip 6.00[18]；ELF文件分析程序GNU readelf 2.24[19].

2.2 实验环境和条件

本实验主要在一个VMware上搭建的Ubuntu 14.04虚拟机中进行，为其分配4核2.50 GHz的CPU和4 GB内存. 数据格式分析部分在Windows 7下使用010 Editor进行.

2.3 评价方法

测试中使用的输入数据均是格式已知的数据文件，可以通过格式分析获取其中每个字节代表的意义. 与危险操作相关的敏感数据主要包括长度值、宽度值、数量值、大小等类型的数据，这些敏感数据中的部分数据在变异后将无法通过程序的验证或者不能改变程序的执行过程和结果，去除这些数据的影响，将剩下的敏感数据标记为关键数据.

使用关键数据定位的精确率P、查全率R、误报率F作为评价标准，其计算方法如式(4)～(6)所示.

P=PT/(PT+PF)×100%.

(4)

R=PT/(PT+NF)×100%.

(5)

F=PF/(PF+NT)×100%.

(6)

式中:PT为将输入数据中的关键数据正确判定为关键数据的个数;NT为将输入数据中的非关键数据判定为非关键数据的个数;PF为将输入数据中的非关键数据判定为关键数据的个数;NF为将输入数据中的关键数据判定为非关键数据的个数.

2.4 实验过程和参数

① 准备输入数据. 为IMC和XSN准备9个不同格式的图片文件(BMP、DDS、GIF、ICO、JPEG、PCX、PNG、TGA、TIFF)，为UnZip准备ZIP格式的文件，为readelf准备ELF格式的文件. 使用010 Editor中分析这些作为输入数据的文件，记录文件大小、文件中的敏感数据. 使用各个被测程序处理这些文件，统计处理过程中程序执行过的指令数.

② 分析输入数据. 依次变异步骤1中记录的敏感数据(每次仅变异一个字节)，使用相应的被测程序处理变异后的数据. 查看处理结果，记录其中变异后无法通过程序验证或者不能改变执行过程和结果的数据. 其中，对于readelf，将变异后仅能造成程序显示的结果中的数字发生变化的字节也标记为不能改变程序执行过程的项.

③ 使用本文的方法分别对各个被测程序进行测试，记录被标记的字节、跟踪文件的大小、每次分析的耗时. 将标记的字节与步骤1、2中的分析结果进行对比并记录结果.

④ 使用AFL-Analyze分别对各个被测程序进行测试，记录标记为长度类型的字节、每次分析的耗时. 将标记的字节与步骤1、2中的分析结果进行对比并记录结果.

2.5 实验结果

初始输入数据的分析结果如表2所示. 按不同的文件格式考虑，输入数据中包含的敏感数据共440字节，占输入数据的3.83%. 考虑不同被测程序对输入的处理，则敏感数据有704字节，所有的敏感数据中有246字节在变异后无法通过被测程序的验证，335字节在变异后无法造成变化，两种数据共581字节，即输入数据中共包含关键数据123字节.

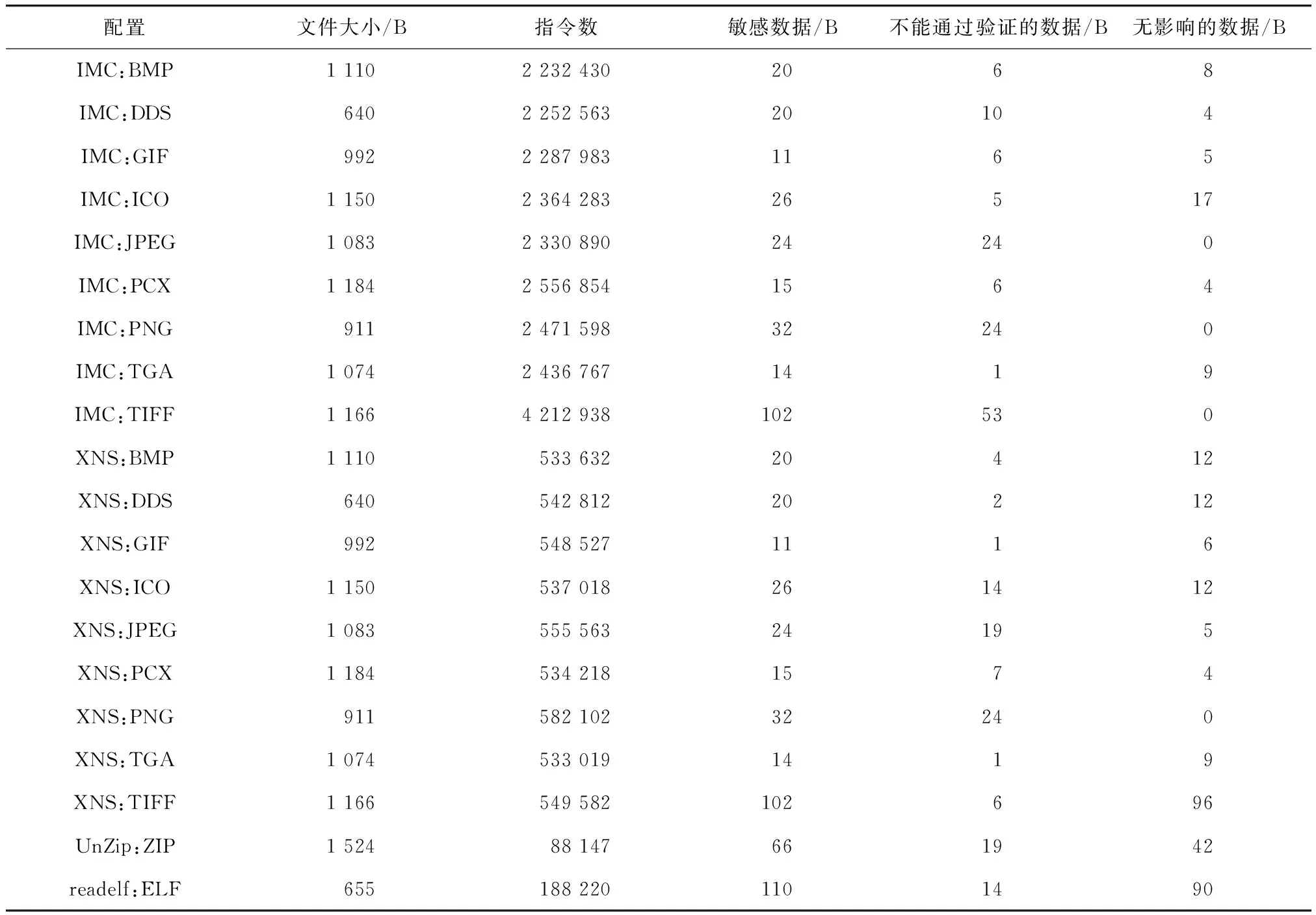
表2 初始输入数据分析结果

关键数据的定位结果如表3所示. 本文的方法的分析耗时在分钟级，跟踪文件的大小在kB级，共将146字节标记为关键数据，其中确实是敏感数据的有137字节，是关键数据的有91字节. 本文方法的关键数据定位精确率为62.33%，查全率为73.98%，误报率为0.266%. AFL-Analyze的分析耗时在分钟级，共将410字节标记为关键数据，其中确实是敏感数据的有157字节，是关键数据的有17字节. AFL-Analyze的关键数据定位精确率为4.15%，查全率为13.8%，误报率为1.90%.

表3 关键数据定位结果

3 讨 论

实验中使用的输入数据共包含关键数据123字节，在所有数据中占比仅为0.6%. 本文方法对91字节的关键数据进行准确定位，是AFL-Analyze的5.35倍；本文方法的定位精确率为62.3%，是AFL-Analyze的15.02倍；AFL-Analyze将393字节的数据误报为关键数据，是本文方法的7.15倍. 本文方法有32字节的关键数据未能定位到，对这32字节的数据进行分析发现，这些字节变异后，被测程序在处理变异后的输入数据时，程序执行过程会发生部分改变，导致危险操作的路径标签发生改变，进而影响本文方法的定位过程.

如果将误报率的计算范围缩小到敏感数据，那么本文方法的误报率为7.92%，AFL-Analyze的误报率为24.1%. 如果将定位结果的判定标准扩大到敏感数据，那么本文方法的精确率为93.8%，查全率为19.5%，误报率为0.045%；AFL-Analyze的精确率为38.29%，查全率为22.3%，误报率为4.15%. 本文方法的精确率和误报率优于AFL-Analyze，但在查全率上低于AFL-Analyze. 这两种情况说明AFL-Analyze更倾向于将可疑数据标记为敏感的关键数据，使其能够发现更多的敏感数据，同时也会造成较多的误判导致精确率下降. 而本文方法通过路径标签和数据变异排除程序中数据验证过程的影响，降低了误报率. 对两种方法误判的字节进行分析发现，本文方法误判的字节虽然并不是关键数据，但其在变异后会导致被测程序在处理数据时出现偏差，影响到部分危险操作的参数；AFL-Analyze误判的字节中很多为类型标志，变异后将导致输入数据无法通过验证.

AFL-Analyze的分析过程不需要额外的数据存储，而本文方法需要储存跟踪数据，并且被测程序处理输入时使用的指令数越多，跟踪数据越大，相应的分析耗时也会越长. 其中，本文方法在以UnZip为被测程序的定位实验中，总的耗时明显与其指令数不相符. 这主要是因为本文方法在跟踪被测程序时利用了fork机制对整个分析过程进行加速，而UnZip并不能够很好地与这种加速方法兼容，导致运行速度相对较慢进而影响了整体的分析耗时. 另外，在针对DDS格式的输入数据进行的定位实验中，本文方法和AFL-Analyze的分析耗时均明显小于其他图片格式. 这主要是因为本文方法和AFL-Analyze在分析过程中均需要对输入数据的每一个字节都进行变异，整个分析过程的耗时会随着输入数据长度的增加而提高. 实验中使用的DDS格式的输入数据的长度约为其他图片数据的60%，因此DDS格式的输入数据的分析耗时会更少.

与细粒度污点分析方法相比，本文方法在跟踪被测程序时记录的数据量更少. 通过模拟一般细粒度污点分析记录跟踪数据的过程，得到细粒度污点分析的跟踪数据的大小，如表4和表5所示. 本文方法记录的kB级跟踪数据远小于一般细粒度污点分析的MB级跟踪文件. 另外，细粒度污点分析方法没有对得到的结果做过多的分析，不能区分变异后无法通过验证的数据，会存在比较多的误报.

表4 细粒度污点分析跟踪文件的大小(1)

表5 细粒度污点分析跟踪文件的大小(2)

4 结 论

提出了一种结合路径标签和数据变异的模糊测试关键数据定位方法，该方法首先通过静态逆向分析对二进制程序中的危险操作进行定位；然后利用基本块插桩记录程序的执行路径，同时利用函数插桩获取程序执行过程中危险操作的参数，并将执行到某个危险操作时程序执行过的基本块序列的哈希作为该危险操作的路径标签；最后通过分析输入数据变异前后相同路径标签下同一个危险操作的参数变化来进行关键数据定位. 实验结果表明，本文方法能够以较低的资源消耗对输入数据中的关键数据进行定位，整体的精确率为62.33%，查全率为73.98%，误报率为0.266%. 本文方法仍然存在一些无法发现的关键数据，为了解决这一问题，下一步将研究如何利用细粒度污点分析的思想提高关键数据定位的查全率.