钢管结构相贯节点研究综述

周小燕

（甘肃省建筑设计研究院有限公司，甘肃 兰州 730030）

1 概述

钢管相贯节点最初应用与平面及立体管桁架结构中，近年来由于其外观的优越性，在许多的复杂大跨度空间钢结构中被越来越广泛的应用，但是由于结构体系的复杂性，钢管相贯节点的设计也越来越复杂，往往是很多个杆件交汇于一个节点处。常用的钢管主要是圆钢管和方钢管，在相贯节点中按照腹杆的位置不同，可以分为间隙相贯节点和搭接相贯节点。常用的平面相贯节点类型有T型、X型、K型，空间相贯节点则是在平面相贯节点的基础上衍生出来的。在实际很多的空间结构中，往往是很多个杆件交汇，节点受力状态非常复杂，已经超出了规范中的典型相贯节点的分类，整个结构在外力作用下的受力性能更依赖于节点的稳定而非构件本身的强度，节点破坏往往先于构件发生。

1.1 国内研究现状

刘鑫刚和葛家琪[1]等结合贵阳奥体中心体育场，对承受弯矩的大直径钢管相贯节点进行了足尺模型极限承载力破坏试验。通过模型试验来研究承受弯矩大直径相贯节点的设计承载力，并考虑偏心对相贯节点承载力的影响，指出节点腹杆的偏心会降低节点承载力，建议采用设置加劲板的方式提高节点承载力。陈以一[2]等以整体钢管桁架为试验加载对象，对两种圆钢管空间相贯节点进行静力和反复加载试验研究，研究了杆件的承载力与节点承载力的关系及节点的几何特性与耗能能力的关系。武振宇[3]等对Y形矩形钢管节点进行拟静力试验，分析研究了节点的延性比、承载力和能量耗散系数等参数。李自林[4]等对4组N形圆钢管相贯节点进行了滞回试验研究，采位移延性系数评价了节点的延性性能及耗能能力，分析了垫板加强和弦杆内填混凝土两种加强措施对节点的延性和承载力的影响，发现弦杆内填混凝土可以有效提高节点的承载力，但会降低节点的延性；采用加强垫板的相贯节点则可以提高延性，承载力提高的幅度有限。郑伯兴和黄长华[5]等总结了目前钢管相贯节点研究中存在的几个较为常见的疑难问题：钢管节点刚度假定、极限承载力的确定、有限元单元类型的选取、有限元模型约束的模拟和考虑弦杆荷载的规范公式的使用。通过分析,总结了这几个常见疑难问题的解决对策。杨维国和王耀峰[6]等人应用有限元软件ANSYS对XKK型空间相贯节点进行分析，研究了相贯节点中主支管管径比、腹杆与主管管径比、主管与腹杆的夹角及间隙及径厚比等参数对节点承载力的影响，此外研究发现XKK型空间相贯节点在进入弹塑性阶段后有较长的塑性区段，XKK型空间相贯节点有较好的延性能力。李斌[7]总结了管桁架节点的失效模式及识别方法，并结合具体实例对节点的失效模式进行有限元分析，并提出在加工及施工过程中相应的构造处理措施。朱邵宁和舒兴平[8]运用有限元软件ANSYS对某体育场崖盖结构中两个空间KK型圆钢管相贯节点进行分析，总结了节点在荷载作用下的力学性能，并提出在满足承载力的情况下，可对杆件的壁厚进行适当的经济性优化。祝磊[9]结合实际工程对空间矩形相贯TX型节点进行了有限元分析，并考虑了平面外弯矩的影响，研究表明不同的荷载路径对节点承载力的影响是可以忽略的，利用线性回归软件ORIGIN回归出TX型节点承载力计算的拟合公式。熊俊和石永久[10]等以北京市某空间网壳结构植物园的焊接管节点为例，采用有限元软件ABAQUS分析了节点在各种内力组合作用下的应力、应变分布，计算了节点承载力的安全系数，分析了节点的三种破坏形态，分析探讨了设置加劲肋对节点承载力的影响。郑江、郝际平[11]等以某体育馆相贯节点为例，选用合理有效的多尺度计算模型，用有限元软件ANSYS对其在弹性及弹塑性阶段的力学性能进行了分析，并提出来判别复杂空间相贯节点承载力的准则。E.M.Dexter[12]对轴向荷载作用下的搭接和小间隙K形相贯节点做了大量有限元分析，并将计算的结果与现有设计指南中的结果进行了比较。研究表明，节点的重叠部分的支撑作用可以提交节点的承载力。Scolar[13]等通过对7个V型相贯节点和5个T型相贯节点进行了轴向载荷试验，被测试件的支弦直径比为0.22～0.65，弦径比为13～23。V型节点的分支之间的夹角为60°、90°或120°。试验对比了T型和V型相贯节点试件的极限强度、刚度和应力等力学性能。在T型接头处增加平面外支杆，当支杆之间的夹角较小时增加T型节点的强度，在夹角较大时减小T型节点的强度。

1.2 圆管相贯节点有限元分析

节点建模：选取一空间结构中典型圆钢管相贯节点，采用通用有限元软件ABAQUS进行计算分析，在前处理中，利用Rhinoceros软件强大的建模技术，采用体元将钢管建成空心钢管圆柱体，按照杆件之间的相贯顺序进行体元之间的相减运算，得到各腹杆的相贯边缘线，删除多余的相交处的体元，对所有交汇杆件进行布尔运算，得到钢管相贯节点模型。

单元类型：节点采用实体单元C3D10。

材料：理想弹塑性材料，弦杆及腹杆均采用Q345，fy=310MPa，E=2.06×105MPa。 泊松比取 0.3。节点区的选取及网格划分：对于钢管相贯节点，计算模型的合理选取很重要，杆件长度太长将导致弦杆过早发生弯曲破坏，而长度过短又会使弦杆出现明显的凹凸变形，文中弦杆长度取由节点中心开始外伸约4倍的杆件直径，腹杆均由两相交杆件的根部开始外伸取腹杆长度的1/4，有利于消除端部加载方式对节点区域的影响。网格划分采用ABAQUS中自由网格划分，且对相贯线附近易产生应力集中的区域进行人工干预来细分网格以得到较好的计算结果。（如图1所示）。

图1 节点有限元模型

边界条件及加载方式：对主弦杆一端按固定端考虑，另一端只允许杆件轴向发生位移，腹杆主要承受轴力作用。杆件截面见表1。

表1 杆件截面及荷载组合

判别准则：以文献11中提出的极限变形作为节点极限承载力的判别准则，采用0.008d作为变形限值（d为弦杆直径）。

第一阶段选取整体计算模型中弦杆1和弦杆2轴力最大时的两种荷载工况进行弹性分析 （见表1）。分别选取弦杆1和弦杆2在杆件轴力达到最大时的荷载工况进行内力分析。图2为工况组合一作用下节点的Mises等效应力分布，图中可以看出，在设计荷载作用下，节点处于弹性阶段，核心区处最大应力为152N/mm2。第二步采用逐级加载的方式进行弹塑性分析，对各支管的轴力以一定的比例进行加载，图3为加载至设计内力的2.5倍时的内力云图，在节点核心区的最大应力为397N/mm2，钢材进入塑性区域贯通弦杆2，此时的变形值为2.78mm，基本接近极限变形值2.81mm。

图2 组合一作用下的Mises弹性应力分布图

图3 组合一作用下的Mises塑性应力分布图

图4为工况组合二作用下节点的Mises等效应力分布，节点基本处于弹性阶段，核心区处最大应力为320.6N/mm2。第二步进行弹塑性分析，图5为加载至设计内力的2倍时的内力云图，在节点核心区的最大应力为520N/mm2，钢材进入塑性区域贯通弦杆2，节点相连杆件基本已经进入屈服，此时的变形值为2.98mm。

图4 组合二作用下的Mises弹性应力分布图

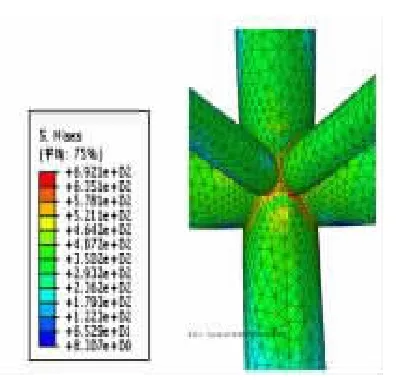
图5 组合二作用下的Mises塑性应力分布图

上述钢管相贯节点有限元分析结果表明，在正常设计荷载作用下，支管与主管相交区域的应力较大，局部出现应力集中现象，远离相贯线处的应力越来越小，节点整体的应力分布较为平缓，且节点区域没有出现较大的变形，应力均小于钢材的屈服应力，当继续对上述节点加载至正常荷载的2～2.5倍时，节点相贯线处应力明显增大，但仅仅是在节点相贯线处的局部区域出现的明显屈服现象，但整个节点的位移还是比较小的。通过分析表明，上述节点的设计是安全可靠的。

2 结论与展望

目前，国内对相贯节点的研究还比较少，尤其在复杂空间结构中相贯节点的复杂多样性，规范中仅对一些典型节点的承载力做了规定，对于相贯节点的节点加强做法的研究更是比较少。文章对国内相贯节点的研究现状总了综述性的论述，并选取了一典型的圆钢管相贯节点进行了有限元分析，分析结果表明在正常荷载作用下相贯节点的节点满足设计要求。