基于经度变换法的单台链双曲线定位GDOP计算
王璐璐,何在民,韩振兴,黄媛媛,鲁刚
基于经度变换法的单台链双曲线定位GDOP计算
王璐璐1,2,3,何在民1,2,韩振兴4,黄媛媛1,2,3,鲁刚1,2,3
(1. 中国科学院 国家授时中心,西安 710600;2. 中国科学院 时间频率基准重点实验室,西安 710600;3. 中国科学院大学,北京 100049;4. 中国人民解放军63768部队,西安 710600)
无线电双曲线定位精度与几何精度衰减因子(GDOP)密切相关。针对单台链双曲线定位GDOP值计算存在区域划分判定不明确的问题,提出的经度变换法使得GDOP值计算更加准确、有效。以阿尔法无线电导航系统为例,计算并分析其在(20°N,30°E),(80°N,150°E)所围大矩形区域的GDOP值,结果表明:所提方法可实现Ⅰ、Ⅲ与Ⅱ、Ⅳ区域的有效识别,在Ⅱ、Ⅳ区域内,GDOP值计算准确度平均提升了13.07%,在(29°N,103°E),(37°N,114°E)所围矩形区域内,GDOP均小于5,保证了试验验证的可用性。
经度变换法;几何精度衰减因子(GDOP);区域识别;单台链;双曲线定位
0 引言
陆基无线电定位可采用圆圆伪距定位和双曲线时差定位两种方式,这两种定位方式的定位误差主要取决于两个因素[1-3]:①圆圆定位的伪距测量误差和双曲线定位的时差测量误差;②发射台分布的GDOP(geometrical dilution of precision)。其中伪距测量误差和时差测量误差取决于系统发播、无线信号传播以及接收终端等引入的各种误差,而GDOP则取决于发射台分布的几何关系[4-5]。因此,GDOP计算对于分析陆基无线电导航系统定位精度至关重要[6-8]。
文献[9]提出了单台链双曲线定位GDOP计算模型,并基于提出模型推导出GDOP计算解析表达式,其GDOP值由台间相关系数、对台张角以及双曲线交点夹角共同决定;文献[10]利用文献[9]给出的解析表达式,在取台间相关系数等于1的条件下,以GDOP值为参考分析了俄罗斯阿尔法导航系统的定位精度,但未考虑双曲线交点夹角分区域取值不同的问题;文献[11]分析了罗兰C单台链双曲线位置线的GDOP的计算过程,同时考虑了分区域求双曲线交点夹角,但未给出区域划分的计算方法。针对单台链双曲线定位GDOP计算存在的不足,笔者提出区域识别的经度变换法,解决单台链GDOP计算区域识别问题,更加客观地实现了单台链双曲线定位GDOP计算。以俄罗斯阿尔法系统为例,选取(20°N,30°E),(80°N,150°E)所围大矩形区域,在完成经度变换法区域识别的基础上进行GDOP计算,同时选取(29°N,103°E),(37°N,114°E)所围矩形区域进行仿真验证,给出GDOP计算结果及其等值线曲线。
1 基于区域识别的GDOP计算方法
单台链双曲线定位GDOP计算公式[9]如下:
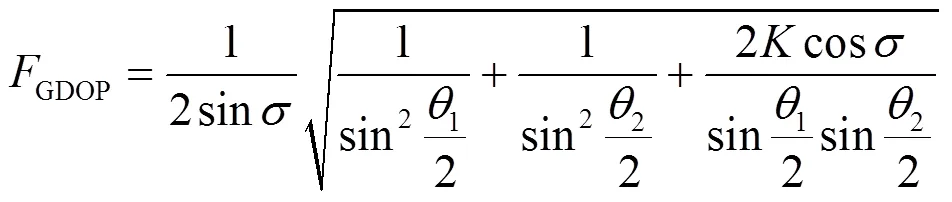
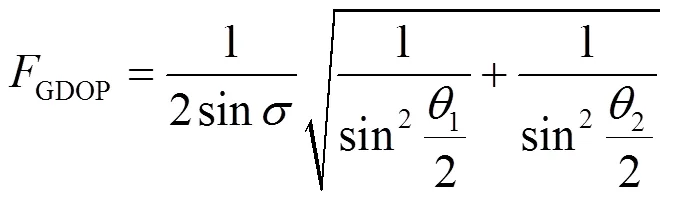

图1 单台链双曲线定位区域划分图


当位于Ⅱ、Ⅳ区域时,
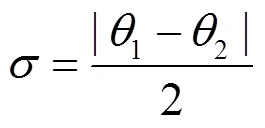
1.1 归化纬度转换
图2描述了大地纬度、地心纬度和归化纬度之间的转换关系[12]。图2中,为椭圆短半轴,为椭圆长半轴,为椭球离心率,作以原点为中心、半径为的辅助圆。
图2 大地纬度、地心纬度和归化纬度的定义
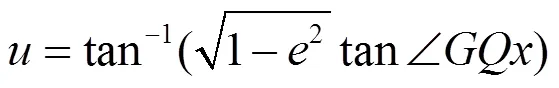


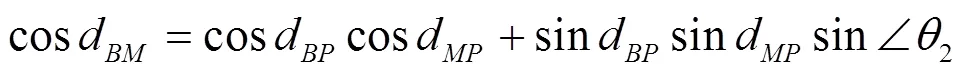
1.3 经度变换法的区域识别
经度变换法判断点位置的核心就是经过两次叉乘运算建立以主台为北极,点为零度经线的新坐标系,同时构建正交矩阵,原坐标系中的坐标通过正交矩阵映射到新坐标系中,并在新坐标系下计算台链所有台站与定位点的经度,从而实现区域识别,具体步骤如下:
① 球坐标到直角坐标转换
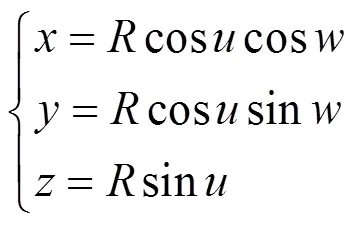
② 新坐标系确定
图3 新坐标系确立示意图
③ 新坐标系下表示

④ 经度计算与象限判断
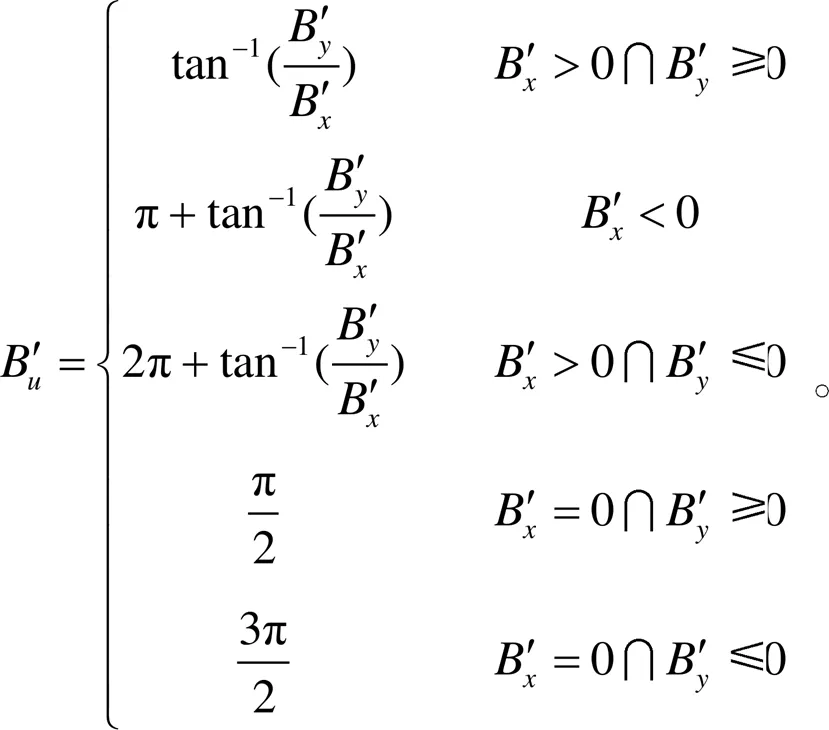
2 GDOP计算结果与分析
陆基远程无线电导航资源主要包括罗兰C(长波)无线电导航系统和阿尔法(甚长波)无线电导航系统[13-14],其中阿尔法无线电导航系统是现在唯一还在使用的甚低频无线电导航系统,工作区可覆盖全球70%的面积,系统所属5个台站信息如表1所示,其中的主台、东副台和西副台3个发射台发播信号,是我国可利用的导航资源。本文以俄罗斯阿尔法无线电导航系统为研究对象,计算并分析其在给定区域的GDOP值。

表1 阿尔法无线电导航系统台站信息
为了分析所提方法正确性,选取的区域范围要足够大,区域内得涵盖Ⅰ、Ⅲ与Ⅱ、Ⅳ 4个区域。本文以阿尔法导航系统主台、东副台和西副台3个台站为导航台,定位点位于(20°N,30°E),(80°N,150°E)所限定的大矩形区域内。依据经度变换的GDOP计算方法,得到GDOP计算流程如图4所示。
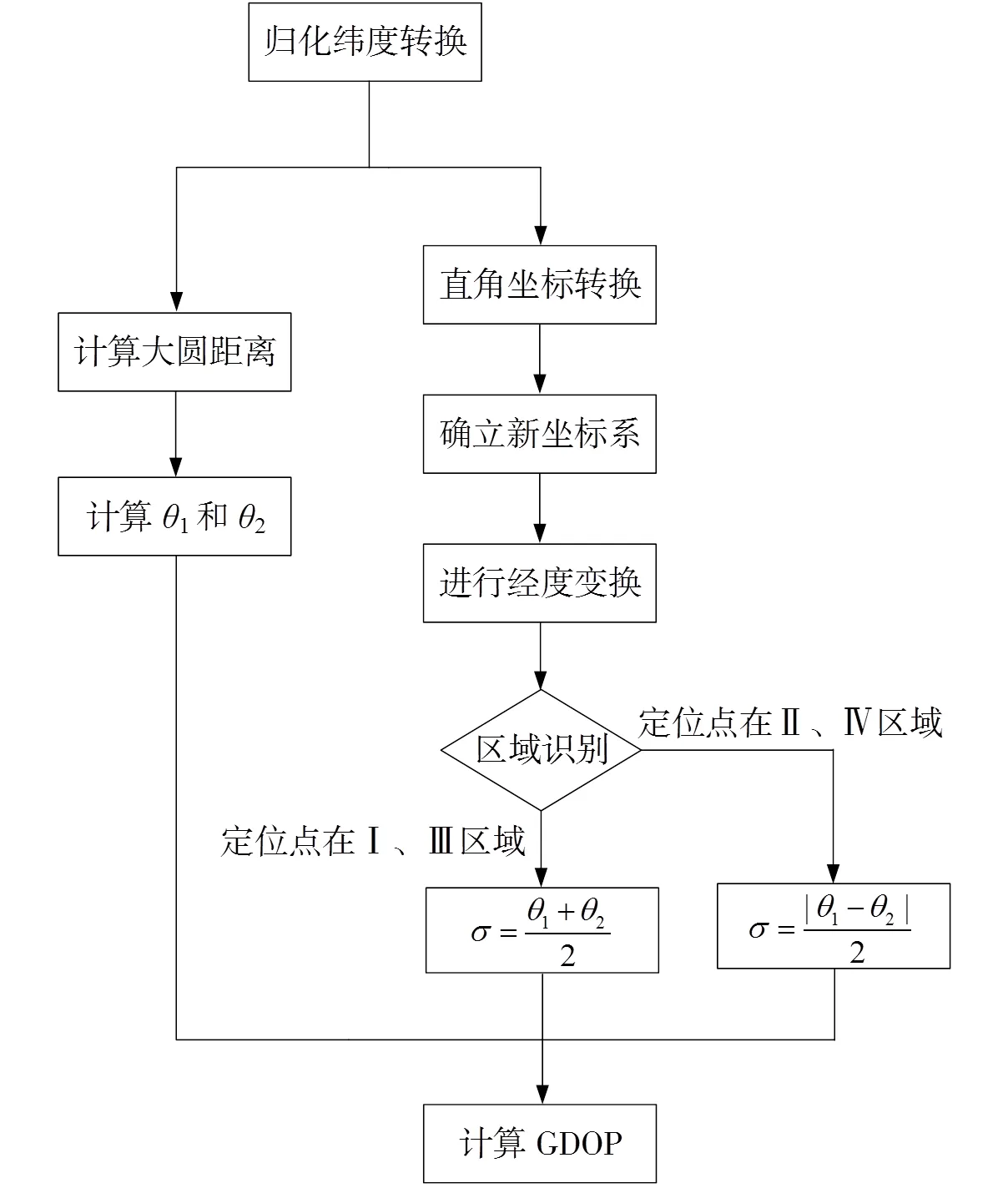
图4 GDOP计算流程
在计算过程中,定位点在所选大矩形区域内,以经纬度1°为步进量,划分区域网格,遍历区域网格中的7 381个点网格点,每个网格点均采用经度变换法进行区域识别并进行GDOP计算。


图5 台站与大矩形区域相对位置示意图

图6 经度变化法在大矩形区域的区域识别结果
由于后期要进行试验验证,为提升试验验证数据的代表性、有效性及可用性,现选取(29°N,103°E),(37°N,114°E)矩形区域。所选区域覆盖山地、丘陵、森林、平原、高原、平川、河谷、沙漠及戈壁等地貌,地形地貌多样、复杂,有利于后期试验中验证阿尔法无线电导航系统在不同地貌地区的定位精度,其结果如表2所示,同时绘制了GDOP值分布等值线,计算结果见图7。

表2 阿尔法无线电导航系统在试验区域的GDOP值分布表

图7 阿尔法无线电导航系统在试验区域的GDOP等值线
根据表2和图7,能直观形象地得到GDOP值的分布情况与变化趋势:定位点经度一定时,GDOP值随着纬度的增加而减小,达到某一最小值后,GDOP值便开始增加;定位点纬度一定时,GDOP值随着经度的增加而增加。分析这一趋势可知,在站台覆盖到的正向区域内,距离站台越远,GDOP值越大。

表3 基于GDOP值的定位区属性判断
试验验证所选区域内GDOP最小值为2.49,最大值为4.26,该区域内GDOP最大值小于5,根据表3所示的基于GDOP值的定位区属性判断,可知所选区域为高精度定位区,因此可利用阿尔法无线电导航系统在此区域进行导航定位。
3 结语
针对单台链双曲线定位GDOP值计算存在区域划分判定的问题,本文提出基于经度变换法的GDOP计算新方法,以此分析了阿尔法无线电导航系统在(20°N,30°E),(80°N,150°E)所围大矩形区域内的区域识别效果并计算GDOP值,并选取(29°N,103°E),(37°N,114°E)试验区域进行GDOP值计算的实验验证。仿真结果可知,经度变换法可实现定位点区域的有效识别,提升了GDOP计算的准确性和可靠性。
致谢:衷心感谢西安邮电大学陈文学、李昌兴、谢卫强和张建科4位老师在方法上和数学上提供的帮助!
[1] CHEN Shi-ru, XU Ding-jie, SUN Yao. Analysis and comparison of range-range positioning mode and hyperbolic positioning mode[J]. Journal of Marine Science and Application, 2002, 1(1): 60-64.
[2] WANG Wei, DENG Zhi-xin, ZHAO Guo-qing. Research of coastal station distribution algorithm based on GDOP in wireless positioning system[C]//IEEE International Conference on Mechatronics and Automation, Harbin: IEEE, 2007: 3150-3154.
[3] 文富忠, 董锐, 郑勇斌, 等. 远程无线电导航系统的定位误差分析及其仿真[J]. 应用科技, 2003, 30(5): 47-49.
[4] ZHONG Er-ji, HUANG Ting-zhu. Geometric dilution of precision in navigation computation[C]//International Conference on Machine Learning and Cybernetics, Dalian: IEEE, 2006: 4116-4119.
[5] 徐健, 武建锋. 附有高程约束的卫星导航系统精度因子分析方法[J]. 时间频率学报, 2018, 41(2): 120-129.
[6] 文富忠, 孙克宇, 徐定杰. 基于GDOP的导航定位误差和最优岸台设计算法的研究[J]. 哈尔滨工程大学学报, 2002, 23(2): 47-50.
[7] LEVANON N. Lowest GDOP in 2-D scenarios[J]. IEEE Proceedings-Radar, Sonar Navigation, 2000, 147(3): 149-155.
[8] KAWARMURA K, TOSHIYUKI T. Study on the improvement of measurement accuracy in GPS[C]//SICE-ICASE International Joint Conference, 2006: 1372-1375.
[9] 杨致友. 罗兰导航数学方法[M]. 西安: 西北工业大学出版社, 1991.
[10] 李彬玉, 王丰乐. 俄罗斯甚低频导航系统用于我国近海的定位精度分析[J]. 青岛大学学报(自然科学版), 2002, 15(4): 86-89.
[11] 刘睿, 朱银兵, 张婷. 中国南海区域罗兰C单台链双曲线的GDOP研究[J]. 船电技术, 2011, 31(1): 30-33.
[12] 张少泉. 有关地理纬度和地心纬度的换算问题[J]. 西北地震学报, 1985, 7(1): 39-43.
[13] 任席闯, 崔洁, 刘冰. 长河二号导航系统通信潜能分析[J]. 舰船电子工程, 2018, 38(12): 45-47.
[14] 王程峥, 李文魁, 高敬东, 等. 长河二号系统海上定位精度预测与实验研究[J]. 中国航海, 2012, 35(3): 23-26.
Single-chain hyperbolic positioning GDOP calculation based on longitude transformation method
WANG Lu-lu1,2,3, HE Zai-min1,2, HAN Zhen-xing4, HUANG Yuan-yuan1,2,3, LU Gang1,2,3
(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China;2. Key Laboratory of Time and Frequency Primary Standards, Chinese Academy of Sciences, Xi’an 710600, China;3. University of Chinese Academy of Sciences, Beijing 100049, China;4. 63768 PLA Troops, Xi’an 710600, China)
Radio hyperbolic positioning accuracy is closely related to the geometrical dilution of precision (GDOP). Since the unclear determination of region division for GDOP value calculation of single-chain hyperbolic positioning, the longitude transformation method is hence proposed, it can achieve more accurate and effective calculation of GDOP value. Using the Alpha radio navigation system as an example, the large rectangular area (20°N, 30°E), (80°N, 150°E), is calculated and analyzed. The results show that the proposed method can effectively identify the I, III and II, IV regions. In the II and IV regions, the accuracy of GDOP calculation is improved with an average of 13.07%. In the rectangular area (29°N, 103°E), (37°N, 114°E), the GDOP is less than 5, which is able to ensure the availability of test verification.
longitude transformation method; geometrical dilution of precision (GDOP); area identification; single chain; hyperbolic positioning
10.13875/j.issn.1674-0637.2020-03-0196-08
2020-01-21;
2020-04-15
中国科学院“西部之光”人才培养计划“西部青年学者”A类基金资助项目(XAB2017A05);国家自然科学基金资助项目(11703030)
王璐璐,女,硕士研究生,主要从事无线电导航与授时研究。

