参考钟对背景引力波灵敏度曲线的影响研究
刘舒,童明雷,赵成仕,李变,朱幸芝,张哲浩,韩孟纳,蒋梦源,崔广利
参考钟对背景引力波灵敏度曲线的影响研究
刘舒1,2,3,童明雷1,2,赵成仕1,2,李变1,2,朱幸芝1,2,张哲浩1,2,3,韩孟纳1,2,3,蒋梦源1,2,3,崔广利1,3,4
(1. 中国科学院 国家授时中心,西安 710600;2. 中国科学院 时间频率基准重点实验室,西安 710600;3. 中国科学院大学,北京 100049;4. 中国科学院 精密导航定位与定时技术重点实验室,西安 710600)
为了研究参考原子时标对脉冲星计时阵探测随机引力波背景的影响,我们分别使用了TA(NTSC),TT(BIPM2013)和TT(TAI)3种参考时,利用脉冲星计时处理软件Tempo2进行了模拟,又使用了国际脉冲星计时阵IPTA的真实观测数据,从计时残差数据得出每个参考时对应的积分灵敏度曲线,分别对模拟、真实数据得到的这3种灵敏度曲线进行了分析比较,该工作在脉冲星计时阵探测引力波时对于时间尺度的选择方面具有参考意义。
脉冲星;引力波;计时残差
0 引言
毫秒脉冲星的自转极其稳定,其自转周期为毫秒量级。多个单脉冲经过周期折叠可形成稳定的脉冲轮廓,测站原子钟可标记其到达时间,经过时间改正和计时模型修正,将脉冲到达望远镜的时间转换至到达太阳系质心(SSB)的时间(TOA),对应的时间尺度为太阳系质心坐标时(TCB)。根据脉冲星计时模型可以在SSB处对TOA做出预报。实际测量的TOA和预报的TOA之差称为“计时残差”。脉冲星计时可以用来进行脉冲星物理学、天体测量学、星际介质等研究。通过定期观测多颗毫秒脉冲星,可以构建脉冲星计时阵(PTA),根据各脉冲星计时残差之间的相关性可以探测宇宙中的引力波。PTA主要目的之一是探测各向同性、随机的引力波背景(GWB)[1],GWB是由一群质量为107~109倍太阳质量的双黑洞在旋进阶段产生的,处于纳赫兹频段。由于处于该频段中的大多数引力波源无法分解开来,它们各自发出的引力波信号互相叠加,从而形成GWB。
国际上,自从Advanced LIGO[2]宣布直接探测到引力波事件GW150914,Advanced LIGO又陆续观测到了许多双黑洞的并合。2017年8月17日,Advanced LIGO[3]和Advanced Virgo[4]还联合探测到了双中子星系统GW170817产生的巨磁阻。此外,最近LIGO和Virgo宣布探测到一个双星合并的引力波事件S190814bv[5],误报率约为每1.6×1025a一次,99%的概率为中子星-黑洞合并。
近年来,利用单颗脉冲星或脉冲星阵列来限制、探测GWB,在理论方面取得了长足的进展[6-9],对引力波幅度的限制在不断加强。目前对超大质量双黑洞的随机、各向同性GWB的振幅幅值的最佳限制来自R. W. Shannon[10],该文章限制GWB的幅度上限为10-15。另外,童明雷等[11]分析了引力波引起额外脉冲星计时残差的过程。
本文通过对PTA数据的分析,探究了不同参考时间标准对探测GWB的影响。我们使用了脉冲星计时处理软件Tempo2,在不同的参考钟条件下,得到不同的计时残差。通过分析这些计时残差的特征,构建出相应的引力波积分灵敏度曲线,有利于研究参考钟误差对脉冲星计时阵探测引力波的影响,从而选择更优质的参考时间。Tempo2是较为精确的脉冲星计时处理软件,从地球时间(TT)转换到TCB精度优于1 ns。关于Tempo2的详细介绍可参阅文献[12-13]。考虑到对太阳系行星历表误差建立模型较困难,本文采用了喷气推进实验室(JPL)公布的历表DE421。另外,由于真实观测数据中存在各类红噪声,分析起来较复杂,为了更真实地反映仅参考原子时引起的GWB探测误差,我们分别使用模拟数据、真实观测数据进行分析。
1 模拟数据分析
脉冲星的TOA测量依赖于参考时间,一般参考由国际原子时(TAI)修正得到、国际权度局BIPM(Bureau International des Poids et Measures)每年计算公布的地球时TT(BIPM),对所有脉冲星而言,参考时间误差对计时残差的影响是相同的(即单极性的),并将影响每颗脉冲星的模型参数拟合结果。与单极性的参考时钟误差不同,GWB对计时残差的影响是四极性的,但单极性的时钟误差仍然是影响PTA探测GWB的一个因素,即时钟误差构成了GWB探测中的一个误差来源[14-15],另外,PTA探测引力波的灵敏度通常由引力波和噪声的功率谱密度之比描述,但是对于在探测器频带中具有幂律频率相关性的随机引力波,为了说明随着频率积分而引起的灵敏度提高,E. Thrane等[16]提出了一种积分灵敏度曲线。下面我们将通过模拟的脉冲星计时数据重点讨论参考时钟误差对GWB积分灵敏度曲线的影响。
本文以Parkes脉冲星计时阵列公开数据1(PPTA DR1)的17颗毫秒脉冲星为研究对象。在模拟过程中,我们将脉冲星总观测时间设定为13 a;为了降低模拟过程的工作量,我们将观测间隔统一取为每两周观测一次;每颗脉冲星的原始的计时模型参数作为输入,生成标准模拟TOA,然后对于所有脉冲星,将参考时标分别设置为中国科学院国家授时中心地方原子时(TA(NTSC))、BIPM2013年发布的地球时(TT(BIPM2013))以及由TAI实现的地球时(TT(TAI))。改变参考时标后,对计时模型参数进行再次拟合,生成相应的拟合后计时残差。不同参考时标对应的拟合后计时残差,是构建GWB积分灵敏度曲线的基础。接下来我们首先分析TOA的不确定度,即模拟TOA的白噪声为100 ns时的积分灵敏度曲线。
1.1 模拟白噪声为100 ns时的情况
脉冲星计时数据所参考的时钟时间系统应具有良好的长期稳定性,没有频率漂移或周期性变化,应与SI秒一致。TAI系统是一个由世界各地重点实验室加权的近实时系统。BIPM每年对大量守时资料进行事后重新处理,进而得到TT(BIPM),与TAI相比,TT(BIPM)频率稳定性与准确性都有所提高,对目前脉冲星计时而言,是最合适的参考时标。附录中图5给出了TT(TAI)与TT(BIPM2013)的差值随着时间的变化。
中国科学院国家授时中心负责我国国家时间/频率基准的建立与保持,2016年对TAI归算的权重贡献约5.5%,排在全球守时实验室的第4位,为全球最重要的守时实验室之一。地方原子时TA(NTSC)由NTSC的守时钟组(铯原子钟和氢原子钟组成)经精密比对和计算后实现。目前,原子时TA(NTSC)的频率稳定度优于10-14/(5 d),TAI在30 d时的频率稳定性优于4×10-16。UTC(NTSC)是我国的标准时间,自2015年以来与UTC的偏差保持在±10 ns之内。
为了研究不同参考时钟对探测GWB灵敏度的影响,我们将模拟的脉冲到达时间的不确定度设定为100 ns(由此产生的拟合后计时残差见表1),参考钟分别采用TA(NTSC),TT(BIPM2013)和TT(TAI)进行了实验研究,得到图1所示的灵敏度曲线。在这里,TT(TAI)与TAI的差值是一个常量:TT(TAI)=TAI+32.184s。结果表明,TT(BIPM2013)的积分灵敏度曲线位于最下方,即探测背景引力波的能力最强,基于TT(TAI)的灵敏度曲线与基于TT(BIPM2013)的灵敏度曲线最为接近。
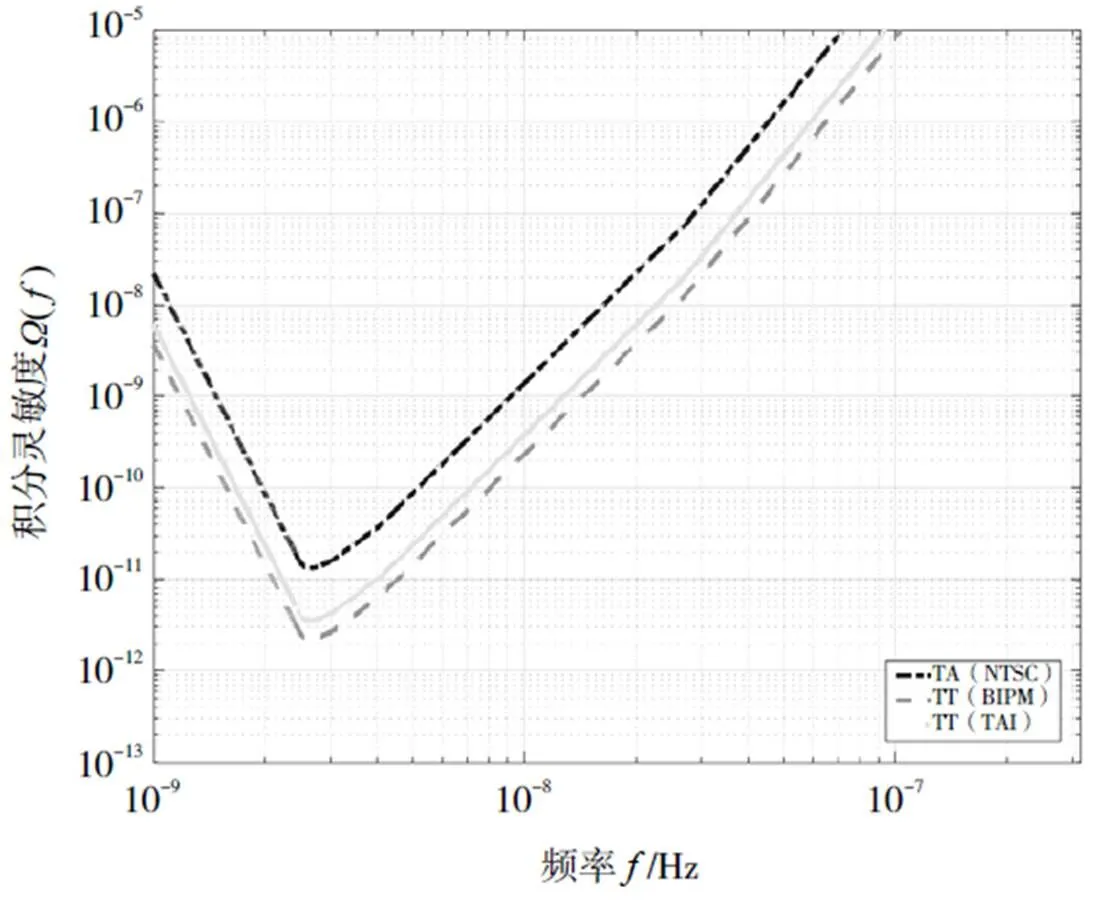
图1 TOA的不确定度统一设定为100 ns时的积分灵敏度曲线
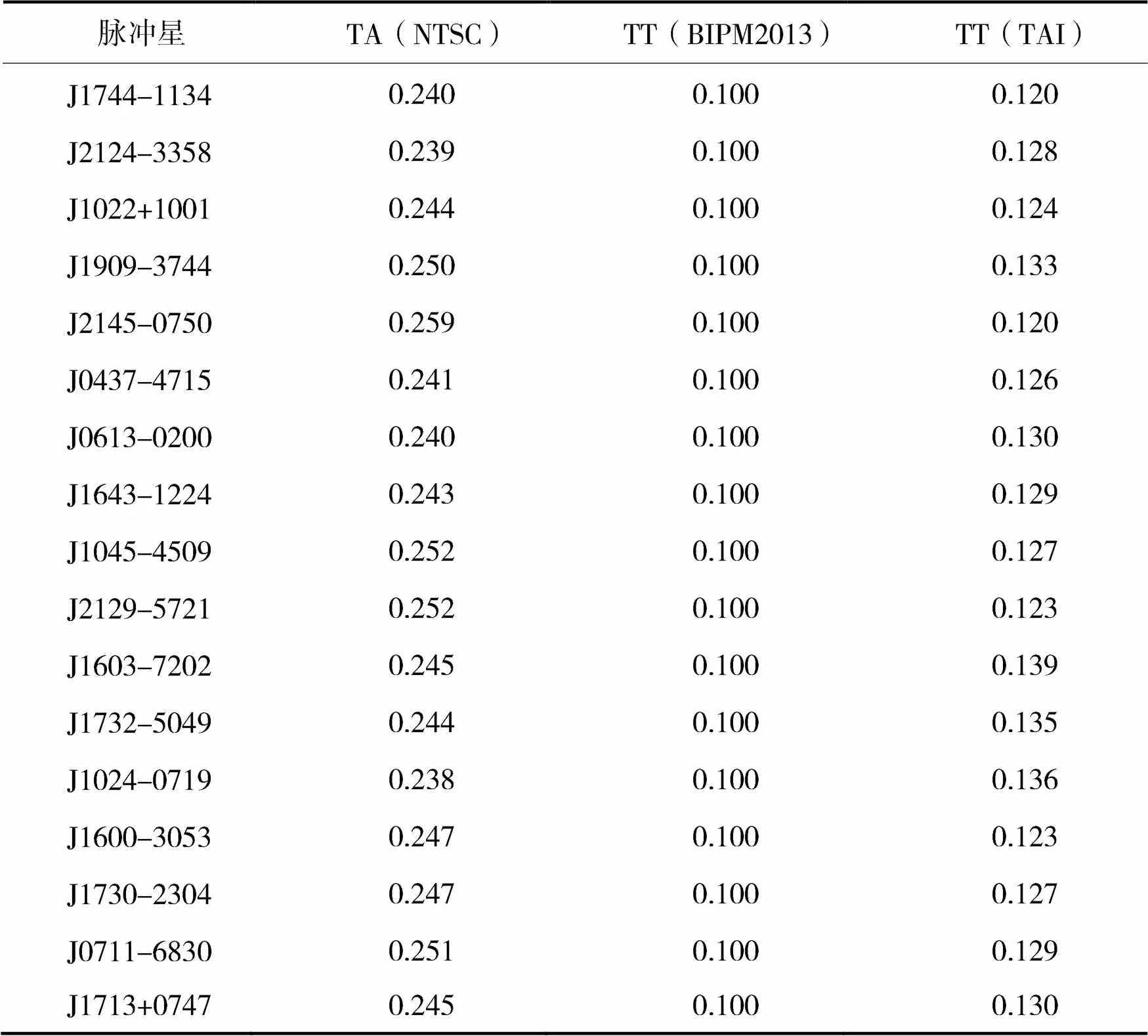
表1 模拟白噪声为100 ns时,不同地方原子时对应的计时残差的均方根 单位:µs
1.2 模拟白噪声与真实数据计时残差均方根相同的情况
我们将模拟的TOA的不确定度设定为与每颗星的真实观测数据计时残差相同(真实的计时残差如表2),参考钟分别采用TA(NTSC),TT(BIPM2013)和TT(TAI)进行了实验研究,结果如图2所示。结果表明,TT(BIPM2013)的积分灵敏度曲线位于最下方,探测背景引力波的能力最强,基于 TT(TAI)参考时的灵敏度曲线与基于TT(BIPM2013)的灵敏度曲线最为接近。
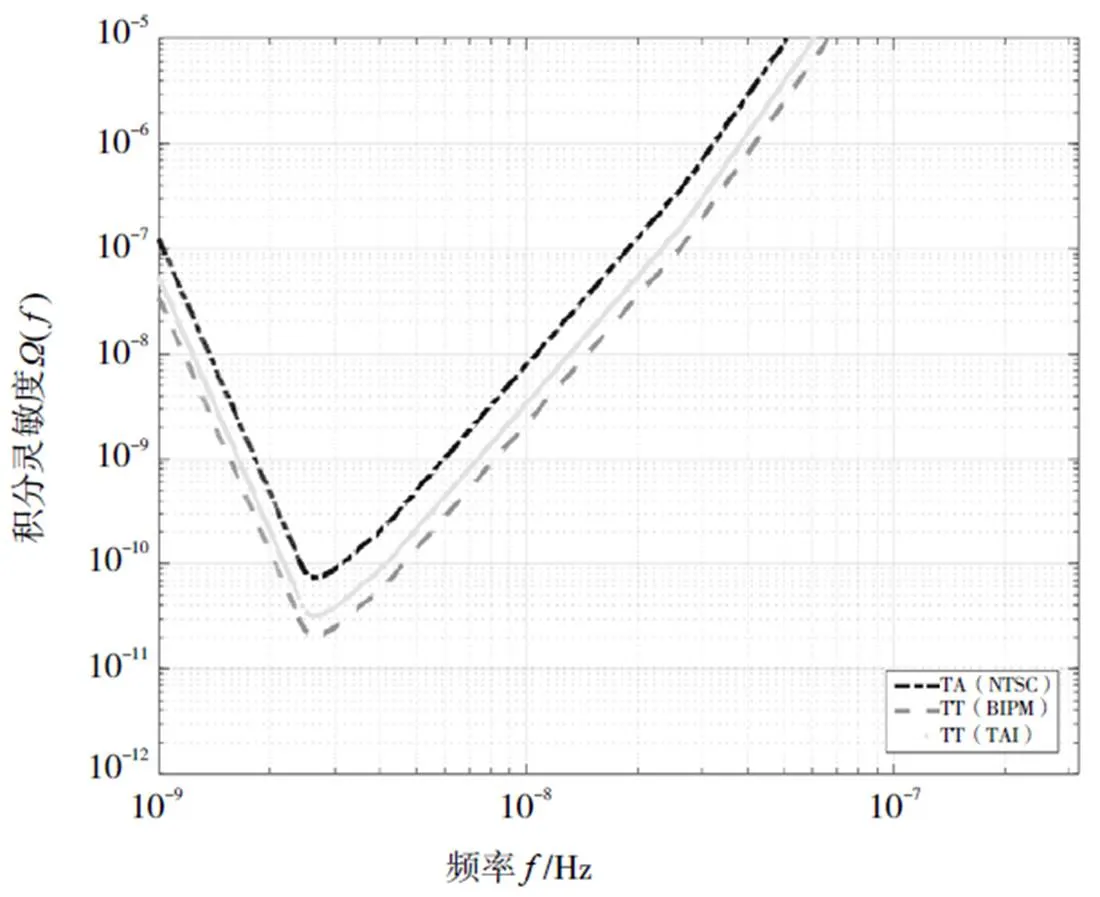
图2 模拟TOA的不确定度与真实观测数据相同时的积分灵敏度曲线

表2 模拟TOA的不确定度与真实观测数据相同时,不同地方原子时对应的计时残差的均方根 单位:µs
2 真实数据分析
以上用模拟数据分析的积分灵敏度曲线只包含白噪声的影响,然而,在实际数据中总存在红噪声。我们根据实际观测资料分析了参考时对灵敏度曲线的影响效应。我们以从国际脉冲星计时阵列数据发布1(IPTA DR1)中选取的7颗毫秒脉冲星为研究对象,总观测时间跨度为13 a,对于所有脉冲星,参考时钟分别被设置为TA(NTSC),TT(BIPM2013)和TT(TAI)。当参考时间尺度改变时,需要重新拟合计时模型参数,形成相应的拟合后计时残差(由此产生的拟合后计时残差见表3)。不同时间参考的脉冲星的拟合后计时残差成为开始分析的基本数据。
为了验证钟的二次项以内的漂移并不影响引力波探测,我们生成了均值为0的二次多项式,并将其加入至TAI的钟差文件中,对脉冲星的真实观测数据进行拟合,结果表明,二次项以内的钟的漂移并不影响Tempo2的拟合结果,即并不影响引力波的探测。TAI钟差加上某均值为0的二次项与TAI钟差的对比,如图3所示。
引力波积分灵敏度曲线如图4。结果表明,TT(BIPM2013)的积分灵敏度曲线位于最下方,探测背景引力波的能力最强,TT(TAI)次之,且TT(TAI)与TT(BIPM2013)探测引力波能力接近,而此时TA(NTSC)探测引力波能力较低,与理论预期一致。
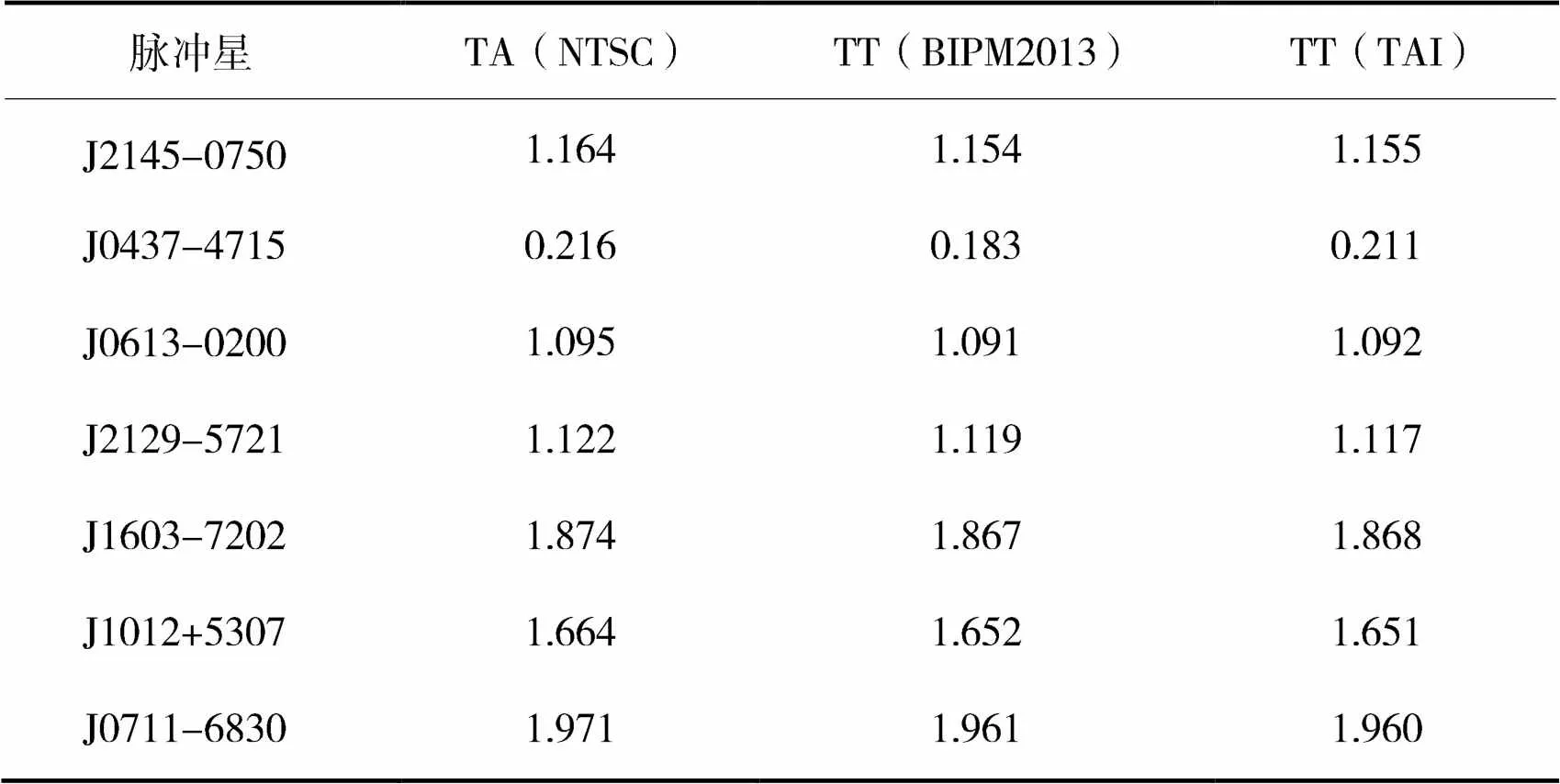
表3 使用真实观测数据时,不同地方原子时对应的计时残差的均方根 单位:µs
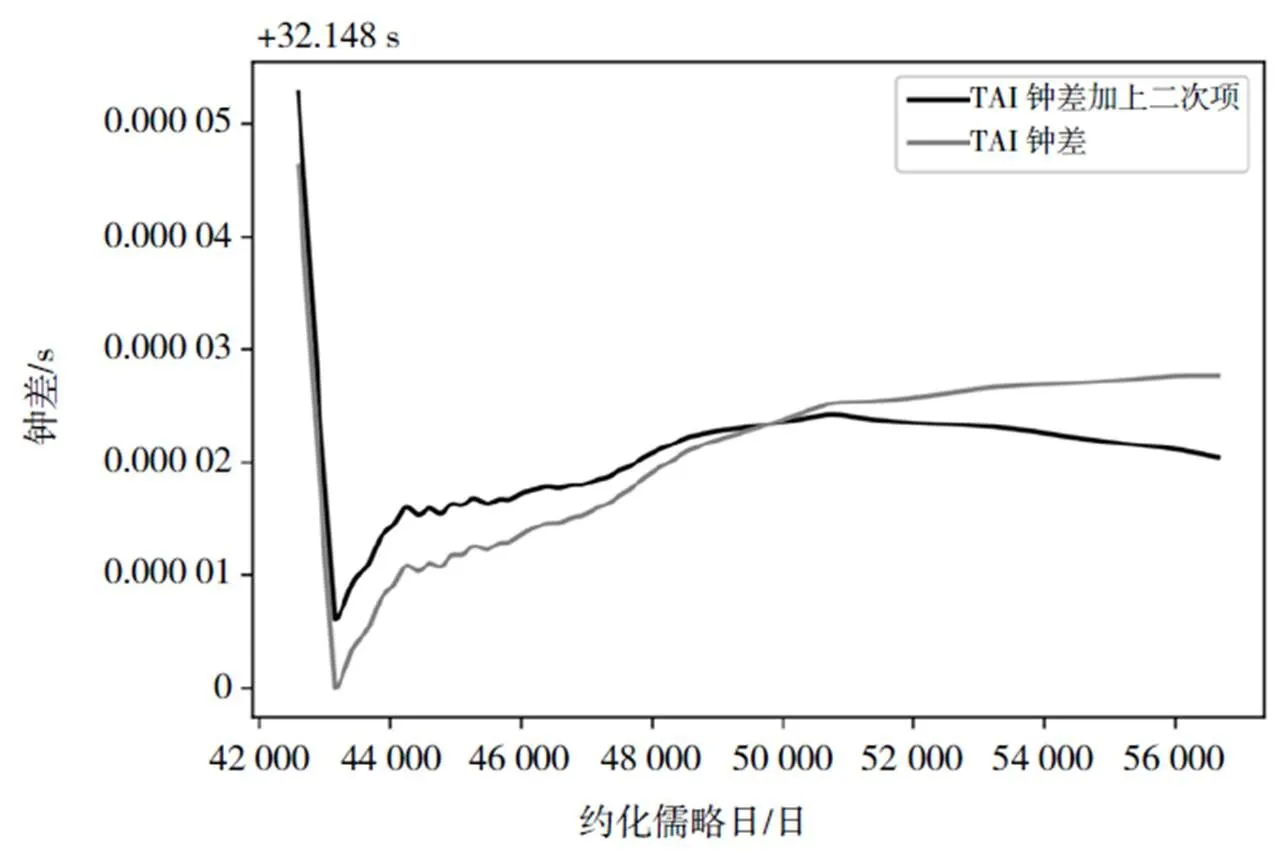
图3 TAI钟差曲线和加上二次项后的漂移曲线
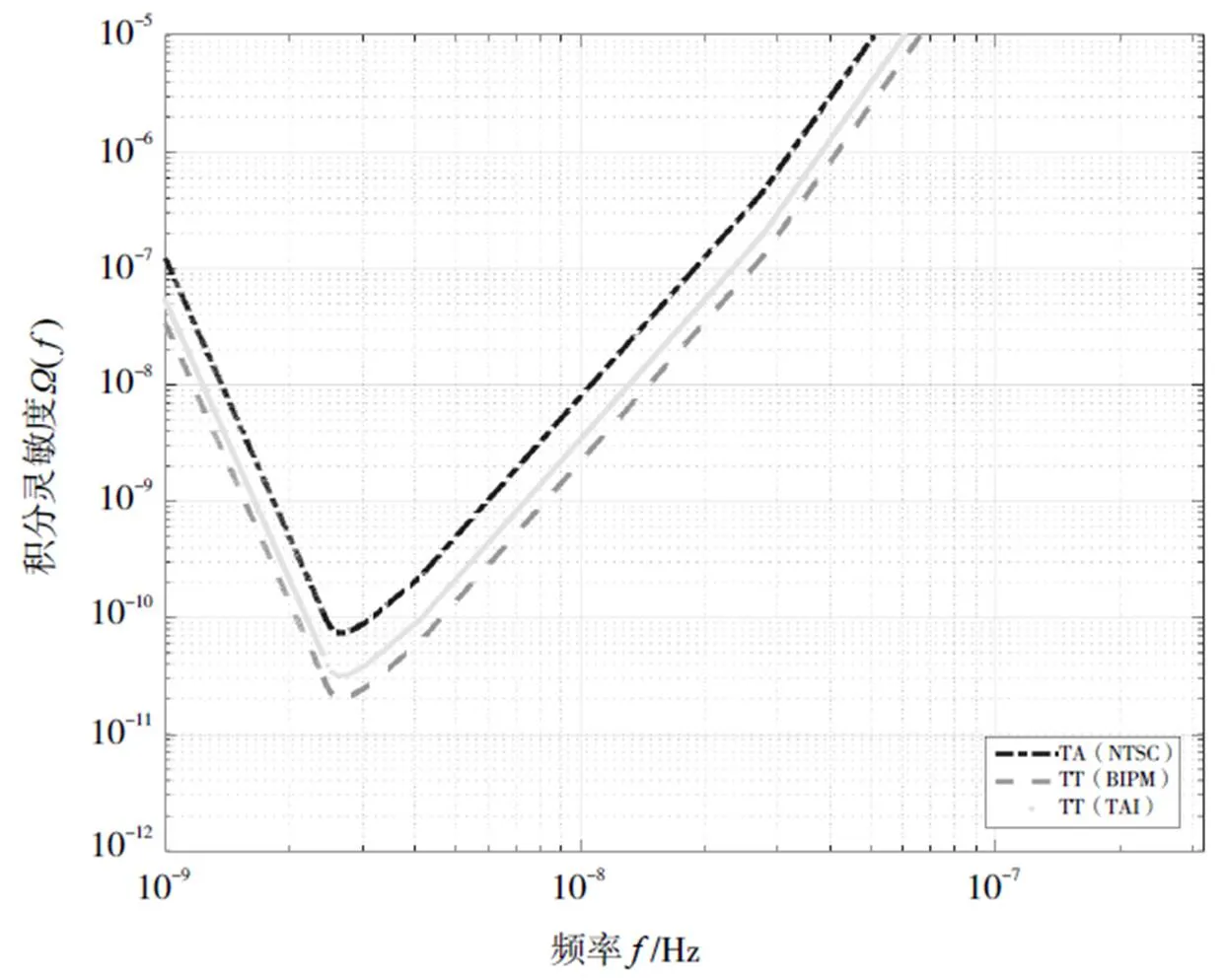
图4 真实观测数据的积分灵敏度曲线
3 结语
基于GWB的幂律积分灵敏度曲线,我们讨论了参考时引起的相关噪声对探测GWB的影响,分别从模拟数据和真实数据对3种不同参考原子时标对应的积分灵敏度曲线进行了分析。结果表明,以 TT(BIPM2013)代替TT(TAI)作为参考时间标度,灵敏度会显著提高。由于TAI参考了由世界各地76个实验室的500多个原子钟,是准实时实现的最稳定的原子时间尺度。即使如此,如果用事后处理版本TT(BIPM2013)作为参考时间,幂律积分灵敏度仍有显著提高。因此我们认为,参考时钟误差对探测GWB的影响是不可忽略的。其次,我们分析了地方原子时TA(NTSC)的影响。我们发现在模拟数据中,基于TA(NTSC)的灵敏度曲线会比基于TT(BIPM2013)的灵敏度曲线差0.5~1个数量级,与在真实观测数据中一致。我们认为,随着脉冲星计时精度的快速提高,选择合适的参考原子时间尺度将成为影响脉冲星计时阵探测GWB的一个重要因素,在真实观测数据中,更精确的参考时标会越来越重要。
[1] HELLINGS R W, DOWNS G S. Upper limits on the isotropic gravitational radiation background from pulsar timing analysis[J]. The Astrophysical Journal, 1983, 265: 39-42.
[2] ABBOTT B P, ABBOTT R, ABBOTT T D, et al. Observation of gravitational waves from a binary black hole merger[J]. Physical Review Letters, 2016, 116: 061102.1-061102.16.
[3] AASI J, ABBOTT B P, ABBOTT R, et al. Advanced LIGO[J].Classical Quantum Gravity, 2015, 32: 074001.
[4] ACERNESE F, AGATHOS M, AGATSUMA K, et al. Advanced Virgo: a second-generation interferometric gravitational wave detector[J]. Classical Quantum Gravity, 2015, 32(2): 024001.
[5] LIGO Scientfic Collaboration, Virgo Collaboration. LIGO/Virgo S190814bv: identification of a GW compact binary merger candidate[J]. International Journal of Future Generation Communication and Networking, 2019, 25324: 1.
[6] DEMOREST P B, FERDMAN P B, GONZALEI M E, et al. Limits on the stochastic gravitational wave background from the north American nanohertz observatory for gravitational waves[J]. The Astronomical Journal, 2013, 762(2): 94-118.
[7] JENET F A, HOBBS G B, STRATEN W V, et al. Upper bounds on the low-frequency stochastic gravitational wave background from pulsar timing observations: current limits and future prospects[J]. The Astronomical Journal, 2006, 653(2): 1571-1576.
[8] KASPI V M, TAYLOR J H, RYBA M F, et al, High-precision timing of millisecond pulsars. 3: long-term monitoring of PSRs B1855+09 and B1937+21[J]. The Astronomical Journal, 1994, 428: 713-728.
[9] MCHUGH M P, ZALAMANSKY G, VERNOTTE F, et al. Pulsar timing and the upper limits on a gravitational wave background: a bayesian approach[J]. Physical Review D, 1996, 54: 5993-6000.
[10] SHANNON R M, RAVI V, LENTATI L T, et al. Gravitational waves from binary supermassive black holes missing in pulsar observations[J]. Science, 2015, 349: 1522-1525.
[11] 童明雷, 丁勇恒, 赵成仕, 等. 引力波引起的脉冲星计时残差模拟与分析[J]. 时间频率学报, 2015, 38(1): 44-51.
[12] HOBBS G B, EDWARDS R T, MANCHESTER R N. TEMPO2: a new pulsar-timing package-I. an overview[J]. Monthly Notices of the Royal Astronomical Society, 2006, 369(2): 655-672.
[13] EDWARDS R T, HOBBS G B, MANCHESTER R N. TEMPO2: a new pulsar-timing package II. the timing model and precision estimates[J]. Monthly Notices of the Royal Astronomical Society, 2006, 372(4): 1549-1574.
[14] HOBBS G B, COLES W, MANCHESTER R N, et al. Development of a pulsar-based time-scale[J]. Monthly Notices of the Royal Astronomical Society, 2012, 427(4): 2780-2787.
[15] TIBURZI C, HOBBS G, KERR M, et al. A study of spatial correlations in pulsar timing array data[J]. Monthly Notices of the Royal Astronomical Society, 2015, 455(4): 4339-4350.
[16] THRANE E, ROMANO J D. Sensitivity curves for searches for gravitational-wave backgrounds[J]. Physical Review D, 2013, 88(12): 124032.1-124032.11.
附录
图5中把TT(BIPM2013)作为没有误差的理想时间尺度,给出了TT(TAI)与TT(BIPM2013)从1975年至2013年38a内时域上的差值(图5(a))。可以清晰看出,在过去的30多年,TT(TAI)漂移了近30μs,呈现了明显的二次曲线变化,去除了该变化之后,结果仍然出现了近似抛物线变化,幅度在-5~3 μs之间(图5(b)),这是由原子频标的二次漂移项引起的。从整体变化看,TT(TAI)与TT(BIPM2013)的差异随着时间的增长在逐渐增大。这表明TAI所实现的秒长虽然经过了一级频标的频率修正,但频率的准确性仍然存在不足,TAI的频率修正原则需要进一步改进。

图5 TT(TAI)与TT(BIPM2013)的差值随着时间的变化
Research on the effect of referenced clocks on the sensitivity curve of gravitational wave backgrounds
LIU Shu1,2,3, TONG Ming-lei1,2, ZHAO Cheng-shi1,2, LI Bian1,2, ZHU Xing-zhi1,2,ZHANG Zhe-hao1,2,3, HAN Meng-na1,2,3, JIANG Meng-yuan1,2,3, CUI Guang-li1,3,4
(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China;2. Key Laboratory of Time and Frequency Primary Standards, Chinese Academy of Sciences, Xi’an 710600, China;3. University of Chinese Academy of Sciences, Beijing 100049, China;4. Key Laboratory of Precise Positioning and Timing Technology, Chinese Academy of Sciences, Xi’an 710600, China)
In order to study the effect of referenced clocks on the detection of the stochastic gravitational wave backgrounds using pulsar timing arrays, we used three local atomic clocks, TA(NTSC), and TT(BIPM 2013), and TT(TAI), then simulated them using the pulsar timing processing software Tempo2. And we analyzed the real observation data from the International Pulsar Timing Array(IPTA). The integrated sensitivity curves corresponding to all clocks were obtained from the timing residual, and sensitivity curves obtained from simulated and real data are analyzed and compared. This work provides a significant reference for the selection of time scale on the detection of gravitational waves using pulsar timing array.
pulsar; gravitational wave; timing residual
10.13875/j.issn.1674-0637.2020-03-0214-08
2020-01-17;
2020-04-09
国家自然科学基金资助项目(U1831130;U1531112);中国科学院青年创新促进会资助项目(2017450);国家自然科学基金面上资助项目(11873049)
刘舒,女,硕士,主要从事脉冲星计时探测引力波研究。

