脉冲星计时中噪声对稳定度的影响分析
张哲浩,童明雷,赵成仕,朱幸芝,刘舒,韩孟纳
脉冲星计时中噪声对稳定度的影响分析
张哲浩1,2,3,童明雷1,2,赵成仕1,2,朱幸芝1,2,刘舒1,2,3,韩孟纳1,2,3
(1. 中国科学院 国家授时中心,西安 710600;2.中国科学院 时间频率基准重点实验室,西安 710600;3. 中国科学院大学,北京 100049)
脉冲星计时中存在多种噪声,使得建立的脉冲星时稳定度受到不同程度的影响。首先利用模拟数据,分别给出了白噪声和脉冲星自转不稳定引起的计时红噪声对脉冲星时稳定度的影响。结果表明脉冲星时稳定度受计时红噪声的影响特征与理论预期一致。同时,我们采用国际脉冲星计时阵第一批发布的数据,研究了各种模型参数改正和噪声改正对脉冲星时稳定度的影响,发现计时模型参数与色散变化的影响要远大于白噪声改正。此外,通过与模拟数据的分析相比较,验证了经过各种改正后真实数据中噪声的复杂性,简单的功率谱模型并不能完全描述残差中的红噪声。
脉冲星计时;计时噪声;脉冲星时;稳定度
0 引言
脉冲星是宇宙中一种自转非常稳定的致密天体,按自转周期的长短可以分为普通脉冲星与毫秒脉冲星。毫秒脉冲星的长期稳定度甚至可以和原子时匹敌,对这类天体的观测可以构建脉冲星时[1-2],并有望成为未来守时的重要组成部分[3]。获得脉冲星时间信号的过程被称为脉冲星计时(pulsar timing),首先通过望远镜接收来自星体的辐射获得脉冲轮廓,然后与标准脉冲轮廓做相关来确定脉冲到达时间(times of arrival,TOA),而TOA是由参考原子时记录的。确定TOA的过程实际上是原子时与脉冲星时的时间比对过程。将这些实际测量的TOA与基于计时模型理论预报的TOA相比较,两者之差即为计时残差,使用最小二乘法优化残差即可以更新计时模型[4-6]。由于脉冲星的自转以及信号传播受到许多因素的干扰,观测得到的TOA总是与计时模型计算所得的理论值存在差异,从而计时残差总不为零,或者说残差中存在着噪声。计时残差中的噪声对脉冲星在守时理论,深空导航以及引力波探测等方面的应用产生了根本的影响,因为这些应用都基于对残差信号的分析[7]。
从广义的角度讲,任何非模型化因素引起的残差都可被称为噪声。残差中的噪声按功率谱分为两类:白噪声与红噪声。白噪声源自大量随机因素的影响,这些随机因素在脉冲信号产生,传播以及接收中随处可见。对于脉冲星时而言,可以将多颗星的残差综合并处理从而降低噪声水平[1]。随着测量时间跨度的不断增加,白噪声对模型参数拟合的影响也会逐渐降低[8]。红噪声则不同,随着测量时间跨度的增加,它会在计时残差中逐渐显现并破坏残差的稳定度,进而干扰模型参数的确定。J. P. W. Vebiest[9], G.Hobbs[10]以及W.A.Coles等人[11]曾提出不同的方法用于解决红噪声条件下的计时模型拟合问题,G.Hobbs与W.A.Coles的方法已被模块化为脉冲星计时软件Tempo2①http://www.atnf.csiro.au/research/pulsar/tempo2的一部分。同时,A.E.Rodin[12], G.Hobbs等[13]研究了相应的算法以降低红噪声对脉冲星时稳定度的影响。由于红噪声的来源广泛,产生机制复杂,寻求有效的处理方法仍是一个问题。历史上很多学者提出过各种噪声模型用于评估红噪声,如J.M.Cordes和D.J.Helfand[14]使用拟合后计时残差中红噪声成分的均方根反映噪声的大小,具体某颗星的噪声水平通过与Crab脉冲星的噪声相比而得到。A. Arzoumanian[15]提出使用自转频率以及频率的二阶导数评估噪声水平,这种方法对时间跨度有一定的要求,且频率的二阶导数很小时也不适用。 R. M. Shannon[16]的方法使用拟合后计时模型的自转频率,频率导数和数据的时间跨度作为评估量,文献[17]曾使用这种模型对Parkes脉冲星数据库中脉冲星的噪声进行过评估。与此同时,人们也对红噪声的起源提出过各种猜想,如S. M. Kopeikin[18]根据散射噪声理论将脉冲星自转噪声分为随机游走噪声与闪烁噪声,并据此证明噪声平稳部分的功率谱为幂律形式。
对于脉冲星时而言,稳定度是最为重要的特性之一。影响脉冲星时稳定度的因素有很多,例如参考原子时误差、太阳系历表误差以及引力波等[19]。本文主要讨论各种计时噪声对脉冲星时稳定度的影响。首先使用模拟数据研究白噪声与自转红噪声(脉冲星自转的不稳定)对稳定度的影响,而后分析真实数据中参数改正对稳定度的影响,其中真实数据使用国际脉冲星计时阵(International Pulsar Timing Array,IPTA)第一批发布的数据[20]。
1 IPTA的噪声模型
在脉冲星计时观测中,白噪声可以归结于两种噪声源[20],其一是反映观测设备随机影响的辐射计噪声,它被表述为
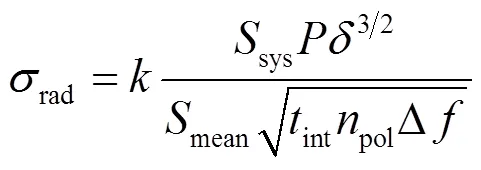
另一种噪声源—相位抖动噪声,被表示为


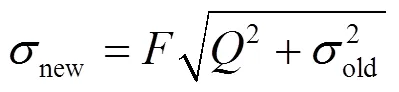
与白噪声相比,红噪声的种类更加复杂[21]。脉冲星计时中的红噪声包括脉冲星的自转红噪声,色散(dispersion measure,DM)变化导致的噪声,观测设备噪声以及某一频带下的噪声。IPTA发布的数据对自转红噪声使用功率谱模型描述[11]
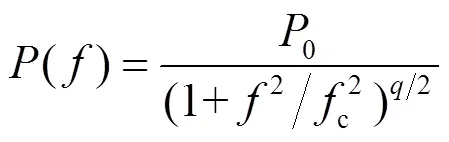
式(4)中,代表红噪声的强度,为傅立叶频率,是转折频率,为谱指数。图1展示了某一参数改变对该模型功率谱曲线的影响。越大,谱密度在低频段的强度越大;转折频率与谱指数共同确定曲线的拐点,当频率大于(小于)拐点时,谱密度的二阶导数大于(小于)0;则反应了曲线的陡峭程度,越大,谱密度随频率增加而下降得越快。
对于DM变化以及系统与频带噪声,IPTA发布的数据也给出了模型参数。由星际介质色散造成的脉冲延迟被表示为
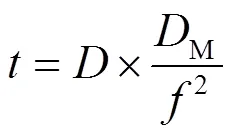
2 脉冲星时的稳定度
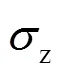
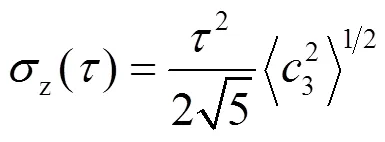


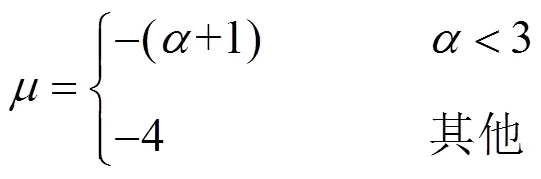
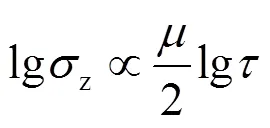
对应S.M.Kopeikin[18]提出的噪声理论,使用式(7)表示脉冲星计时中常见的红噪声时,的取值范围为-4~1,考虑到白噪声,式(10)中对数曲线(这里是直线)的斜率范围为-1.5~1.5(如图2所示,均为整数),这从理论上给出了曲线在不同噪声下随测量区间长度的变化情况。≥3时曲线斜率恒为-2,>2的(高频)噪声在脉冲星计时中并未发现。当-1<≤2(=2对应白噪声)时,虽然存在红噪声,稳定度仍随着观测时间的增加而提高。<-1时,随着观测时间的增加,稳定度越来越差。
3 模拟数据分析噪声对稳定度的影响
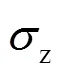

图3 只含有白噪声的模拟数据计算所得的
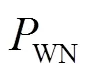
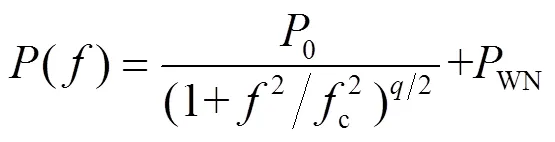
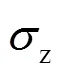
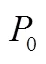
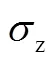
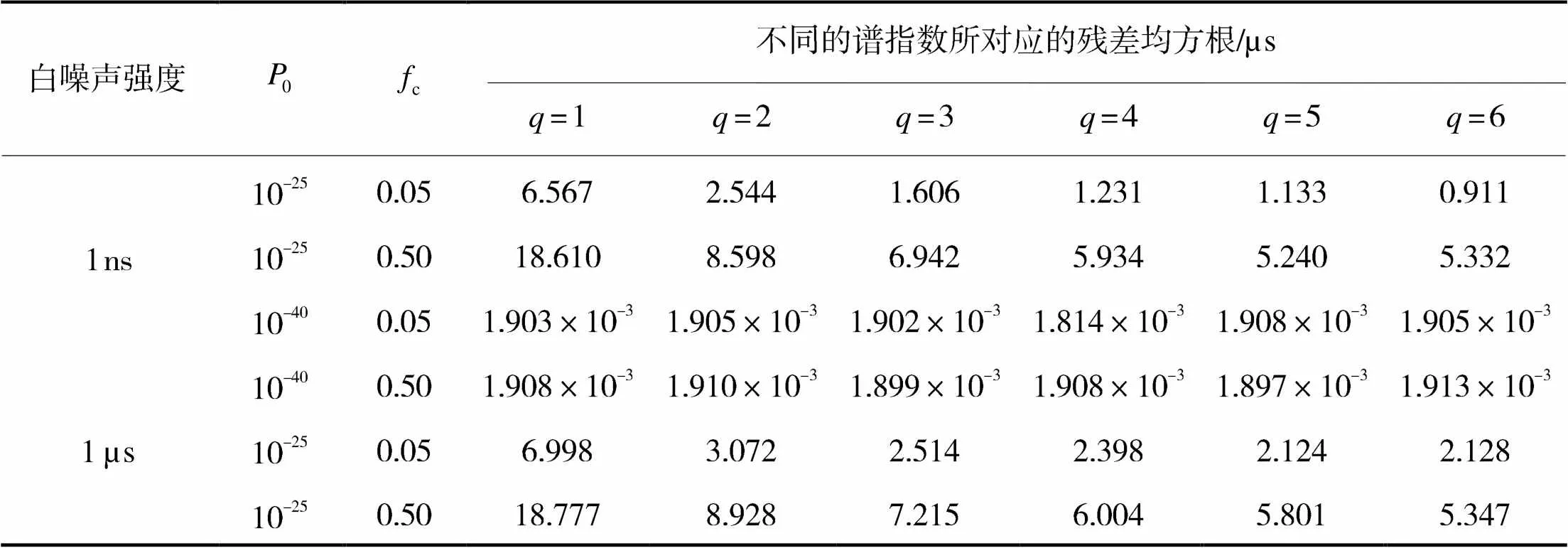
表1 不同类型噪声下残差的均方根
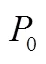
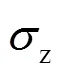
4 真实数据中参数改正对稳定度的影响
真实数据的噪声特性比模拟数据复杂得多,而且真实数据的分布与不确定度也具有随机性,这使得相同噪声对真实数据与模拟数据稳定度曲线的影响存在差异。在研究中,我们着重考虑参数改正对稳定度造成的影响。
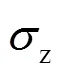
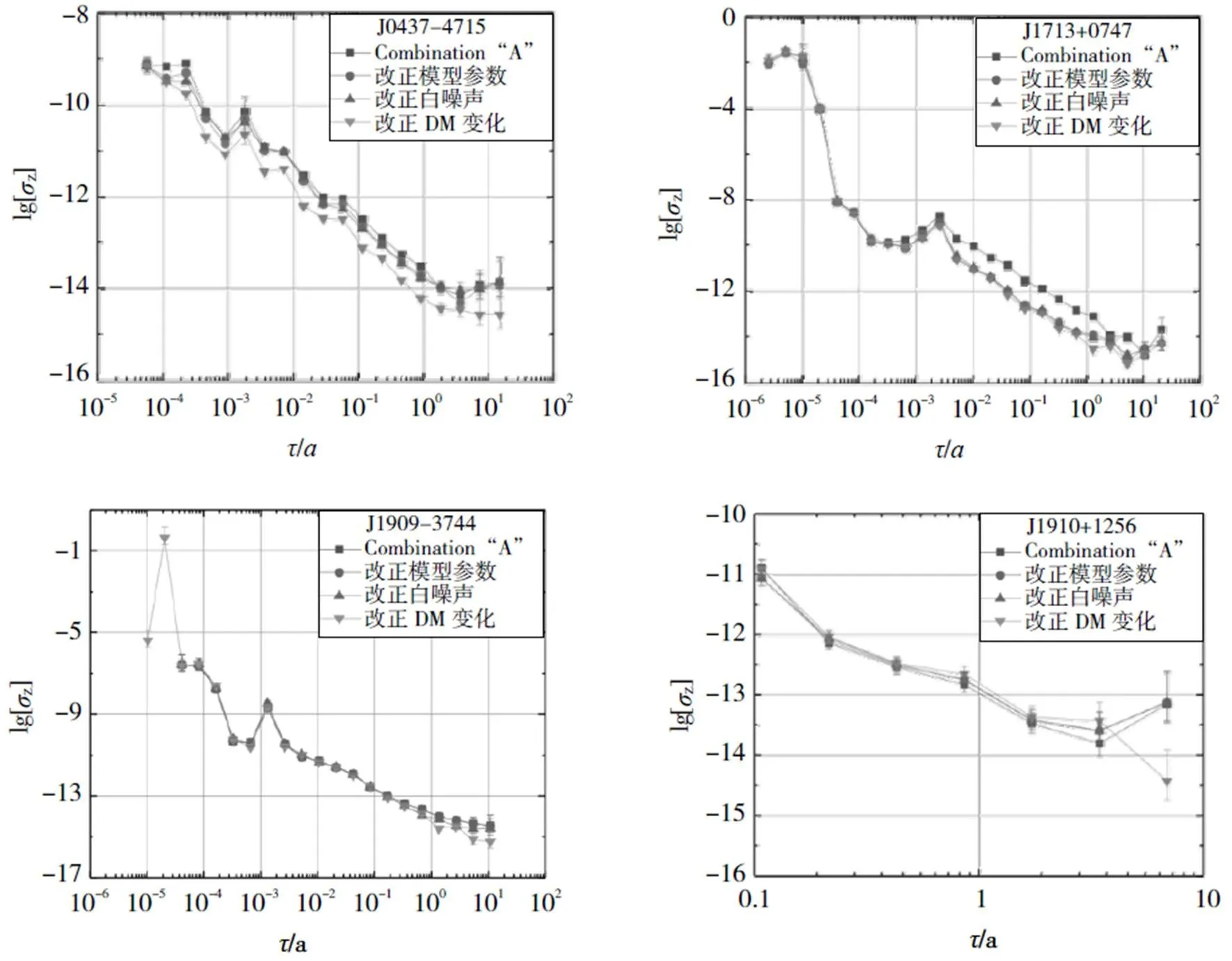
图5 从Combination“A”到Combination“B”数据转换中不同参数改正对残差的稳定度曲线的影响

表2 IPTA给出的真实数据的红噪声模型参数以及从Combination“A”到Combination“B”改正过程中残差的WRMS
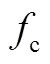
5 结语
[1] PETIT G,TAVELLA P. Pulsars and time scales[J].Astronomy and Astrophys,1996,308(1):290-298.
[2] ILYASOV YP,KOPEIKIN SM,RODIN AE. The astronomical timescale based on the orbital motion of a pulsar in a binary system[J].1998,24(2):228-236.
[3] PíRIZ R,GARBIN E, ROLDáN P,et al. PulChron: a pulsar time scale demonstration for PNT systems[C] // 50th Annual Precise Time and Time Interval System and Applications Meeting, Virginia: ION, 2019.
[4] HOBBS GB,EDWARDS RT,MANCHESTER RN. Tempo2,a new pulsar-timing package-I.An overview[J]. Monthly Notices of the Royal Astronomical Society,2006,369(2):655-672.
[5] LORIMER DR,KRAMER M. Handbook of Pulsar Astronomy[M].Cambridge: Cambridge University Press,2005.
[6] EDWARDS RT,HOBBS GB,MANCHESTER RN. TEMPO2,a new pulsar-timing package-II.The timing model and precision estimates[J]. Monthly Notices of the Royal Astronomical Society,2006,372:1549-1574.
[7] BECKER W,KRAMER M,SESANA A. Pulsar timing and its application for navigation and gravitational wave detection[J]. Space Science Review,2018,214(1): 1-25.
[8] KOPEIKIN,SERGEI M. Millisecond and binary pulsars as nature’s frequency standards-II.The effects of low-frequency timing noise on residuals and measured parameters[J]. Monthly Notices of the Royal Astronomical Society,1999,305(3): 563-590.
[9] VERBIEST JPW, BAILES M, COLES W A, et al. Timing stability of millisecond pulsars and prospects for gravitational-wave detection[J]. Monthly Notices of the Royal Astronomical Society,2009,400: 951-968.
[10] HOBBS G,LYNE AG,KRAMER M,et al. Long-term timing observations of 374 pulsars[J]. Monthly Notices of the Royal Astronomical Society,2004,353:1311-1344.
[11] COLES WA,HOBBS G,CHAMPION DJ,et al. Pulsar timing analysis in the presence of correlated noise[J]. Monthly Notices of the Royal Astronomical Society,2011,418(1):561-570.
[12] RODIN AE. The optimal filters for the construction of the ensemble pulsar time[J]. Monthly Notices of the Royal Astronomical Society,2008,387(4):1583-1588.
[13] HOBBS GB,COLES W A.MANCHESTER RN,et al. Development of a pulsar-based time-scale[J]. Monthly Notices of the Royal Astronomical Society,2012,427(4):2780-2787.
[14] CORDES JM, HELFAND DJ. Pulsar timing Ⅲ.Timing noise of 50 pulsars[J]. The Astrophysical Journal, 1980,239:640-650.
[15] ARZOUMANIAN A,NICE DJ,TAYLOR JH,et al. Timing behavior of 96 radio pulsars[J]. The Astrophysical Journal, 1994,422:671-680.
[16] SHANNON RM,CORDES JM. Assessing the role of spin noise in the precision timing of millisecond pulsars[J]. The Astrophysical Journal, 2010, 725(2):1607-1619.
[17] 杨廷高, 童明雷, 高玉平. 毫秒脉冲星计时噪声估计[J]. 时间频率学报, 2014, 37(2): 80-88.
[18] KOPEIKIN S M. Millisecond and binary pulsars as nature’s frequency standards-I.A generalized statistical model of low-frequency timing noise[J]. Monthly Notices of the Royal Astronomical Society, 1997, 288: 129-137.
[19] 丁勇恒, 童明雷, 赵成仕. 影响脉冲星时稳定度的因素分析[J].时间频率学报, 2017, 40(4):260-267.
[20] VERBIEST JPW,LENTATI L,HOBBS GB,et al. The international pulsar timing array: first data release[J]. Monthly Notices of the Royal Astronomical Society,2016,458(2):1267-1288.
[21] OSLOWSKI S, STRATEN WV,HOBBS GB,et al. High signal-to-noise ratio observation and the ultimate limits of precision pulsar timing[J]. Monthly Notices of the Royal Astronomical Society,2011,418(2):1258-1273.
[22] LENTATI L,SHANNON RM,COLES WA. From spin noise to systematics:stochastic process in the first international pulsar timing array data release[J]. Monthly Notices of the Royal Astronomical Society,2016,458(2):2161-2187.
[23] MATSAKIS DN,TAYLOR JH,EUBANKS TM. A statistic for describing pulsasr and clock stabilities[J].Astronomy and Astrophys,1997,326:924-928.
[24] BARNES JA,ANDREW RC,CUTLER LS, et al. Characterization of frequency stability[J].IEEE Transactions Instrumentations on Instrumentation Measurment,1971,IM-20(2):105-120.
Analysis of the effect of noises in pulsar timing on the stabilities of pulsar time
ZHANG Zhe-hao1,2,3, TONG Ming-lei1,2, ZHAO Cheng-shi1,2,ZHU Xing-zhi1,2, LIU Shu1,2,3, HAN Meng-na1,2,3
(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China;2. Key Laboratory of Time and Frequency Primary Standards, Chinese Academy of Sciences, Xi’an 710600, China;3. University of Chinese Academy of Sciences, Beijing 100049, China)
The existence of various kinds of noise in pulsar timing will give impacts on the stabilities of the established pulsar time in different levels. In this paper, based on the simulated data, we firstly give the impacts of the white noise and the red noise caused by the spin irregularities on the stabilities of pulsar time. It is found that the properties of the pulsar time scale stability affected by the red noise in timing are in accord with the theoretical anticipation. Meanwhile, we use the first data set released by the International Pulsar Timing Array to study how the stability of pulsar time is affected by the corrections of timing model parameters and noises. It is found that the influences from the corrections of timing model parameters and dispersion measure variations are much more significant than those from the white noise corrections. In addition, by the comparison to the simulated data, we verify that the noise in the real data set are still complicated after various corrections, and the power-law model cannot completely describe the red noises in the residuals.
pulsar timing; timing noise; pulsar time; stability
10.13875/j.issn.1674-0637.2020-03-0204-10
2020-01-17;
2020-04-09
国家自然科学基金资助项目(U1831130;U1531112);中国科学院青年创新促进会资助项目(2017450);国家自然科学基金面上资助项目(11873049)
张哲浩,男,硕士,主要从事脉冲星计时及其导航应用研究。

