高考新动向 巧用分析法

束峰琛

(江苏省新沂市第一中学 221400)

当已知条件与结论之间的联系不够明显、直接，或证明过程中所需用的知识不太明确、具体时，往往可以考虑采用分析法来处理，特别是一些含有根号、绝对值的等式或不等式等问题的证明时，常考虑用分析法，其思路是逆向思维，必须从结论出发，倒着分析，寻找结论成立的充分条件．结合近年的高考真题，分析法的应用往往出现在不等式、解析几何以及函数与导数的相关证明中，要加以重视．

一、不等式的证明

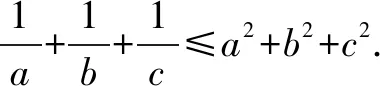
分析从待证的不等式不易发现证明的出发点，通过通分处理，结合条件加以变形，进而移项和配方，转化为平方和的关系式，分析其成立的充分条件即可证明相应的不等式成立．

证明因为a，b，c为正数，且满足abc=1，

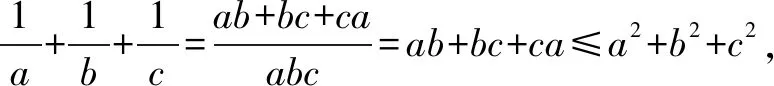
只需证a2+b2+c2-ab-bc-ca≥0，

即证(a-b)2+(b-c)2+(c-a)2≥0，

由于a，b，c为正数，而(a-b)2+(b-c)2+(c-a)2≥0显然成立，

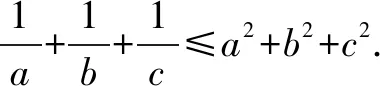
点评利用分析法证明不等式成立问题时，其分析的关键就是对所要证明的不等式加以等价转化，依据不等式的基本性质、已知的重要不等式等相关知识，综合通分、移项、配方等方法通过逻辑推理的基本理论来证明对应的不等式．

二、解析几何的证明

例2(2018年高考数学全国卷Ⅰ文科第20题(2))设抛物线C：y2=2x，点A(2，0)，B(-2，0)，过点A的直线l与C交于M，N两点．证明：∠ABM=∠ABN．

分析设出直线l的方程，与抛物线联立，转化为关于y的二次方程，结合根与系数的关系得到相应的关系式，利用平面几何方法进行分析法证明，根据∠ABM=∠ABN的等价条件Rt△BFN∽Rt△BEM的转化，利用相应边的比值的关系式的建立与转化，进行逆推分析，从而得以证明结论．

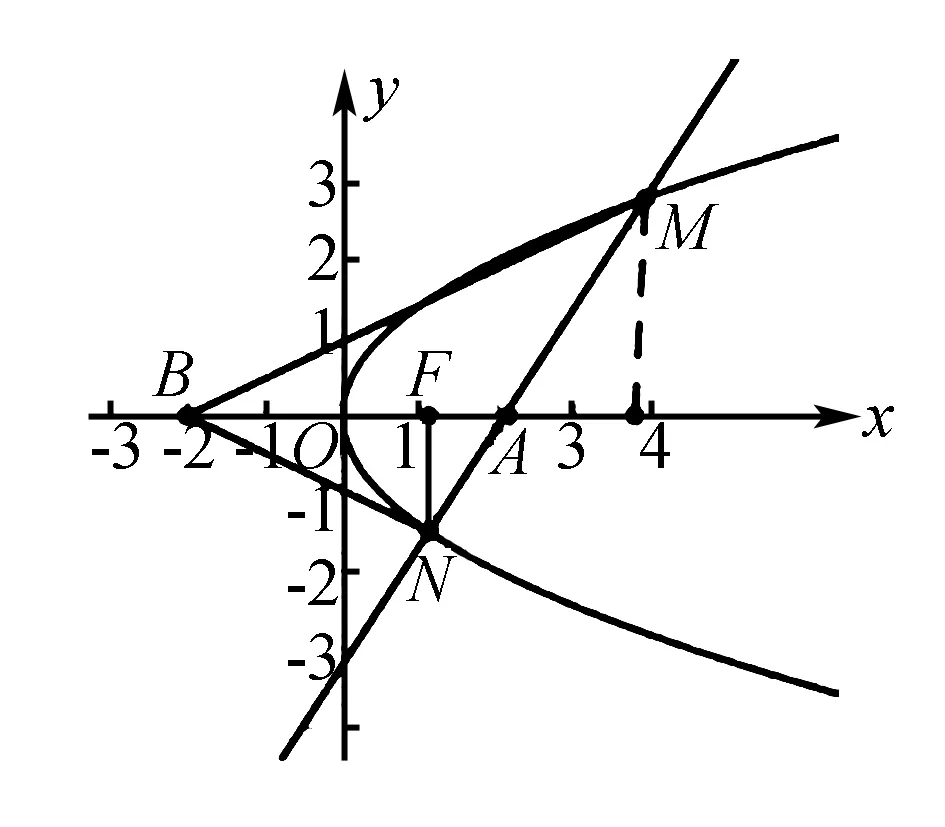
证明根据题意可设直线l：x=my+2(m∈R)，设M(x1，y1)，N(x2，y2)，不失一般性，设y1>0，y2<0，

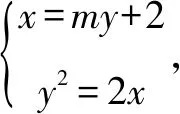
消去参数x并整理可得y2-2my-4=0，

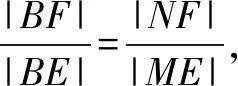
点评利用分析法证明解析几何中的相关问题，关键是转化为平面几何问题，抓住几何证明的脉络，利用平面几何的相关性质有条理地等价转化，同时又要充分融合解析几何的相关内容，从而达到转化与证明的目的．

三、函数与导数的证明

分析结合条件所要证明的不等式，通过分析法处理，分别借助ex≥ex的证明与应用，以及x-lnx-1≥0的证明来合理转化，从而得以分析法解决，巧妙证明．

构造g(x)=ex-ex，求导可得g′(x)=ex-e，则当01时，g′(x)>0，g(x)单调递增；

所以x=1是g(x)的最小值点，且最小值为g(1)=0，所以ex≥ex成立．

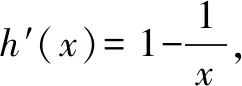
当x>1时，h′(x)>0，h(x)单调递增，

所以x=1是h(x)的最小值点，且最小值为h(1)=0，所以x-lnx-1≥0成立．

点评涉及函数与导数的相关证明问题，在近年的高考中经常出现，借助分析法的应用，可以有效抓住结论，利用结论的合理转化与条件的联系，有效串联，也是破解此类问题的思维过程中比较常见的证明方法．

分析法的实质是从要证明的结论出发，一步一步地推导，最后达到命题的已知条件(可明显成立的不等式(等式)、已知不等式(等式)、定义、定理或公理等)．应用分析法证明问题时要严格按分析法的语言表达，要有较强的逻辑推理能力，证明过程中必须有必要的文字说明，同时下一步是上一步的充分条件，其每一步的推导过程都必须可逆．