巧抓“隐圆” 妙解“最值”

李国林

(江苏省溧水高级中学 211200)

一、三角形中的隐圆

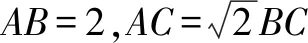
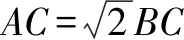
图1

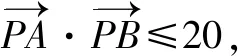
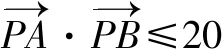
例3 在△ABC中，A,B,C所对的边分别为a,b,c，若a2+b2+2c2=8，则△ABC面积的最大值为____.

图2

分析类比上题的想法，也可以AB所在直线为x轴，AB中垂线为y轴

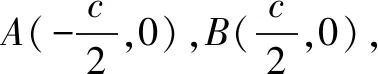
点评本题抓住所给条件是一个二次形式，以这样对称形式建系可得到较简单的“圆”的形式，回避了大量解三角形的运算，优化了解题过程，进而降低了本题难度.实际上，对于两个不同的定点A,B，若动点P满足PA2+PB2=AB2，对则点P的轨迹是以AB为直径的一个圆，类比这个结论，我们自然会想到：若PA2+PB2=m2(m>0)，则点P的轨迹是什么？点P的轨迹是一个圆，证明如下： 以AB所在直线为x轴，中垂线为y轴，建立平面直角坐标系xOy，不妨设AB=2a(a>0)，P(x,y)则A(-a,0)，B(a,0).

二、已经建立坐标系中的特殊条件

1.平面内有一定点，若一个动点到该定点的距离为常数，那么该动点的轨迹是“圆”

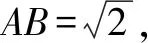
图3

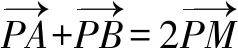
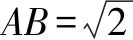
点评可以看到，从“形”入手，会使解题过程非常顺畅，该问题解决的关键点是挖掘动点M的轨迹是一个隐形圆.本题的关键是分析蕴含的几何条件，发掘其中的隐形圆，使问题的解决有了实质性的突破.

2.平面内有两个定点，若一动点到这两个两定点的连线彼此垂直，那么该动点的轨迹是“圆”

例5在平面直角坐标系xOy中，直线l1:kx-y+2=0与直线l2:x+ky-2=0相交于点P，则当实数k变化时，点P到直线l3:x-y-4=0的距离的最大值为____.

分析这是一道解析几何题，其常规思路是先联立直线l1,l2，进而求得交点P的坐标，再求P到直线l3最大值，运算繁冗.由于参量k不定，进而点P为动点，若能依据条件求得点P的轨迹，则问题转化为曲线上动点P到定直线的距离的最大值.

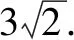
点评由于直线l1,l2处于运动状态，我们从动态中发掘出不动点A,B，这一策略的关键点是根据PA与PB的垂直关系挖掘出点P的轨迹是以AB为直径的隐形圆.

3.求动点的轨迹方程为隐含圆

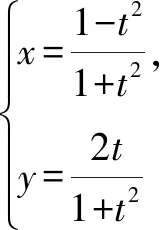
分析本题为参数方程与极坐标的结合，直线l化为普通方程后为定直线，点P的横纵坐标是有联系的，若能利用这个联系，就能简化运算了.

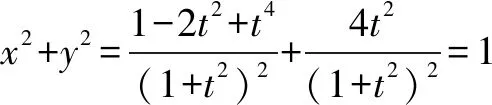
点评若从函数角度先表示距离，整个计算量较大，抓住点P横纵坐标的内在规律，考虑曲线C的轨迹，从“形”的角度来处理,让我们解题事半功倍.

总之，本文主要阐述隐含圆的发掘及其在解题中的作用.所述例题的特点都是题设条件涉及一个或多个动点，结论则需要求一条线段长度的范围或最值，从数的角度看，最终都要依靠函数、方程或不等式的知识来解决，且都有较大的运算量.这促使我们转换解题的视角和入口，将“数”的问题转化为“形”的问题，运用轨迹思想寻求动点的规律，从而发掘隐含圆，进而获得问题的最优解决方案.这需要我们学生能经常做一些积累，形成良好的知识网络.