工业机器人螺旋路径规划的研究与仿真

刘子贵

（江门职业技术学院,广东,529090)

0 引言

当钻井钻杆等螺纹有缺陷时，因报废成本较高，一般都会采用修复方式：先挖除缺陷，再对缺陷补焊，最后加工去除多余的补焊材料。如若碰到螺纹直径和螺距较大的情况，其在修复加工时无法采用常规的车削、铣削或镗削，而且成形刀具的制造极其困难。采用工业机器人补焊或加工螺纹，可以避免螺纹修复专用设备的投入，降低企业运作成本。因此，研究工业机器人的螺旋路径规划，具有十分重要的应用价值。

目前，针对直线、圆弧和规则曲线的路径规划已经非常成熟，但针对螺纹轨迹规划尚处于探索和实验阶段。首先必须建立螺旋线模型，然后需要选取数量合适的节点和刀具进给的步进角大小，最后工业机器人末端目标加工位置需要较为复杂的变换，才能确保机器人能够走出连续光滑的螺纹曲线，因此，这比传统工业机器人的连续路径规划更为困难。

1 建立机器人运动学模型

本文以YASKAWA六自由度串联机器人MH5F为研究对象，采用D-H建模法建立机器人坐标系，如图1所示。

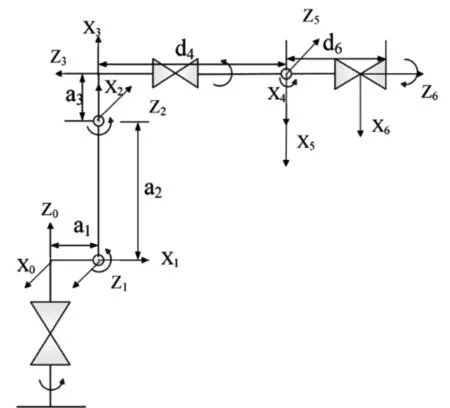
图1 MH5F机器人D-H坐标系

查询MH5F机器人的技术手册，可以确定图1中各关节连杆长度和连杆距离，a1=88mm，a2=310mm，a3=40mm，d4=305mm，d6=80mm。

MH5F工业机器人D-H 模型参数如表1所示。

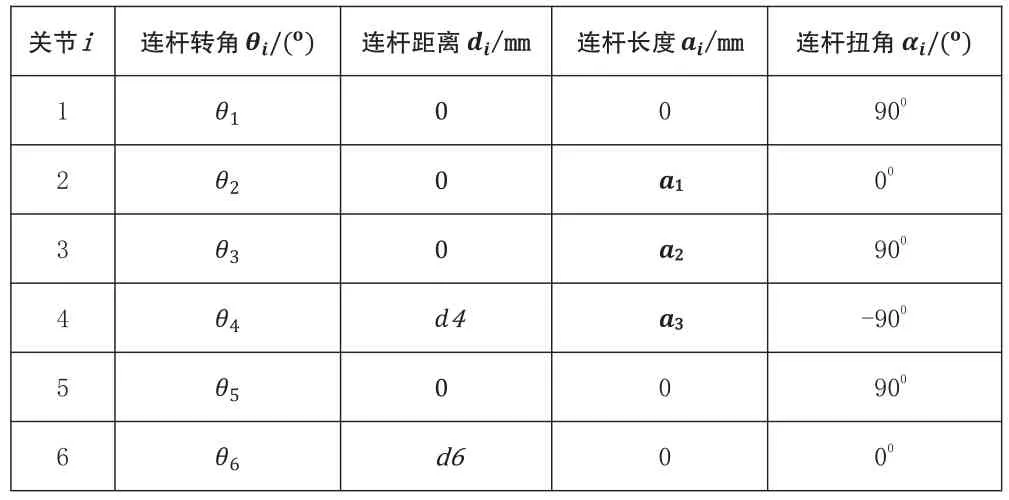
表1 安川MH5F工业机器人 D-H 模型参数

运用Robotics Toolbox 编制如下程序，建立机器人运动学模型，如图2所示。

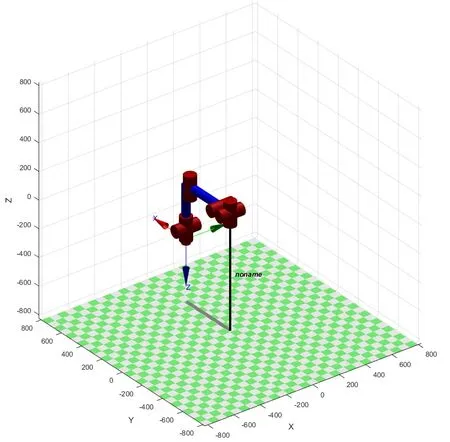
图2 MH5F机器人在MATLAB的模型

L1=Link('d',0,'a',0,'alpha',pi/2); %定义连杆1

L2=Link('d',0,'a',88,'alpha',0); %定义连杆2

L3=Link('d',0,'a',310,'alpha',pi/2); %定义连杆3

L4=Link('d',305,'a',40,'alpha',-pi/2); %定义连杆4

L5=Link('d',0,'a',0,'alpha',pi/2); %定义连杆5

L6=Link('d',80,'a',0,'alpha',0); %定义连杆6

robot=SerialLink([L1 L2 L3 L4 L5 L6]); %建立机器人模型

robot.display(); %显示机器人DH参数

theta=[pi/2 0 0 0 0 0]; %设定机器人初始关节角

robot.plot(theta)。 %显示机器人模型

2 螺旋线模型建立

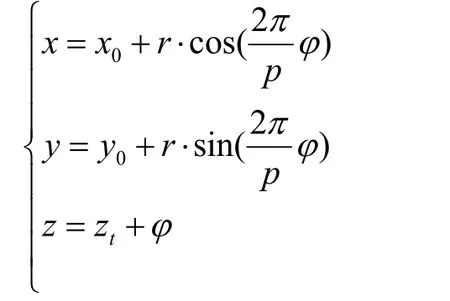
图3 螺旋线参数方程

根据传统的螺纹加工工艺原理，螺纹的加工精度受加工过程中加工刀具每次向前的步进角大小影响。因此，将空间螺旋线向平面坐标系投影，设步进角为，可获得半径为的扇形，如图4所示。

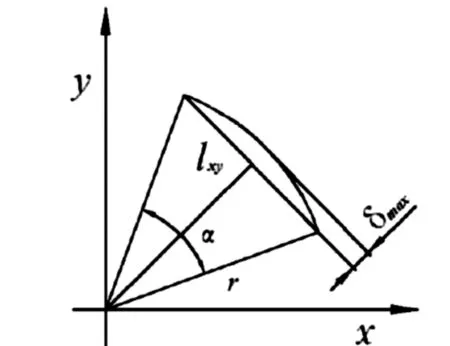
图4 螺旋线投影图

外螺纹有3种螺纹等级，分别为4h、6h和6g，假若取6h等级，查表得最大控制误差δmax为0.022mm。采用直线段拟合空间螺旋线，根据图4可推导出式（1），计算出误差δ，再经过变换得到步进角表达式，即式（2）。为了确保加工误差不超过δmax，必须让步进角≤0.0593。式（3）中的ceil为MATLAB函数，向正无穷取整，计算出n为106，n是一个螺距螺旋线上的节点数量。步进角越小，n越大，拟合精度就越高。

根据螺旋线参数方程、式（2）、式（3），利用MATLAB 编写下列程序，可生成5个螺距的空间螺旋线，如图5所示。

r=50; %螺纹半径为50mm

p=6; %螺距为6mm

alpha=2*acos(1-0.022/r); %根据控制误差，求得步进角

n=ceil(2*pi/alpha); %计算一个螺距的节点数量

x0=0; %初始坐标x的值

y0=0; %初始坐标y的值

z0=0; %初始坐标z的值

fi=0:p/n:5*p; %生成参数变量

x=x0+r*cos(2*pi/p*fi); %生成螺旋线x方向值

y=y0+r*sin(2*pi/p*fi); %生成螺旋线y方向值

z=z0+fi。 %生成螺旋线z方向值

plot3(x,y,z) %绘制空间螺旋线

图5 空间螺旋线

3 节点的截取与姿态

在螺旋线上选取若干个节点，工业机器人必须知晓这些节点的位置和姿态信息，然后分段执行，产生图5所示的空间螺旋线。

3.1 节点位置

根据式（2）、式（3）分割空间螺旋线的依据和原理，可以通过空间螺旋线的数学参数表达式计算节点的位置，运用MATLAB编写下列程序：

for i=1:5*n+1; %设置循环量

To(:,:,i)=transl(x(i),y(i),z(i)); % 生成齐次矩阵

end。 %循结束

即可得到5n+1个节点的位置齐次矩阵，也是机器人末端坐标原点在机器人坐标系中的位置，如下所示:

3.2 节点姿态

工业机器人末端要达到目标加工位置，一般需要经过三步变换：

1）工业机器人的末端坐标系先绕参考坐标系y轴旋转 -90。；

2）再绕z轴旋转180。；

3.3 节点位姿

由式(4)、式(5)可得机器人末端位姿，即：

利用MATLAB编写如下程序，求得各节点位姿，即T(:,:,i)，就是5n+1个节点位置和姿态的齐次矩阵序列。

Tp=trotz(pi)*troty(-pi/2); %绕y轴旋转-π/2,再绕z轴旋转π

fio=atan(p/(2*pi*r)); %求螺旋倾角

k=reshape([cos(fio*2*pi/p),sin(fio*2*pi/p),

zeros(1,5*n+1)],5*n+1,3); %生成螺旋轴

for i=1:5*n+1 %生成5n+1个节点

To(:,:,i)=transl(x(i),y(i),z(i)); %节点的位置

Tr(:,:,i)=angvec2tr(fi0,k(i,:))*Tp; %节点的姿态

RpY(:,:,i)=tr2rpy(Tr(:,:,i)); % 转化为roll、pitch、yaw角

T(:,:,i)=To(:,:,i)*Tr(:,:,i); %节点位姿

end。

4 螺旋路径仿真

运行上面的程序，可以获得各个节点的齐次坐标矩阵。利用逆运动学方程q(i)=ikine(T,'pinv')，求得每一个节点的关节变量值q。执行Robotics Toolbox中的驱动函数plot(q)，仿真出工业机器人的螺旋路径。程序如下：

q=ikine(T,'pinv'); %求每一个节点的关节变量值

robot.teach; %机器人驱动

hold on; %保持

plot3(x,y,z); %仿真螺旋线

robot.plot(q)。 %绘制螺旋线

5 结束语

本文通过Robotics Toolbox建立数学模型，获得螺旋曲线的节点位置和姿态以及螺旋线的导程等相关参数，令工业机器人具备了执行螺旋线路径功能，对扩宽其应用领域具有重要的应用价值。