《高等数学》中不定积分易错题分类剖析

左晓虹

(三门峡职业技术学院 公共教学部，河南 三门峡 472000)

1 将四则运算法则中的乘除运算法则用于不定积分

受中学数学代数运算的影响，部分学生忽视积分与代数运算的不同方式，将加减乘除四则运算直接套用到积分运算中。

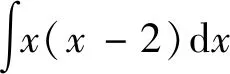
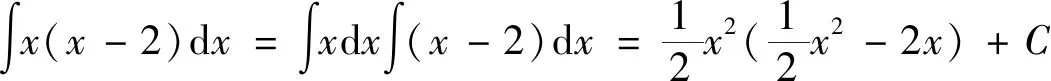
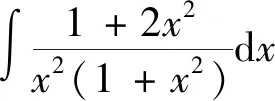
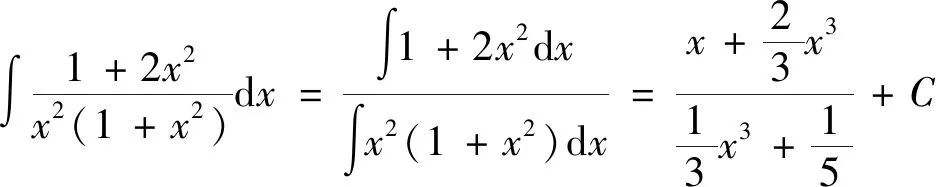
剖析：初学定积分的学生容易受极限四则运算法则及导数四则运算法则的影响，在解题过程中认为不定积分也具有加减乘除四则运算法则。错误的理解成如下计算公式：

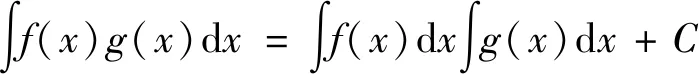
结论：不定积分有加减运算法则，但没有乘法运算法则，也没有除法运算法则。例1的正确解答是：

例2的正确解答是：

2 两类基本函数积分公式被混淆

幂函数和指数函数有相似的“外形”，部分学生在学习中混淆了二者的形式，也混淆了二者的原函数。

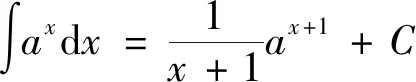
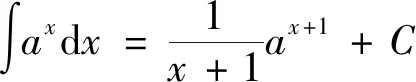
剖析：对于不定积分的基本公式，许多学生虽然能够熟记，但在运用过程中常常混淆两类公式。本题中出现的错误在于解题者混淆了幂函数和指数函数的积分公式，将指数函数的不定积分套用了幂函数的原函数。

结论：指数函数不定积分公式是：

幂函数不定积分公式是：

3 混淆积分变量

在积分的学习过程中，学生容易混淆积分变量和被积函数，尤其是当被积函数为两个及以上三角函数的乘积时，计算过程中学生稍一疏忽便可出错。

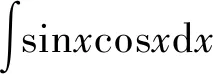
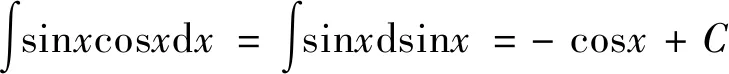
剖析：该题是一个复合函数的积分，积分的中间变量是sinx，发生的错误原因在于解题者盲目套用基本初等函数的不定积分公式，忽略了sinx其实质为中间变量，直接套用了正弦函数的不定积分公式进行解答。本题的正确解法为：

4 复合函数被错误地看成基本初等函数

凑微分法是积分的基本方法之一，在第一章节复合函数的教学中，教师要注意引导学生体会、感受符合函数的复合过程，即外函数、中间变量、自变量的“层层”包裹关系，通过对复合函数复合过程的练习，使学生明确复合函数是由六类基本初等函数经过有限次的复合运算而得到的函数，为导数和积分的学习打下基础。

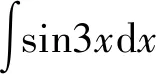
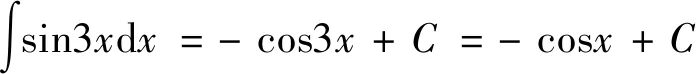
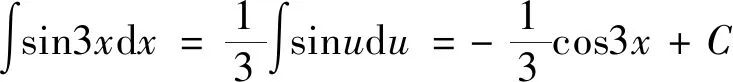
5 忽略了求出的不定积分成立区间

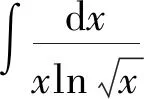
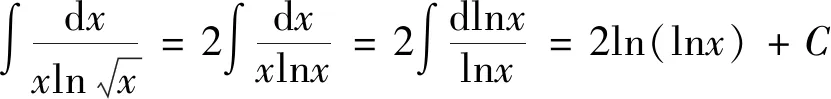
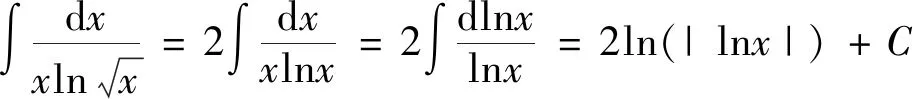
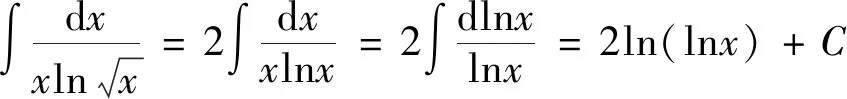
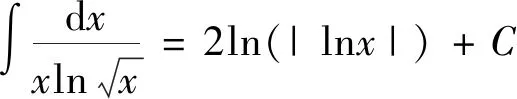
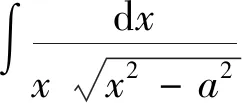
学生们在记忆或求解的过程中往往会错误地求解为：

剖析：没有注意被积函数中x与a的大小关系，如果分段讨论可有如下结果

如果不分段则可以通过如下式子表示

(1)

类似题的运算还有如下公式，注意公式(1)与公式(2)的区别

(2)

(3)

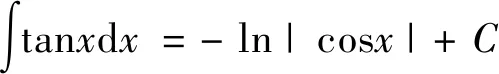
(4)

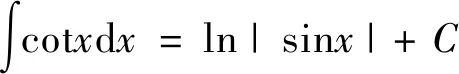
(5)

(6)

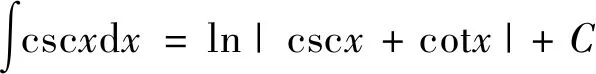
(7)

不定积分常见错误的求法还有很多，这里就不一一列举了。初学者要对比练习、勤于思考、善于总结、举一反三、学以致用，对所学知识做到融会贯通。