一种基于广义延拓逼近的动态滤波方法初步研究*

刘 成，李 芳，高为广，王 威

(1.北京跟踪与通信技术研究所，北京 100094；2.中国科学院国家天文台，北京 100101)

1 概 述

广义延拓逼近方法自1986年首次提出以来[1]展示了强大的生命力，应用横跨天文、力学、电磁学、机械、电子、通信和导航等多个领域，不断证明了其科学性和有效性。起初，广义延拓逼近方法的提出是为了解决大型天文望远镜设计中的实际问题，其后很快在一些光学与射电望远镜、雷达天线、弹性力学以及电磁场理论等领域得到实践，并被用于构造有限单元内的插值函数[2]。1991年，文[3]首次将广义延拓逼近方法引入太阳物理学，证明了延拓边界元空间的逼近性质和边界元近似解的收敛性，并于1993年出版[4]。2004年，文[5]重新对方法进行了系统归纳和整理。随后，广义延拓逼近方法开始受到科研工作者更加广泛的关注，并被推广至电子[6]、电力[7-8]、机械[9-12]、特种设备[13]、气象观测[14]等工程领域以及导弹制导等军事领域[15-16]。

同时，广义延拓逼近方法开始在导航与定位领域广泛应用。文[17]将其用于全球定位系统信号遮挡情况下，对伪距测量值进行外推，以维持用户基本定位能力，结果表明，可在15 s内维持优于5 m的伪距外推精度。文[18]对接收机钟漂进行建模以增强定位，结果表明，除维持遮挡情况下的定位外，还可提高正常信号情况下约24%的定位精度。文[19-24]先后开展了广义延拓逼近方法在导航卫星广播星历和精密星历插值中的应用，均表明精度优于一般插值方法。文[24]的研究表明，在选取合适参数时，广义延拓可达到毫米级的轨道插值精度，较拉格朗日(Lagrange)插值法高出56.6%～83.5%，较切比雪夫插值法高出20.9%～73.5%，且避免了传统插值方法的高阶振荡现象。文[25-27]研究了广义延拓逼近方法在卫星精密钟差中的插值应用，获得的绝大多数数据优于0.03 ns、全部数据优于0.1 ns的插值精度。文[28-29]利用广义延拓进行高程拟合，结果表明，精度优于传统二次多项式曲面法和多面函数法。文[30-33]将其用于导航信号的频率及载波跟踪，证明了广义延拓方法具有更优的信号跟踪性能。文[34-35]将其用于对载波测量值周跳的检测和修复，不同的研究结果均表明，广义延拓方法能够准确探测和修复1周以上的周跳。文[36-37]将其用于接收机码鉴相器中的码相位测量，结果表明广义延拓方法具有更高的精度和稳定性。文[38-41]探讨了广义延拓方法在卫星导航以及室内导航算法中的优化应用，进一步拓展了其应用场景。

上述诸多研究和应用均获得了理想效果，证明了广义延拓方法的科学性和正确性。然而，无论是轨道、钟差、高程还是伪距、载波、码相关峰，其特点都是一维、静态数据下的插值或外推计算，局限于广义延拓方法的一般形式。广义延拓方法能利用插值多项式实现对状态量的外推预测，然而，将其与滤波方法相结合，应用于动态数据处理领域，需要解决其测量修正问题并构建相应的误差模型，目前鲜有相关研究性工作。本文在上述研究工作的基础上对传统广义延拓方法进行了拓展，提出将其推广至动态滤波数据处理领域，研究和构造了基于广义延拓插值方程的滤波模型与框架，并推导给出了求解方法与流程。所提出的广义延拓逼近滤波方法既具备多维状态量的数据处理能力，也能满足状态量动态更新的要求，丰富了广义延拓方法的内涵。分别利用仿真数据和北斗卫星导航系统(BeiDouSatellite Navigation System, BDS)实测数据对方法进行了初步验证，结果表明，在高斯噪声、非高斯噪声以及实际导航应用环境下均获得了比卡尔曼滤波更好的性能，具有较大的发展潜力和应用价值。

2 广义延拓逼近数学方法

广义延拓逼近方法的数学本质是基于 “编结” 思想将数据集划分为多个相互连结的单元延拓域，并分段进行兼顾插值与拟合的数值处理，如图1，记某一单元延拓域Δe内的广义延拓二次插值函数U(t)为

图1 延拓域及其对应函数

U(t)=a0+a1t+a2t2,t∈[t1,t2]，

(1)

其中，ti为数据对应的时刻；a0,a1,a2为广义延拓多项式系数，可由延拓域中的数学模型确定：

(2)

也就是说，一方面要求广义延拓插值多项式在延拓域边界点上满足插值条件，保持边界点的数据特征和约束作用，并使得各段数据之间的变化具有更好的协调性。另一方面，利用分段插值区域的周围结点(包括内点)实现分段区域内外部数据的残差最小拟合，充分结合了插值和拟合方法的优点。

广义延拓逼近方法能根据实际情况，灵活构建具体的数学模型。例如，当对某个边界域节点的数值精度具有较高置信度时，可以将其增加作为插值约束点，以获得更准确的拟合结果；反之，可以放弃某个插值节点，将其退化为拟合点，降低对整体结果的影响，也可以采用三次或更高次的广义延拓多项式，以获得更高的数值处理精度。

3 基于广义延拓逼近的动态滤波方法

3.1 基本原理

基于广义延拓逼近的动态滤波方法的基本思想是利用广义延拓法构造一个具有一定先验数据长度、可灵活设置和优选插值约束点的移动窗口，对系统状态量进行高精度、具有抗差能力的逼近和预测，以取代传统卡尔曼滤波方法中的状态量时间更新(状态转移)过程，如图2。

与一般卡尔曼滤波方法相比，广义延拓逼近滤波方法使用了数据窗口，能够起到类似事后平滑的效果。卡尔曼滤波的数学本质是基于马尔科夫链的一步状态转移，利用最新历元n的状态量预测下一历元n+ 1的状态量。它的优点在于大幅减小了计算量，但同时也导致过于依赖当前历元状态量的精度；换言之，即使根据误差协方差矩阵P判断出当前历元n的状态量最优估计值具有很大误差，也只能继续利用该状态量估计值进行下一步预测。相比之下，广义延拓逼近滤波利用一个数据窗口进行预测，具有更好的平滑性和稳定性。

与一般的开窗滤波方法相比，广义延拓逼近滤波方法可以在数据窗口内灵活选择插值约束点，从而实现更好的抗差能力。例如，当当前历元n的定位误差较大时，可将其退化作为拟合点，以弱化其作用，并从窗口信息中另行选择更加精确的状态量估计值作为插值约束点(如图2)，从而在符合载体实际运动轨迹的同时，充分发挥可靠先验信息的约束作用，规避粗差影响，提高状态转移的精度和可靠性。

图2 广义延拓动态滤波原理示意图

3.2 插值约束方程的构造与状态量的时间转移

3.2.1 基本形式

若已知一段窗口长度为L的先验状态量最优估计值x^i(i=n-L+ 1,n-L+ 2, …,n)，通过将窗口范围内的某一历元j(j∈[n-L+ 1,n])的状态量最优估计值x^j作为插值点，其他历元的状态量最优估计值作为拟合点，可建立一个具有插值约束条件的广义延拓逼近方程：

(3)

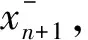
(4)

(5)

(6)

3.2.2 扩展形式

上节给出了广义延拓逼近方程的一般形式。实际上，方程也可采用更高阶的插值多项式形式：

(7)

或者可以进一步增加和采用某另一历元k(k∈[n-L+1,n]且k≠j)的状态量最优估计值，从而构成具有多个插值约束条件的方程形式：

(8)

以上扩展形式可根据具体需求灵活构造。

3.3 完整动态滤波框架

利用广义延拓逼近方法完成状态量的插值平滑更新后，结合测量更新处理步骤，即可建立完整的优化动态滤波框架模型，如图3。

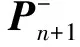
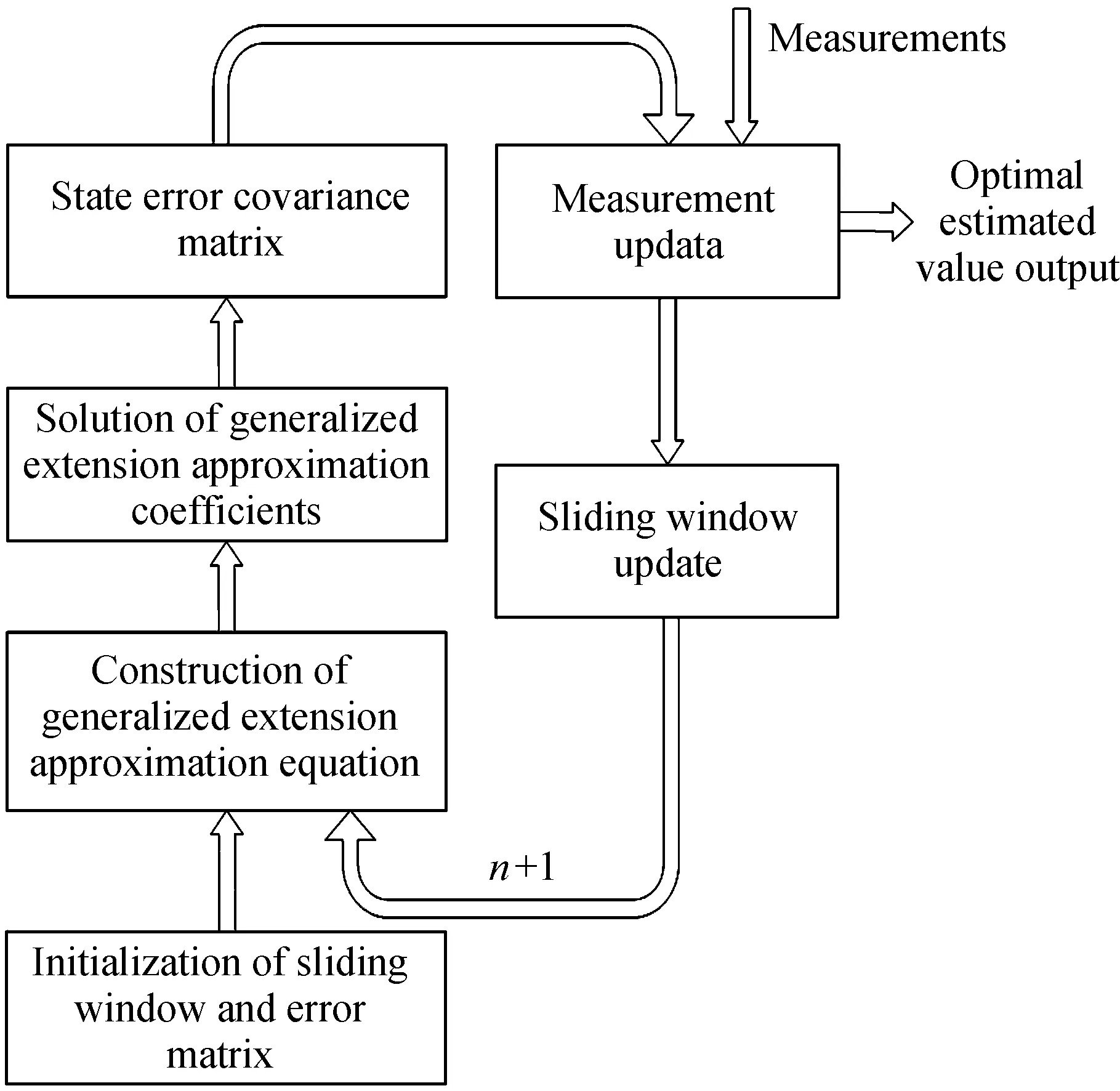
图3 广义延拓动态滤波模型

(9)

进行更新，其中，Q为系统转移过程噪声；A为系统状态转移矩阵。当广义延拓插值方程采用二次多项式时，对应状态量是匀速变化模型，有

(10)

其中，Δt为两时刻之间的时间间隔。当广义延拓插值方程采用三次多项式时，对应状态量是匀加速变化模型，有

(11)

在卡尔曼滤波测量更新过程中，分别计算n+ 1历元的权增益矩阵Kn+1、状态量最优估计值X^n+1及其协方差矩阵Pn+1：

(12)

其中，C为测量关系矩阵；R为测量噪声协方差矩阵。

4 求解方法与步骤

对广义延拓动态滤波逼近方程的求解，可采用线性化展开的形式。具体地，将(3)式中的插值约束方程改写为

(13)

将(13)式代入最小二乘公式可得

(14)

(15)

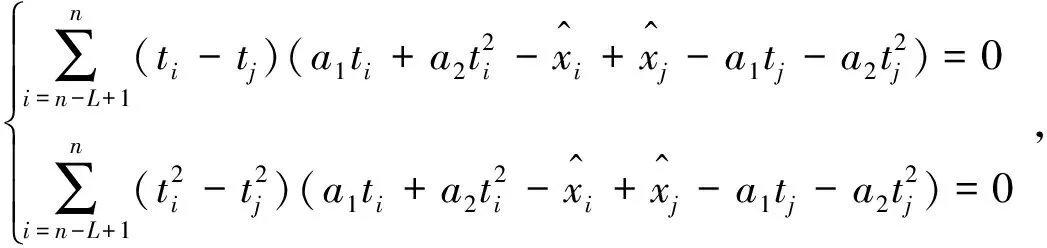
(16)

(17)

(18)

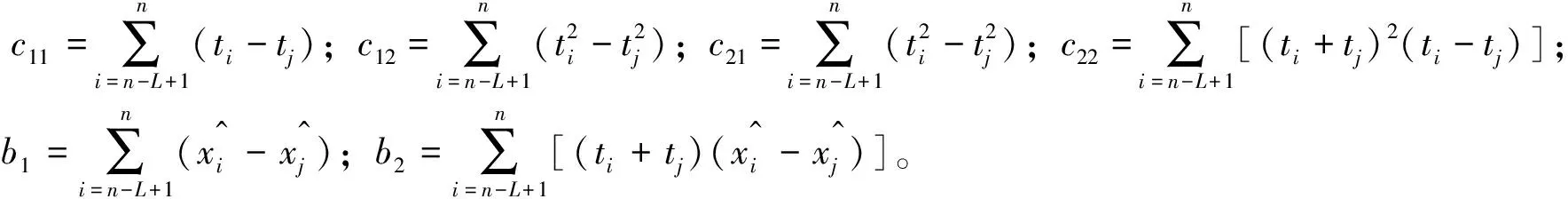
(19)

5 仿真计算

5.1 信号去噪处理仿真

分别对正弦信号在白噪声和有色噪声情况下的滤波性能进行仿真。仿真时间T=0～30 s，步长Δt=0.1 s，重复计算1 000次。利用蒙特卡洛模拟对精度结果进行统计，通过与广泛应用的卡尔曼滤波器进行比较，对广义延拓逼近滤波的性能进行分析和评估。

5.1.1 白噪声滤波性能

首先，加入满足r～N(0, 0.1)分布的高斯白噪声进行数值仿真，考察和分析滤波方法的基本特性。两种滤波器的初始状态量为X0=[0 0]，初始协方差为P0=diag([0.1 2])，初始过程噪声Q0=[0.0 0.000 5; 0.000 5 0.01]，初始测量噪声为R0=0.01，广义延拓逼近滤波的窗口长度L=20，插值约束点为当前历元观测点。两种滤波方法的效果如图4，误差概率统计如图5。其中，卡尔曼滤波的均方根误差约0.083，广义延拓逼近滤波的均方根误差约0.069，提升约17%。

图4 白噪声下的滤波仿真结果

图5 白噪声下的滤波误差概率统计

5.1.2 有色噪声滤波性能

在上述高斯白噪声基础上，加入有色噪声e(k)=0.2(x(k)+0.9x(k-1))，滤波器误差参数和窗口数据长度均保持不变。广义延拓逼近方法和卡尔曼滤波方法均基于噪声高斯分布的理想假设，但在实际应用中，理想高斯分布的情况很难真实存在，因此，考察两种方法在有色噪声影响下的性能具有实际意义。两种滤波方法的效果如图6，误差概率统计如图7。其中，卡尔曼滤波的均方根误差约0.113，广义延拓逼近滤波的均方根误差约0.102，提升约10%。

图6 叠加有色噪声后的滤波仿真结果

图7 叠加有色噪声后的滤波误差概率统计

5.2 卫星导航实测数据处理验证

2020年1月，采用自主研制的全球导航卫星系统(Global Navigation Satellite System, GNSS)多模导航接收机在北京地区测量得到的北斗卫星导航系统观测数据(包括伪距、多普勒、载波和广播星历)对方法进行实测验证，并与卡尔曼滤波器以及经典希格(Sage)开窗滤波器处理结果进行比较。几种方法的定位输出结果如图8，其中，广义延拓逼近滤波的窗口长度取L=15。

从图8可以看出，广义延拓滤波方法有能力获得比经典卡尔曼滤波和希格开窗滤波更优的性能，具有应用潜力。以实时动态(Real-time Kinemaic, RTK)载波定位解算结果作为基准，统计3种方法的东西向平面误差，结果见表1。

表1 滤波定位误差结果对比

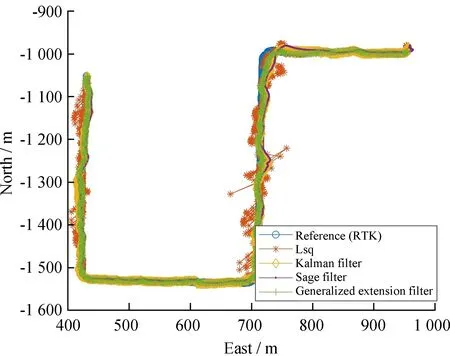
图8 北斗导航滤波定位结果对比

6 结 论

本文在广义延拓逼近理论的基础上，提出了一种动态滤波更新方法。研究和构造了基于广义延拓插值方程的滤波模型与框架，并推导给出了其求解方法与流程。方法既具备多维状态量的处理能力，也能够满足高低阶状态量动态更新的要求。在一段移动平滑窗口内构造和求解广义延拓插值多项式，实现对系统状态量的时间转移，具有更好的平滑效果，拓展了经典广义延拓数学方法的内涵。与一般开窗滤波方法相比，广义延拓逼近滤波方法数据窗口内插值点的位置及数量均可灵活选取，从而可通过锁定最新观测点或最准确的先验观测点，实现更高的精度和抗差能力。分别利用正弦信号数值仿真和北斗卫星导航实测数据对方法进行了验证，结果表明，在高斯噪声和非高斯噪声仿真下均获得了比卡尔曼滤波更优的性能，验证了将广义延拓逼近理论与滤波方法相结合的可行性。另外需要指出的是，目前初步构造广义延拓滤波模型仍是基于卡尔曼滤波误差假设条件的近似，相信随着后续理论和模型的完善，方法将具备更优的性能与更大的应用价值。