基于虚拟天文馆对全天相机姿态的精确测量*

李小波，刘 煜，崔辰州，宋腾飞，王晶星，樊建康

(1.中国科学院云南天文台，云南 昆明 650216；2.中国科学院国家天文台，北京 100101)

全天相机是利用朝向天顶的鱼眼镜头获取全天空图像的照相机。全天相机已获得广泛应用，主要在以下领域：(1)地基遥感全天空云量自动化监测[1-2]。在数字图像处理软件中，利用经验或理论确定的阈值判别云或蓝天，然后对云进行分类和计量。大多数算法[3]是基于瑞利散射或饱和度对从三原色计算出的某指标进行判断[4-6]。其他计量云量的方法有比较天空辐射亮度、比较两个或多个窄波段的辐射值、比较白昼实测和虚拟天空[7]、比较夜间实测和虚拟星场、神经网络[8]、超像素分割[9]等。对薄云、临近太阳的天区、特殊天气情况、夜间云量、临近地平线的云量的判断仍是难点，对云高和云状的自动监测仪器仍需进一步实验研究；(2)监测天文址点的夜天光和云量[10-11]。在我国天文界, 全天云量相机已应用于丽江天文观测站[12]、青海观测站[13]、西部天文选址[14-15]等；(3)用于监测流星的全天相机网络[16]；(4)对舰船进行天文导航定位[17-18]。在以上各方面的应用中，均需要准确掌握像场的参数。较高的标准是准确获得物-像的投影关系，能够将图像中的特征点还原为天球上的坐标，这对于监测和定位航空器、流星等小尺度物体至关重要。较低的标准是掌握图像中的实际方向和天顶位置，以确定特征物的方位。对于任何用途的全天相机图像，至少要知道其东南西北方向。

理想情况下，全天相机的光轴指向天顶，视场中心与天顶重合，图像的纵轴与测者子午线重合。但是，实际的全天相机不能达到这个标准。首先，相机一般安置于高山、沙漠、建筑物顶部等，由于条件所限，施工时无法像安装大型天文观测设备那样对方位进行准确的校准，难免产生不能忽略的安装偏差；其次,全天相机大多无人值守，恶劣天气、野生动物等外力有可能使相机偏离初始安装姿态；再次，对相机的维修、改造、清洁等作业也会改变其姿态。所以，在处理全天相机图像时，需要依据参照物对图像进行矫正，获得其旋转角、天顶位置等基本参数。不仅需要对新安装的相机初光获得的图像进行精细测量，在日常运行中也要不定期再次测量并更新参数，这样才能生成可靠的可视化产品，为监测工作提供有效的服务。另外，准确测量像场也是矫正镜头畸变，进行坐标变换，进而实现较高标准的基础。

恒星是全天相机视场中最可靠的参照物，而虚拟天文馆大大简化了对星表的检索和计算工作，在图形化界面中可以快速完成检索恒星和测量坐标的操作，适用于测量全天相机姿态。同时，虚拟天文馆具有直观的用户界面，往往可以离线工作，对计算机配置要求相对较低，相比于虚拟天文台[19-21]，更符合野外观测站的实际条件。

基于上述需求和条件，本文拟达到4方面的目标：(1)开发一套基于虚拟天文馆的像场测量方法，通过比较特征恒星的地平坐标及其像点在像平面上的极坐标，高精度测量相机的姿态，并探索在自动化、可移植化等方面深入开发该方法。(2)基于一台典型全天相机的监测数据，通过像场测量其姿态，确定图像中天顶的位置及其与像场中心的距离，达到亚像素的精度; 测量测者子午线的方位；测量相机像场的基本几何参数。(3)在重大维护前后分别测量上述参量，了解维护工作对相机姿态的影响。(4)矫正姿态偏差并生成符合规范的可视化产品。

1 研究资料

本文使用的全天相机安放于四川稻城县的无名山二号观测点。无名山是中国科学院云南天文台选址与日冕观测团组在西部天文选址科考工作中发掘的优秀天文址点[15,22-24]。该相机由光学、采集、控制和保护系统组成，其中，光学系统基于一枚适马(Sigma)牌焦距4.5 mm、光圈2.8的鱼眼镜头，视野略大于180°；采集系统基于一台佳能(Canon)牌EOS-60D单镜头反光相机; 控制软件和数据库安装于一台研祥牌工业控制计算机，根据日月的高度、月相、天光亮度调整感光度和曝光时间；光学和采集系统封装于一个能抵御恶劣天气的机箱中，镜头通过透明半球罩指向天顶，形成圆形的像场(图1)。图2展示了位于机柜顶部的天窗的基本结构，该半球罩半径为10 cm，镜头前端高出半球球心5 cm，视野达到地平线以下。在半球罩的周围安装了用于除霜露的电热装置。自2015年11月初光以来，该设备对无名山的天空进行了连续稳定的监测，观测人员对半球罩进行例行清洁，技术人员不定期对相机进行检修、更换零件、升级部件等操作。

图1 无名山全天相机于2017年6月5日日初时拍摄的一帧图像

图2 (a)无名山二号点全天相机的设计图；(b)实际外观

Stellarium[25](1)http://stellarium.org/是由Cháreau等人开发的一种开源虚拟天象模拟软件，基本星表包含60多万颗恒星，附加星表包含177多万颗恒星，可还原大气层的光影效果，并叠加赤道式和地平式坐标网格，满足本文的需要。基于无名山二号观测点的位置(纬度：29°6′24.59″，经度：100°6′32.07″)、海拔(4 800 m)以及指定的时间，即可获得该时该地的星图，并查找某恒星的地平坐标值等参数。图3显示了其用户界面，在左上角列出了选定恒星(HIP 746)的详细参数，包括在指定观测条件下的地平坐标。为了便于显示和打印，已经对星图做了色调反转处理，下同。

图3 Stellarium虚拟天文馆的用户界面

分析无名山全天相机于2016年10月和2017年6月获得的4组全天彩色图像，其中，夜间两组共两帧，均在良好的气象条件下拍摄，用于分析星场；昼夜数据两组共11帧，用于测量像场。数据的基本参数列于表1。2017年5月底对相机的安装位置和伺服系统进行调整，像场发生了变化。因此，使用这两个月的数据比较维护前后的相机姿态。

表1 本研究使用的全天相机监测数据

2 测量像场的几何参数

全天相机指向天顶拍摄，获得近似等角投影的全天空半球像，天空物点的纬度和方位角对应像点的极距和极角。在像场的边缘，部分天际线被山峦、监测设备等遮挡。采用标记边缘点的方法测量圆形像场的中心、半径等几何参数。

2.1 选取监测数据

无名山全天相机于2016年10月5日和2017年6月5日进行了连续的监测，使用两种时间和空间分辨率分别采集了285和352帧图片。经观察，在晴天太阳或满月升起/落下的时刻，入射光线的天顶角约为90°，视场边缘的山峦和镜头的边框均被照亮，太阳光也没有直射镜头而产生炫光，像场边缘较为明亮，而像场外基本黑暗，便于对视场边缘进行定位，如图1。选取两组共计11帧图片，分别编号为D1-d和D3-d。

2.2 测量方法和结果

将像场的边缘点进行椭圆拟合，得到其长短轴、中心坐标、偏心率等几何参数，并计算它们在每组图像中的均值。在后续计算中基于这些参数对图像进行分析。在图1中，白色椭圆是拟合的像场边缘。

D1-d和D3-d数据的测量结果列于表2。长半轴和短半轴的差异仅为半轴的2‰，像场可近似为圆形，所测长、短半轴长度的均值即为圆半径。

表2 全天相机像场的实测几何参数

在D1-d和D3-d的观测日期之间，曾对全天相机进行了深入维护。若以图片y方向的分辨率为单位对半径、中心x、y坐标分别进行归一化处理，可得D1-d和D3-d的上述3个量的归一化数值分别为(0.428 9,0.759 0,0.504 8)和(0.429 5,0.761 1,0.504 4)，两者的差异分别为(0.14%,0.28%,-0.07%)。由此可知，常规维护对像场基本几何参数的改变是微小的，在云量分析中可以忽略。

3 测量天顶位置

3.1 测量原理

鱼眼镜头成像最显著的光学畸变是圆形像场中的桶形像差。假设鱼眼镜头的桶形像差是轴对称的，并忽略像场中心与天顶的偏差，那么，投影中桶形像差只对像点的极距有非线性影响，并不改变极角，任意两个恒星像点对天顶投影点形成的张角不受桶形像差的影响，与天球上的实际张角相同。依据这个原理，首先选取若干颗恒星，在图像上测量其坐标，同时，使用虚拟天文馆得到其地平经纬度；然后在天顶区域构建一个网格，逐格点计算各恒星像点对格点形成的张角，并与虚拟值比较，当实测张角与虚拟张角最为接近，即两者的差异在网格局部区域的二阶曲率为正时，可判定该格点对应着天顶。

在选取恒星时，应当遵循3个原则：(1)低星等，该全天相机使用商业CCD而不是星敏感器，只对低星等恒星才能准确响应；(2)孤立，相比于天文望远镜，全天相机的像元分辨率相当低，定位精度约为4′，不能有效区分星团、双星或数密度大的天区，挑选孤立、与背景有较高反差的恒星，便于识别；(3)中等纬度，高地平纬度的恒星与天顶的角距离较近，在计算极角时对测量误差较为敏感，而低地平纬度恒星光程较长且成像受镜头像差影响较大，两者均不宜选作实验的样本。

基于上述分析，使用小(～10)、中(～50)、大(～200)3个容量的恒星样本，分别测量天顶位置。

3.2 选取恒星样本

2016年10月20日无名山气象条件较为理想，全天相机工作正常，获得了时序稳定、图像清晰的时间序列。在日落(18:39(2)北京时间，下同)与月亮升起(22:41)之间(3)时间序列中日月消光的时刻，不是日月到达绝对地平的时刻，天空中没有强光源干扰，各天区的星空较为清晰，满足本文的需要。经挑选，采用于21:21:00获取的图片(图4(a))作为样本，记为D2-n(表1)。

图4 (a)样本D2-n, 2016年10月20日21:21:00全天相机获取的夜间图像；(b)旋转后的实测星图

按照前文所述的原则，选取9颗恒星，它们的地平纬度在30°～60°，地平经度分布较为分散，记为样本S2-9。采用二维高斯拟合测量其坐标，以下称为实测星场。图5中，在局部放大的反转图像上，方片标记了样本像点的位置。同时，在Stellarium虚拟天象软件中，获得恒星样本在D2-n拍照参数下的地平坐标值，以下称为虚拟星场。表3列出了样本S2-9在图像正交坐标系中的实测坐标、HIP(Hipparcos星表[26])编号及其地平经纬度。图6在地平坐标中绘制了样本的位置。中心十字为天顶; 箭头标记正北方向; 刻度标记地平纬度，单位为度。

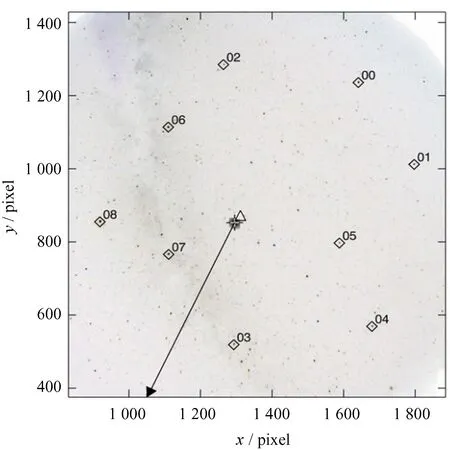
图5 恒星样本S2-9像点的分布，用方片标记

图6 在地平坐标系中绘制的恒星样本S2-9(星号)的分布

表3 恒星样本S2-9的实测和虚拟参数

3.3 计算天顶位置

从时间序列中初步确定天顶位于HIP 109056和HIP 107975的中点附近。在虚拟和实测星场中分别测量这两颗恒星的坐标，记于表3的末两行。以它们的中点为中心选取一个边长约为4°的方形区域，记为天顶候选区域Z，在图5中用箭头原点处的灰色矩形标记。

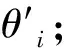
(1)

图7绘制了某次计算中网格内δ(x,y)的坑状分布，x和y轴的坐标单位为0.02像素，纵轴的单位为度。δ(x,y)的二阶曲率为正，说明天顶确实在Z中，该坑的最低点具有最小的δ(x,y)值，它就是图像的天顶位置。

图7 天顶区域Z网格内δ(x, y)的坑状分布

考虑到在对δ(x,y)的数值计算中，各恒星的排序会影响计算结果，一方面是因为张角对中心点位置的敏感度与张角的大小成正比，另一方面是因为对恒星像点的测量有角分级(像素尺度)的误差。为了减小某特定排序中的随机误差，将多次计算结果的重心作为天顶。在图8的计算结果中，共进行了1 024次计算，每次使用随机函数对样本S2-9中的恒星进行排序，共得到1 024个天顶候选位置，它们分布在一个4 × 4像素的矩形区域内，候选天顶的平均δ(x,y)为0.39°。该图的中央方片表示散点的重心，格点间距为0.02像素，坐标单位为像素。去除1.5倍标准差以外的离群值并取平均后，得到天顶位置(1294.87, 853.50)。使用不同的网格密度、离群值剔除标准、计算次数对样本S2-9进行了多次计算，所得天顶坐标只有亚像素级的差异，如表4。在图5中，小十字表示从天顶候选区域Z(灰色方块)中遴选出来的天顶；三角号表示全天相机圆形像场的中心；背景是图像D2-n的相应区域；坐标单位为像素。

图8 使用样本S2-9计算所得的候选天顶点

3.4 使用较大容量样本的计算结果

在D2-n星图上另选取了一个含有204颗恒星的样本S2-204，重新计算天顶坐标，结果列于表4。在使用不同参数的多次计算中，散点均形成了聚合的团簇，综合所得天顶坐标仍然只有亚像素级的差异，但是天顶在x，y方向与S2-9的计算结果有约3像素的位移。此差异是由样本造成的，对恒星像点位置测量的随机误差在高纬度天区得到放大，进而影响到天顶的定位，与计算参数的设置无关。因为这两个恒星样本的容量有数量级的差异，所以认为S2-204的结果更可靠。在表4第10行的计算中，选用了较小的格点间距和离群值剔除标准，采用天顶坐标为(1 298.03 ± 0.34,856.60 ± 0.38)。以图像y方向的长度为单位，归一化天顶坐标为(0.751 18 ± 0.000 20,0.495 72 ± 0.000 22)。

3.5 相机的竖直姿态偏差

测量相机的光轴与天顶的偏差，是本文要解决的重要实际问题。首先使用Z区域的HIP 109056和HIP 107975作为参考点，依据两者星点的角距离和像点的距离，求得相机在天顶区域的平均空间分辨率为0.114 5°/像素。由此可得，图像的天顶位置(1 298.03, 856.60)与像场中心(1 311.48, 872.22)的角距离为2.36°。

针对2017年5月底相机姿态调整的情况，使用D3-n星图另采集了一个含有40颗恒星的样本S3-40，代表性结果见表4第11行。天顶位置与像场中心的角距离达7.64°，该次维护作业明显加大了竖直姿态的偏差。

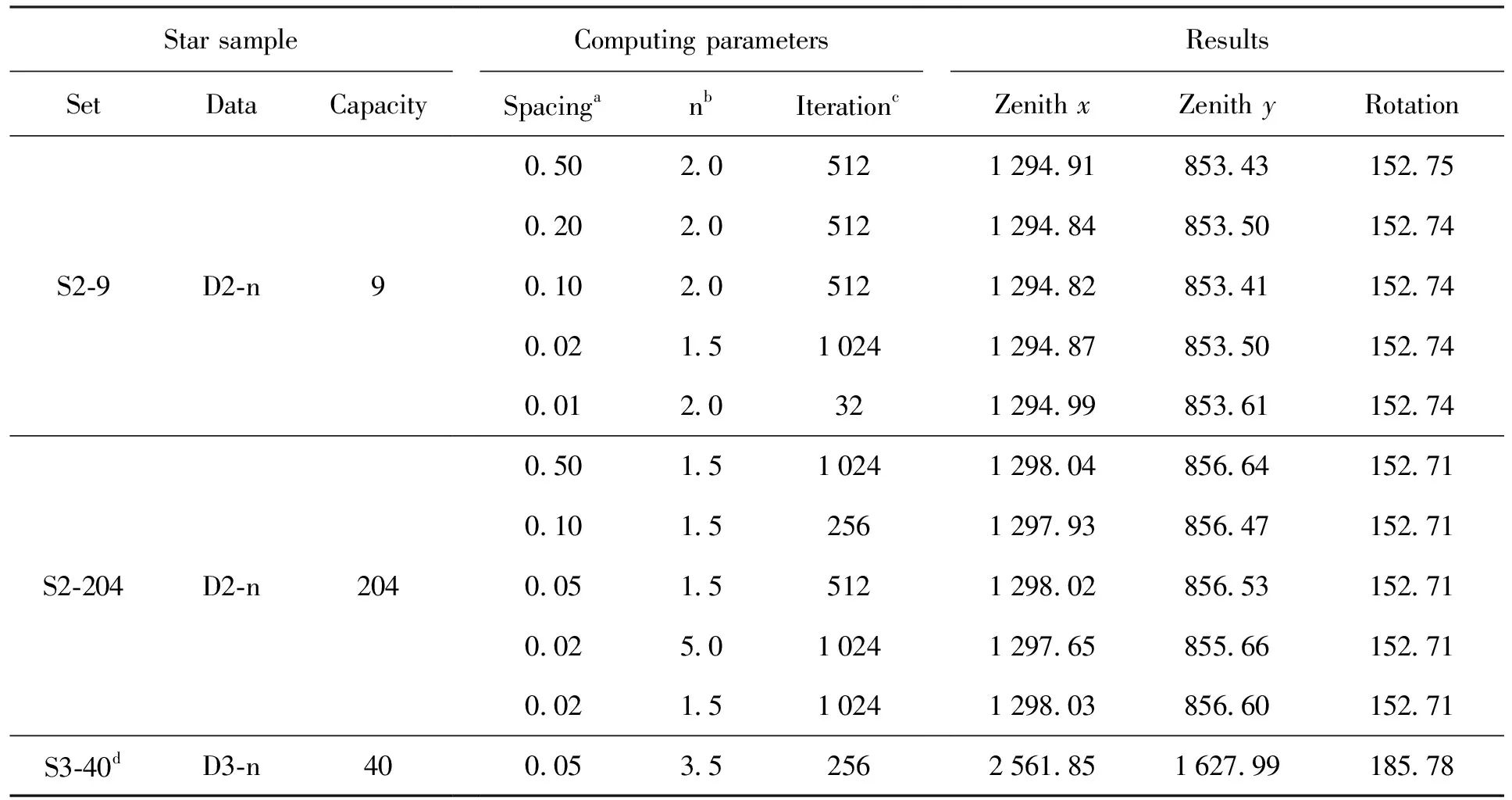
表4 天顶和旋转角的计算结果

4 测量旋转角

全天相机的旋转角ψ，即图像纵轴与测者子午线正北方向的夹角，可以根据恒星样本方位角的虚拟值和实测值的差值求得。

ψ=mean({φi-φi′}),0≤i≤N，

(2)

其中，φi和φi′分别为在实测星场和虚拟星场中恒星i的方位角。S2-9和S2-204的旋转角分别为152.74 ± 2.55°和152.71 ± 1.58°。图9绘制了S2-204的{φi-φi′}。图5和图6中的实线箭头分别表示实测与虚拟星图的正北方向，箭头与y轴的夹角是图像的旋转角。将原始图像旋转ψ后，两者重合。图4(a)和(b)分别是旋转前后的样本D2-n。小十字标记天顶，坐标单位为像素。在图4(b)中，图像纵轴为正北方向，这样就制成了符合行业规范的图片和动画。

图9 用样本S2-204计算图像D2-n的旋转角

在对S3-40样本的计算结果中(表4)，旋转角为185.78°，与D2-n的测量结果有较大差异。在近年的使用中，每次开箱维护都会改变旋转角，因此，在每次维护之后都应重新测量旋转角并反馈给数据处理程序。

5 结论与讨论

5.1 结 论

使用无名山全天相机于2016年10月和2017年6月获得的4组全天图像，采集了容量分别为9、40、204的恒星样本，从虚拟天文馆获得了恒星的地平坐标，通过像场对姿态参数进行了精确的测量。主要结果为：(1)开发了一种基于虚拟天文馆计算恒星坐标功能的测量方法，使姿态测量建立在容量较大的参考恒星上，为全天相机图像的深入分析处理奠定了基础。特别是采用网格法对天顶的定位达到了亚像素的精度，有望满足陨星和航空器等高定位精度监测的需求。该方法对相机的视场、像差、可见天空角面积等参数没有依赖性，具有较强的可移植性。(2)提高相机姿态精度的首要任务是减小光轴的天顶角，而维护作业可能会造成光轴与天顶有不可忽略的偏差。按2016年10月20日全天相机的姿态，像场的天顶坐标为(0.751 18 ± 0.000 20，0.495 72 ± 0.000 22)，与像场中心的夹角为2.36°；而在2017年6月5日的数据中，两者的夹角达到7.6°。(3)常规维护作业对像场几何参数的改变甚微(≤0.28%)，在一般图像分析中可以忽略。无名山全天相机的像场呈正圆形，以图像y方向的长度为单位，其半径和中心坐标分别为0.428 9和(0.759 0，0.504 8)。(4)测量了图像的旋转角并在可视化产品中按制图惯例进行了旋转。每次维护相机都可能改变旋转角，并需要重新测量。

5.2 讨 论

本测量的主要误差来源是：(1)单帧图像中恒星像点的定位误差。夜间长时间曝光(～30 s)和视宁度的时空不均匀性等均可造成偶然误差；(2)光学系统的桶形像差。由于光轴倾斜，光学投影的径向非线性被传导到切向，在测量结果中形成了系统误差。在下一步的工作中，可以采用升级硬件以缩短曝光时间、综合多帧测量结果、改进测星方法等手段抑制偶然误差。通过测量镜头径向畸变参数，在预处理中将图像矫正为等角投影，以抑制系统误差。

影响全天相机像场的首要姿态偏差是其光轴与天顶的夹角。如果光轴不竖直，不仅对视场和投影的轴对称性会造成系统性的影响，而且每次在维护后需要重新测量姿态。如果在设计和施工中大幅度提高竖直方向的姿态精度和稳定性，在野外使用中光轴的天顶角始终符合监测任务的精度要求，只需要测量新的旋转角即可。

在天文观测中，一个潜在的误差来源是观测设备的时钟误差。由于天球旋转的速度是360°/d即15″/s，时钟误差0.1 s就会造成角秒级的定位误差。但是，对于无名山全天相机而言，按照天顶区域0.057 2°的像元分辨率(5 184 × 3 456)，时钟误差达到13.7 s才能造成像素级的定位误差。无名山全天相机使用互联网时钟对工控机内置时钟进行校准，其精度完全可以满足恒星定位的需要。

天文导航技术的发展为研究的进一步深入提供了很多可借鉴的方法。本研究与天文导航的研究具有一定的异同。一方面，天文导航的测量目的是定位，要求准实时性；而本研究的测量目标是地基设备的姿态，对时效性要求不高，但期望在类似设备中具有较强的可移植性。另一方面，二者都主要解决实测星场的获得、矫正和比较计算。全天相机充足的恒星样本容量提高了结果的可靠性，并为深入分析提供了可能。如果在后续研究中需要采集大容量的恒星样本，可以从天文导航的研究中借鉴成熟的从星图中批量获取和比较恒星坐标的方法[27-28]，并开发(4)Stellarium软件执行的是GNU General Public License，用户可以修改程序从虚拟天文馆中自动输出坐标矩阵的接口软件。在后续研究中有针对性地改进数据压缩方法，开展对全天相机光学系统的分析和矫正，并提高对数据格式、图像瑕疵和气象条件的适应能力，以期把本研究移植到类似设备。

致谢：无名山观测站在次仁汪堆、洛绒次称、宋其武等同志的辛苦劳作下得以稳定运行，在此深表谢忱。