基于响应曲面法的氟塑料两相流泵优化设计

张德胜，梅剑，赵睿杰，黄俊，金永鑫

(江苏大学国家水泵及系统工程技术研究中心， 江苏 镇江212013)

氟塑料离心泵由于其具有强耐腐蚀性特点，被广泛应用于化工、制药、冶金、电力等行业中，用于输送强酸、强碱、强氧化剂、有机溶剂等强腐蚀性介质，是耐腐蚀介质循环系统中关键的动力设备.但是，大型氟塑料两相流离心泵受介质黏度和颗粒的影响，效率非常低.此外，叶轮部件由氟塑料制成，因此其耐磨性能差.许多学者研究了离心泵叶轮的几何结构及其参数以及含有固体颗粒的两相流动对泵性能的影响[1-3]，但对氟塑料离心泵的耐磨损性能研究鲜有文献报道.

离心泵叶轮的优化常通过试验设计方法得到数据样本，采用响应面模型、克里金模型、人工神经网络模型等构建优化目标与设计参数之间的近似函数关系，借助Isight，COMSOL等平台，通过优化算法对近似函数关系进行寻优求解，以获得最优控制参数组合.相较于上述模型，响应面模型可将体系的响应作为一个或多个因素的函数，运用图形技术将这种函数关系显示出来，直观地判别优化区域.张勇等[4]采用响应面法，以同向出流水力旋器为研究对象,以结构参数为输入变量,以底流口含油浓度为响应目标，分析旋流器分离效率随各结构参数在一定范围内的变化情况.代翠等[5]根据叶轮几何参数对噪声影响的显著性筛选出关键参数后，通过响应面模型构建关键参数与噪声、水力效率指标之间的回归模型.

近年来，随着CFD技术的快速发展，数值模拟方法因其成本低、限制条件少，且能够准确地反映泵内部流动情况，已被广泛应用于流体机械的优化设计，并对指定工况下的泵的扬程、效率等性能参数进行较准确的预测[6-7].文中以氟塑料离心泵叶轮为研究对象，搭建基于Matlab的泵性能数值模拟优化平台，针对氟塑料离心泵效率及叶轮磨损问题，应用CFD技术，基于DPM模型[8-9]对叶轮在不同外形参数下进行液固两相流模拟，对叶轮的叶片包角φ，叶轮进口直径D1，叶片进口安放角β1，叶片出口角β2，叶轮出口直径D2，叶片出口宽度b2等6个参数采用Box-Behnken Design[10]设计54组参数组合，通过响应曲面法分析各参数间的交互作用对泵效率及磨损情况的影响，得到优化后的叶轮的几何参数组合，提升氟塑料两相流离心泵的综合性能.

1 离心泵内固液两相流场定常计算

1.1 泵模型及其参数

选取SJB400-250-300型氟塑料离心泵为研究对象，该泵的设计性能参数分别为流量Q=1 200 m3/h，扬程H=40 m，转速n=1 450 r/min；叶轮的主要几何参数分别为叶轮进口直径D1=300 mm，叶轮出口直径D2=432 mm，叶片数Z=5，叶轮出口宽度b2=73 mm，叶片进口安放角β1=25°，叶片出口安放角β2=22°，叶片包角φ=100°，蜗壳基圆直径D3= 450 mm.

模型泵实物如图1所示.图2为泵内各水体域结构.

图1 SJB400-250-300型氟塑料离心泵Fig.1 Fluoroplastic centrifugal pump of model SJB400-250-300

图2 水体域结构Fig.2 Fluid domain structure

1.2 网格划分及无关性验证

采用Pro/E软件对离心泵的进出口段、叶轮、前腔、后腔及蜗壳进行三维造型，为使湍流在管内得到充分发展，将进出口段延长至管径的6倍.应用ICEM软件对离心泵的各水体区域进行非结构网格划分.为确定合适的网格数，对计算域进行了5组网格划分以验证网格无关性，如图3所示.

由图3可以看出，当网格总数为5 098 909时，扬程、效率趋于稳定.此时，进口段、前腔、叶轮、后腔、蜗壳及出口段的网格数分别695 067，420 483，1 513 102，1 694 538，448 857，326 862.

1.3 磨损模型

采用Fluent中的DPM(discrete phase model)模型对模型泵进行定常数值计算.叶轮壁面处由于颗粒的冲蚀效应造成的磨损是关于颗粒冲击、颗粒及壁面属性的复杂函数，可认为冲蚀是粒子冲击角及速度之间的函数[11]，即

(1)

(2)

式中：E为磨损速率；k为与材料有关的系数；Vp为颗粒冲击速度；f(γ)为冲击角的函数，其中冲击角为颗粒轨迹与壁面的夹角；指数n通常取1.3～2.5，对氟塑料材质，取n=1.95[12-13].

定义氟塑料离心泵叶轮的磨损率为

(3)

式中：Er为磨损率；mp为单个粒子的质量；C(dp) 为颗粒直径函数；b(υ)为颗粒相对速度的函数；A为叶轮的磨损面积.

1.4 控制方程和边界条件

液相为连续相，是不可压缩流体，其控制方程为连续方程与动量方程[14].固相为离散相，泥沙颗粒的运动速度可分解为雷诺时均速度与脉动速度，采用牛顿第二定律计算时均速度，颗粒扩散随机模型计算脉动速度.

颗粒运动方程为

(4)

式中：xp为固体颗粒的坐标；up为颗粒的雷诺时均速度，与水流时均速度一样；u′p为颗粒脉动速度.

时均速度up的变化满足

(5)

式中：FD为拖曳力；Fp为压强梯度力；FA为附加质量力；FH为Basset力；FL为Saffman升力；FG为质量力；FC为Magnus力.

由于流场中离散相的颗粒浓度较小，连续相的流体速度较大，并且连续相和离散相之间具有较大的密度差.因此，固体颗粒受到的压强梯度力、附加质量力、Basset力、Saffman力和Magnus力等不予考虑，时均速度up的变化可简化为

(6)

(7)

式中：CD为拖曳力系数；ρf为水流密度；dp为泥沙颗粒的直径；ρp为泥沙密度；uf为颗粒位置处水相的时均速度.

数值计算选用可实现的k-ε湍流模型求解N-S方程.设定进出口边界条件分别为速度进口和自由出流，为减小进出口对计算域的影响，适当延伸进出口长度.对液固两相流的计算,采用DPM模型进行求解，压强项选择Standard，固壁满足无滑移条件，收敛残差设为1.0×10-4.

1.5 试验验证

为验证数值模拟方法的正确性，在江苏亚梅开式试验台上对原型泵进行固液两相的外特性试验.两相介质物性参数分别为水，常温，密度为997 kg/m3,黏度为0.89 mPa·s；沙，密度为2 500 kg/m3；进口处颗粒相体积分数为10%.

不同流量工况下原型泵试验结果与数值计算结果对比如图4所示.由图4可以看出，数值计算结果与试验数据比较吻合，在1 320 m3/h流量工况下效率与扬程的数值计算值与试验值的相对误差最大，分别为2.47%和3.32%，这表明该数值计算方法是可靠的，即可通过数值模拟对该泵的性能进行预测.

图4 数值计算与试验结果对比Fig.4 Comparison between computational and experimental performances

2 优化设计方法

2.1 优化目标

以氟塑料离心泵的效率η和磨损率Er为优化目标，其水力性能目标优化的数学模型为

求X=[φ,D1,β1,D2,b2,β2]T，使

F(X)=[f1(x),f2(x)]T→max，

(8)

式中：F(X)=[f1(x),f2(x)]T是二维向量，分别对应效率η和磨损率Er.

2.2 试验方案

响应曲面法是利用合理的试验设计方法得到试验数据，采用多元二次回归方程拟合因素与响应值之间的函数关系，对回归方程的分析求解最优工艺参数，解决多变量问题的一种统计方法.各变量变化范围由泵的装配尺寸进行限制，其中叶片包角φ=101°～121°，叶轮进口直径D1=290～306 mm，叶片进口安放角β1=22°～42°，叶轮出口直径D2=421～441 mm，叶片出口宽度b2=68～76 mm，叶片出口安放角β2=20°～40°.

在响应曲面法中，常采用CCD(中心组合设计)及BBD(Box-Behnken)2种试验设计法，CCD虽然比BBD试验能更好地拟合曲面，但是在本例中，CCD设计出的一些点超出了原定的水平，不容易达到，且相较于CCD，因素数相同时BBD设计所需试验次数少，可节约大量计算资源，因此选用BBD试验设计法.根据Box-Behnken Design设计方法得到54组叶轮的几何参数组合及计算结果如表1所示.

表1 试验方案Tab.1 Test case

2.3 响应面分析

基于计算结果数据，针对各优化目标建立多元回归方程.经计算得到效率η和磨损率Er回归方程的回归系数R2分别为0.986，0.975，表明采用响应曲面法对泵性能进行优化是可行的.

以效率η为优化目标，额定工况下，响应面模型如图5所示.

图5 η与各因素的交互作用Fig.5 Interaction between η and other parameters

图5a表现了以效率η为目标时，D1和φ之间的交互性影响：D1和φ均为高水平以及D1和φ均为低水平时，扬程达到最大值；D1取高水平时，效率η随φ值增加而增大；D1取低水平时，效率η随φ值增加而减小.

图5b表现了D2与β1的交互性关系：额定工况下，D2不变，随β1的增大效率也随之提高；β1一定，随D2的减小效率值呈上升趋势；当D2达到最小值，而β1达到最大值时，效率最高.

图5c表现了β2与b2的交互性关系：在β2为20°时，效率随b2增加而减小；β2为40°时，b2的变化对效率影响不大；在b2为68 mm时，β2对效率几乎没有影响；b2为76 mm时，效率随β2减小而下降；当β2与b2均取最大值时或最小值时，效率明显高于其他区域，且效率较高的点分布于β2取40°，b2取76 mm与β2取20°，b2取68 mm的对角线附近.

以磨损率Er为优化目标，额定工况下，响应面模型如图6所示.

图6 Er与各因素的交互作用Fig.6 Interaction between Er and other factors

图6a表现了以磨损率为优化目标时，D1和φ之间的交互性影响：D1取高水平时，磨损率变化趋势总体为随φ值增大而减小；D1取低水平时，磨损率随φ的增大而将增大；φ一定时，随D1的增大，磨损率先增大后减小；较低的磨损率主要出现在高水平及低水平的D1附近.

图6b表现了D2与β1的交互性关系：额定工况下，D2不变，随β1的增大，磨损率总体呈下降趋势；β1取低水平时，随D2的减小磨损率随之减小；随着β1的增大，D2对磨损率的影响逐渐减小；磨损率较小的点分布于D2取441 mm，β1取42°与D2取421 mm，β1取22°的对角线附近.

图6c表现了β2与b2的交互性关系：在β2为20°时，b2的变化对磨损率影响最大，磨损率随b2增加而增大，在b2为76 mm时，磨损率达到最大值；磨损率较小的点分布于β2取40°，b2取76 mm与β2取20°，b2取68 mm的对角线附近.

以效率η和磨损率Er为优化目标，拟合得到的响应面模型的数学表达式为

η=62.41-0.3φ+0.048D1+0.9β1-0.13D2-0.3b2+0.44β2+1.64φD1+0.96φβ1-0.48φD2+1.13φb2-0.13φβ2+0.13D1β1+0.23D1D2+0.1D1b2-1.17D1β2-0.048β1D2-2.15β1b2-0.074β1β2+0.24D2b2-1.47D2β2+0.84b2β2+0.7φ2+0.68D12-0.16β12-0.055D22-0.46b22-0.075β22,

(9)

106Er=0.41+0.016φ-0.017D1-0.031β1+0.037D2+0.021b2-0.016β2-0.005 6φD1-0.003 7φβ1+0.000 643φD2-0.001 9φb2-0.001 1φβ2+0.005 5D1β1-0.000 45D1D2-0.003 2D1b2+0.003 7D1β2-

0.003 7β1D2+0.001 9β1b2-0.012β1β2-

0.000 82 93D2b2+0.004 2D2β2-0.007b2β2+

0.000 45φ2-0.000 7D12+0.003 2β12+0.000 38D22+

0.004 2b22-0.782 5β22.

(10)

2.4 离心泵性能多目标优化

离心泵的多目标优化问题数学描述如下：

(11)

式中：F(X)=[f1(x),f2(x)]T是二维向量，即目标函数F(X)中有2个分目标函数f1(x),f2(x)，

(12)

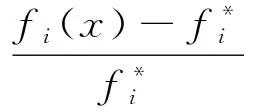
根据优化得到的上述6个参数值，重新建模，并对其进行CFD数值计算.

3 结果与分析

通过Matlab统一多目标函数并求解得到最优叶轮模型，经Fluent计算得到效率及磨损率，相较于原模型，扬程达到42.14 m，满足设计工况下的扬程要求，效率提升了8.98%，磨损率下降了6.64%(原模型扬程为39.58 m，效率为66.88%，磨损率为1.407 2×10-6kg/(s·m2)).优化后设计参数与原模型设计参数对比如表2所示.

表2 设计参数对比Tab.2 Comparison between original and optimi-zed cases

图7为模型泵优化前后效率与磨损量曲线对比，可以看出，在流量为720～1 200 m3/h时，效率增长率呈上升趋势，并在靠近1 200 m3/h工况处达到最大，随后因泵内颗粒流动速度加快，加速过流部件的磨损，导致泵性能下降，效率增长率的下降速率加快.因磨损率与泵性能呈负相关性，为便于分析，纵坐标取磨损率的倒数，即为Er-1.在含沙水条件下，优化后1/Er值均明显高于原模型，即过流部件的磨损情况得到明显改善，证明本优化结果是成功的.

图7 优化模型与原始模型性能对比Fig.7 Comparison of characteristics between optimi-zed and original pumps

4 结 论

基于响应曲面法，针对氟塑料两相流泵叶轮各主要参数对泵效率及磨损率的影响进行了研究，得到如下结论：

1) 基于响应曲面法得到的泵性能参数的数学模型，计算结果与试验结果相近，因此，基于响应曲面法的氟塑料两相流泵优化设计方法是可靠的.

2) 优化后，各流量工况下效率得到显著提升，叶轮磨损率显著下降，额定工况下的优化模型效率为72.88%，磨损率为1.407 2×10-6kg/(s·mm2)，相较于原模型，效率提升了8.98%，磨损率下降了6.64%.

3) 曲面响应法能够真实反映离心泵叶轮各设计变量与优化目标间的复杂的非线性关系及交互性影响，为离心泵的水力性能的提升和磨损量的控制提供了直观、高效可靠的优化分析方法.