基于模拟退火算法的五缸往复泵曲柄相位布置方案优化
高金鹏,姚春东,柳青扬,刘天明,焦会明
(燕山大学机械工程学院,河北 秦皇岛066004)
往复泵是一种高效节能的流体输送机械,广泛应用于石油、轻工、食品及农业灌溉等行业[1].曲轴是往复泵传动系统中的核心部件,其可靠性对泵整机的工作性能及寿命有较大影响[2].不同曲柄相位布置方案下,任一液缸对应曲柄初始相位不同,其对应曲柄销所受连杆力大小不同,使得曲柄销所受转矩及曲轴危险截面所受弯矩也不同.由于曲轴主要承受周期性的交变载荷作用,使其易产生疲劳破坏,降低了往复泵可靠性及工作性能.为改善曲轴结构受力,提高其强度,故对曲轴曲柄相位布置方案进行优化设计,具有实际的工程意义.
目前有关曲轴曲柄相位布置的研究相对较少,郭卫等[3]通过对乳化液泵两支承五拐曲轴挠力载荷分析,以曲柄相位为设计变量,曲轴运行周期内最大惯性力矩最小为目标函数,对曲柄空间分布位置进行优化设计.闫志琴[4]通过对曲轴曲柄2种不同布局下曲轴的受力分析,认为曲轴所受合力会因曲柄相对位置的变化而改变.贾品元[5]提出往复泵设计者在设计时应尽可能通过选择合理曲柄内错角配置改善曲轴结构受力.MAGGI等[6]通过对压缩机曲轴的曲柄排列布置优化,减小了曲轴的应力水平.文献[7-8]以往复泵吸入管各截面间流量波动、断流时间和曲轴受力最优为目标,对七拐两支承曲轴曲柄初相角布置方案进行了优化,并以曲轴强度为目标对五拐两支承曲轴曲柄初相角进行了优化.虽有针对往复泵五拐两支承曲轴曲柄相位布置方案的研究,但是随着曲轴支承数目的增加,目前属于超静定结构的五拐六支承曲轴已发展为主流趋势,有必要进一步对五拐六支撑曲轴曲柄相位布置方案进行优化.
文中提出一种可用于往复泵曲柄相位布置方案优化的新方法,即以曲柄初始相位角为设计变量,以曲轴危险截面所受最大弯矩最小为目标函数,结合适用于求解组合优化问题全局最优解的模拟退火算法对曲柄相位布置方案进行优化,为往复泵在工农业领域应用中的设计提供参考.
1 曲柄相位布置方案优化模型
1.1 理论基础
目前成熟五缸往复泵产品动力端多采用一级双斜齿轮机构进行减速,曲轴受力分析如图1所示.

图1 曲轴受力分析Fig.1 Force analysis of crankshaft
由于曲轴受力较复杂,为便于计算,作如下假设[9]:
1) 吸入过程中,十字头及活塞(柱塞)组件所受缸内压力远小于排出过程中受力,故不考虑吸入过程中缸内压力.
2) 不考虑泵阀滞后角对吸入、排出过程中缸内压力的影响.
3) 将各运动部件间的相互作用力视为集中力,其几何中心视为支反力作用点.
4) 由于各运动部件间摩擦力、自身重力及惯性力相对活塞力、连杆力较小,故忽略不计.
五缸往复泵各缸内曲柄滑块机构运动规律相同,故文中任选第i号缸对应曲柄滑块机构进行分析,曲柄滑块机构的运动与受力简图如图2所示.
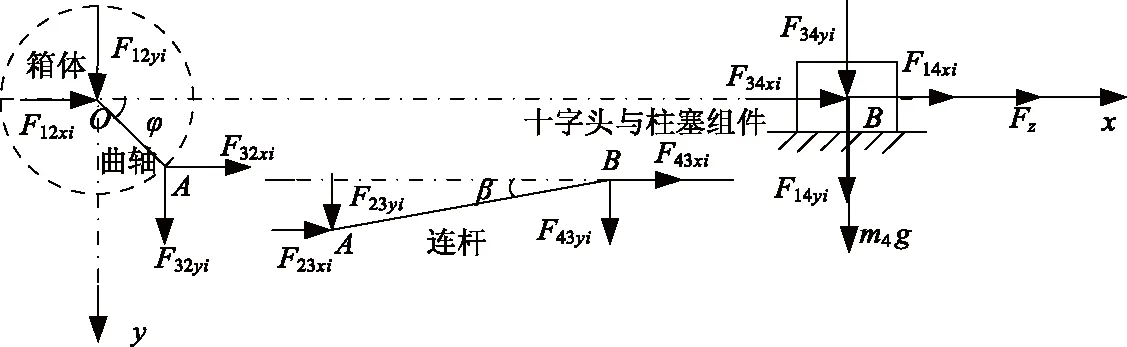
图2 曲柄滑块机构运动及受力简图Fig.2 Sketch of movement and force in crank-crosshead mechanism
令连杆比λ=r/l,则做往复运动的活塞(柱塞)与十字头组件的运动方程[9]为
(1)
(2)
αi=-rω2(cosφi+λcos2φi),
(3)
式中:φi为曲柄旋转角度,φi=ωt+ψi;ψi为初始相位.
在连杆的任意位置,有
(4)
则
βi=sin-1(λsinφi),
(5)
式中:βi为连杆与活塞(柱塞)运动方向间夹角.
活塞(柱塞)力为
(6)
式中:p为缸内介质压力;d为活塞(柱塞)直径.
连杆力及沿坐标x,y轴方向分力为
(7)
Flx=Flcosβi=Fz,
(8)
(9)
曲柄销所受转矩为
Ti=rFlsin(φi+βi)=
(10)
齿轮机构分布在曲轴两侧,五缸往复泵曲轴的偏心力呈对称分布且相互抵消[10-11],轴承的支反力与过曲轴轴心的离心力对齿轮啮合力的大小无影响,故齿轮机构的啮合力只取决于作用在曲轴上的连杆力,曲轴与齿轮机构所受作用力示意图如图3所示.
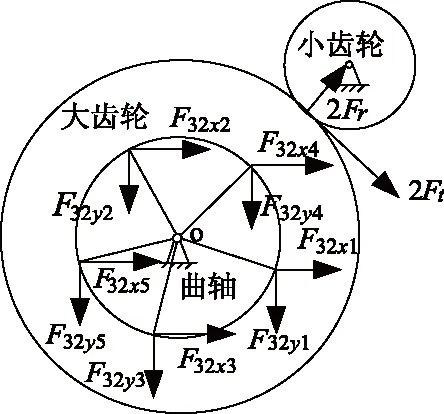
图3 连杆力与齿轮啮合力示意图Fig.3 Diagram of connecting rod forces and meshing forces of gear
斜齿轮切向力[11]为
(11)
式中:r2为大齿轮分度圆半径.
斜齿轮的径向力与轴向力[11]分别为
(12)
斜齿轮在曲轴两端呈对称分布,由对称关系即可得出右端大齿轮所受切向力与径向力分别为
Ft1=Ft2,Fr1=Fr2.
(13)
五缸往复泵曲轴结构为五拐六支承,属于超静定结构,文中采用“分布均摊法”求解系统超静定问题.为求解曲轴各轴承座支反力,进行如下假设:
1) 假设各液力端作用在各曲柄销上的力互不影响,仅对相邻两箱体支座产生作用力.
2) 端部齿轮受力只对相邻箱体支承座产生作用力.
3) 箱体支承座受力为均摊各力的矢量叠加.
将五缸往复泵曲柄连杆机构及曲轴组件所对应的两端斜齿轮机构分为中间5部分和两端部分,对曲轴齿轮组件各部分分别按“悬臂梁”与“简支梁”求解相邻支承座受力,然后通过矢量求和求出曲轴各支承座所受支反力Nxk及Nyk.曲轴端部支承1受力分析如图4所示,由式(14)求得曲轴端部支承1、支承6的支反力Nxk,Nyk.
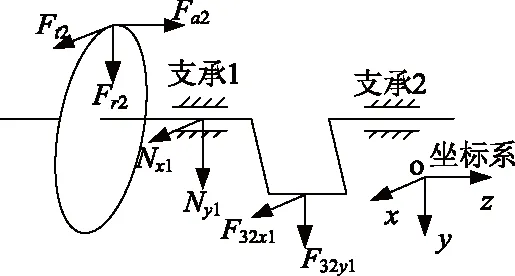
图4 曲轴端部支承1受力分析示意图Fig.4 Diagram of force analysis on support 1 of crankshaft
(14)
式中:k为支承序号,k=1,6;i为液缸号,k=1时i=1,k=6时i=5;mkg为相应齿轮端部重力.
曲轴中部支承2受力分析如图5所示,由式(15)求得支承2—5处所受作用反力Nx2,Ny2.
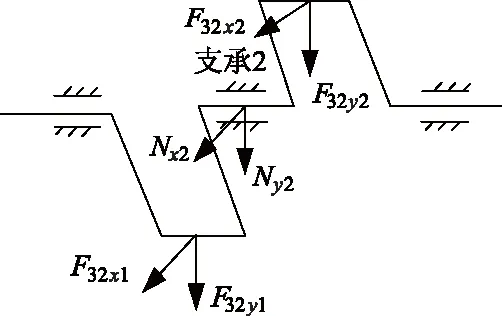
图5 曲轴中部支承2受力分析示意图Fig.5 Diagram of force analysis on middle support 2 of crankshaft
(15)
式中:k为支承序号,k=2,3,4,5;i为往复泵缸号,i=k.
为确定所选曲轴各个危险截面的弯矩、转矩,并为强度校核提供依据,需对曲轴截面内力进行计算.基于曲轴几何结构与受力情况,文中曲轴各计算危险截面的选取如图6所示.

图6 曲轴危险截面Fig.6 Crankshaft critical sections
选择以上截面的理由[12]如下:
1) 曲轴所受主要应力是由连杆力所引起的弯曲应力,故选取曲柄销与曲柄截面突变处为危险截面.
2) 曲轴两端装配大斜齿轮的台肩处截面积较小,故也应选取为危险截面位置.
根据以上分析,可计算曲轴各危险截面的弯矩Mx,My及所受总转矩T,如危险截面E处:
(16)
同理可求得其他危险截面处受力.
扭转与弯曲的组合变形是机械工程中常见的情况,考虑到曲轴材料为塑性材料,根据曲轴危险截面j处所受转矩及合弯矩,按第四强度理论条件,计算危险截面j的弯扭组合应力,计算公式[13]为
(17)
式中:Wj为曲轴危险截面j处抗弯截面系数.
1.2 设计变量
五缸单作用往复泵曲轴各曲柄对应的相位角有0°,72°,144°,216°和288°.各曲柄相位角在同一相位布置方案中只能出现1次,任一相位角θi均可布置在不同液缸对应的曲柄处.为方便标识,文中以相位角θi的排列顺序表示不同的布置方案,例如,方案(θ1,θ4,θ2,θ5,θ3)表示θ1,θ4,θ2,θ5,θ3布置在#1,#2,#3,#4,#5号缸对应曲柄位置.
五缸单作用往复泵曲轴曲柄具有5个不同初始相位角,故文中设计变量为5个初始相位角(θ1,θ2,θ3,θ4,θ5),相位值依次为0°,72°,144°,216°,288°.
1.3 目标函数
根据曲轴受力及强度分析,以曲轴危险截面j所受弯矩Mj最大值最小为优化目标,建立目标函数为minf(θ1,θ2,θ3,θ4,θ5)=maxMj.
2 SA算法
文中曲柄相位布置方案优化问题属于一般组合优化问题.模拟退火算法是一种求解组合最优化问题,达到求解全局优化问题的全局最优算法,克服了其他优化过程中容易陷入局部极小的缺陷和对初值的依赖性[14-15]等问题.
针对文中五缸单作用压裂泵曲轴曲柄相位布置方案优化问题,求解的模拟退火算法描述如下:
1) 解空间.解空间S可表示为所有初始相位角的循环排列组合,即S={(θ1,θ2,θ3,θ4,θ5)|θ1=0°,θ2=72°,θ3=144°,θ4=216°,θ5=288°},其中每一个循环排列表示曲柄相位的一种布置方案,初始解可选为(0°,72°,144°,216°,288°).
2) 目标函数.此时的目标函数为曲轴危险截面j所受弯矩Mj最大值最小或称代价函数.我们要求minf(θ1,θ2,θ3,θ4,θ5)=maxMj.
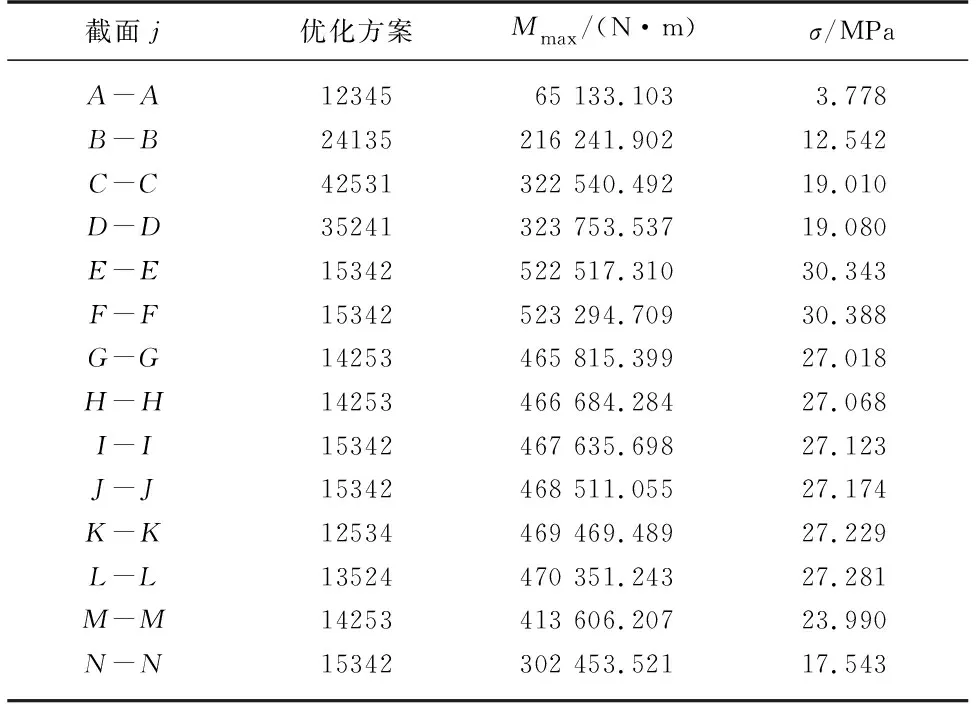
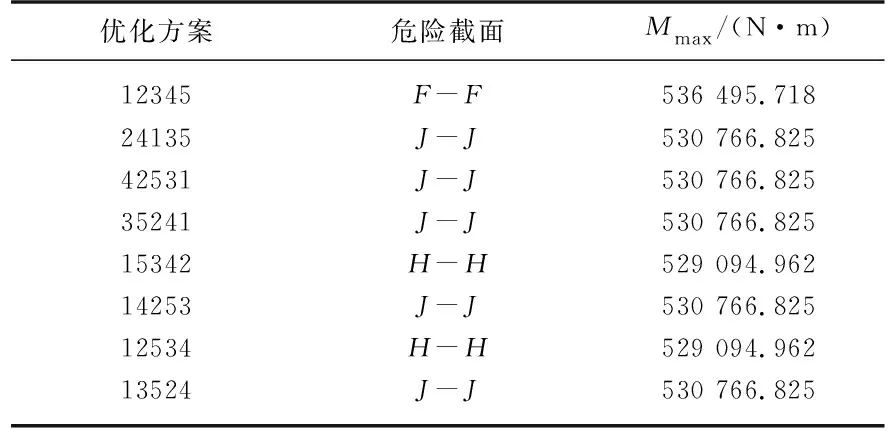
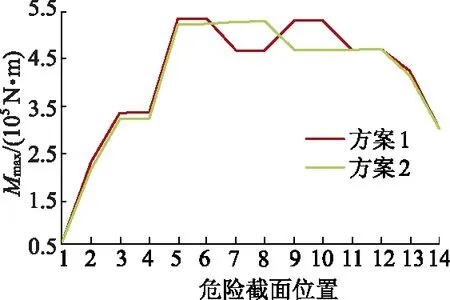
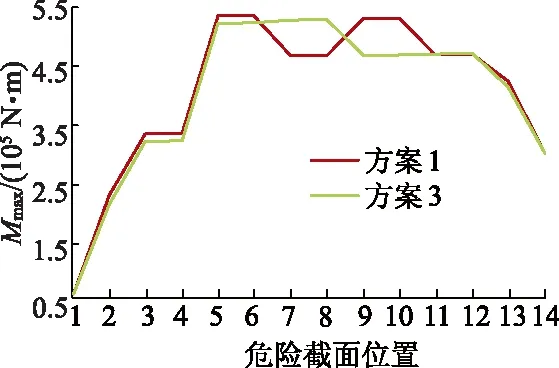
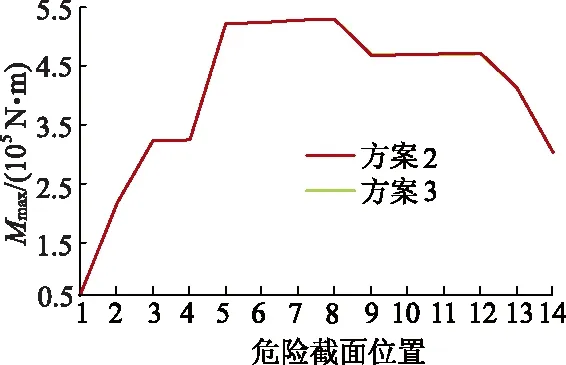
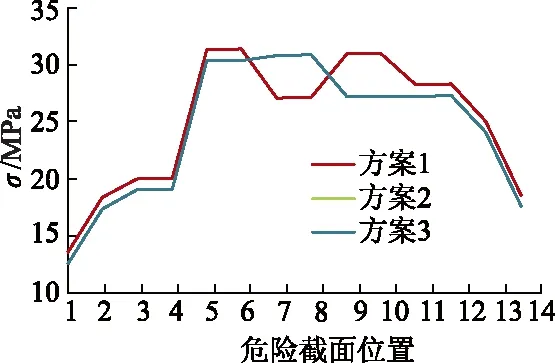
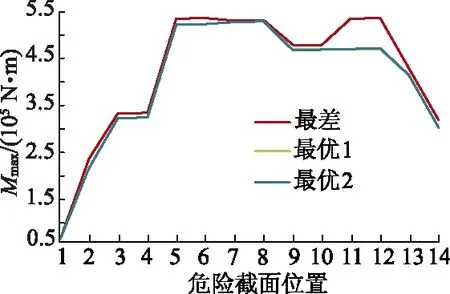
3) 新解的产生.文中由于设计变量数目较少,因此选用2变化法产生新解.任选序号m,n(m 4) 代价函数差.对于2变化法,危险截面j所受最大弯矩差可表示为Δf=maxMj(…,θn,…,θm,…)-maxMj(…,θn,…,θm,…). 5) 接收准则. 如果Δf<0,则接受新的布置方案.否则,按概率exp(-Δf/T)接受新的布置方案. 6) 降温.利用选定的降温系数K进行降温,即T←KT,得到新的温度,这里取K=0.999. 7) 结束条件.利用选定的终止温度e=10-30,判断退火过程是否结束.若T 以某型号往复泵为例,对其进行曲柄相位布置方案进行优化,其曲轴半径r=0.12 m,连杆长度l=0.86 m,曲轴转速n=150 r/min,泵压p=140 MPa,柱塞直径d=101.6 mm,斜齿轮半径r2=225.0 mm,压力角αn=20°,螺旋角β=16.26°. 文中五缸单作用往复泵曲轴总共有14个危险截面(A~N),目标函数为任一危险截面j所受最大弯矩的最小值,故优化方案仅为使危险截面j所受最大弯矩最小的优化方案,无法保证在此优化方案下,其他危险截面所受最大弯矩小于危险截面j所受最大弯矩,故需要对每个危险截面所受最大弯矩进行优化,这就需要改变目标函数所选危险截面j的位置进行14次优化求解. 以截面I-I为例,目标函数为minf(θ1,θ2,θ3,θ4,θ5)=maxMI,优化结束后,其适应度变化曲线如图7所示.优化结果为x=[0°,288°,144°,216°,72°],函数f(θ1,θ5,θ3,θ4,θ2)的最小值为467 635.698 3 N·m. 图7 适应度进化曲线Fig.7 Fitness evolution curve 选择不同危险截面j所得优化方案及所受最大弯矩最小值Mmax与弯扭组合应力σ如下表1所示,表中Mmax为最大弯矩,σ为弯扭组合应力. 表1 优化方案及所受最大弯矩最小值与组合应力Tab.1 Optimal arrangement and minimum values of maximum bending moment and combined stress 通过SA算法得到8种初步优化方案,每种方案下出现最大弯矩的危险截面及最大弯矩值如表2所示. 表2 危险截面及最大弯矩Tab.2 Critical sections and maximum bending moments 由表2可以看出,不同曲柄相位布置方案下,曲轴所受最大弯矩所在危险截面位置会发生改变,最大弯矩值也存在差异,考虑曲轴强度,各曲轴危险截面所受最大弯矩应越小越好,则方案12534和15342最优,即最优曲柄初相位布置方案为(θ1,θ2,θ5,θ3,θ4)和(θ1,θ5,θ3,θ4,θ2). 目前国内外五缸往复泵所采用的曲柄初相位布置方案主要以(θ1,θ3,θ5,θ2,θ4)为主,针对从120种方案中优选出的2种最优布置方案,进行曲轴受力及强度仿真分析.为便于区分目前五缸往复泵成熟产品所采用的曲柄相位布置方案及文中优选出的2种方案,定义方案1为(θ1,θ3,θ5,θ2,θ4),方案2为(θ1,θ2,θ5,θ3,θ4),方案3为(θ1,θ5,θ3,θ4,θ2). 方案1和2不同危险截面位置处最大弯矩值仿真对比分析如图8所示,图中横坐标1~14分别代表危险截面A~N. 图8 最大弯矩值Fig.8 Maximum bending moment 由图8可以看出,曲柄初相位布置方案1下,最大弯矩出现在危险截面J-J处,最大弯矩值为530 766.825 N·m,方案2下,最大弯矩出现在危险截面H-H处,最大弯矩值为529 094.962 N·m,方案2较方案1各危险截面最大弯矩值相对较小,个别危险截面最大弯矩值增大. 方案1和3不同危险截面位置处最大弯矩值仿真对比分析如图9所示,可以看出,方案3下,最大弯矩出现在危险截面H-H处,最大弯矩值为529 094.962 N·m. 图9 最大弯矩值Fig.9 Maximum bending moment 方案2和3不同危险截面位置处最大弯矩值对比分析如图10所示,可以看出,优选方案2和3不同危险截面位置处最大弯矩值曲线近似重合,最大弯矩值均为529 094.962 N·m,所在危险截面为同一截面H-H处.需要注意的是,由于相位布置方案的不同,在单个周期内,最大弯矩值出现的时刻并不一样. 图10 最大弯矩值Fig.10 Maximum bending moment 方案1,2,3不同危险截面位置处最大弯扭组合应力值对比分析如图11所示,可以看出,曲柄初相位布置方案2,3与方案1相比,最大弯矩所在危险截面的最大弯矩值降低;方案2,3不同危险截面位置处最大应力值曲线近似重合,且最大应力危险截面相同,均为H-H截面. 图11 最大弯扭组合应力值Fig.11 Maximum combined bending and torsion stress 最优布置方案下的危险截面为截面H,最差布置方案(θ4,θ5,θ1,θ2,θ3)下的危险截面为截面G.危险截面最大弯矩的对比结果如图12所示,可以看出,最优布置方案与最差布置方案相比,最大弯矩值减小约7 400 N·m,且危险截面L和M处最大弯矩值降低约12.3%. 图12 最大弯矩值Fig.12 Maximum bending moment 通过建立往复泵曲柄相位布置方案优化模型,基于模拟退火算法优化曲柄布置方案,对实际算例进行计算与分析,得到如下结论: 1) 建立了以曲轴曲柄初始相位角为设计变量,以曲轴危险截面所受最大弯矩值最小为目标函数的曲柄相位布置方案优化模型,该优化模型建立方法同样适用于多缸(五缸、七缸及九缸)单/双作用往复泵,具有通用性. 2) 应用模拟退火算法对往复泵曲柄相位布置方案进行了优化,结果表明模拟退火算法在解决该组合优化问题上收敛速度快、全局性好、鲁棒性强,并得到2种最优曲柄相位布置方案. 3) 对实际算例进行计算与分析可知,优化后的2种曲柄相位布置方案使得曲轴所受最大弯矩值及所受弯扭组合应力最小,最优布置方案与最差布置方案相比,最大弯矩值减小约7 400 N·m,且危险截面L和M处最大弯矩值降低约12.3%,有效改善了曲轴受力,进而有利于提高往复泵的工作性能.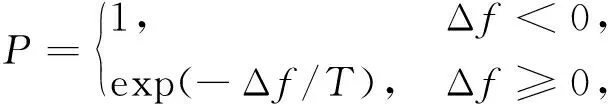
3 实际算例与分析
3.1 基本计算参数
3.2 优化结果

3.3 对比分析
4 结 论

