蜗壳断面面积变化规律对双吸离心泵水力性能的影响

赵万勇，陈帅*，赵强，李衍滨

(1. 兰州理工大学能源与动力工程学院，甘肃 兰州 730050；2. 兰州时昶水工机械有限公司，甘肃 兰州 730050)

双吸离心泵与单吸离心泵相比具有流量大、抗气蚀性能好等优点[1]，在供输水工程中应用广泛.某泵站使用2个厂家所生产的S700-500-730型双吸离心泵，泵运行参数相同，在同一泵组中，其中一厂生产的S700-500-730型双吸离心泵发生口环磨损、轴弯甚至断裂等故障，而另一泵厂生产的该型号双吸泵能够正常运转，从而对泵站的安全运行造成困扰.文中从S700-500-730型双吸离心泵断轴原因进行分析，对比2个厂家生产的泵结构、轴径以及运行工况没有明显的区别，初步分析某一厂生产的此型号双吸离心泵产生断轴故障的原因为该双吸离心泵在运行过程中产生过大的径向力所致[2].因此，文中以S700-500-730型双吸离心泵为研究对象，利用三维湍流数值模拟方法，探求不同蜗壳断面变化对径向力的影响.

陈元林等[3]研究认为，拥有良好水力特性的蜗壳应具备蜗壳断面面积在中前部较大、鼻端处适当放大、中后部渐渐收缩的基本特征.汤远等[4]分析了断面面积线性变化与符合二次多项式的非线性变化2种蜗壳形式对离心泵水力性能的影响，认为在不同工况下，改进的设计方案能够有效地提高离心泵水力效率以及降低蜗壳内水力损失.BELBACHIR等[5]通过对比基础设计与附加设计的3种蜗壳，对比分析了三者的水力特性、叶轮周向速度分布以及压力分布，表明蜗壳设计对泵的水力性能影响显著.高波等[6]通过非定常数值计算，分析了4 种蜗壳断面面积变化规律对离心泵水力性能的影响，结果表明蜗壳面积变化规律在设计工况下对离心泵水力性能的影响较小，而在非设计工况下差异较大，同时蜗壳断面设计规律变化能够引起叶轮周围静压分布变化，致使叶轮所受径向力的大小发生改变.

目前，针对蜗壳断面面积设计规律的研究主要集中在单级单吸离心泵，而对双吸离心泵的流动特性、水力性能以及双吸泵在运行过程中所受径向力的影响则鲜有研究.因此，文中从泵蜗壳的断面面积变化规律着手，在不改变叶轮和吸水室设计参数的基础上，分析蜗壳断面面积变化规律对双吸离心泵水力性能及径向力的影响，从而为解决由于径向力过大而导致的断轴问题提供一定的理论依据.

1 几何模型

S700-500-730型双吸离心泵是一种单级双吸中开蜗壳式离心泵，其主要设计性能参数分别为流量Qd=1.125 m3/s，扬程H=39.3 m，转速n=740 r/min，比转数ns=183.叶轮及蜗壳主要几何参数如图1所示，分别为叶轮进口直径Dj=463.0 mm，叶轮出口直径D2=757.9 mm，叶轮出口宽度b2=137.8 mm，叶片数Z=6，蜗壳基圆直径D3=757.9 mm，蜗壳进口宽度b3=188.7 mm．叶轮叶片的进口边以及出口边做圆角半径为R=2.0 mm的圆角处理，模型中其他棱角进行半径为R=5.0～8.0 mm的圆角处理.并规定在笛卡尔坐标系中，叶轮旋转方向为Z轴正方向，液流从出口延长段流出的方向为X轴的正方向.

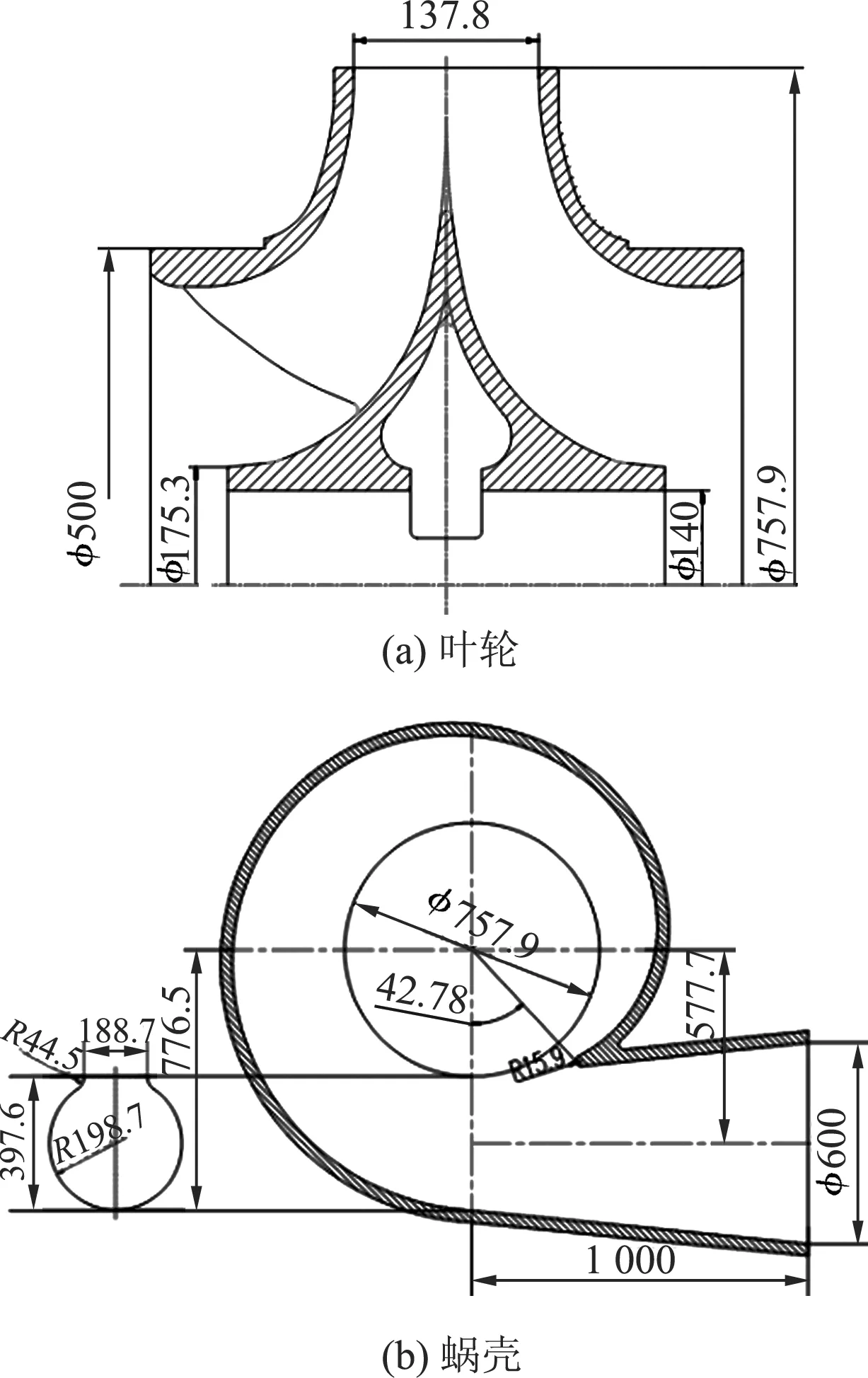
图1 几何形状和主要尺寸参数Fig.1 Geometrical shape and primary dimensions

以厂方提供的蜗壳数据得到第一组面积变化规律(简称Y-规律型)与依据速度系数法[7]所得到的传统设计规律(简称L-规律型)对比如图2所示.通过参考相关设计规范，依据离心泵比转数ns=183选取速度系数K3=0.343，通过计算发现该厂所设计的第360°断面的面积要大于采用传统设计规律所设计的第360°断面的面积，并且传统设计规律的蜗壳断面面积呈线性变化，而该泵的蜗壳断面面积呈近似“S”变化.

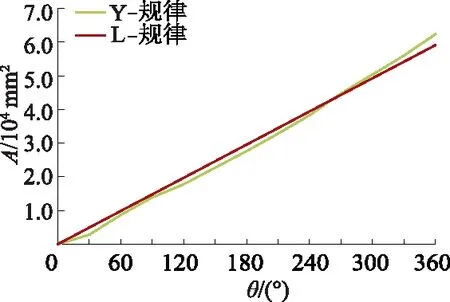
图2 Y-规律与L-规律设计蜗壳断面面积对比Fig.2 Comparison of section area between Y-law and L-law

2 数值计算

2.1 计算模型及网格划分

应用三维建模软件对2种方案的蜗壳以及相配的叶轮和吸水室的水体部分进行三维建模，最终求解域的装配结果如图3所示.

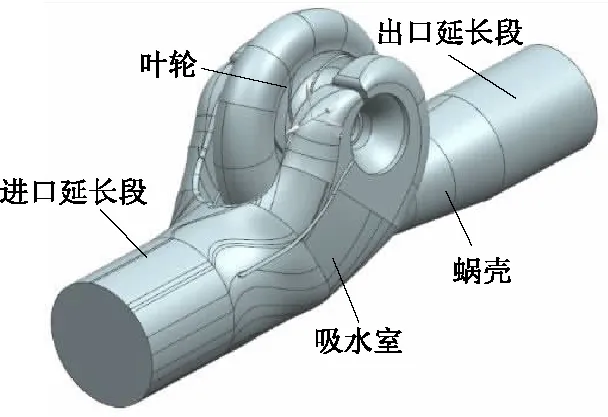
图3 计算模型Fig.3 Computational fluid domain model

对叶轮、吸水室以及蜗壳等的水体采用四面体非结构化网格及八叉树[8]划分方法，同时对叶轮与蜗壳的交界面、吸水室与叶轮的交界面以及蜗壳的隔舌等部分进行局部加密.装配体网格及各部件网格如图4所示，经检验，网格质量≥0.3，满足计算要求.

图4 网格示意图Fig.4 Grid patterns

在清水工况下，以扬程H及水力效率ηh为标准，对采用Y-规律设计方案的双吸离心泵进行网格无关性验证[9]，结果如图5所示.当网格数N大于1 000 万时，计算结果相差无几，符合网格无关性要求.

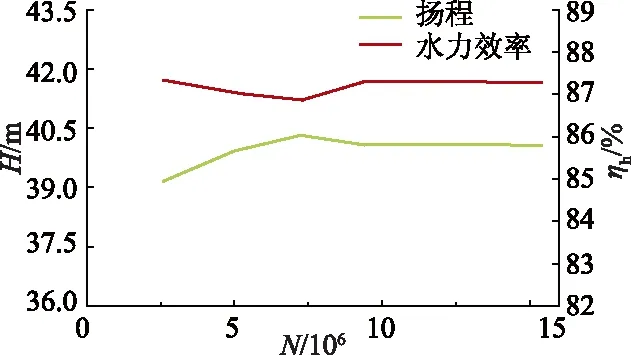
图5 网格的无关性验证Fig.5 Grid independency validation

文中选用网格数为9 383 649的网格模型进行计算，同时保证2种方案的网格划分方法一致，最终各装配体的网格数如表1所示.

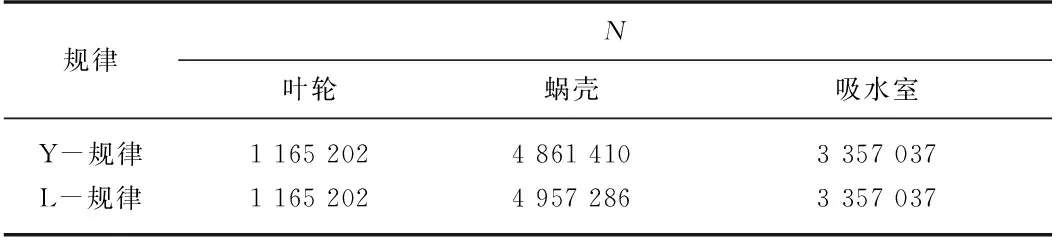
表1 计算网格数Tab.1 Number of mesh cells

定常计算时，流体介质选择清水，湍流模型采用较广泛的标准k-ε模型.边界条件按照双吸泵叶轮水体为旋转域和其余流体域为静止域设置.进口边界条件为速度进口，出口边界条件采用自由出流以及固定无滑移壁面条件.

进行非定常计算时，以设计工况下的定常计算结果作为流场初始条件.时间步长设为Δt=0. 675 ms，即叶轮每旋转3°计算1步.为了方便对比分析，每隔30°取一蜗壳截面，如图6所示.

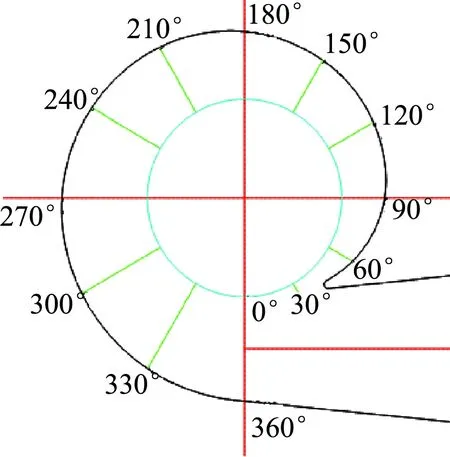
图6 截面设置Fig.6 Cross-section set-up

2.2 数值计算方法验证

数值计算方法的正确性不仅和网格的数量有关，而且还与近壁区的网格质量有关，文献[10]给出了无边界层以及粗、细3种边界层网格的Y+值范围.此次选取无边界层进行计算，由表2可知，湍流模型选用标准k-ε模型时，各部件的Y+值在要求范围内.

表2 近壁区网格Y+值范围Tab.2 Y+ values of mesh near wall

图7为在清水工况下不同流量工况时，双吸离心泵外特性曲线的计算值和试验值对比.可以看出，当忽略机械损失、摩擦等外界因素时，二者的误差在4%以内，由此可以说明该数值计算方法是正确的.

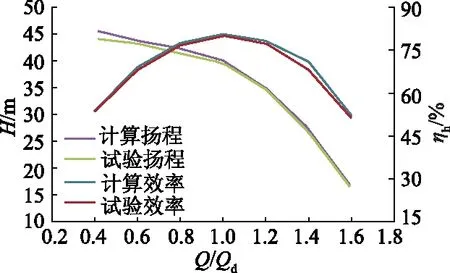
图7 不同工况下离心泵的外特性曲线Fig.7 Experimental and predicted performance curves of centrifugal pump

3 计算结果及分析

3.1 外特性对比分析

为研究蜗壳断面面积变化规律对双吸离心泵水力性能的影响，在不同工况下对2种方案进行定常计算，得到2种方案时泵的外特性曲线，如图8所示.

图8 泵外特性曲线Fig.8 Predicted performance curves of two pumps with Y-law and L-law profiles

由图8可知，数值计算和试验的外特性曲线变化趋势基本一致，扬程随流量的增大而减小，效率随流量的增大呈先增大后减小的趋势，并且在设计工况下效率均达到最大值.

为了探究2种蜗壳断面面积规律方案对双吸离心泵水力性能的影响，引入扬程相对变化ΔH以及效率相对变化Δη，即

(1)

(2)

式中：HY为采用Y-规律的扬程值；HL为采用L-规律的扬程值；ηY为采用Y-规律时效率值；ηL为采用L-规律时效率值.

表3为在不同工况时计算得到的扬程相对变化ΔH以及效率相对变化Δη，可以看出：在设计工况下，采用2种规律的双吸离心泵水力性能相近；在非设计工况下，对于采用Y-规律的蜗壳，其扬程值基本较L-规律的蜗壳高，其中在工况0.6Qd，1.1Qd，1.2Qd处表现最为明显，其扬程值相对增加量分别为 0.56%，0.72%，1.55%；就双吸泵效率而言，采用Y-规律的蜗壳，其效率值基本较L-规律的蜗壳高，其中在工况0.4Qd，0.8Qd，1.2Qd处表现最为明显，其效率值相对增加量分别为 1.74%，0.93%，1.27%.

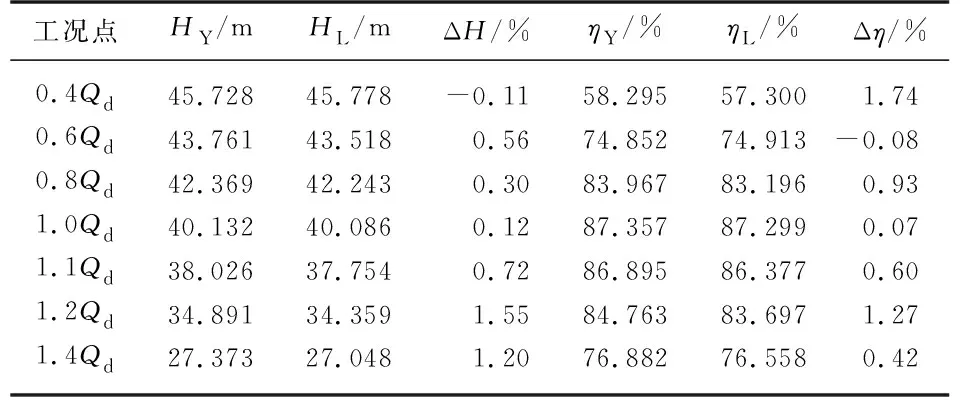
表3 不同工况下采用2种规律泵的扬程及效率参数Tab.3 Head and efficiency of two pumps with Y-law and L-law profiles

由此可以认为，采用Y-规律的蜗壳能够明显的提升双吸泵的扬程及效率，尤其是在大流量工况下运行，提升效果更为明显，这也是厂家采用该规律设计蜗壳断面的主要原因.

3.2 速度场对比分析

在设计工况下，采用2种规律泵蜗壳90°，180°，270°，360°断面上的流速分布如图9所示，可以看出：在90°～270°断面，采用不同规律的断面速度分布相似，宏观上各断面内主流两侧的速度分布基本对称；在270°～360°断面的流道区间内，Y-规律的断面流速分布较L-规律断面的分布更加均匀，对称性表现更加明显.速度分布的对称性越高则流体在蜗壳流动时产生的流动损失越小[11]，这即是S700-500-730型双吸离心泵在设计工况下采用Y-规律方案比采用L-规律方案扬程高0.12%和效率高0.07%的原因.

图9 不同规律方案时蜗壳不同截面绝对速度分布对比Fig.9 Comparison of velocity contours in volute cross-sections

3.3 压力场对比分析

蜗壳与旋转部件的配合影响流体在蜗壳内的流动情况以及双吸离心泵的水力特性[12].设计工况下，2种规律蜗壳中心截面的压力分布如图10所示.

图10 设计工况下2种蜗壳中心截面压力云图Fig.10 Pressure contours in volute mid-span plane under design conditions for two pumps

由图10可以看出：2种蜗壳中心截面的压力分布总趋势大体一致.一般而言，蜗壳内压力分布越均匀、压力梯度越小则流体流动的均匀性越高，其水力损失越小.在60°～270°截面区间内，Y-规律截面面积较L-规律的截面面积降低了6%～15%.在此区间，采用Y-规律的压力梯度要明显低于采用L-规律的压力梯度，同时采用Y-规律的蜗壳压力分布及过渡的均匀性要高于采用L-规律的蜗壳.在270°～360°截面区间内，Y-规律截面面积较L-规律的截面面积提高了0.90%～5.49%，但是2种方案在此区间的压力梯度相差不大.

3.4 定常径向力对比分析

改变蜗壳断面面积规律能够影响蜗壳各个断面的速度分布以及叶轮出口处绝对速度的大小和方向，使得叶轮中流体与蜗壳中流体相遇时的能量转换发生改变，从而引起叶轮周围静压分布变化，导致作用在叶轮上的径向力发生改变[13].通过对该双吸离心泵的速度场和压力场进行分析可以发现：在小流量工况下，蜗壳中的速度自隔舌处开始逐渐减小，压力逐渐增大，由压力引起的径向力FY的方向大约与隔舌成90°，同时由动反力引起的径向力FX的方向大约指向隔舌，且大约与径向力FY成90°；在大流量工况下，作用在叶轮上的径向力FX和FY的方向与小流量工况下相反，总径向力F的方向可由二者的正切值求得.

图11为不同流量下，2种蜗壳的径向力分布及总径向力.

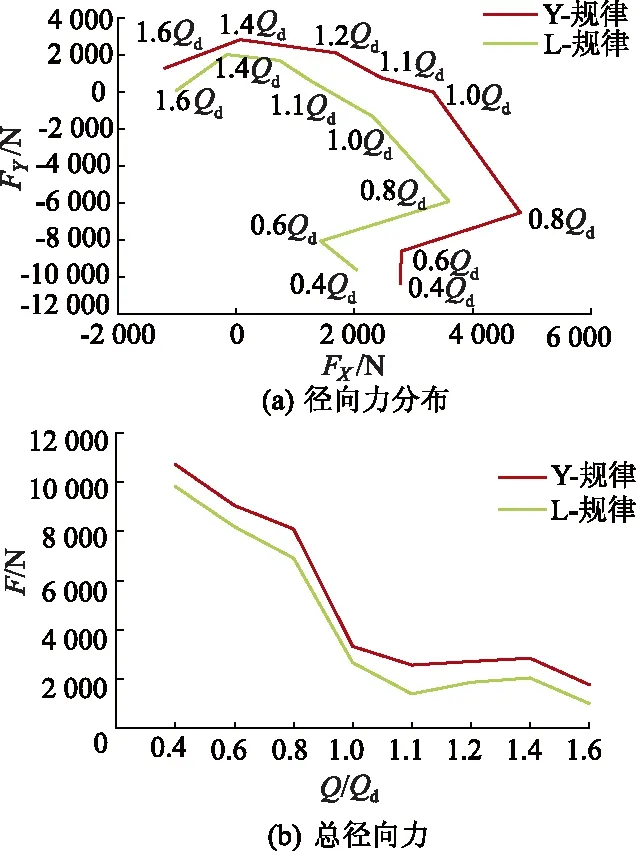
图11 不同流量下2种蜗壳时泵的径向力分布及总径向力曲线Fig.11 Radial force components and total force at various flow rates for two pumps

由图11a可以看出：2种蜗壳设计方案作用在叶轮上的径向力分布类似，径向力的方向随流量的改变而产生变化；采用L-规律设计的蜗壳能够有效地改善在不同工况下作用在叶轮上径向力的分布情况，从而增大双吸泵在不同工况下运行时的稳定性.由图11b可以看出：在工况为1.1Qd时，作用在叶轮上的径向力最小，这与理论上双吸泵在设计工况点附近运行时所产生的径向力最小相符合[14].

为对比分析2种规律时对叶轮所受径向力的影响，计算了径向力的相对增加量ΔF，如表4所示.

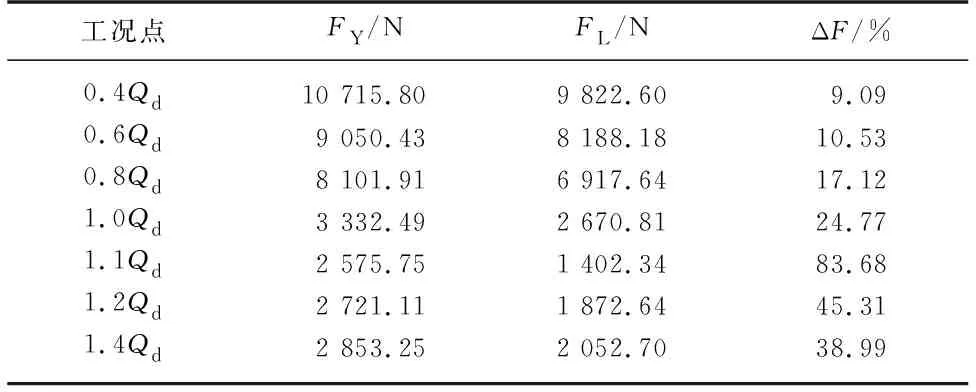
表4 不同工况下2种规律泵的径向力Tab.4 Radial force of two pumps under different conditions

(3)

式中：FY为Y-规律的双吸离心泵径向力值；FL为采用L-规律设计的双吸离心泵径向力值.

由表4可以看出：相较于传统设计规律，Y-规律的蜗壳在设计工况下径向力相对增加量达到24.77%；相较于传统方法设计的蜗壳，在工况为0.8Qd下径向力的相对增加量为17.12%，在工况为1.2Qd下径向力的相对增加量为45.31%.由此可知，采用L-规律设计的蜗壳比采用Y-规律设计的蜗壳更能有效降低作用在叶轮上的径向力，双吸离心泵运行时稳定性也更好.

3.5 非定常径向力对比分析

图12为叶轮旋转第6周时作用在叶轮上的径向合力随时间的变化曲线，可以看出：叶轮所受径向力呈现周期性的脉动；Y-规律的脉动幅值要明显高于L-规律的脉动幅值，这说明采用Y-规律的双吸离心泵在运行时会更容易造成叶轮振动，从而使得双吸离心泵运行不稳定.

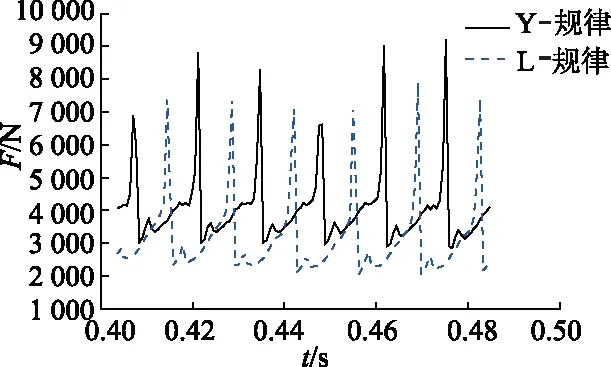
图12 叶轮径向力时域图Fig.12 Impeller radial force in time domain

对图12进行快速傅里叶变换[15]，得到如图13所示的设计工况下叶轮所受径向力脉动幅值δF频域特性图.由图13可知，2种方案的径向力脉动幅值都呈逐渐降低的趋势，Y-规律和L-规律中的径向力脉动主频均在叶片通过频率(74 Hz)处，采用Y-规律方案设计的蜗壳结构的高频脉动比采用L-规律方案设计的蜗壳结构的高频脉动更明显.这说明采用L-规律方案设计的蜗壳结构能够明显降低作用在叶轮上的径向力脉动，从而降低叶轮发生振动的可能性，使得泵运行更加稳定.

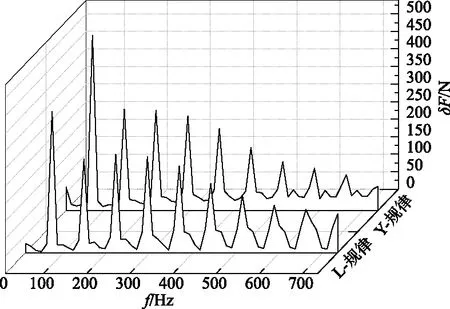
图13 叶轮径向力脉动幅值频域图Fig.13 Impeller radial force pulsation amplitude in frequency domain

通过对2种方案进行定常径向力及非定常径向力对比分析，可以发现，蜗壳的断面面积变化规律对双吸离心泵运行过程中所产生的径向力影响比较明显，而作用在叶轮上的径向力直接影响着双吸离心泵在运行过程中的稳定性.因此，泵站S700-500-730型双吸离心泵出现叶轮口环磨损、轴弯以及断轴等故障的原因是采用了Y-规律方案进行蜗壳结构的设计.

4 结 论

以某厂生产的S700-500-730型单级双吸式离心泵为研究对象，针对不同蜗壳断面面积规律对离心泵水力性能对比以及降低径向力性能进行分析，得到结论如下：

1) 2种规律的双吸离心泵在设计工况下水力性能相近. 在非设计工况下,相比传统设计方案，该厂所采用Y-规律蜗壳能够明显提高双吸离心泵的扬程及效率.

2) 通过对2种方案进行定常径向力及非定常径向力对比分析，发现蜗壳断面面积变化规律对作用在叶轮上的径向力影响显著，Y-规律的蜗壳的相对增加量要高于L-规律的蜗壳的相对增加量.同时，Y-规律的脉动幅值以及高频脉动都比采用L-规律方案设计的蜗壳结构时脉动幅值以及高频脉动更明显.这大大地增加了泵在运行时旋转轴所承受的交变载荷，从而使得双吸离心泵在运行过程中发生口环磨损、轴弯甚至断轴故障.