利用数学情境 加强问题提出 促进深度学习

吴小燕 项祖法

摘    要：问题提出在数学学习中占有重要的地位，有效的数学情境是学生提出数学问题的基础.利用数学情境实施问题提出教学，既为学生提供了更好的学习机会，又促进了学生深度学习.

关键词：数学情境;问题提出教学;深度学习

问题提出在数学学习中占有重要的地位，正如爱因斯坦所言：“提出一个好问题往往比解决一个问题更重要”.问题提出可以给学生提供更多的学习机会，从而培养他们的应用意识与创新意识.近两年来，我们在长江学者、美国特拉华大学教授蔡金法团队的引领下，对中小学数学问题提出教学进行了重点研究.蔡金法就数学问题提出的定义作了这样的说明：数学问题提出是指基于某个问题情境，通过接受已知或改变已知的方式来发现新的数学问题，然后将其以问题的形式表达出来[1] . 因此，有效的数学情境是学生提出数学问题的基础.我们针对不同内容的不同需求，在通过任务驱动型、操作实践型、变式教学型、质疑问难型数学情境，加强问题提出与解决、促进学生深度学习的教学实践与研究中，收获了一些成果.

一、利用任务驱动型情境激发学生的探究欲望

义务教育数学课程标准强调要加强生活与数学的联系.在浙教版教材九年级上册第三章“圆”第二课时的教学实践中，我们从身边的现象入手，创设了任务驱动型的情境，把学生原有认知基础与当前情境背景下的问题有效结合起来.

学习该内容之前，学生已经理解确定圆心与半径，就可以画出圆，在此基础上，还认识了弦、圆弧.而当前教学目标之一是经历不在同一直线上的三个点确定一个圆的探索过程，了解不在同一直线上的三个点确定一个圆.为此，我们创设了如下情境：

王奶奶有一个心爱的手镯，不小心打碎了（如图1），这是其中最长的一段.王奶奶非常想再定制一个一样大小的手镯.你能根据此图想到并提出一些跟圆有关的数学问题，帮王奶奶了却愿望吗？

面对这样一个现实问题，学生非常愿意用自己所学的知识一展身手（约定破损的手镯看成是一段圆弧）.在学习过程中，我们看到学生提出许多与圆有关的数学问题，归纳如下：

问题1： 可以根据圆的一部分画出整个圆吗？

问题2： 一个圆中的任意一段圆弧是否可以通过旋转或拼凑形成一个圆？

问题3： 怎么找到这段圆弧所在圆的圆心？

问题4： 这段圆弧的半径怎样确定？

问题5： 是不是所有的破损圆都可以恢复原形？

问题6： 这段破损的圆弧周长是多少？能求出所在圆的面积吗？

针对学生提出的问题，教师引领学生探究讨论，并转化成利用这段圆弧来找出圆心和半径，操作中学生提出如下问题：

问题7： 经过两个已知点（比如圆弧的两个端点）能画几个圆？

问题8： 经过圆弧上三个点，能画出几个圆？

问题9： 经过圆弧上四个点，能画出几个圆？

问题10：经过圆弧上至少几个点就可以找出圆心，画出圆？

在这样的任务驱动情境下，促进了学生有条理地进行数学思考和表达，使学生的学习不断得到深入与发展.

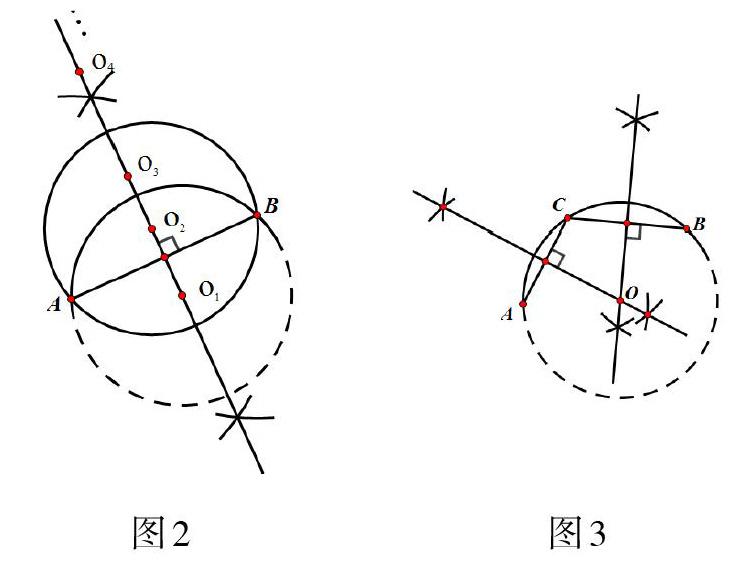
在教学实践中，我们注意到任务驱动型的数学情境创设，需顺应学生的年龄特征与生活实际，通过激发学生内心的主动性来实现提出问题与解决问题.在圆弧上取一点探圆心，到圆弧上取两点探圆心（如图2），到圆弧上取三个点确定圆心（如图3）的过程中，学生充分体会到探究这类问题的方法與数学思想，学会运用数学思维来思考当前数学情境，促进学生深度思考，培养学生数学素养.

二、利用操作实践型情境形成学生的方法迁移

动手操作是探究数学知识、获得活动经验的重要形式，不同学生的操作结果可能不一样，但这为同伴互助探究提供丰富的素材，能引发更多数学问题的提出，有效促进学生学习的深入.图形的折叠是几何中最常见的一种轴对称变换，折叠问题可以综合特殊三角形、四边形等知识，把方程思想、分类思想等思想方法蕴含其中.

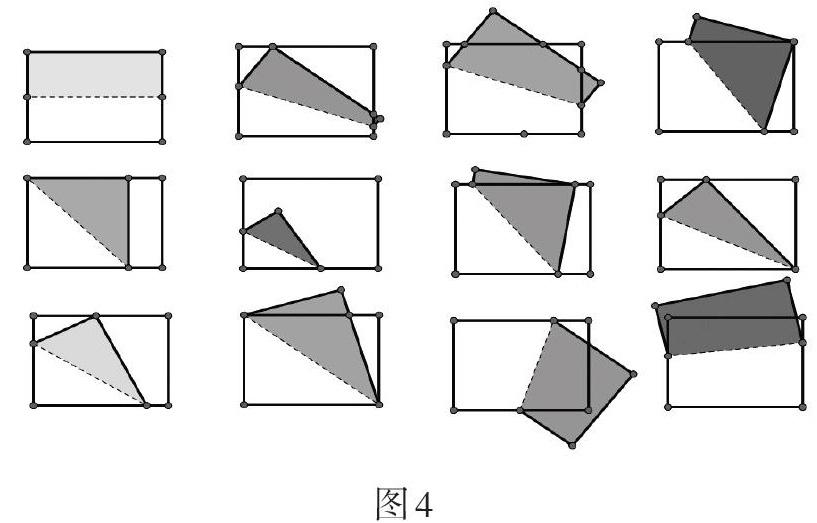
有一张长为20cm，宽为12cm的矩形纸片，请将矩形纸片ABCD折叠一次;观察你所折叠的图形，并思考可以研究怎样的数学问题（先个人操作思考，后小组合作讨论）.

折叠情况如图4所示.

小组提出的问题主要有：

问题1：折叠后发现多种情况看似因为折叠方式的不同，其实就是折痕位置的不同，当选定某一种方式时，我们要问，折痕位置在哪里？线段的长又是多少？

问题2：不同的折叠情况下都产生重叠面积，重叠面积分别是多少？

问题3：求面积的关键其实就是求相关线段的长度，我们怎样求得折痕长度和一些相关线段的长度呢？

问题4：这么多的折叠情况，我们选择哪几个图形来研究比较好？

有学生回答，应该先解决一类特殊的折叠，就是通过折叠使得点B落在边AD上（如图5）.

创设动手操作的数学情境，能为问题提出提供可以触摸的、现实的学习素材.学生在经历操作、观察、抽象、运算等学习过程，考虑问题更加深入，从而提升数学的思考力.一般学生通过对这些操作素材的观察，可以提出一些基础性的问题，从而增进他们的学习机会;基础较好的学生在简单问题的基础上能提出更有深度的问题，引发一题多解，并由特殊解法向一般解法推广，从而促进学习方法的迁移.

操作实践型情境给学生提供一个亲身体验的过程，使课程内容的呈现更显层次性和多样性，能让更多的学生有表达自己想法的机会.教师充分利用这些操作素材，及时抓住提问机会，不断刺激学生形成新的想法和问题，可以将学习活动推向更深、更广的层次.

三、利用变式教学型情境提升学生知识建构能力

知识体系的建构能促进知识的理解与掌握.问题提出教学中，学生提出的问题具有层次性与发展性，对知识链接起到极大的推动作用.在“三角形专题复习”的教学实践中，我们以基础问题为知识建构型情境，在解决问题和知识重构的基础上，引导生成新的问题（如变式问题）和学习内容.

（一）基础问题

已知在△ABC中，AB=3，AC=5，BC=6，请提出通过计算求值的数学问题.

学生根据以前所学的三角形的高线、中线与角平分线等内容，集中提出以下问题：

问题1：三角形的面积是多少？

问题2：三角形的高线是多长？

问题3：三角形的中线、角平分线又各是多少？

这些问题涉及面积、高、中线、角平分线， 由于考虑到部分问题的解决方法类似，就统一选取BC边上的高、BC边上的中线及∠A的平分线长来解答.学生通过分析看到这些量之间的关系，抓住核心问题，顺藤摸瓜，顺利地解决了这些问题.下面是我们在教学中学生求高线、中线与角平分线的解答过程.

求高线：在△ABC中，AB=3，AC=5，BC=6，求BC边上高线AD的长（如图6）.

[32-x2=52-（6-x）2]  [x=53]  AD=[2314]

求中线：在△ABC中，AB=3，AC=5，BC=6，求BC边上中线AH的长.

解：[AH=AD2+DH2=22].

求角平分线：在△ABC中，AB=3，AC=5，BC=6，求∠BAC平分线AF的长（如图7）.

解：[BFCF=S△ABFS△AFC=ABAC=35].[BF=38BC=94].

[AF=AD2+DF2=1054].

（二）变式问题

已知在△ABC中，AB=3，AC=5，请提出相关的数学问题.

前面已经计算了三角形的中线、高线与角平分线，顺此思路，学生自然想到长度，但不能计算具体的值，那么它们的范围是否可以探究？于是有学生进一步提出：

问题1：BC边上高线的最佳范围是什么？

问题2：BC边上中线的取值范围是什么？

问题3：∠A平分线的取值范围是什么？

问题1比较简单，学生画图后口答解决，问题2、问题3的解答如下：

变式一：△ABC中，AB=3，AC=5，求BC边上中线AH 的取值范围.

解法1：倍长中线（如图8）.

解法2：中位线（如图9）.

在△ACE中   AC-CE<2AH

1

在△AFH中  AF-FH

1

變式二：△ABC中，AB=3，AC=5，求∠A平分线AF的取值范围（如图10）.

解：[BFCF=ABCE=35].在△ACE中，[AC-CE<8k

0

在教学活动中，问题提出与问题解决是一个有机的整体.因此，问题情境的创设需同时考虑两者的需要，既要有利于学生提出问题，又要有利于学生再次利用情境和素材解决问题，充分发挥问题情境的多重作用.本案例在设置基础问题之上，巧妙变式求高线、中线、角平分线的范围，这样，使学生保持思考过程的连贯性，促进了学习的深化.此外，利用兼顾问题提出与解决的情境，有助于学生形成完整的解决问题的思路，经历完整的解决问题的过程，对于发展学生的应用意识与实践能力也能起到较大的推动作用.

四、利用质疑问难型情境完善学生数学认知结构

数学学习是一个不断完善的过程，在学习过程中，只有勇于挑战困难，才能不断弥补短板，形成更加完整的知识体系.在教学过程中，很多学生对于有难度的问题会采取回避的态度，不敢主动请教老师或同学.在八年级上册第五章“一元一次不等式”的学习中，教师发现学生对“在含有两个字母的一次不等式中，明确了未知数的取值，求含参量字母的取值范围”这类题型存在解法上的困难，其原因是不等式中的两个字母干扰学生的思维，造成认知障碍和理解困难.教师有针对性地选择素材，由学生来编题，再引导学生自行解决，改变学习方式，将主动权交还给学生，促使他们发现错因并纠正错误.教学过程中，我们通过以下情境，引导学生提出问题：

对于不等式[a-2x>-2]，请同学们添加一个条件，提出一个思维含量较高的数学问题考考大家.

在这一情境下，学生提出的问题充分展现其尚未掌握的“疑难杂症”.这些问题按照难易程度排列如下：

问题1：当a<2，求x的解集.

问题2：[x<22-a] ，求a的取值范围.

问题3：x<4，求a的值.

问题4：不等式的正整数解为1，2，3，求a的取值范围.

问题5： 不等式有4个负整数解，求a的取值范围.

在解答这些问题的过程中，学生逐步归纳出解系数含参的一元一次不等式的一般步骤：在系数化为1时，先判断系数的正负情况，从而根据不等式的性质求出解集;将不等式中的字母看作常数，解出不等式的解集，将解出的解集和已知条件相对应，确定大致范围（利用数轴确定不等式的解集），验证端点值（对范围的端点进行代入验证）.

这些问题都是平时易错的题型，用“考考大家”的方式让学生给同伴提出问题，更能满足学生的表现欲，释放其思维中的纠结点，同时也将学生的错误或困惑有效转化为一种宝贵教学资源，成为提升学生深度学习能力的一服良药.

质疑问难型情境的创设，能再次激发学生的认知冲突，通过学生提出问题、解决问题来完善原有的认知结构，从中反省自身的学习习惯，提升数学核心素养.这样的情境创设素材需要教师平时悉心观察，敏锐地捕捉学生的易错点，及时标记或记载，并进行分析与归类.

参考文献：

[1]蔡金法.数学问题提出的例子、类型和内涵[J].小学数学教师，2019（7/8）：34-40.