圆锥曲线中非对称代数式的处理方法

施利强 江战明

摘    要：2019年浙江省高考数学卷圆锥曲线题的处理过程中，出现不能直接用韦达定理处理的非对称代数式.对于该问题，教师可借助对称式[y1+y2，y1y2，y1-y2，y1y2+y2y1]，化非对称代数式为对称式[y1=12（y1+y2+y1-y2）]，[y2=12[（y1+y2）-y1-y2]].从而将任意的非对称代数式[my1+ny2]化为对称式[my1+ny2=λ（y1+y2）+μy1-y2）]，最终可以用韦达定理解决.

关键词：高考;圆锥曲线;非对称代数式

2019年浙江省高考数学卷圆锥曲线题的处理过程中，出现不能直接用韦达定理处理的非对称代数式.笔者开设了一堂关于圆锥曲线中非对称代数式处理的公开课，对该问题进行了探讨.笔者考虑到圆锥曲线题型的代数运算量和课堂的可操作性，本堂课围绕一个椭圆模型展开.

一、非对称问题的引入

（一）课堂引入，模型建立

在课堂的引入部分，针对2019年高考的圆锥曲线题，笔者给出两个探究问题，让学生一起探究.

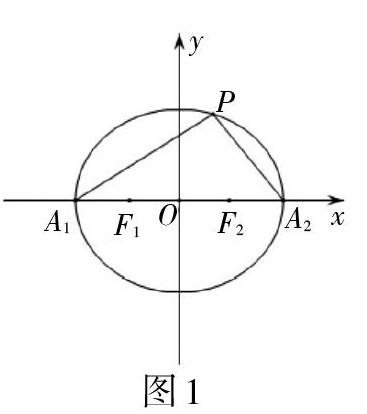
探究一：如图1，已知点[P]为椭圆[x24+y23=1]上一个动点，问：[kPA1kPA2]是否为定值？

解析：A1（-2，0），A2（2，0）设[P（x0，y0）]，[kPA1kPA2=y0x0+2?y0x0-2=y20x20-4]，由[P（x0，y0）]在椭圆上即[x204+y203=1]，代入消元化简得：[kPA1kPA2=-34].

【评注】学生的证明过程用到点在曲线上这个条件，这也是我们处理圆锥曲线参数问题的常用消元方法.

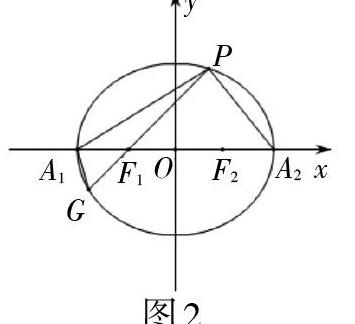
探究二：如图2，过点[P]与左焦点[F1]作焦点弦[PG]，并连接[A1G]，问：[kPA1kGA1]是否为定值？

解析：设[lPG：x=my-1].与椭圆方程联立： [（4+3m2）y2-6my-9=0]，得到：

[y1+y2=6m4+3m2y1y2=-94+3m2]，同时算得：

[x1+x2=-84+3m2x1x2=4-12m24+3m2].当然，化简的过程用到[x1=my1-1，x2=my2-1]，即点在直线上消元.最后得出结论：[kPA1kGA1=y1y2（x1+2）（x2+2）=-94]，是一个定值.

其中，代入直线消元也是我们处理圆锥曲线参数问题的常用方法.

问题：结合刚才探究一的结论：[kPA1kPA2=-34]，是否可以得到[kPA2，kGA1]之间的关系？

解答：两个式子作除法，可以得到：[kPA2kGA1=13]，即斜率的比值是一个定值.

【评注】通过这两个探究，让学生回顾在解决圆锥曲线问题时常用的两种处理方法：点代入曲线消元和代入直线消元.另一方面，在回顾旧知识的同时，引出本节课主要的椭圆模型，并得到模型中斜率的比值的定值关系，为下文引出本节课的主题做好铺垫.

（二）深入探究，引发冲突

引入部分借助于已知的常用结论，得到[kPA2，kGA1]之间满足的关系式[kPA2kGA1=13]，如果直接探究，是否也可以顺利得到该关系式？

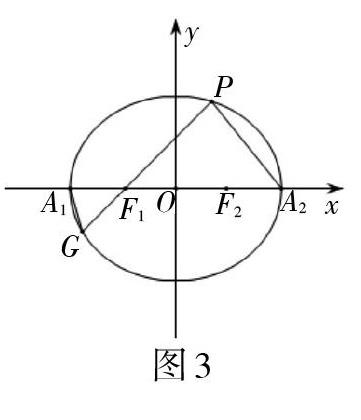
问题重述：如图3，过点[P]与左焦点[F1]作焦点弦[PG]，连接[PA2]，[A1G]，问：[kPA2kGA1]是否为定值？

解析：设[P（x1，y1），G（x2，y2）]， [kPA2kGA1=y1y2?x2+2x1-2]，再由点在直线上[x1=my1-1，x2=my2-1]，消元得到：[kPA2kGA1=y1y2?x2+2x1-2=y1y2?my2+1my1-3=my1y2+y1my1y2-3y2].

一般能用韦达定理解决的代数结构式是对称式：[y1+y2，y1y2，y1-y2，y1y2+y2y1].此时我们发现，这里的目标式是非对称代数式，不能很顺利地由韦达定理解决.但是由前两个探究我们可以知道，代数式的结果是一个定值[13].具体如何求？

【评注】深入探究，通过点代入直线消元化简代数式，发现目标式不能用韦达定理直接解决，从而引发冲突.同时，由于代数结构的非对称，提出非對称代数式，并强调能用韦达定理解决的对称式：[y1+y2，y1y2，y1-y2，y1y2+y2y1].

二、非对称问题解决方法探究

方法1：化非对称式为对称式

我们知道常用对称式有：[y1+y2，y1y2，y1-y2，y1y2+y2y1]，如果还是想要化非对称代数式为对称式，是否可以将目标式转化为这些对称式，从而利用韦达定理解决.比如最简单的非对称式[y1]，是否可行？

解析： 假设[y1>y2]，就得到对称式：[y1=12（y1+y2+y1-y2）].同理可以得到关于[y2]的对称式：[y2=12[（y1+y2）-y1-y2]].

由本题图形的对称性，以下我们都假设[y1>y2].此时，对于任意关于[y1，y2]的线性结构：[my1+ny2]，代入[y1，y2]的对称式或者利用待定系数法，都可以得到对称式：[my1+ny2=λ（y1+y2）+μy1-y2）].这样任意的非对称代数式都可以化成对称式，最终利用韦达定理化简求解.

回到原问题：[kPA2kGA1=my1y2+y1my1y2-3y2]，假设[y1>y2]，利用[y1，y2]的对称代数式，[y1=12（y1+y2+y1-y2）]，[y2=12[（y1+y2）-y1-y2]]，[y1-y2=121+m23m2+4]分别得到：[my1y2+y1=14+3m2[-6m+61+m2]]，[my1y2-3y2=14+3m2[-18m+181+m2]]，则[kPA2kGA1=my1y2+y1my1y2-3y2=13]，并将学生的结果投屏.

【评注】借助对称式[y1+y2，y1y2，y1-y2，]

[y1y2+y2y1]，化非对称代数式为对称式：[y1=12（y1+y2+y1-y2）]，[y2=12[（y1+y2）-y1-y2]].从而可以将任意的非对称代数式[my1+ny2]化为对称式[my1+ny2=λ（y1+y2）+μy1-y2）]，最终可以用韦达定理解决.另一方面，这里化非对称代数式为对称代数式，将分子、分母都化成以[m]為主元的代数式，所以选定主变元也很重要.

方法2：利用点在曲线上化对称

方法1消元的时候利用的是点在直线上消元，是较常用的消元方法.本题由于代数式结构的特殊性，还可以利用点在曲线上消元，从而达到化对称的目的.由于该方法的特殊性，直接给学生作演示.

解析：[k1k2=y1y2?x2+2x1-2]，两边平方得：[k21k22=y21y22?（x2+2）2（x1-2）2]，由于[x214+y213=1]，[x224+y223=1]，消去[y1，y2]，并化简得：[k21k22=1-x2141-x224?（x2+2）2（x1-2）2]

[=（4-x21）（4-x22）?（x2+2）2（x1-2）2]

[k21k22=（x1+2）（x1-2）?（x2+2）（x2-2）=]

[x1x2+2（x1+x2）+4x1x2-2（x1+x2）+4][=19]，结合图象可得，[k1k2=13].

【评注】利用点在曲线上消元，一方面与课前的复习内容相呼应.另一方面，将非对称代数结构化为对称式，从而可以用韦达定理解决.进而说明化非对称式为对称式方法的多样性，也为突出方法1的优势做铺垫.

三、变式训练   感受方法

通过刚才的探究，学生已经学到几种处理非对称问题的方法，相对来说，学生觉得方法1利用[y1=12（y1+y2+y1-y2）]，[y2=12[（y1+y2）-y1-y2]]化非对称式为对称式实用一点.作为该方法的巩固，接下来在原来椭圆模型的基础上提出以下变式训练，并选取部分学生的结果进行投屏探讨.

变式1：如图4，已知椭圆[x24+y23=1]，[AB]为过左焦点[F1]的焦点弦，点[A]在[x]轴上方，求[2F1A+1F1B]的取值范围.

解析：[F1A=1+m2y1]，[F1B=1+m2y2]，

[2F1A+1F1B=11+m2（2y1+1y2）][=11+m2（2y1-1y2）=11+m22y2-y1y1y2][=2-13m1+m2 ][∈53，73].

【评注】在前面模型的基础上做变式训练，让学生进一步了解用该方法在解决非对称问题时要注意的地方.并在训练中让学生慢慢掌握这种处理非对称问题的方法，体会该方法在处理非对称问题时的优势.

变式2：如图5，已知椭圆[x24+y23=1]，[AB]为过左焦点[F1]的焦点弦，点[A]在[x]轴上方，求[2F1A+F1B]的取值范围.

解析1：[2F1A+F1B][=1+m2（2y1-y2）]，

[2y1-y2=12（y1+y2）+32（y1-y2） ，][2F1A+F1B=1+m2?3m-181+m24+3m2].

解析2：由椭圆极坐标公式：[F1A=ep1-ecosθ]，[F1B=ep1+ecosθ]

（其中[e=12]，[p]为焦准距，[p=b2c=3]）

[1F1A+1F1B=2ep][=43].其中[F1A∈（a-c，a+c）=（1，3）]

[2F1A+F1B][=34?（2F1A+F1B）?（1F1A+1F1B）][=34?（3+F1BF1A+2F1AF1B）]

令：[F1AF1B=t]，[t∈13，3]，则[2F1A+F1B=34（3+1t+2t）∈][94+322，7]

【评注】从变式2也可以看到，本题目标式也是非对称式，但今天的方法也不一定是万能的，解析1虽然能将目标式用主变量[m]表示，但是结果也不一定容易计算，这时候需要选取合适的方法来解决，解析2利用极坐标公式顺利地解决了该问题.当然该类化非对称式为对称式题型的核心还是统一变量，不同的题化对称式选取的主变量可能也会不同.

四、拓展延伸   巩固提高

最后给出基于本节课模型的几个思考题，希望学生能对该类非对称式题型的处理方法有更进一步的感悟.

例题：已知椭圆[x24+y23=1]，点[P]为椭圆上的一个动点，[A1，A2]分别为左右顶点.

思考题1：如图6，[PG]为过左焦点[F1]的焦点弦，分别过P，[A2]与G，[A1] 作直线[PA2]，[GA1]交于点[T]，证明：点[T]落在定直线上.

思考题2：如图7，点[Q（m，0）]是椭圆长轴上异于左右焦点的定点，连接[PQ]并延长交椭圆于点[G]，分别过P，[A2]与G，[A1] 作直线[PA2]，[GA1]交于点[T]，证明点[T]的横坐标为定值.

思考题3：如图8，点[Q（m，0）]是椭圆长轴外的定点，连接[PQ]交椭圆于点[G]，分别过P，[A1]与G，[A2] 作直线[PA1]，[GA2]交于点[T]，证明点[T]的横坐标为定值.

【评注】本节课的最后，为了让学生能进一步体会并掌握该处理方法，提出本课模型下的三个思考题，从而达到拓展学生的思维、巩固旧知识、提高学生能力的作用.

五、总结升华   感悟提升

本堂课笔者以一个椭圆模型贯穿始末，由我们的常见结论引出椭圆中的非对称式的问题，在复习旧知的同时引出非对称式的问题.通过层层引导，得出解决该类问题的主要方法是化非对称式为对称式，并强调转化过程中得注意主变量的选取，最终利用韦达定理得以解决.当然解决该类问题的方法很多，通过练习也发现该方法并不是万能的，得看具体情况选取解决方法.最后提出的三个思考题也是非对称式问题，其背景是极点极线理论，是否以该理论为背景的题较多会出现非对称目标式有待我们进一步挖掘.另外，双曲线和抛物线中也有类似的非对称式问题，针对不同圆锥曲线类型，是否还有其他处理方法，有待我们进一步探究.