函数图形的应用问题
◇ 李京林
函数图形的应用在各级各类考试中出现的频率越来越高,内容可以涉及方方面面.解题的关键是正确理解函数图象的变化规律,利用函数图象特征、性质对实际问题进行综合分析.下面结合几类常见函数图象的应用问题加以实例剖析.
1 实际问题中抽象函数图象的分析
例1在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线y=f(x),一种是平均价格曲线y=g(x)(如f(2)=3表示开始交易后第2小时的即时价格为3元;g(2)=4表示开始交易后2个小时内所有成交股票的平均价格为4元).下面所给出的4个图象中,实线表示y=f(x),虚线表示y=g(x),其中可能正确的是( ).
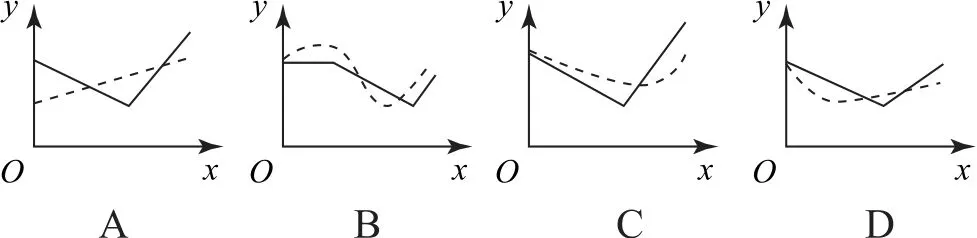
刚开始交易时,即时价格和平均价格相等,排除选项A;开始交易后,平均价格应该跟随即时价格变化,在任何时刻其变化幅度应该小于即时价格变化幅度,排除选项B和D.故选C.
在解决与现实生活相关的函数图象问题时,往往通过实际问题在不同情况下所具有的特征,结合函数图象的变化特征加以分析与判断.
2 运动问题中函数图象的判断题
例2如图1,点P在边长为1的正方形ABCD上运动,设点M是CD边的中点,当点P沿A→B→C→M运动时,点P经过的路程记为x,△APM的面积为y,则y=f(x)的图象可能是( ).
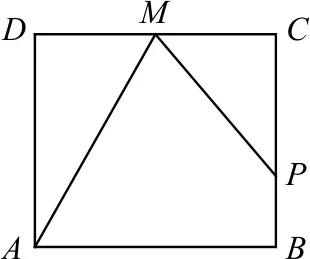
图1
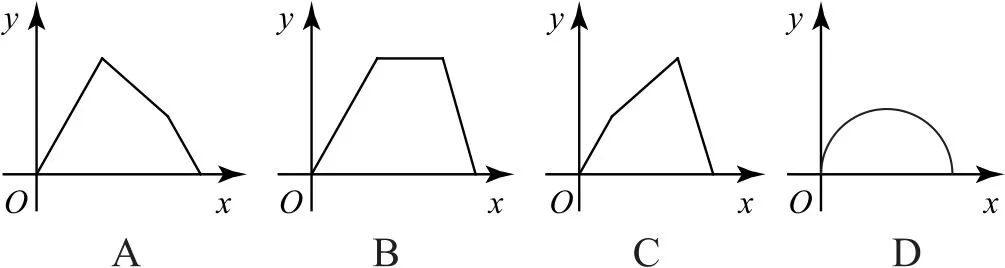
当点P从A到B运动时,△APM的面积y直线上升,达到最大值;当点P从B到C运动时,△APM的面积y逐渐减小.根据对应的图形,只有A满足条件,故选A.
对于运动性函数图象问题,通过实际函数图象考查分段函数问题,学会在实际情境中理解函数关系,并综合实际问题与数学问题之间的关系加以分析有关的图象问题.
3 函数图形与函数性质的交会与综合问题
例3图2到图4展示了一个由区间(0,1)到实数集R的映射过程:区间(0,1)中的实数m对应数轴上的点M,如图2;将线段AB围成一个圆,使两端点A,B恰好重合,如图3;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),如图4.图4中直线AM与x轴交于N(n,0),则m的象就是n,即记作f(m)=n.
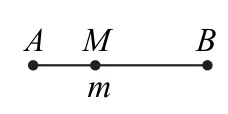
图2
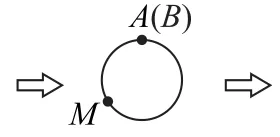
图3
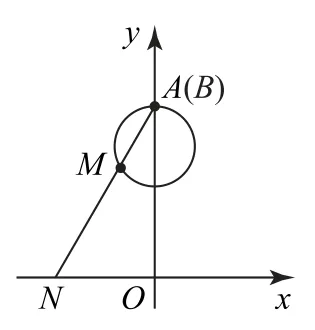
图4
①f(0.25)=1;②f(x)是奇函数;③f(x)在定义域上单调递增;④f(x)的图象关于点(0.5,0)对称.由图4可知,当m<0.5时,f(m)<0,故①不正确;由于0<x<1,f(x)的定义域不关于原点对称,所以f(x)不是奇函数,故②不正确;当点M由点A运动到点B时,点N的运动方式是从-∞运动到+∞,f(x)为增函数;当m=0.5时,f(m)=0,由图象知道其是对称的,即f(x)的图象关于点(0.5,0)对称.故填③④.
实际应用中,往往给出一个函数图象,通过函数图象所表达出来的性质确定函数的相关性质,这也是高考中经常涉及的一类有关函数图象的题型,要正确加以分析与应用.

