具有状态反馈的异质多智能体系统的群组均方一致性

李 晓，孟欠欠，胡贺军，孙 贺

淮北师范大学计算机科学与技术学院，安徽淮北，235000

多智能体系统是由一组相互作用的智能体构成，并能完成单个智能体所不能完成的复杂而精确的任务[1]。多智能体系统的协同控制在无人机、机器人、电力系统、智能交通系统等若干领域都有着潜在的应用[2-4]。作为协同控制的关键问题，一致性问题的研究更是受到学者的广泛青睐。一致性问题可描述为各智能体通过自身信息传递和局部信息融合，使得整个多智能体系统的状态(位置、速度、加速度等)趋于一致。为获取多智能体系统一致性的充分条件，大部分的研究要求智能体间的拓扑结构具有生成树。然而，由于外界环境的影响，很难实现智能体的整个拓扑结构具有生成树，但部分智能体间的拓扑结构具有生成树却相对容易满足。因此，近年来关于多智能体系统的群组一致性受到了广泛关注。群组一致性是指多智能体系统的拓扑结构由多个部分智能体组成的子图构成且每个子图都具有生成树，通过设计控制协议，使得不同群组多智能体系统在组内达到某种状态的一致性。多智能体系统的群组一致性在分布式传感网络、军事侦察系统以及危险品检测等应用中发挥重要作用。

近年来，通过分析一致性以及群组一致性条件，对多智能体系统进行的研究涌现了丰硕的成果。YU等[5]考虑了在切换拓扑结构下多智能体系统满足群组一致性的充分条件。宋海裕等[6]研究了一类在牵引控制下的多智能体系统群组一致性问题。纪良浩等[7]分析了一类低阶时延多智能体系统在无向拓扑结构下的存在分组时的一致性条件。Ma等[8]研究了一类二阶非线性多智能体系统跟随领导者的群组一致性问题。杨繁[9]提出了多智能体系统分别在有向拓扑图和无向拓扑图的群均衡化算法。林瑜阳等[10]研究了一类二阶连续多智能体系统的在分组情况下的一致性。程玉娟等[11]给出了一类非线性多智能体系统在切换拓扑网络结构下导致的分组一致性条件。王伟等[12]通过设计基于智能体记忆状态的快速一致性协议，研究了一类低阶多智能体系统在有向拓扑结构下的快速分组一致性问题。司马嘉欢[13]考虑了一类在固定有向拓扑网络下的高阶多智能体系统分组一致性的充要条件。然而，以上文献都是基于同阶多智能体组成的系统。在智能体系统的实际工程应用中，一方面，不管是自然界个体或者人造工程系统，在功能上或者在结构上其差异都是不可避免的，因此动力学完全一致的智能体难以获取。另一方面，由于群体间智能体的通信以及执行能力存在着差异性，难以用统一的动力学模型去描述智能体的耦合关系，因此，关于异质多智能体系统实现一致性的条件分析具有更大的理论价值和应用前景。鉴于此，本文设计了有效的控制协议，并给出了一类由低阶和高阶智能体构成的异质多智能体系统在均方意义下的群组一致性条件，最后，利用数值算例对获得的结果进行了验证。

1 预备知识和问题描述

1.1 预备知识

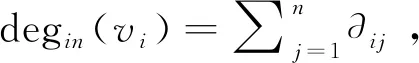
1.2 问题描述

考虑一类由n个一阶智能体和m个二阶智能体组成的异质多智能体系统，系统模型描述如下：

(1)

(2)

而Μ1={1,2,…,n},Μ2={n+1,n+2,…,n+m}，χi(t)∈Rm1,νi(t)∈Rm2,μi(t)∈Rm3分别表示位置、速度以及控制输入。

本研究的异质多智能体系统群组均方一致性问题可以总结为：给定异质多智能体系统(1)(2)，设计控制协议μi(t)使得系统渐近地实现群组均方一致性。即设计控制协议μi(t)

可以使得智能体状态满足如下：

limΞ{|χi(t)-χj(t)|2}=0,∀i,j∈Μ1∪Μ2

limΞ{|νi(t)-νj(t)|2}=0,∀i,j∈Μ2

(3)

其中,Ξ表示期望。

2 控制协议设计

设计状态反馈控制协议(4)如下：

(4)

∀i∈Μ2

(5)

其中,N1i={vj∈M1|(vj,vi)∈E}，N2i={vj∈M2|(vj,vi)∈E},Κ1,Κ2,Κ3为待求解的控制增益。

定义

分别将控制协议(4)(5)代入系统(1)(2)得到如下闭环系统：

(6)

其中

针对以上矩阵l1,l2中的元素作出以下假设:

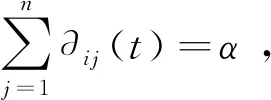
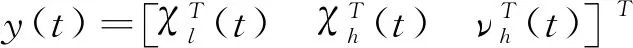
系统(6)可以写成如下矩阵形式:

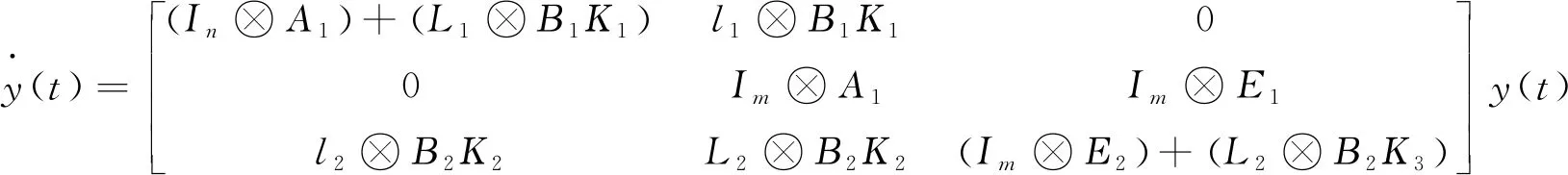
(7)

随后，对系统(7)进行如下模型变换。令

ξli(t)=χ1(t)-χi(t),i∈{2,3,…,n}

ξhj(t)=χn+1(t)-χj(t),ζhj=νn+1(t)-νj(t),j∈{n+2,n+3,…,n+m}

φ(t)=[ξTl2(t)…ξTln(t)ξTh(n+2)(t)…

易得

(8)

其中

ψ=diag{ψ1ψ2ψ3},ψ1=[1n-1-In-1]⊗Im1

ψ2=[1m-1-Im-1]⊗Im1,ψ3=[1m-1-Im-1]⊗Im2

定义如下可逆矩阵

(9)

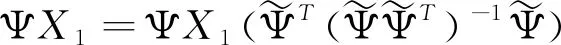
根据(9)式以及L11n=0,L21m=0，可以得到:

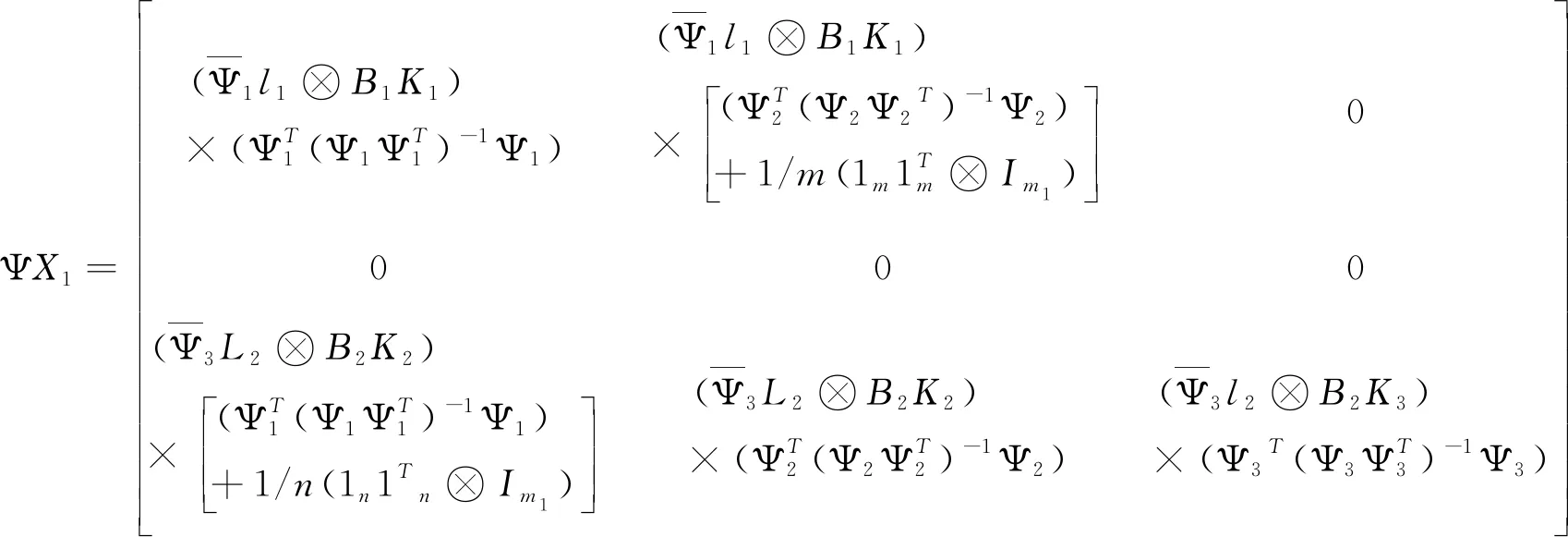
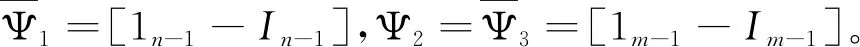
由假设可知:l11m=-α1n,l21n=-β1m

Ψ1(1n⊗Im1)=0,Ψ2(1m⊗Im1)=0

(10)

成立，可以得到:

随后易得:

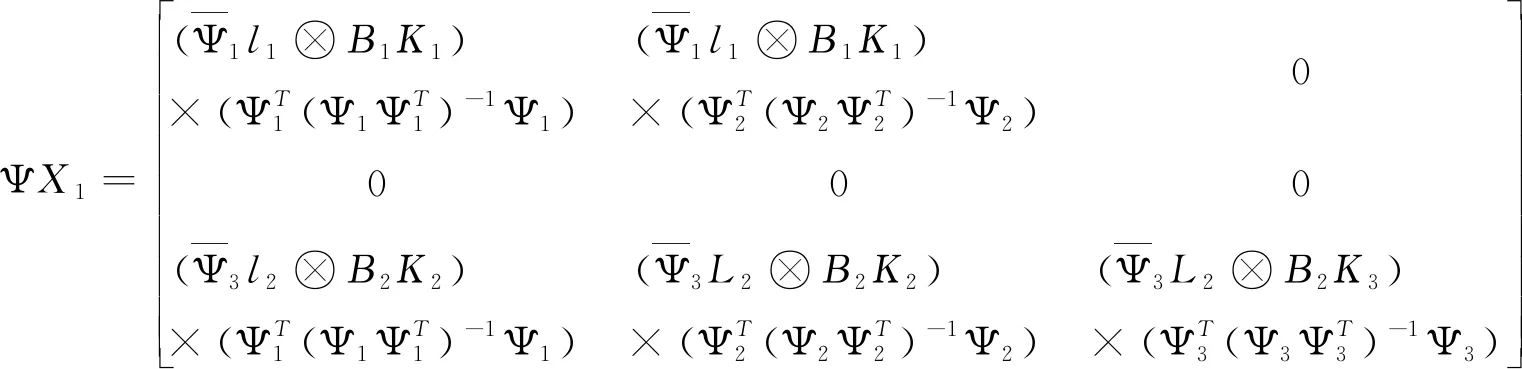
即

同理可得:

根据矩阵性质可得:

结合式(10)可得:

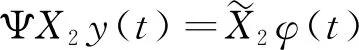
综上得到如下降阶闭环系统:

(11)

其中

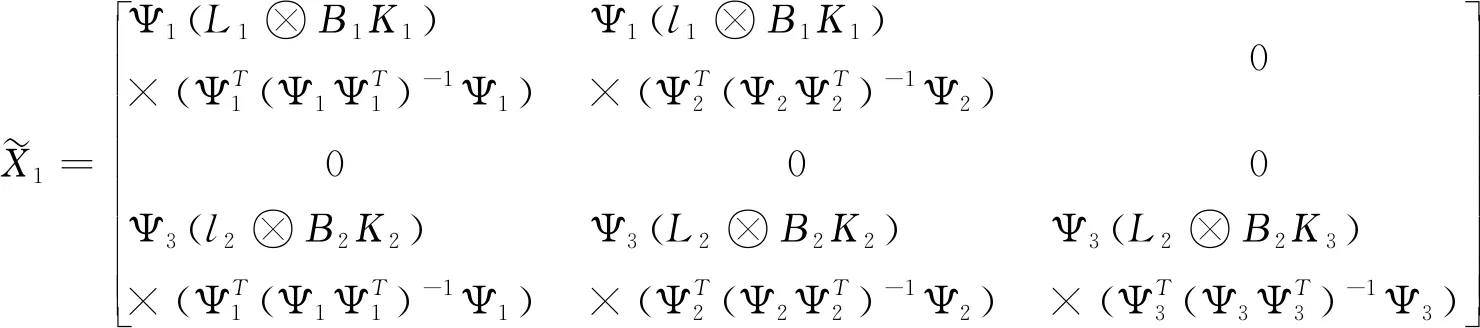
(12)

(13)

上述利用矩阵理论、图论以及一系列等价变换，将待研究的异质多智能体系统(1)(2)满足群组一致性的条件转换成分析闭环系统(11)满足渐近均方稳定性的充分条件。在后续内容中，结合Lyapunov稳定性理论，以定理的方式给出在有向拓扑结构下系统(11)满足渐近均方稳定性的分析条件以及系统(1)(2)满足渐近均方一致性的综合结果。

3 分析与综合

定理1假设一阶以及二阶多智能的有向拓扑图G1，G2具有有向生成树。如果存在正定阵P，使得下式：

(14)

成立，其中

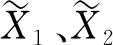
证明:构造如下Lyapunov函数：

则V(t)沿着系统(11)的轨迹为:

根据Lyapunov稳定性理论可知系统(11)是渐近均方稳定的当下式

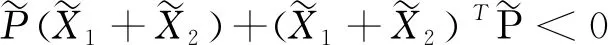
(15)

成立，即式(14)成立。证毕。

定理2假设一阶以及二阶多智能的有向拓扑图G1，G2具有有向生成树。若存在正定矩阵Ω以及矩阵Y1,Y2,Y3使得下面的线性矩阵不等式:

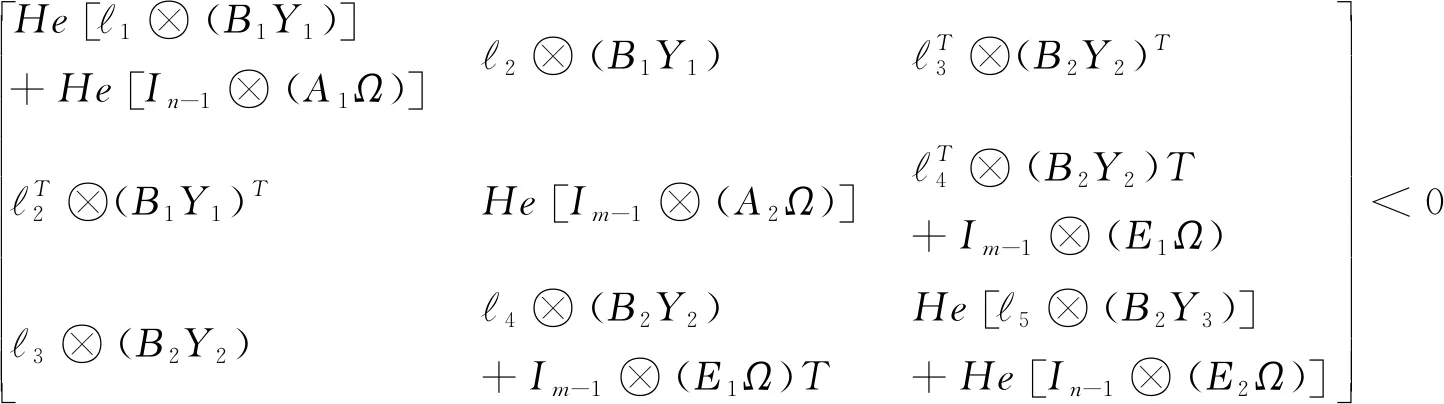
(16)

成立，其中

则系统(1)(2)满足群组均方一致性，控制增益如下：

Κ1=Y1Ω-1,Κ2=Y2Ω-1,Κ31=Y3Ω-1

(17)

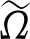
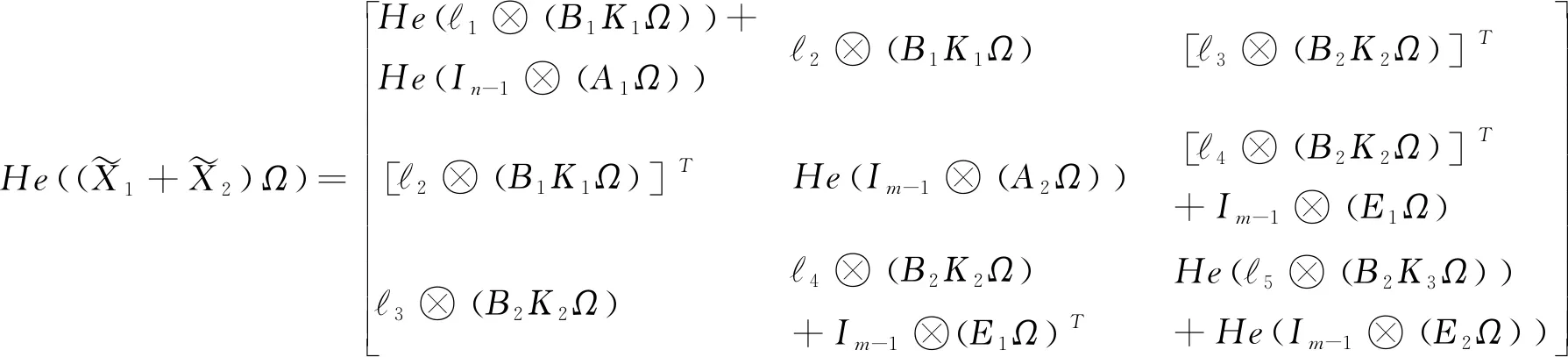
(18)

根据(17)式可得式(18)等价于式(16)。证毕。

4 数值算例

考虑由6个智能构成的异质多智能体系统，其中智能体1-4满足一阶动力模型，5,6满足二阶动力学模型，系统描述如下：

其拓扑结构包含两个子图G1，G2，如图1所示。

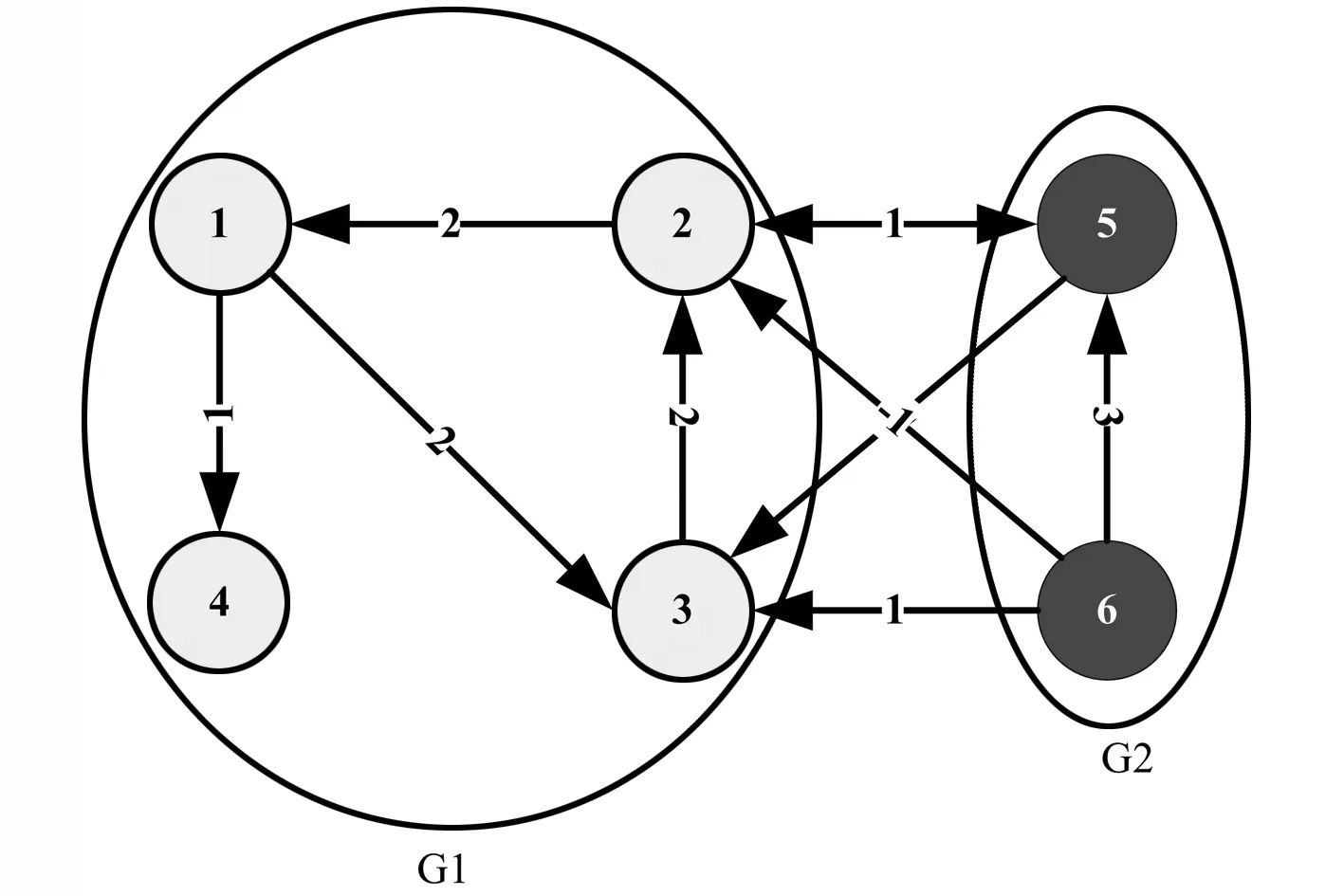
图1 6个智能体间有向拓扑图

G1，G2均具有有向生成树，G1和G2以及两个子图之间对应的Laplace矩阵分别为:

将以上参数代入定理1的(14)式中，通过Matlab获得可行性解以及相应的控制增益:

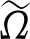
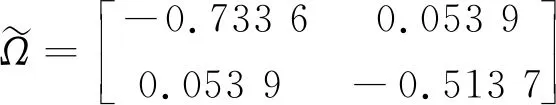
可得，所研究的一类多智能体系统(1)(2)在控制协议(4)(5)作用下能够实现群组均方一致性。

5 结 语

通过设计状态反馈控制协议研究了一类由一阶和二阶多智能体构成的异质多智能体系统在均方条件下满足群组一致性的充分条件。随后，对系统模型进行变换，进而将异质多智能体系统群组一致性问题转换为低阶闭环系统的渐近稳定性问题。利用图论、矩阵理论以及Lyapunov稳定性定理给出了闭环系统渐近均方稳定以及多智能体系统群组均方一致性的充分条件。最后，通过数值算例对结果的正确性进行了验证。